Journal of Mathematical Finance
Vol. 2 No. 4 (2012) , Article ID: 24462 , 11 pages DOI:10.4236/jmf.2012.24031
The Malliavin Derivative and Application to Pricing and Hedging a European Exchange Option
Division of Actuarial Science, School of Management Studies, University of Cape Town, Cape Town, South Africa
Email: sure.mataramvura@uct.ac.za
Received August 29, 2012; revised October 2, 2012; accepted October 14, 2012
Keywords: Exchange option; contingent claim; hedging; generalized CHO formula
ABSTRACT
The exchange option was introduced by Margrabe in [1] and its price was explicitly computed therein, albeit with some small variations to the models considered here. After that important introduction of an option to exchange one commodity for another, a lot more work has been devoted to variations of exchange options with attention focusing mainly on pricing but not hedging. In this paper, we demonstrate the efficiency of the Malliavin derivative in computing both the price and hedging portfolio of an exchange option. For that to happen, we first give a preview of white noise analysis and theory of distributions.
1. Introduction
White noise analysis and theory of distributions is treated extensively in [2-5] and references therein. Applications in the form of the generalized Clark-Haussmann-Ocone (CHO) formula was studied in [6-8] and references therein. The theorem takes advantage of the martingale representation theorem which expresses every square integrable martingale as a sum of a previsible process and an Itô integral. The power of the generalized CHO is that one can take advantage of the Malliavin derivative for computing the hedging portfolio. The Malliavin derivative is a better mathematical operation as opposed to the delta hedging approach whose limitations are a failure to explain differentiation of some payoffs which are not differentiable everywhere or if the underlying security is not Markovian. Most of the attention in contingent claim analysis is directed at pricing because of its importance to market practitioners. It is in this regard that explicit results of hedging portfolios for different options are not always readily available. In this paper, we present both explicit results of the price and hedging portfolio of an exchange option, written on two underlying securities with independent Brownian motions. The ground-breaking work was done in [1]. The market setup is a complete market setup to escape the problem of not finding a perfect hedge.
Hedging portfolios are just as important as prices of options in that they give us an understanding of how sellers or writers can managed dynamically to replicate the payoff of a contingent claim. The price at any time of the contingent claim equals the intrinsic value of the hedging portfolio at that point.In the case of a European exchange option, the payoff  is the difference in terminal value of the underlying securities, conditional on the buyer’s terminal asset price
is the difference in terminal value of the underlying securities, conditional on the buyer’s terminal asset price  being more than the seller’s,
being more than the seller’s, . A more interesting problem will be to look at an American exchange option where the buyer would exercise on or before maturity. Such an exercise time will be a stopping time and the price for such an option will be the essential supremum, over all stopping times, of the payoff above. Our attention in this paper is on the European exchange option.
. A more interesting problem will be to look at an American exchange option where the buyer would exercise on or before maturity. Such an exercise time will be a stopping time and the price for such an option will be the essential supremum, over all stopping times, of the payoff above. Our attention in this paper is on the European exchange option.
The price of the exchange option will be determined from the CHO formula as the discounted expectation of the payoff  while the hedging portfolio will be obtained from the integrant in the martingale representation theorem setup of the the payoff. This integrant involves the Malliavin derivative of the payoff and its market price of risk and in the case that the latter is time-dependent, it reduces to the discounted expectation of the Malliavin derivative of
while the hedging portfolio will be obtained from the integrant in the martingale representation theorem setup of the the payoff. This integrant involves the Malliavin derivative of the payoff and its market price of risk and in the case that the latter is time-dependent, it reduces to the discounted expectation of the Malliavin derivative of  conditioned with respect to the filtration.
conditioned with respect to the filtration.
Preliminaries
The following is a summary of important results from [6] and [7]. One of the weaknesses of the delta hedging approach is its failure to justify fully the delta  because
because  may not be differentiable. Here
may not be differentiable. Here  represents the number of units of stock to be held at any time
represents the number of units of stock to be held at any time .
.
In this setup, if for example  , then
, then  is not differentiable everywhere. As a result, white noise theory justifies differentiability of
is not differentiable everywhere. As a result, white noise theory justifies differentiability of  in distribution. The differential operator is the Malliavin derivative
in distribution. The differential operator is the Malliavin derivative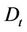 . This operator is defined in the space of distributions
. This operator is defined in the space of distributions 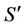 discussed fully in [6] and summarized below.
discussed fully in [6] and summarized below.
Let  be the Schwartz space of rapidly decreasing smooth functions and
be the Schwartz space of rapidly decreasing smooth functions and 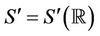 be its dual, which is the space of tempered distributions.Now, for
be its dual, which is the space of tempered distributions.Now, for  and
and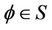 , let
, let  denote the action of
denote the action of  on
on , then by the Bochner-Minlows theorem, there exists a probability measure P on
, then by the Bochner-Minlows theorem, there exists a probability measure P on  such that
such that
 (1.1)
(1.1)
where . In this case P is called the white noise probability measure and
. In this case P is called the white noise probability measure and 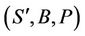 is the white noise probability space.
is the white noise probability space.
As a result, we shall be considering the space , as the sample space
, as the sample space , so that our asset prices will be defined on the probability space
, so that our asset prices will be defined on the probability space 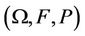 where
where 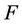 is the family of all Borel subsets of
is the family of all Borel subsets of . The construction of a version of the Brownian motion then is a direct consequence of the Bochner-Minlows theorem in that if
. The construction of a version of the Brownian motion then is a direct consequence of the Bochner-Minlows theorem in that if
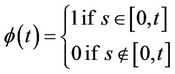 then clearly
then clearly  and thus
and thus
 so that immediately we conclude that
so that immediately we conclude that  where
where 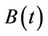 is normal with mean 0 and variance
is normal with mean 0 and variance . One can easily prove that
. One can easily prove that  is really a standard Brownian motion described in [7] as a continuous modification of the white noise process constructed above.
is really a standard Brownian motion described in [7] as a continuous modification of the white noise process constructed above.
The Brownian motion constructed this way is a distribution and thus special operations like the Malliavin derivative, defined below, are possible. Note that the Brownian motion is not differentiable in the classical sense but is differentiable in the Malliavin sense. The Malliavin derivative is a stochastic version of the directional derivative in classical calculus, with the direction carefully chosen. The following definition is from [7].
Definition 1.1 Assume that  has a directional derivative in all directions
has a directional derivative in all directions 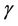 of the form
of the form  where
where  for fixed
for fixed , in the strong sense that
, in the strong sense that

exists in 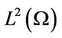 and assume further that there exists
and assume further that there exists 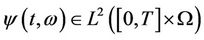 such that
such that
 , then we say that
, then we say that 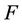 is differentiable and we call
is differentiable and we call
 the Malliavin derivative of
the Malliavin derivative of .
.
Just like any operation where using “first principles” is not usually easy operationally, one can use a series of characterizations to the above definition, which includes the chain rule, to compute the Malliavin derivative of any random variable which is differentiable. The set of all differentiable square integrable random variables was denoted by 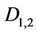 in [7]. As an illustration, we see that
in [7]. As an illustration, we see that  and the chain rule yield that,
and the chain rule yield that, . Here and elsewhere in this paper,
. Here and elsewhere in this paper, .
.
Therefore classically, one sees that the Malliavin derivative, in some sense, mimics differentiation in deterministic calculus. This is a big departure from Itô derivation which does not in any way make sense as a derivative in classical sense. Thus the space , the sample space, is rich enough to accommodate the concepts we require for our calculations.
, the sample space, is rich enough to accommodate the concepts we require for our calculations.
The paper is organized as follows: The next section gives the general pricing and hedging formulae for general contingent claims. The next section defines our market model and the final section gives our pricing and hedging results for the European exchange option.
2. General Pricing and Hedging Models in Complete Markets
We now consider the asset prices defined on the filtered probability space 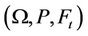 where
where  is the standard filtration generated by the Brownian motions, and which is rich enough to represent the information available to traders about all assets on the market at any time
is the standard filtration generated by the Brownian motions, and which is rich enough to represent the information available to traders about all assets on the market at any time .
.
The first security is a risk-free asset, e.g. bank account where the balance in the bank is  and is a solution of the deterministic differential equation
and is a solution of the deterministic differential equation
 (2.1)
(2.1)
under the assumption of existence of a unique solution . In this case
. In this case  is the interest rate which we shall later assume is constant for computational advantages.
is the interest rate which we shall later assume is constant for computational advantages.
The other securities are risky securities, e.g. stocks where for each , the price
, the price  of stock number
of stock number  is given by the Ito diffusion
is given by the Ito diffusion
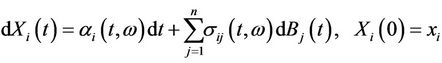 (2.2)
(2.2)
where 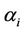 is the appreciation rate of security number
is the appreciation rate of security number 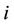 and
and  is the volatility coefficient of the Brownian motion
is the volatility coefficient of the Brownian motion  in security
in security .
.
Let 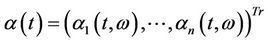 be the vector of appreciation rates for the stocks and the matrix
be the vector of appreciation rates for the stocks and the matrix

be the matrix of coefficients of volatility where for easy writing we suppressed dependence on time and noise and the risk factors are modeled by the  dimensional Brownian motion
dimensional Brownian motion
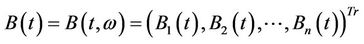 .
.
Then if , we have
, we have
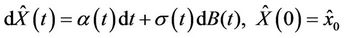 (2.3)
(2.3)
In all these cases we consider  for some finite time horizon T and throughout this paper, we are taking
for some finite time horizon T and throughout this paper, we are taking 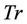 to mean transposition.
to mean transposition.
An investor who selects a portfolio consisting of the 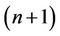 assets will have to work out the proportions of his wealth that he has to invest in each of the
assets will have to work out the proportions of his wealth that he has to invest in each of the 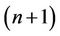 securities. The vector
securities. The vector 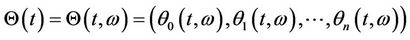 represents the investor’s holdings at any time
represents the investor’s holdings at any time , where for each
, where for each![]() ,
, ![]() is the number of units of security number
is the number of units of security number 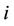 that the investor will hold.
that the investor will hold.
In future we shall refer to the vector of prices  as the market and the vector
as the market and the vector 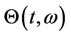 as the portfolio. The holder of a portfolio
as the portfolio. The holder of a portfolio  may decide to liquidate his position at any time
may decide to liquidate his position at any time , and his wealth is the cumulative savings in the bank account plus the trading gains up to and including the date of liquidation. We assume that the portfolio is self financing, so that, the value of this portfolio at time
, and his wealth is the cumulative savings in the bank account plus the trading gains up to and including the date of liquidation. We assume that the portfolio is self financing, so that, the value of this portfolio at time  is given by
is given by

The portfolio  is called admissible if it is self financing and the value process
is called admissible if it is self financing and the value process 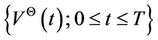 is bounded below.
is bounded below.
We note that by writing the value of the portfolio  as
as  and assuming that the portfolio is self financing and admissible, then, if
and assuming that the portfolio is self financing and admissible, then, if  is invertible, we have
is invertible, we have

where . If we let
. If we let
 , where
, where  is the vector of stock prices and if we further assume that
is the vector of stock prices and if we further assume that  satisfies the Novikov conditions, then, by the Girsanov theorem,
satisfies the Novikov conditions, then, by the Girsanov theorem,  given by
given by 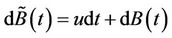 is a Brownian vector with respect to the probability measure
is a Brownian vector with respect to the probability measure 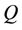 given by
given by
 .
.
In this case we are considering 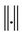 as the usual norm in
as the usual norm in .
.
Therefore
 (2.4)
(2.4)
Solving for  we get
we get
 (2.5)
(2.5)
From now on, without loss of generality, we assume constant coefficients. Then equation (2.5) becomes
 (2.6)
(2.6)
This is a particular version of the Martingale Representation Theorem which can be found for example, in [9] applied to a particular square integrable martingale  . It is this Martingale Representation theorem which the CHO formula relies on. We state here the theorem without proof and refer the reader to [6] for more details.
. It is this Martingale Representation theorem which the CHO formula relies on. We state here the theorem without proof and refer the reader to [6] for more details.
Theorem 2.1 (The generalized Clark-Ocone-Haussmann formula)
Suppose that  and assume that the following conditions hold:
and assume that the following conditions hold:
1) 
2) 
3) 
then

where 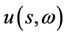 is the Girsanov kernel,
is the Girsanov kernel,  is the equivalent martingale measure and
is the equivalent martingale measure and  is a Brownian motion with respect to
is a Brownian motion with respect to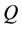 .
.
By letting 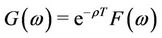 and applying the generalized CHO formula to
and applying the generalized CHO formula to , we have
, we have
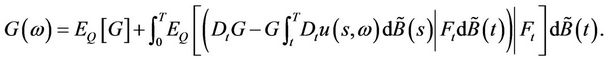 (2.7)
(2.7)
where  denotes the Malliavin derivative.
denotes the Malliavin derivative.
By uniqueness due to the Martingale Representation Theorem, we get
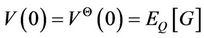 (2.8)
(2.8)
and
 (2.9)
(2.9)
where as before  and
and  means transpose.
means transpose.
Therefore
 (2.10)
(2.10)
This gives the explicit number of units of stocks. The holding  in the bank account can be found from the self financing condition.
in the bank account can be found from the self financing condition.
The importance of these results is that in a complete market, every contingent claim with payoff  is attainable by a portfolio of stocks and bonds. Therefore
is attainable by a portfolio of stocks and bonds. Therefore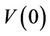 , the initial value of a self financing portfolio, equals the price of such a derivative, since
, the initial value of a self financing portfolio, equals the price of such a derivative, since  . It then shows that the time zero price of such a contingent claim is the discounted expectation of the payoff. Simplifying (2.8) depends on the nature of the payoff. One may directly compute the expectation on condition that the distribution of
. It then shows that the time zero price of such a contingent claim is the discounted expectation of the payoff. Simplifying (2.8) depends on the nature of the payoff. One may directly compute the expectation on condition that the distribution of  is known. Sometimes it may be easier to determine the BlackScholes partial differential equation satisfied by the value function with corresponding boundary conditions. If such a boundary value problem can be simplified explicitly, or through numerical techniques, then the price can be determined either explicitly or as a good approximation respectively. Other direct numerical methods of solution like the Monte Carlo simulations involve simulations of the underlying security itself and approximations of the expected values give estimate of (2.8). In this paper, we will find explicit results using some important change of measure transformations which we prove first.
is known. Sometimes it may be easier to determine the BlackScholes partial differential equation satisfied by the value function with corresponding boundary conditions. If such a boundary value problem can be simplified explicitly, or through numerical techniques, then the price can be determined either explicitly or as a good approximation respectively. Other direct numerical methods of solution like the Monte Carlo simulations involve simulations of the underlying security itself and approximations of the expected values give estimate of (2.8). In this paper, we will find explicit results using some important change of measure transformations which we prove first.
3. The Two Dimensional Market Model and Transformation Theorems
Suppose that traders will agree to trade an option which gives the holder the right, but not obligation to exchange a predetermined risky security with another predetermined risky security, then we call such an option an exchange option. We shall consider the case of a European exchange option. Suppose that the underlying securities in question have time  prices
prices  and
and  and to simplify our computations, we assume that the market consists of a bank account and these two stocks. The price of the bond is given by (2.1) albeit with constant force of interest
and to simplify our computations, we assume that the market consists of a bank account and these two stocks. The price of the bond is given by (2.1) albeit with constant force of interest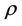 . The risky securities are given by
. The risky securities are given by
 (3.1)
(3.1)
where as before  is a standard Brownian motion.
is a standard Brownian motion.
Assume that these stochastic processes are defined on a filtered probability space  where
where  is a filtration for the assets such that the stochastic processes
is a filtration for the assets such that the stochastic processes ![]() are adapted. Suppose that at terminal time
are adapted. Suppose that at terminal time , then
, then  . Then the payoff of the exchange option will be
. Then the payoff of the exchange option will be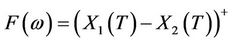 .
.
We want to determine the price and the hedging portfolio of this option by using the generalized CHO formula. We assume in our case that the coefficients are constant.
The Girsanov change of measure for this setup can be easily done by letting  where
where ;
;
 ;
;  and
and .
.
Then with constant coefficients, we can easily justify that  satisfies the Novikov conditions, so that the probability measure
satisfies the Novikov conditions, so that the probability measure  defined by
defined by
 (3.2)
(3.2)
is equivalent to  and
and 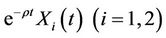 is a martingale with respect to
is a martingale with respect to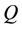 . In this case
. In this case
 is a
is a 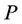 martingale.
martingale.
Moreover 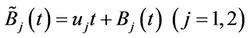 is a Brownian motion with respect to
is a Brownian motion with respect to . Let
. Let
 .
.
With respect to  price
price  is
is

so that

is a Q-martingale.
In order to exploit the results from the previous discussions, we note here that the market  is a special case of the
is a special case of the  -dimensional market considered in the previous section with n = 2 in this case. We assume that
-dimensional market considered in the previous section with n = 2 in this case. We assume that  is invertible so that the market is complete. Therefore if we choose a self financing portfolio
is invertible so that the market is complete. Therefore if we choose a self financing portfolio  which is also admissible, then the discounted value of the portfolio at any time
which is also admissible, then the discounted value of the portfolio at any time  is given by
is given by

where .
.
In this case we note that from the CHO formula , for any contingent claim , we get
, we get
 (3.3)
(3.3)
and
 (3.4)
(3.4)
where 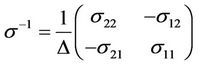 and
and
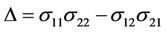 .
.
Note that since we have assumed that the market is complete, then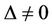 .
.
Transformation Theorems
In order to facilitate our computation and taking advantage of the distribution of the terminal values of the underlying securities  and
and , we provide some important transformation results. Their usefulness will be evident in simplifying both (3.3) and (3.4).
, we provide some important transformation results. Their usefulness will be evident in simplifying both (3.3) and (3.4).
Proposition 3.1 Let  and
and  be two independent standard normal random variables and let
be two independent standard normal random variables and let . Define a probability measure
. Define a probability measure  equivalent to
equivalent to  with density
with density
 .
.
Then the random Gaussian variable 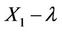 and
and  are independent standard normal variables with respect to
are independent standard normal variables with respect to .
.
Proof.
We have to prove first that  and
and  are independent normally distributed random variables with respect to the probability measure
are independent normally distributed random variables with respect to the probability measure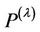 .
.
Recall that a random variable 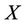 with mean
with mean
 and variance
and variance  is normally distributed if its characteristic function is
is normally distributed if its characteristic function is
 In our case we have
In our case we have

Therefore  is normal with mean
is normal with mean  and variance 1, with respect to
and variance 1, with respect to . Therefore
. Therefore  is normal with mean zero and variance 1 with respect to
is normal with mean zero and variance 1 with respect to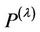 .
.
In the same way we can show that 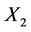 is normal with mean
is normal with mean

and variance 1 since
 .
.
To prove that  and
and  are independent with respect to
are independent with respect to  it suffices to prove that
it suffices to prove that  and
and  are uncorrelated , that is,
are uncorrelated , that is, .
.
Now

Corollary 3.1
Let  and
and  be as given in Proposition 3.1 and let
be as given in Proposition 3.1 and let  and
and  be real numbers. Then
be real numbers. Then

where  and
and 
Proof.
We have

By using the notation in Proposition 3.1, then the previous expression can be re-written
 (6)
(6)
We have shown in Proposition 3.1 that the random variables 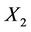 and
and  are standard normal distritions with respect to
are standard normal distritions with respect to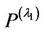 , so that with respect to the same probability measure, the random variable
, so that with respect to the same probability measure, the random variable  has a normal distribution with mean zero and variance
has a normal distribution with mean zero and variance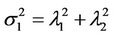 . In the same way, with respect to
. In the same way, with respect to , the random variables
, the random variables 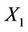 and
and  are standard normal distributions so that
are standard normal distributions so that  is a normal distribution with mean zero and variance
is a normal distribution with mean zero and variance .
.
Therefore (6) becomes
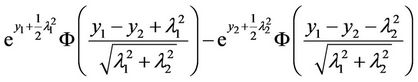 □
□
Remark 3.1
Proposition 3.1 still holds in an m-dimensional case where both  and
and  are independent multivariate standard normal random vectors. In that case, the following results will be extensions of the preceding proposition and corollary respectively.
are independent multivariate standard normal random vectors. In that case, the following results will be extensions of the preceding proposition and corollary respectively.
Proposition 3.2
Let  and
and 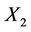 be two independent m-dimensional normal random vectors each with mean equal to the zero vector and covariance matrix equal to the identity matrix and let
be two independent m-dimensional normal random vectors each with mean equal to the zero vector and covariance matrix equal to the identity matrix and let  be any non-zero vector. Define a probability measure
be any non-zero vector. Define a probability measure , equivalent to
, equivalent to  with density
with density , where
, where  is the usual norm in
is the usual norm in .
.
Then 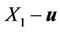 and
and  are independent Gaussian vectors with zero mean (vector) and covariance matrix equal to the identity.
are independent Gaussian vectors with zero mean (vector) and covariance matrix equal to the identity.
Consequently Corollary 3.1 can be extended as follows:
Corollary 3.2 Let  and
and  be as in Proposition 3.2 and let
be as in Proposition 3.2 and let  and
and  be real numbers. If
be real numbers. If  and
and  are m-dimensional vectors, then
are m-dimensional vectors, then

where 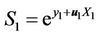 and
and  and
and  denotes the usual norm in
denotes the usual norm in .
.
4. Price and Hedging Portfolio of an Exchange Option
Note that if, for a fixed time horizon , the random variables
, the random variables  and
and 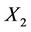 in the previous proposition are Brownian vectors
in the previous proposition are Brownian vectors  and
and  respectively, then the equivalent probability measure
respectively, then the equivalent probability measure  will be given by the density
will be given by the density 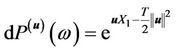 and we would also insist that the vector
and we would also insist that the vector  satisfy the Novikov conditions.
satisfy the Novikov conditions.
We are now ready give the price and hedging portfolio of the European exchange option.
4.1. Price of a European Exchange Option
Proposition 4.1 The price of the European exchange option is given by

where  is the cumulative distribution function of the standard normal distribution.
is the cumulative distribution function of the standard normal distribution.
Proof.
We had noted that with respect to the equivalent martingale measure  which we defined, the prices of the two underlying assets
which we defined, the prices of the two underlying assets  and
and  are given by
are given by

where  and
and
 .
.
Therefore the time zero price of the European exchange option is

If we define the probability measure  equivalent to
equivalent to 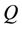 by
by , then
, then

By using the results of the previous proposition, we then conclude that the time zero price of the European exchange option is given by  where
where

and

Note that .
.
Moreover, since  and
and
 , then
, then  and ss
and ss
 so that the time zero price of the European exchange option becomes
so that the time zero price of the European exchange option becomes

Note that this price does not depend on the appreciation rates of the stocks nor on the market interest rate , but just on the market volatilities. This result is also similar to the one obtained in [1] but in that paper the author considers the case when the Brownian motions are correlated and also with a special assumption that the noise terms for each stock are different. We have allowed that stock prices to depend on the two Brownian motions.
, but just on the market volatilities. This result is also similar to the one obtained in [1] but in that paper the author considers the case when the Brownian motions are correlated and also with a special assumption that the noise terms for each stock are different. We have allowed that stock prices to depend on the two Brownian motions.
4.2. Hedging an Exchange Option
We now calculate the hedging portfolio 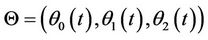 . For this two dimensional case, thanks to the CHO formula, we get, from (2.9), that
. For this two dimensional case, thanks to the CHO formula, we get, from (2.9), that
 , where, as before
, where, as before
 , with
, with  and
and
 .
.
Now

where
 . Therefore
. Therefore

We thus have the following result Proposition 4.2 The perfect hedge  is given by
is given by

and

where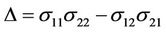 ,
,

and

Proof.
In order to calculate , we need to use the Markov property . We first calculate
, we need to use the Markov property . We first calculate  as follows:
as follows:

where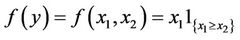 .
.
Therefore the previous expression becomes
 .
.
Note that, with respect to , we have
, we have
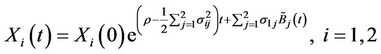 .
.
Therefore since  is independent of
is independent of 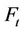 then
then

where

Using the previous notations of  and
and , then the previous expression reduces to
, then the previous expression reduces to

where .
.
Now, with respect to 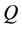 and for each j = 1, 2 we have
and for each j = 1, 2 we have  is a normal distribution with zero mean and variance
is a normal distribution with zero mean and variance 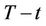 then
then  is a normally distributed random vector with mean zero (vector) and covariance matrix equal to the identity matrix. Moreover the previous expression becomes
is a normally distributed random vector with mean zero (vector) and covariance matrix equal to the identity matrix. Moreover the previous expression becomes

where

Therefore

with

where
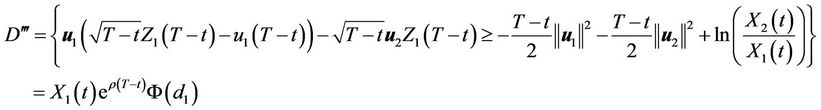
where

In the same way we can also calculate  to get the result as
to get the result as  where
where

In summary we have
 .
.
Therefore the equation  gives
gives
 .
.
Solving for  and
and  we get:
we get:

and

where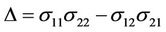 .
.
The number of units in the bond, at any time  will be computed from the expression
will be computed from the expression
 □
□
To the best of our knowledge, this result has not been obtained before in its explicit form. However, since the market is Markovian, we could still check this result of the hedging portfolio by differentiating the value function with respect to the stock prices 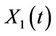 and
and .
.
5. Conclusion
We have shown that white noise analysis is of vital importance to Finance in that the generalized CHO formula becomes important in finding explicit expressions for the price and hedging portfolio of European contingent claims. Extensions of these results would be to get similar explicit results when modelling stock prices with general Itô-Lévy processes, though one has to carefully consider the models of prices to avoid incompleteness. Hedging an option is important in that the seller would know how much of each security to hold in order to hedge his liability. In complete markets, this should always be possible and thus the results in this paper can be applied to any European contingent claim. The [1] opened the door for pricing the exchange options though in that paper, the stock prices were influenced each by one Brownian motion and the two were given as correlated. In our case, we allowed the stock prices to each depend on the two noise terms which are independent. Also in our paper, we have computed explicitly, the hedging portfolio, something which was not done in [1]. As a result, our results are extensions of that paper with the strength of using white noise analysis.
6. Acknowledgements
This work was supported by the University of Cape Town Research Grant 461091 .
REFERENCES
- W. Margrabe, “The Value of an Option to Exchange One Asset for Another,” Journal of Finance, Vol. 33, No. 1, 1978, pp. 177-186. doi:10.1111/j.1540-6261.1978.tb03397.x
- T. Hida, H.-H. Kuo, J. Potthoff and L. Streit, “White Noise,” Kluwer, Dordrecht, 1993.
- T. Hida and J. Potthof, “White Noise Analysis—An Overview, White Noise Analysis: Mathematics and Applications,” World Scientific, Singapore, 1989.
- H. H. Kuo, “White Noise Distribution Theory,” CRC Press, Boca Raton, 1996.
- N. Obata, “White Noise Calculus and Fock Space,” Springer-Verlag, Berlin, 1994.
- K. Aase, B. Oksendal, N. Privault and J. Uboe, “White Noise Generalizations of the Clark-Haussmann-Ocone Theorem, With Application to Mathematical Finance,” Finance and Stochastics, Vol. 4, No. 4, 2000, pp. 465- 496. doi:10.1007/PL00013528
- B. Øksendal, “An introduction to Malliavin Calculus with Applications to Economics,” Working Paper 3/96, Institute of Finance and Management Science, Norwegian School of Economics and Business Administration, Bergen, 1996.
- I. Karatzas and D. Ocone, “A Generalized Clark Representation Formula, with Application to Optimal Portfolios,” Stochastics and Stochastic Reports, Vol. 34, 1991, pp. 187-220.
- B. Øksendal, “Stochastic Differential Equations,” 5th Edition, Springer-Verlag, Berlin, 2000.

