Received 30 December 2015; accepted 23 February 2016; published 26 February 2016

ABSTRACT

In financial field, outliers represent volatility of stock market, which plays an important role in management, portfolio selection and derivative pricing. Therefore, forecasting outliers of stock market is of the great importance in theory and application. In this paper, the problem of predicting outliers based on adaptive ensemble models of Extreme Learning Machines (ELMs) is considered. We found out that the proposed model is applicable for outlier forecasting and outperforms the methods based on autoregression (AR) and extreme learning machine (ELM) models.

Keywords:

Component, Extreme Learning Machine, Outliers Forecasting, Wavelet Transform

1. Introduction

Outliers can have deleterious effects on statistical analyses. They can result in parameter estimation biases, invalid inferences and weak volatility forecasts in financial data. As a result when modeling financial data, their detection and correction should be considered seriously. Time-series data are often messed up with outliers due to the influence of unusual and non-repetitive events. Forecast accuracy in such situations is decreased dramatically due to a carry-over effect of the outliers on the point forecast and a bias in the estimate of parameters. The effect of additive outliers on forecasts is studied by Ledolter [1] . It was shown that forecast intervals are quite sensitive to additive outliers, but that point forecasts are largely unaffected unless the outlier occurs near the forecast origin. In such a situation the carry-over effect of the outlier can be quite substantial.

Considerable research has been devoted to the subject of forecasting and various methods have been suggested which have been divided into two main groups: classical methods mainly exponential smoothing, regression, Box-Jenkins autoregressive integrated moving average (ARIMA), generalized autoregressive conditionally heteroskedastic (GARCH) methods, and modern methods applying artificial intelligence techniques including artificial neural networks (ANN) and evolutionary computation (for more discussed details see [2] -[4] ). Extreme learning machine (ELM) has been proposed as a class of learning algorithm for single hidden layer feedforward neural networks (SLFNs). In ELM algorithm, the connections between the input layer and the hidden neurons are randomly assigned and remain unchanged during the learning process. Thus by minimizing the cost function through a linear system the output connections are tuned. The computational burden of ELM has been significantly reduced as the only cost is solving a linear system. The low computational complexity attracted a great deal of attention from the research community, especially for high dimensional and large data applications. While considerable research has been devoted to detecting and removing outliers, few focused on forecasting them.

Outliers forecasting model has been discussed in [5] for the two market indexes and six individual stocks based on multi-feature extreme learning machine (ELM) algorithm. The purpose of this paper is to present adaptive ensemble model of Extreme Learning Machines (ELMs) for prediction which can lead to smaller predicting errors and more accuracy than some other forecasting methods. This paper is structured as follows: In Section 2, the theories of wavelet transform and ELM are presented, as well as how we combine both of them in the adaptive ensemble method. Section 3 describes the numerical studies, while Section 4 discusses the results.

2. Methodology

In this section, we present the methodology employed for forecasting outliers applying a wavelet decomposition technique and ELM algorithm.

2.1. Wavelet Transforms

This section contains some facts about wavelets, used throughout this paper. A thorough review of the wavelet transform is discussed in Mallat [6] -[8] . The wavelet analysis is a mathematical tool that offers decomposition of signal s(t) into many frequency bands at many scales. In particular, the signal s(t) is decomposed into smooth coefficients α and detail coefficients d, which are given by

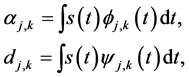
where Φ is the father and Ψ is the mother wavelets, and j and k are, respectively, the scaling and translation parameters. The father wavelet (function) keeps the frequency domain properties (low-frequency) of the signal, while the mother wavelet keeps the time domain properties (high-frequency). The father wavelet Φ and the mother wavelet Ψ are defined as follows:

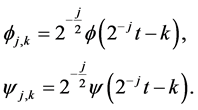
The two wavelets Φ and Ψ satisfy the condition 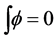and. Consequently, the orthogonal wavelet

representation of the signal s(t) is given by

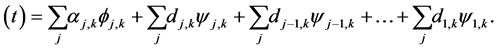
Using the above decomposition, the original signal s(t) is represented with approximation coefficients α(t) and detail coefficients d(t), by convolving the signal s(t) with a low-pass filter (LP) and a high-pass filter (HP), respectively. The low-pass filtered signal is the input for the next iteration step and so on. The approximation coefficients α(t) contain the general trend (the low-frequency components) of the signal s(t), and the detail coefficients d(t) contain its local variations (the high-frequency components).

2.2. Extreme Learning Machine (ELM) Algorithm

The purpose of this paper is to discuss the mythology behind the Extreme learning machine (ELM). ELM is an improved learning algorithm for the single feed-forward neural network structure. It notably differs from the traditional neural network methodology, since it is not essential to tune all the parameters of the feed-forward networks (input weights and hidden layer biases). For more information on efficiency of SLFNs with randomly chosen input weights, hidden layer biases and a nonzero activation function to approximate any continuous functions on any input set, one can refer to [9] and [10] .

The proposed extreme learning machine (ELM) has shown its efficiency in training feedforward neural networks and overcoming the limitations faced by other conventional algorithms [11] [12] . The essences of ELM lie in two aspects, that is, random neurons and the tuning-free strategy. The learning phase of ELM generally includes two steps, namely, constructing the hidden layer output matrix with random hidden neurons and finding the output connections. Thanks to using random hidden neuron parameters which remain unchanged during the learning phase, ELM enjoys a very low computational complexity. The computational burden has been greatly reduced as the only cost is solving a linear system. At the same time, numerous applications have shown that ELM can provide a comparable or better generalization performance than the popular support vector machine (SVM) [13] [14] and the BP method in most cases [15] -[17] .

ELM is a single-hidden layer feedforward network (SLFN) with a special learning mechanism which is consists of three layers: input layer, hidden layer and output layer. Suppose the SLFN has n hidden nodes and nonlinear activation function g(x). For N training samples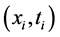, where 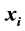is the ith input vector and t_i is the ith desired output, the SLFN can be modeled by

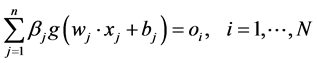
where 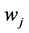is the input weight vector linking the jth hidden node and the input nodes, is the bias of the jth hidden node, 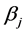is the output weight vector linking the jth hidden node and the output nodes, 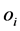is the actual network output. If ELM can approximate all the training samples with zero error, then we claim that there exist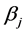, and such that

The above matrix can be expressed as Hβ = T, where H is called the hidden layer output matrix. As mentioned earlier, the input weights and hidden biases are randomly constructed and do not need tuning as in the case of traditional SLFN methodology. The evaluation of the output weights linking the hidden layer to the output layer is equivalent to determining the least-square solution to the given linear system. The minimum norm least-square (LS) solution to the linear system is

The H in the above equation is the Moore-Penrose (MP) generalized inverse of matrix H, see [18] for more discussion. The minimum norm LS solution is unique and leads to smallest norm along all the LS solutions. The MP inverse method based on ELM algorithm is found to obtain a good generalization performance with a radically increased learning speed. One can present a general Algorithm for ELM as follows. For a given training set, activation function g(x) and hidden neuron number L:

Step 1: Assign random input weight and bias,.

Step 2: Calculate the hidden layer output matrix H.

Step 3: Calculate the output weight.

Theoretical discussions and a more thorough presentation of the ELM algorithm are detailed in the original papers [19] [20] .

2.3. Adaptive ELM

Comparable to other flexible nonlinear estimation methods, the ELM may suffer either under-fitting or over-fit- ting [19] . Over-fitting is particularly inaccurate since it can cause wild prediction far beyond the range of the training data even with the noise-free data. It may lead to poor predictive performance, as it may cause minor fluctuations in the data. In this work, the output of the network is only one value that is the predicted outliers.

The ensemble model is made up of a number of randomly initialized ELMs, which each have their own parameters. The model has an associated weight which determines its contribution to the prediction of the ensemble. Hence, we present our model only for one output. Let us define the input data as

Comparing to the learned input patterns which is presented as

The determination of the closeness measure is the major factor in prediction accuracy, for which adaptive metrics are introduced to solve this problem and the arithmetic is defined by:

Studying time-series forecasting, the information on trends and amplitudes plays an effective role. Adaptive metrics are introduced to solve this problem, while the arithmetic is presented as:

(1)

where the parameter of minimization, equilibrates the amplitude difference between and and

,

where and are the largest and smallest elements of vector correspondingly,

. The optimization problem (1) can be solved using the algorithm of Levenberg-

Marquardt optimization or other gradient methods for . For, two equations may presented as blow:

Then the solution of the minimization problem can be obtained analytically:

where, j = 1,2,. The adaptive k-nearest neighbors are chosen and the

input vector of the first network can be defined as:

.

The forecasting error increases considerably because of the big difference between training data and input data. In order to get more accurate results for time series, k sets of inputs are used and the output vector are. The mechanism for admixture of outputs is presented as follows:

where is the distance between Q_i’s vth nearest pattern and Q_i. The model has been tested on both stationary and nonstationary time series, and the experiments show that in both cases the adaptive ensemble method leads to a prediction accuracy comparable to the best methods. For more detailed information see [16] [17] .

3. Numerical Studies

The data used in the paper is the daily value of Petroleum sector Index, obtained from the DataStream database services of Tehran Over-the-Counter Market (OTC)¹. Since 2009, Iran has been developing an over-the-counter market for bonds and equities. OTC provides a complete available achieve of data, based on different sectors and dates. Our sample ranges from 28 Sep 2009 to 27 Dec 2015, with 1510 observations. Petroleum, the prime reason for the economic growth of the country, has been the primary industry in Iran since the 1920s. In 2012, Iran was the second-largest exporter among the Organization of Petroleum Exporting Countries², which exports around 1.5 million barrels of crude oil a day. Through primary wavelet decomposition, sequence V’s low frequency and high frequency are computed. In order to eliminate stochastic diffusion we set high frequency equal zero. To get the main trend, inverse wavelet transform is used for low frequency Then we compute the absolute residual of V as sequence

Based on sequences obtained from Matlab, we then construct an AD-ELM abnormal predicting model which can predict whether abnormal fluctuation will appear today or not. Since an ELM is essentially a linear model of the responses of the hidden layer, we apply PRESS statistics in R to retrain the ELM in an incremental way. The number of input nodes for ELM, and AD-ELM are set as 10, and the number of hidden is set to be 5. A detailed discussion of inputs and hidden nodes of ELMs with PRESS can be found in [21] . Figure 1 shows the outliers in green color, while the red plus signs (115 points) represent abnormal points.

In order to analyze outlier detection accuracy of AD-ELM method with other methods, an adequate error measure method must be selected. In this paper we apply mean squared error (NMSE) and Mean Absolute Percentage Error (MAPE). The first is used as the error criterion, which is the ratio of the mean squared error to the variance of the time series, while the second on is regarded as one of the standard statistical performance measures. For a time series we have

where is the predicted point and N is the number of predicted points.Different prediction models on the data is summarized in Table 1. In our work, the AR method using AR(m)

where m is the number of input nodes of AD-ELM. In the simulation, the NMSE are 1.5678, 0.6345, and 0.08436 for AR, ELM, AD-ELM respectively, and the MAPE are 42.65%, 12.54%, 9.54% for AR, ELM, AD-ELM respectively. It is undeniable that the AD-ELM method improves upon the two other models.

4. Results and Conclusion

In this paper, forecasting models mostly have been used to forecast the stock market index value outliers. The proposed AD-ELM method is successfully used for market indexes of Tehran Over-the-Counter Market (OTC) for Petroleum sector for 1510 observations. Outliers of time series are firstly calculated through wavelet decomposition and then prediction is constructed using AD-ELM method. We plot outlier detection and evaluate forecast accuracy by mean squared error and Mean Absolute percentage error. The results reveal successfully that the accuracy of the proposed method can lead to smaller NMSE (0.08436) and MAPE (9.45%); comparing to autoregression (AR) and extreme learning machine (ELM) models, thus the AD-ELM method is a superior method for the practical forecasting of time series.

Acknowledgements

This research is supported by ‎Payame Noor University‎, ‎19395-4697‎, ‎Tehran‎, Iran. The author gratefully acknowledges the constructive comments, offered by anonymous referee which help to improve the quality of the paper significantly.

Cite this paper

NargessHosseinioun, (2016) Forecasting Outlier Occurrence in Stock Market Time Series Based on Wavelet Transform and Adaptive ELM Algorithm. Journal of Mathematical Finance,06,127-133. doi: 10.4236/jmf.2016.61013

References

NOTES

¹http://www.ifb.ir.

²Energy and the Iranian economy. United States Congress. July 25, 2006. Retrieved June 11, 2014.