Wireless Engineering and Technology
Vol.4 No.2(2013), Article ID:29793,6 pages DOI:10.4236/wet.2013.42010
A New Improved Symbol Mapper/8-Ary Constellation for BICM-ID
![]()
1Telecommunications and Digital Signal Processing Laboratory, Djillali Liabes University, Sidi Bel-Abbes, Algeria; 2Department of Electronics Engineering, M’sila University, M’sila, Algeria.
Email: slimane34a@yahoo.fr, adjebari2002@yahoo.fr
Copyright © 2013 Slimane Benmahmoud, Ali Djebbari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 23rd, 2012; revised February 2nd, 2013; accepted February 16th, 2013
Keywords: Bit Interleaved Coded Modulation; BICM; Iterative Decoding/Processing; Log-Likelihood Ratios (LLRs); 8PSK Constellation; Signal Mappings; Constellation Labeling Maps; Extrinsic Information; BCJR Algorithm
ABSTRACT
This contribution proposes a new combination symbol mapper/8-ary constellation, which is a joint optimization of an 8-ary signal constellation and its symbol mapping operation, to improve the performance of Bit Interleaved Coded Modulation with Iterative Decoding (BICM-ID). The basic idea was to use the so called (1,7) constellation (which is a capacitive efficient constellation) instead of the conventional 8-PSK constellation and to choose the most suitable mapping for it. A comparative study between the combinations most suitable mapping/(1,7) constellation and SSP mapping/conventional 8-PSK constellation has been carried out. Simulation results showed that the 1st combination significantly outperforms the 2nd combination and with only 4 iterations, it gives better performance than the 2nd combination with 8 iterations. A gain of 4 dB is given by iteration 4 of the 1st combination compared to iteration 8 of the 2nd combination at a BER level equal to 10−5, and it (iteration 4 of the 1st combination) can attain a BER equal to 10−7 for, only, a SNR = 5.6 dB.
1. Introduction
A straightforward concatenation of a convolutional encoder and an M-ary modulator doesn’t provide the best performance. A joint design of a convolutional encoder and a multi-level/phase modulator, called Trellis Coded Modulation (TCM) [1], maximizes the minimum squared Euclidian distance to provide a significant improvement over AWGN channels but it doesn’t provide the same improvement over Rayleigh fading channels.
Symbol interleaving is used to make TCM system memoryless and its diversity order is then defined as the minimum number of distinct symbols between two codewords [2].
By replacing symbol interleaving by bit-level interleaving in TCM, Zehavi in [2], succeeded to increase the diversity order to the binary Hamming distance of the coded system.
The scheme proposed by Zehavi, called later in [3] Bit Interleaved Coded Modulation (BICM), achieves better performance than Ungerboeck’s TCM over Rayleigh fading channels.
Bit interleaving in BICM causes random modulation which reduces the free Euclidian distance that makes BICM significantly worse than Ungerboeck’s TCM over AWGN channels [2-4].
Turbo codes were introduced in 1993 by Berrou et al. [5]. The results of iterative decoding, applied for turbo codes, motivated authors of [6] to apply it (iterative decoding) for BICM which led to BICM with Iterative Decoding (BICM-ID). ID greatly improves the BICM’s performance over both AWGN and Rayleigh fading channels.
With a suitable design of the mapping function for a given constellation, BICM-ID can attain an excellent performance [7]. In this later reference, Gray, SP and SSP mappings were considered and a comparison of these labeling schemes for 8PSK constellation has been done. It has been found that SSP mapping offers the best performance.
Authors of [8] presented various optimal non-orthogonal 16-QAM mappings and an improvement of 0.2 dB has been shown compared to the state of the art orthogonal QAM constellation with approx. the same error floor.
A new mapping scheme, called the Maximum Squared Euclidian Weight (MSEW), has been introduced in [9].
The objective of this paper was to jointly optimize an 8-ary constellation and its symbol mapping operation to improve the performance of BICM-ID. To do so, the BER performances of the seven proposed mappings for (1,7) constellation were examined by simulation in order to choose the most suitable mapping for this constellation.
In [10] we found that SSP is the suitable mapping for conventional 8-PSK constellation and for rectangular 8-QAM constellation also [11,12].
Based on these results, a comparative study between the combinations most suitable mapping/(1,7) constellation and Semi-Set Partitioning (SSP)/conventional 8-PSK constellation has been carried out .
In this paper we show that BICM-ID, using a new proposed symbol mapper/8-ary constellation’s combination, can provide excellent performance compared to it using the well-known SSP mapping/conventional 8-PSK constellation’s combination.
The rest of the paper is organized as follows. In Section 2, we present the BICM-ID system’s model and its iterative processing process. Then in Section 3, we talk about (1,7) constellation and different mappings used in this study. We talk also about conventional 8-PSK constellation and SSP mapping. We present and discuss simulation results in Section 4. Section 5 concludes this paper. Finally, Appendix gives further simulation results on the performance of (1,7) constellation and its mappings.
2. BICM-ID System’s Model
2.1. BICM-ID System’s Overview
Figure 1 illustrates the bloc diagram of a BICM-ID’s transceiver. Its transmitter (Figure 1(a)) consists of a serial concatenation of a conventional encoder, a bitinterleaver and an M-ary (8-ary in our case) constellation mapper.
Data bits u are first encoded by the convolutional encoder. Then, the bit-interleaver permutes the encoded bits c to form a sequence of interleaved bits v. Each m = log2M (m = 3 in our case) successive interleaved bits will be grouped in one symbol . The resulting m-bits symbols are then mapped into complex symbols si in the constellation set Ψ (with M = 2m symbols) according to the following rule
. The resulting m-bits symbols are then mapped into complex symbols si in the constellation set Ψ (with M = 2m symbols) according to the following rule
 (1)
(1)
For conventional 8-PSK constellation: M = 8 symbols,
 (a)
(a) (b)
(b)
Figure 1. BICM-ID’s, based 8-ary constellation, transceiver. (a) Transmitter; (b) Receiver.
m = log2M = 3 bits, v = (v1, v2, v3),  , and
, and
 (2)
(2)
The resulting complex symbols are then passed through a discrete-time channel (for a base band model). The received discrete-time signal, for a Rayleigh fading channel is given by
 (3)
(3)
where ai is the fading coefficient, which can be represented by a Rayleigh random variable, and ni is a sample of an AWGN with a zero mean and a variance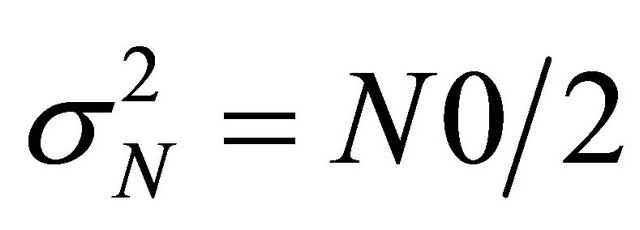 , where N0 is the unilateral power spectral density of a white Gaussian noise. For AWGN channel, we take ai = 1.
, where N0 is the unilateral power spectral density of a white Gaussian noise. For AWGN channel, we take ai = 1.
2.2. Iterative Decoding with Soft Decision Feedback for BICM
Contrary to decoding algorithms that uses hard decision, like the Viterbi algorithm used for convolutional codes, a Soft-Input Soft-Output (SISO) module is used for BICMID. This SISO decoder uses a Maximum A Posteriori (MAP) algorithm to compute the Log-Likelihood Ratios (LLRs) of coded and data bits (Figure 1(b)). Practically, this MAP algorithm is implemented in the logarithmic domain to reduce numerical computations and complexity.
During the first iteration, the demapper is fed with the received signal ri. The second input  (the a priori information of the interleaved bits) is set to zero during the first iteration, since no prior information is available on the input bits v (the interleaved bits) of the constellation mapper. The demapper computes the a posteriori LLRs
(the a priori information of the interleaved bits) is set to zero during the first iteration, since no prior information is available on the input bits v (the interleaved bits) of the constellation mapper. The demapper computes the a posteriori LLRs  of the interleaved bits which will be used to calculate their extrinsic LLRs using the following equation
of the interleaved bits which will be used to calculate their extrinsic LLRs using the following equation
 (4)
(4)
This operation is shown by the lower subtraction path in Figure 1(b).
The extrinsic LLRs  are then passed through the de-interleaver to create the a priori LLRs
are then passed through the de-interleaver to create the a priori LLRs  of coded bits. The a priori LLRs
of coded bits. The a priori LLRs  of data bits is always set to zero, which implies equally likely transmitted source’s data bits. The a posteriori LLRs
of data bits is always set to zero, which implies equally likely transmitted source’s data bits. The a posteriori LLRs  of data bits will be used in final iteration to recover the data bits using hard decision according to the next rule
of data bits will be used in final iteration to recover the data bits using hard decision according to the next rule
 (5)
(5)
On the other hand, the a posteriori LLRs  of coded bits are used to calculate the extrinsic LLRs
of coded bits are used to calculate the extrinsic LLRs  of coded bits using the following equation
of coded bits using the following equation
 (6)
(6)
The later operation is shown by the upper subtraction path in Figure 1(b).
The extrinsic LLRs  are then fed back through the interleaver to create the a priori LLRs
are then fed back through the interleaver to create the a priori LLRs  of interleaved bits, which will be passed to the demapper to start a second iteration, and the cycle of iterations is repeated until a stopping condition.
of interleaved bits, which will be passed to the demapper to start a second iteration, and the cycle of iterations is repeated until a stopping condition.
Since the interleaver makes m bits in one symbol independent, the a priori information  of each transmitted signal
of each transmitted signal  is given as in [8] by
is given as in [8] by
 (7)
(7)
where,  is the value of the
is the value of the  bit in the label of
bit in the label of .
.
The demapper generates a posteriori LLRs  as follows
as follows
 (8)
(8)
By substituting Equation (8) in Equation (4), we find
 (9)
(9)
where, . The amplitude’s fading coefficient ai is assumed perfectly estimated.
. The amplitude’s fading coefficient ai is assumed perfectly estimated.
From (9), we can observe that  is computed from the a priori LLRs
is computed from the a priori LLRs  of other interleaved bits (j ≠ k) in the same symbol.
of other interleaved bits (j ≠ k) in the same symbol.
3. (1,7) Constellation and the Proposed Mappings
The bijection between the binary m-bits’ symbols and the complex symbols of the constellation set is called symbol mapping.
For a given number of bits (the value of m) that should be transmitted per symbol, the signal constellation and the mapping method must be specified.
The (1,7) constellation’s symbols set is given by
 (10)
(10)
These symbols are shown in Figure 2(a) accompanied with the symbols of conventional 8-PSK constellation in Figure 2(b).
In Table 1, we show the seven different mapping methods (called MAP1, MAP2,  , MAP7) for (1,7) constellation and the SSP mapping used for conventional 8-PSK constellation. SSP mapping is widely used in the literature because it maximizes diversity by assigning binary labels which differ at least in two bits to adjacent symbols in the constellation diagram. For example, in the conventional 8-PSK constellation, the two binary labels 100 and 001 are assigned to adjacent points.
, MAP7) for (1,7) constellation and the SSP mapping used for conventional 8-PSK constellation. SSP mapping is widely used in the literature because it maximizes diversity by assigning binary labels which differ at least in two bits to adjacent symbols in the constellation diagram. For example, in the conventional 8-PSK constellation, the two binary labels 100 and 001 are assigned to adjacent points.
In practice, to compute the a posteriori LLRs  of the interleaved bits (demapping operation), we need to divide the constellation set
of the interleaved bits (demapping operation), we need to divide the constellation set  into two subsets
into two subsets  for each position k where b = 0,1 (the bit’s binary value). For a MAP3 mapped (1,7) constellation (Figure 2(c)), we have the following constellation’s sub-sets
for each position k where b = 0,1 (the bit’s binary value). For a MAP3 mapped (1,7) constellation (Figure 2(c)), we have the following constellation’s sub-sets
 (a)
(a) (b)
(b)
Figure 2. The two used constellations: (a) and (b) their symbols’ positions; (c) Sub-sets partition for (1,7) constellation (MAP3 is considered).
Table 1. (1,7) constellation and the seven used mappings (MAP1, MAP2, ∙∙∙, MAP7).

 (11)
(11)
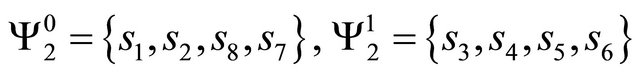 (12)
(12)
 (13)
(13)
In Figure 2(c), a filled (respectively an unfilled) circle represents a symbol for which the binary label has the value b = 1 (respectively b = 0) in the kth bit’s position.
4. Simulation Results
4.1. Simulation Parameters
In this contribution, we use a 4-states, rate 1/2 non-recursive and non-systematic (NSC) convolutional encoder with the generator polynomials . The random bit-interleaver is of length 6138 coded bits. For each BER point we simulate almost 10+8 data bits, and we count at least 100 erroneous bits. The Max-log-MAP version of the BCJR algorithm is used for the decoding of the NSC code. A Rayleigh fading channel model is considered.
. The random bit-interleaver is of length 6138 coded bits. For each BER point we simulate almost 10+8 data bits, and we count at least 100 erroneous bits. The Max-log-MAP version of the BCJR algorithm is used for the decoding of the NSC code. A Rayleigh fading channel model is considered.
4.2. The BER Performance of BICM-ID
Figure 3 explicitly compares the BER performances of these seven mappings after 8 iterations.
These results show that MAP3 is the most suitable (between all used mappings) mapping for (1,7) constellation. For example, with MAP3 we can achieve a BER equal to 5 × 10−8 for 6 dB (Figure 3).
From Figure 3, we can also remark that to achieve better performance we can use MAP4 for SNRs smaller than 3.2 dB and MAP3 for SNRs greater than this value (we call this technique adaptive symbol mapping).
A comparison between the combinations MAP3 mapping/(1,7) constellation and SSP mapping/Conventional 8-PSK constellation were carried out and its result is given in Figure 4. This figure shows that the first com-

Figure 3. The BICM-ID’s BER performance for all used mappings (for (1,7) constellation) after 8 iterations.

Figure 4. A comparison between the performances of the system using the two combinations.
bination gives a very significant gain compared to the second combination and this is from the 1st to the 8th iteration.
It is necessary to note that the 1st combination, with only 4 iterations, gives better performance than the 2nd combination with 8 iterations. For example, a gain of 4 dB (4.5 dB respectively) is given by iteration 4 (iteration 8 respectively) of the 1st combination compared to iterations 4 and 8 of the 2nd combination at a BER level equal to 10−5, and they (iterations 4 and 8 of the first combination) can attain a BER equal to 10−7 for a SNR = 5.6 dB.
For further results on the performance of (1,7) constellation and these used mappings reader can refer to Appendix.
5. Conclusion
This paper proposes MAP3 as a very suitable mapping for (1,7) constellation, and shows that the new combination MAP3/(1,7) constellation significantly outperforms the well-known combination SSP mapping/conventional 8-PSK constellation.
REFERENCES
- G. Ungerboeck, “Channel Coding with Multilevel/Phase Signals,” IEEE Transactions on Information Theory, Vol. IT-28, 1992, pp. 55-67.
- E. Zehavi, “8-PSK Trellis Codes for a Rayleigh Fading Channel,” IEEE Transactions on Communications, Vol. 40, No. 5, 1992, pp. 873-883. doi:10.1109/26.141453
- G. Caire, G. Taricco and E. Biglieri, “Bit Interleaved Coded Modulation,” IEEE Transactions on Information Theory, Vol. 44, No. 3, 1998, pp. 927-946. doi:10.1109/18.669123
- C. E. Sundberg and N. Seshadri, “Coded Modulations for Fading Channels: An Overview,” European Transactions on Telecommunication, Vol. 4, No. 3, 1993, pp. 309-324. doi:10.1002/ett.4460040311
- C. Berrou and A. Glavieux, “Near Optimum Error-Correcting Coding and Decoding,” IEEE Transactions on Communications, Vol. 44, No. 10, 1996, pp. 1261-1271. doi:10.1109/26.539767
- X. Li and J. A. Ritcey, “Bit Interleaved Coded Modulation with Iterative Decoding,” IEEE Communications Letters, Vol. 1, No. 6, 1997, pp. 169-171. doi:10.1109/4234.649929
- X. Li, A. Chindapol and J. A. Ritcey, “Bit Interleaved Coded Modulation with Iterative Decoding and 8PSK Signaling,” IEEE Transactions on Communications, Vol. 50, No. 8, 2002, pp. 1250-1257. doi:10.1109/TCOMM.2002.801524
- N. S. Muhammad and J. Speidel, “Joint Optimization of Signal Constellation and Bit Labeling for Bit Interleaved Coded Modulation with Iterative Decoding,” IEEE Communications Letters, Vol. 9, No. 9, 2005, pp. 775-777.
- J. Tan and G. L. Stuber, “Analysis and Design of Symbol Mappers for Iteratively Decoded BICM,” IEEE Transactions on Wireless Communications, Vol. 4, No. 2, 2005, pp. 662-672. doi:10.1109/TWC.2004.842966
- S. Benmahmoud, A. Djebbari and A. Taleb-ahmed, “The Effects of Signal Mappings on the Performances of a BICM-ID System Based on 8PSK Constellation Operating over a Rayleigh Fading Channel,” Proceedings of the 2nd International Conference on Advanced Computer Theory and Engineering, Cairo, 25-27 September 2009.
- S. Benmahmoud and A. Djebbari, “Signal Mappings of Rectangular 8-QAM Constellation for BICM-ID Systems over an AWGN Channel,” Proceedings of the International Conference on Image, Signal Processing and their Applications, Mostaganem, 19-21 October 2009.
- S. Benmahmoud and A. Djebbari, “Seven Different 8-ary Constellations for BICM-ID,” Proceedings of the 9th International Conference on Electronics, Computer and Computation, Ankara, 1-3 November 2012.
Appendix
Figures 5-11 give the BER versus SNR curves for each mapping for (1,7) constellation for iterations 1 until 8.
The following simulation curves can be used for comparison purposes.

Figure 5. The BICM-ID’s BER performance with MAP1/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 6. The BICM-ID’s BER performance with MAP2/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 7. The BICM-ID’s BER performance with MAP3/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 8. The BICM-ID’s BER performance with MAP4/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 9. The BICM-ID’s BER performance with MAP5/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 10. The BICM-ID’s BER performance with MAP6/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

Figure 11. The BICM-ID’s BER performance with MAP7/ (1,7) constellation for iterations 1, 4, ∙∙∙, 8.

