Advances in Pure Mathematics
Vol.05 No.10(2015), Article ID:58739,3 pages
10.4236/apm.2015.510055
A Note on the Selection Expectation and Support Function
Rigao He
Department of Mathematics, College of Science, Hunan Institute of Engineering, Xiangtan, China
Email: rg@shu.edu.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2015; accepted 9 August 2015; published 12 August 2015
ABSTRACT
In this paper, we prove the relationship between selection expectation and support function by a new method.
Keywords:
Support Function, Hausdorff Metric, Random Set, Selection Expectation

1. Introduction
The studies of random geometrical objects can go back at least to the famous Buffon needle problem [1] . Then the theory of random sets first study in the book by Matheron [2] , who formulated the exact definition of a random closed set and developed the relevant techniques. The recently published book by Molchanov [1] is highly interdisciplinary and unites a number of mathematical theories and concepts for stochastic geometry, which has witnessed a rapid growth (see, e.g., [3] -[12] ).
The relationship between random sets and convex geometry has been thoroughly explored within the stochastic geometry literature; see, e.g. Weil and Wieacker [13] . The main techniques stem from convex and integral geometry; see Schneider [14] , Gardner [15] and Schneider and Weil [8] . The support function is one of the most important concepts in convex geometry. The goal of the present paper is to discuss a new approach for the relationship between selection expectation and support function, which has played an essential role in proving the strong law of large numbers for random compact sets [4] .
The organization of this manuscript is as follows. In the next section, we set notations and give preliminaries. In the last section we will prove the relationship between selection expectation and support function by a new method.
2. Notations and Preliminaries
We consider the d-dimensional Euclidean space 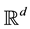 equipped with its usual inner product
equipped with its usual inner product , norm
, norm , the unit sphere
, the unit sphere  and the unit ball B.
and the unit ball B.
Let 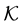 denote the family of all nonempty, compact subsets of
denote the family of all nonempty, compact subsets of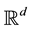 ,
, 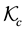 denote the subfamily of
denote the subfamily of  which are also convex.
which are also convex.
For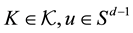 , the support function [14] [15] of K is defined by
, the support function [14] [15] of K is defined by
 (1)
(1)
Obviously, for K,  ,
,
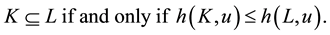
Hence a convex body is uniquely determined by its support function.
In order to show that a sequence of the sets of nonempty, compact subsets converges to another set of nonempty, compact subsets. One must define the distance between two sets. It motivates the following definition.
For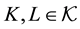 , Hausdorff metric (Hausdorff distance) [14] [15] between K and L is defined as
, Hausdorff metric (Hausdorff distance) [14] [15] between K and L is defined as
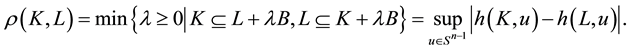 (2)
(2)
Then 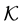 turns into a separable, locally compact metric space.
turns into a separable, locally compact metric space.
The point 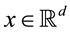 is a convex combination [14] [15] of the points
is a convex combination [14] [15] of the points

The set of all convex combinations of any finitely many elements of A is called the convex hull of A and is denoted by coA.
The family of closed subsets of 


A map 


It is natural to define random open sets as complements to random closed sets, so that 

Therefore we can regard a random set X as a measurable map defined on an abstract probability space 

A random set X is called simple, if there exists a finite measurable partition 



A random set X is called approximable if X is an almost sure limit of a sequence of simple random sets.
Similarly, a random set X with almost surely compact values is called a random compact set.
The norm 


A random vector 








The space 

Following Artstein and Vitale [4] in adapting the Aumann [16] integral, the expectation of X is defined by

Remark: 1) Selection expectation (also called the Aumann expectation), which is the best investigated concept of expectation for random sets. Since many results can be naturally formulated for random closed sets in Banach spaces.
2) We cite an example to illustrate the meaning of selection expectation. If X is a simple random compact set, i.e. 



3) 
4) Moreover, if the probability space 

3. Selection Expectation and Support Functions
Now we are ready to prove the main result in this section.
Theorem ([1] , p. 159, Theorem 1.26). If 

Proof. One of two probability spaces contains the atoms which may lead to the fact that two independent and identically distributed random compact sets may have different selection expectations. Therefore if 
Note that if X is a random compact set, then 
For

Let 



It follows that

Acknowledgements
The authors would like to acknowledge the support from the Educational Commission of Hunan Province of China (12A033) and the Hunan Provinial Natural Science Foundation of China (14JJ2122).
Cite this paper
RigaoHe, (2015) A Note on the Selection Expectation and Support Function. Advances in Pure Mathematics,05,583-586. doi: 10.4236/apm.2015.510055
References
- 1. Molchanov, I.S. (2005) Theory of Random Sets. Springer, London.
- 2. Matheron, G. (1975) Random Sets and Integral Geometry. Wiley, New York.
- 3. Artstein, Z. (1974) On the Calculus of Set-Valued Functions. Indiana University Mathematics Journal, 24, 433-441.
http://dx.doi.org/10.1512/iumj.1975.24.24034 - 4. Artstein, Z. and Vitale, R.A. (1975) A Strong Law of Large Numbers for Random Compact Sets. Annals of Probability, 5, 879-882.
http://dx.doi.org/10.1214/aop/1176996275 - 5. Cressie, N. (1978) A Strong Limit Theorem for Random Sets. Advances in Applied Probability, 10, 36-46.
http://dx.doi.org/10.2307/1427005 - 6. Kendall, D.G. (1974) Foundations of a Theory of Random Sets. In: Harding, E.F. and Kendall, D.G., Eds., Stochastic Geometry, Wiley, New York.
- 7. Puri, M.L. and Ralescu, D.A. (1983) Strong Law of Large Numbers for Banach Space Valued Random Sets. Annals of Probability, 1, 222-224.
http://dx.doi.org/10.1214/aop/1176993671 - 8. Schneider, R. and Weil, W. (2000) Stochastische Geometrie. Teubner, Leipzig.
http://dx.doi.org/10.1007/978-3-322-80106-7 - 9. Vitale, R.A. (1990) The Brunn-Minkowski Inequality for Random Sets. Journal of Multivariate Analysis, 33, 286-293.
http://dx.doi.org/10.1016/0047-259X(90)90052-J - 10. Vitale, R.A. (1991) Expected Absolute Random Determinants and Zonoids. Annals of Applied Probability, 1, 293-300.
http://dx.doi.org/10.1214/aoap/1177005938 - 11. Vitale, R.A. (1995) On the Volume of Parallel Bodies: A Probabilistic Derivation of the Steiner Formula. Advances in Applied Probability, 27, 97-101.
http://dx.doi.org/10.2307/1428098 - 12. Vitale, R.A. (1996) The Wills Functional and Gaussian Processes. Annals of Probability, 24, 2172-2178.
http://dx.doi.org/10.1214/aop/1041903224 - 13. Weil, W. and Wteacker, J.A. (1993) Stochastic Geometry. In: Gruber, P.M. and Wills, J.M., Eds., Handbook of Convex Geometry, Elsevier Sci. Publ., North-Holland, 1393-1438.
http://dx.doi.org/10.1016/b978-0-444-89597-4.50023-8 - 14. Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511526282 - 15. Gardner, R.J. (1995) Geometric Tomography. Cambridge University Press, Cambridge.
- 16. Aumann, R.J. (1965) Integrals of Set-Valued Functions. Journal of Mathematical Analysis and Applications, 12, 1-12.
http://dx.doi.org/10.1016/0022-247X(65)90049-1







