Optimal Entry and Exit Strategy under Uncertainty with Stochastic Volatility ()
1. Introduction
In the real world, most investment decisions are made in an uncertain background and are costly to reverse in the future. Such as firms enter and exit foreign markets in responding to real exchange rate fluctuations. And corporations decide whether to initiate new or terminate existing products based on uncertain profitability prospects of these actions. There are many other similar examples can be offered, but we won’t enumerate them one by one here in order to free from repeating. In view of these facts, a number of investment models have been studied within stochastic calculus framework in the past decades. Nowadays, the interest has been motivated and great progresses have been made in this field due to the recent advances in the theory of mathematical finance and of stochastic optimal control. Absolutely, considerable results have been obtained.
Usually, industries often go through successive phases of entry and exit with the change of economic environment. For example, excess entry may be observed when the market demand is unknown and a wave of exit is expected to follow. Moreover, there may be exit by either too many or too few firms because demand uncertainty is not completely resolved, then in this case, a new wave of entry or exit respectively will follow in turn. It’s well known that much work on investment, specifically that exploits an analogy between real and financial investment decisions, which known as “real options” approach has been done before. In this paper, however, we still present a dynamic model of entry and exit under price uncertainty to establish optimum time for entry and exit as strategic decisions for a firm, decisions that can be modeled through real options.
We begin by making an overview as well as stating the relation of this paper to some recent literature on this topic. Eriksson [1] presented a dynamic model of industry equilibrium to show how growth, entry and exit of firms are interrelated. The results demonstrate that simultaneous occurrence of entry and exit can be explained formally by taking into account the fact that every firm’s profitability to some degree is subject to random shocks, and prove that industry growth comes mainly from existing firms. Under the condition that output price follows a random walk, Dixit [2] examined a firm’s entry and exit decisions. The paper finds there exists a pair of trigger prices for entry and exit, where entry trigger price exceeds the variable cost plus the interest on the entry cost, while the exit trigger one is less than the variable cost minus the interest on the exit cost. A dynamic stochastic model for a competitive industry which endogenously determines processes for entry and exit and for individual firm’s output and employment was developed and analyzed in Hopenhayn [3]. The author presents conditions under which there will be entry and exit in the stationary equilibrium by extending long run industry equilibrium theory to account for entry, exit, and heterogeneity in the size and growth rate of firms. Also, entry and exit are part of the limiting behavior of the industry and not only part of the adjustment to a steady state is showed. The interlinked nature of decisions is shown to be essential even in the deterministic limit in Kongsted [4] by establishing the general deterministic limit that corresponds to Dixit’s model of entry and exit decisions under uncertainty. The limiting case, we mention that, without uncertainty may be interesting in itself, and is helpful in explaining numerical results appearing in literature regarding the volatility of price process. Applying a dynamic model of intertemporal entry and exit in perfectly competitive markets with demand uncertainty and Bayesian learning, Vettas [5] not only presented a unique equilibrium path characterized by a pair of simple zero-expected profit equations, but also suggested there are waves of entry and exit, and firms operate under uncertainty during each of these phases. Duckworth and Zervos [6] considered an investment model involves entry and exit decisions as well as decisions related to production scheduling, which is a generalization to many models that have been studied in previous literature. Using stochastic dynamic programming approach, one closed form analytic solution that can take qualitatively different forms depending on parameter values is obtained.
In the past decade, many researchers spent much time and energy to investigate this area from different aspects, and a number of new and useful results have been achieved. Within these papers, Amir and Lambson [7] constructed an infinite-horizon, stochastic model of entry and exit with sunk costs and imperfect competition. They find that for the general dynamic stochastic game, there exists a sub-game perfect Nash equilibrium as a limit of finite-horizon equilibria, which has a relatively simple structure characterized by two numbers per finite history. And relative to a social optimum, it tends to exhibit excessive entry and insufficient exit under very general conditions. Considering the exported-oriented manufacturer with risk neutrality and rational expectation to make decisions to switch production location freely between domestic and foreign ones, Lin and Wu [8] extended the build to order production model under uncertainty of exchange rate. The paper claims that the optimal entry and exit critical points of Cobb-Douglas production function are equal no matter using real options or net present value method as long as both the cost of production transferring and the drift of real exchange rate are zero. Therefore, no matter where the production locations are, export-oriented manufacturer can make decisions at the optimal critical value. Further, another way of thinking for export-oriented manufacturer is provided. Entry and exit decisions under price uncertainty are discussed in Sødal [9] using a discount factor approach to investment, by which the firm’s value can be expressed as a function of a set of trigger prices at which investment takes place and the optimal policy can be determined by simple maximization. The paper, which based on the model proposed in Dixit’s, expands to construction and scrapping decisions, investment lags, diminishing production capacity, and limits to the number of lay-up periods. Under uncertainty and through a project analyzed by a company from furniture industry, Vintila [10] suggested that entry in the market takes place when total cost is much lower than price level, whereas strategy to exit from the market is adopted when variable cost is much higher than price level. In addition, the effect of this phenomenon is examined by changing model’s parameters. Hanazono and Yang [11] discussed the dynamics of entry and exit based on firm’s learning about its relative cost positions. They claim that firms with relatively lower costs are viable in the long-run since market demand only accommodate a fraction of firms to operate, while some firms will exit from market if excessive entry occurs. Besides, the unique symmetric sequential equilibrium, whose properties are in line with empirical observations is derived. That is, with lower cost firms entering earlier than higher cost ones, entry occurs gradually, and exiting firms are among the ones that entered later. Meanwhile, equilibrium overshooting probability is always positive but decreasing over time. O’Brien and Folta [12] examined whether the option value of keeping an operation alive will deter firms from exiting an industry. They found that uncertainty dissuades firms from exiting an industry, but only when the sunk costs of entering and exiting that industry are sizeable. Furthermore, sunk costs can be influenced by the technological intensity of an industry, by the extent to which a firm competes on the basis of innovation, and by the firm’s diversification strategy has been argued and shown. A firm’s entry and exit decisions are examined in Tsekrekos [13] under the assumption that the output equilibrium price follows an exogenous mean reverting process. The paper finds that mean reversion has significant effects both on firm-specific entry and exit decisions and on the balance of entering and exiting firms in an industry. Thus, use the more tractable GBM process in models of aggregate industry investment as an approximation for the mean-reverting process would be improper.
As we all know, firms in developing industries decide whether and when to enter the market depending on the state of demand, existing firms in the industry, and the firm’s capabilities. Thus, a model of increasing demand, in which firms decide when to enter the market anticipating the strategic behavior of other potential entrants, and the effects of entry on future potential entrants has been examined in Shen and Villas-Boas [14]. They proved that the ability of early entry to defer future competitor’s entry leads firms to enter the market at a rate faster than demand is expanding. Generally, if there is the potential for many firms to enter the market, then firms may be less likely to enter due to future competitor entry to correct any market opportunities. While firms end up entering the market at a faster rate in the early periods if they enter the market depending on their fixed capabilities rather than depending on the firm’s circumstances at each moment in time. Recently, Piccolo [15] proved that if entry is relatively more costly than monitoring, then the equilibrium number of firms decreases with uncertainty in a model of competing managerial firms. Introducing idiosyncratic firm efficiency shocks into a continuous-time general equilibrium model of trade with heterogeneous firms proposed by Impullitti et al. [16], they points that hysteresis in export market participation will rises in the presence of sunk costs of export entry and uncertain efficiencies. For one thing, once a firm achieves a given size, then it will enter into the export market to reflect its efficiency, but may keep exporting even if its efficiency falls below the initial entry level. For another thing, unlike other firms that never enter into the foreign market, some exporters won’t sell as much as them in the domestic market. We mention that the qualitative features of firm birth, growth, export market entry and exit, and death are all captured in this model. Simultaneously, reduction in sunk costs as opposed to overhead costs matters for a firm’s selection and persistence in export status is shown. Specifically, by reducing sunk costs of export entry, trade liberalization reduces a firm’s export status persistence, while by reducing costs of overhead export, the opposite happens when liberalization takes place. Regarding more research papers about this topic, one can refer to Campa [17], Murto [18], Jellal [19], Bayer [20], Miller [21], Kwon [22] and the references therein.
In the end, we mention that the problem we study in this paper has various applications in many aspects. One potential application, for instance, appears in the area of valuating off-shore petroleum leases, and specially in pricing the right to exploit an oilfield with given reserves. And the other application occurs in the field of valuating “know-how”. Further, by modifying the model framework slightly, one can apply to the analysis of decisions to buy or scrap a durable consumption good, to hire or fire labor and so forth. In view of this point, we will use the analysis of decisions to study a modified model that differs from the previous literatures.
The contribution of this paper is that we make a generalization to previous papers such as Dixit and Tsekrekos, which are two standard model to study entry and exit decisions under uncertainty. The difference between ours and theirs is that we depict uncertainty by Heston-GBM, rather than conventional GBM or MR. In other words, we replace constant volatility in their settings by allowing volatility process itself to be stochastic. More specifically, we assume the instantaneous variance in the price follows a Cox-Ingersoll-Ross process, which is often referred to as Heston stochastic volatility in the theory of option pricing under stochastic volatility. Nevertheless, our improvements are not just by using complicated and profound mathematical knowledge to examine or repeat one commonplace topic. The study shows that the extension and generalization have theoretical significance and application value as well. What’s more important, the results we obtained are not only consistent with our anticipation, but also in line with some economic phenomena in reality, and further can make new interpretations to them from different perspective. Of course, the problem presented in this paper is still an open topic, so far to our knowledge.
The remainder of this paper is organized as follows. We first introduce the model at length in Section 2. Then in Section 3, we solve and analyze the model. Subsequently, we illustrate numerical simulations in Section 4. Lastly, Section 5 concludes the results.
2. Model Setup
In this section, we will introduce our model in detail for the sake of intactness though it is an extension to the standard models to study entry and exit decisions under uncertainty, which proposed by Dixit and Tsekrekos.
A firm possesses an exclusive production technology and consider to enter some market by making a fixed scale investment of one lump sum entry cost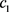
. Once the firm become active in the market, then it can produce a unit flow of output at variable cost v. Alternatively, the firm can choose to suspend operations at any point by spending one lump sum exit cost
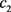. Certainly, it must incur the entry cost 
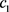again should it decide to reenter at some future time. In addition, we denote by r the risk-free interest rate or discount rate. By the way, 
, 
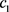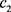, v and r are all constant and positive variables.
The uncertainty originates from the output price P, which evolves exogenously to the firm. Namely, the firm is a price-taker. Unlike Dixit and Tsekrekos suppose the price P therein follows classical GBM or MR process, we suppose the price P herein follows a Heston-GBM process. According to Heston [23], the Heston-GBM process can be depicted as
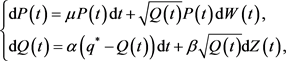
Here,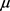 
is the drift rate of price process
, 
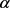is the mean reverting rate, 
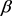is the volatility, 
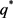is the long-run mean level of variance process
, 
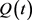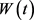and 
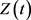are two correlated standard Brownian motions with correlation coefficient
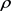. Besides, 
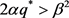is required to make 
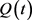strictly positive, and 
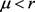is needed to guarantee convergence.
The firm is assumed to be risk-neutral as well as competitive, and its objective is to maximize the expected net present value. Clearly, its strategy problem has three state variables, one is the current price P, one is current variance Q, and the other is a discrete variable that indicates the firm is active or inactive. This setting, in some sense, corresponding to the firm possess a call-option to enter the market when it is inactive, and a put-option to exit when it is active. The two options must be valued at the same time because they are interlinked by exercising one the firm acquires the other.
Again, we emphasize that suppose the price follows Heston-GBM not to just apply complicated and profound mathematical knowledge to make the framework hard to understand, but because the following reasons such as: 1) Stochastic volatility, for one thing, can explain many empirical findings like “Volatility Clusters” observed in financial markets, and for another thing, can replicate the observed “Volatility Smile” and thereby is essential for pricing and hedging financial derivatives; 2) In the form of implied volatility, further proof shows that constant volatility hypothesis in Black-Scholes framework is not realistic; 3) The necessity of including stochastic volatility into a real option model is strongly indicated by commercial property literature; 4) Whenever changes in surrounding economic environment affect the level of fluctuations in project value, then stochastic volatility will undoubtedly be relevant for the timing of investment project; 5) So far as we know, the issue of entry and exit strategies under uncertainty has not been referred in stochastic volatility setting.
As we mentioned, the risk neutral and competitive firm has two discrete states, idle or active. When the firm’s state is idle, then it decides whether to keep idle or to enter. Likewise, when the firm’s state is active, then it decides whether to keep active or to exit. Thus, the decision problem of the firm is to switch optimally from one state to the other state. For explicitness, we denote by ![]()
and ![]()
respectively the expected net present value of the firm with initial price P as well as variance Q in the idle and in the active state, and follows optimal entry-exit strategies. In the sequel, we will construct the Heston-GBM model at length.
Entry Problem. We assume an idle firm starts at time 0 with current price P as well as variance Q, and choose to enter into the market at time t. Then it must pays one lump-sum entry cost![]()
, and further its value switches to ![]()
. Therefore
![]()
where E is the symbol of expectation operator.
We point that if the idle firm keeps its state, then it will not has any other profit besides its expected capital gain![]()
, which must be equal to![]()
. According to Heston [23], it’s not difficult to demonstrate that ![]()
satisfies the following partial differential equation (Hereafter PDE)
![]()
(1)
with boundary condition
![]()
(2)
and value-matching condition
![]()
(3)
smooth-pasting condition
![]()
(4)
Here, ![]()
is a trigger price such that staying idle is optimal on an interval to its left side (i.e.![]()
) while becoming active is optimal on an interval to its right side (i.e.![]()
). Notice that boundary condition (2) ensures that an idle firm’s entry to a market will be worthless as output price becomes very small.
Exit Problem. We assume an active firm starts at time 0 with current price P as well as variance Q, and choose to exit from the market at time t. Then it must pays one lump-sum exit cost ![]()
and has a cash flow of ![]()
for any instant![]()
, and its value switches to ![]()
at time t. Therefore
![]()
Similar to the computation of Equation (1), there yields the following PDE
![]()
(5)
with boundary condition
![]()
(6)
and value-matching condition
![]()
(7)
smooth-pasting condition
![]()
(8)
Here, ![]()
is another trigger price such that keeping active is optimal on an interval to its right side (i.e.![]()
) while becoming idle is optimal on an interval to its left side (i.e.![]()
). Notice that boundary condition (6) implies that an active firm’s exit from a market will be worthless as output price becomes very high, and at the same time guarantees that firm’s value converges to the expected net present value of operating in the market forever, come what may, starting from an initial price P. That is, it rules out explosive growth of firm’s value with high output price.
Remark 1. As proposed in Dixit’s, ![]()
is the trigger price for entry while ![]()
is the trigger price for exit, and![]()
. Put differently, an idle firm will enter into the market if![]()
, and an active firm will exit from the market if![]()
. However, if the price locates between ![]()
and![]()
, then for the active firm, it’s optimal to keep production activity, but for the idle firm, it’s optimal to continue being inactive.
3. Model Analysis
Now, we try to solve the two PDEs shown in (1)-(2) and (5)-(6), respectively. For our purpose, we rewrite PDE (1) into compact form as
![]()
where
![]()
![]()
![]()
![]()
Then we can expand ![]()
as
![]()
Keeping terms up to![]()
, then the compact form of PDE (1) can be changed into
![]()
To determine functions![]()
, we next equate various order of![]()
.
Adopting the approaches presented in Ting et al. [24], and proceeding step by step with slight modification, we get the asymptotic solutions of ![]()
and ![]()
are
![]()
(9)
![]()
(10)
since ![]()
is a special solution for PDE (5). Here ![]()
and ![]()
are two undetermined parameters, and
![]()
(11)
![]()
(12)
which are the two roots of quadratic equation
![]()
Remark 2. The argument processes of solutions ![]()
and ![]()
are very similar to Ting et al. [24], thus we leave out the details for the sake of avoiding wordiness. Besides, ![]()
and ![]()
due to ![]()
and the convexity of![]()
, which guarantee the two boundary conditions (2) and (6) for PDEs (1) and (5), respectively.
Remark 3. The solution ![]()
must be non-negative in order to possess economic meanings, so![]()
. Similarly, ![]()
because the yields of an active firm from the optimal strategy should equal to or more than the expected
value of ![]()
from the feasible strategy of operating forever.
Recalling value-matching condition and smooth-pasting condition (3)-(4) for ![]()
and (5)-(6) for![]()
, we have
![]()
(13)
![]()
(14)
![]()
(15)
![]()
(16)
Obviously, ![]()
and![]()
, ![]()
and ![]()
are determined by Equations (13)-(16). However, it’s difficult to derive the expressions of trigger prices ![]()
and ![]()
because all equations with respect to them are transcendental equations. Thus, we need to make some qualitative analysis to obtain some important properties of them. Such as neither ![]()
goes to infinity nor ![]()
goes to infinitesimal, because the exit of an active firm is worthless when the output price rises to![]()
, and the entry of an idle firm is worthless when the output price falls to![]()
. Further, to this end, we claim that ![]()
goes to zero in (13)-(14) if the exit cost goes to infinity and ![]()
goes to zero in (15)-(16) if the entry cost goes to infinity. Then we get
![]()
(17)
![]()
(18)
Although the analytical expressions of the two trigger prices cannot be derived from Equations (17) and (18), we can verify that there holds![]()
, ![]()
, where![]()
, ![]()
are the Marshallian trigger prices, by employing the method presented in Dixit’s with slight modification. This means uncertainty from volatility widens Marshallian range ![]()
of inaction. Particularly, if![]()
, then![]()
, thus the active firm will never exit from the market. As to more analytical properties, we refer to the numerical simulations in the subsequent section.
Remark 4. When the variance process ![]()
is constant, and set to be![]()
. Then![]()
, and![]()
. Under this condition, our Heston-GBM model in this paper collapse into the GBM model in Dixit’s. And it’s not difficult to verify that the trigger prices ![]()
in Equations (17)-(18) can be solved as the same as Dixit [2].
4. Numerical Simulation
In this section, we investigate the analytical properties for trigger prices by numerical simulation. Specifically, we focus on the effects of the drift rate ![]()
of price process![]()
, the mean reverting rate![]()
, the long-run mean level ![]()
and the volatility ![]()
of variance process ![]()
on the trigger prices ![]()
and![]()
, respectively. For our purpose, ![]()
, ![]()
, ![]()
and ![]()
are predetermined. In the sequel, we demonstrate our numerical results one after one from Tables 1-4.
From Table 1, it’s easy to see that both ![]()
and ![]()
are decreasing with![]()
, for any![]()
. That is, the drift rate of the price process has negative effects on the trigger prices. The intuition is that a firm will enter the market at a lower threshold if it expects a favorable price trend, and once enters in, it’s more willing to hang on even if a temporarily adverse price appears. Notice that the trigger prices illustrated in the case ![]()
are actually equivalent to which derived directly from Dixit’s GBM model because ![]()
are both equal to zero and the trigger prices ![]()
expressed in Equations (17)-(18) can be solved explicitly as the same as Dixit’s. By simple computation, we find that for every fixed ![]()
such as 1, 0, or −0.5, the width of the range of inaction, namely the difference between ![]()
and![]()
, is decreasing with the drift rate ![]()
of price process. That is, the drift rate of price process has negative effects on width of the inaction range no matter for GBM model with constant volatility or for Heston-GBM model with stochastic volatility.
![]()
Table 1. The effects of drift rate of price process on trigger prices.
Following Table 2, we know that an increase in ![]()
reduces the trigger prices in the case![]()
, but raises the trigger prices in the case![]()
. That is, the mean revering rate of variance process has negative effects on trigger prices when![]()
, but has positive effects on trigger prices when![]()
. The logic is that the larger the mean reverting rate of variance process, the shorter the time that the stochastic variance of price process keeps far away from the long-run mean level. This means that the price neither stays at a very high level nor at a very low level for a long time. Thus, when![]()
, the idle firm would reduce entry price in order to enter the market while the active firm would reduce exit price in order not to exit from the market for pursuing gain; when![]()
, the idle firm would raise entry price in order not to enter the market while the active firm would raise exit price in order to exit from the market for preventing loss. In addition, we can check that the width of the range of inaction is decreasing (increasing) with the mean reverting rate of variance process in the case ![]()
(![]()
). Regarding the case![]()
, it’s unsurprising to see the trigger prices do not change with the mean reverting rate of variance process and so does the width of the inaction range. This is because the trigger prices derived in the case ![]()
are independent of the mean reverting rate of variance process.
![]()
Table 2. The effects of mean reverting rate of variance process on trigger prices.
In terms of Table 3, we see that the entry price is increasing, whereas the exit price is decreasing with the long-run mean level of variance process, for any![]()
. The reason is that higher long-run mean level of variance process implies bigger stochastic volatility of price process, thus the idle firm will enter the market at a higher threshold, but the active firm will not exit from the market even though a suddenly adverse price emerges, which reflects the significance of hysteresis. We mention that the result is in line with Dixit’s as well as Tsekrekos’s, and thereby, the finding is robust no matter the volatility of price process is constant or stochastic. Similarly, we point that for any constant![]()
, the long-run mean level of variance process broadens the width of the range of inaction regardless the framework is GBM and MR with constant volatility or is Heston-GBM with stochastic volatility.
![]()
Table 3. The effects of long-run mean level of variance process on trigger prices.
According to Table 4, we know that an increase in ![]()
raises the trigger prices in the case![]()
, but reduces the trigger prices in the case![]()
. That is, the volatility of variance process has positive effects on trigger prices when![]()
, but has negative effects on trigger prices when![]()
. The sense is that larger volatility of variance process induces indirectly larger volatility of price process when ![]()
while smaller volatility of price process when![]()
. Therefore, in the case![]()
, with the increasing of the volatility of variance process, the idle firm will raise the entry threshold to enter the market discreetly, and the active firm will raise the exit threshold to prevent exiting from the market easily. While in the case![]()
, the opposite result occurs. Besides, we can verify that the width of the range of inaction is increasing(decreasing) with the volatility of variance process in the case ![]()
(![]()
). Analogously, regarding the case![]()
, it’s expectable to see the trigger prices do not vary with the volatility of variance process and so does the width of the inaction range. This is also because the trigger prices derived in the case ![]()
do not dependent on the volatility of variance process. Further, that is why the trigger prices illustrated in Table 2 and Table 4 are the same under the condition ![]()
with the same drift rate of price process and long-run mean level of variance process.
![]()
Table 4. The effects of volatility of variance process on trigger prices.
Finally, throughout Tables 1-4, it’s not difficult to find two common places, no matter for GBM model with constant volatility or for Heston-GBM model with stochastic volatility. The one is our numerical results confirmed that uncertainty would widen Marshallian range of inaction, namely ![]()
(Under our assumption,![]()
). The other one is the trigger prices and the width of inaction range from Heston-GBM model with stochastic volatility are relatively bigger when ![]()
while are relatively smaller when![]()
, comparing to the counterparts from GBM model with constant volatility and for each given drift rate of price process, or mean reverting rate, or long-run mean level, or volatility of variance process. Put differently, relative to constant volatility, stochastic volatility has significantly positive or negative effects on the trigger prices and the width of inaction range, which depends on the correlation of the two Brownian motions in price process and variance process, respectively.
5. Conclusions
In the past decades, many investment decisions of firms such as when to invest in an emerging market or whether to expand the capacity have been studied by many researches, which involve irreversible investment and uncertainty about demand, cost or competition, etc. Naturally, considerable results and conclusions have been achieved. In spite of this, there still exist some issues that can be studied further. In view of this point, a model of optimal inertia in investment decisions under uncertainty with stochastic volatility is established in this paper to deepen understanding of the issue and open up the way for treating further problems of this topic.
Unsurprisingly, our conclusions show that stochastic volatility undoubtedly be relevant for the timing of investment decisions. For Heston-GBM model, as demonstrated in the previous section, the change of the drift rate of price process plays negative role in trigger prices for any given![]()
. For any fixed![]()
, the effects of the long-run mean level of variance process on entry price are positive, whereas the effects on exit price are negative. We mention that the two findings above are robust no matter the volatility is constant or stochastic. The change of mean reverting rate of variance process has negative impacts on trigger prices when![]()
, while the change has positive impacts on trigger prices when![]()
. On the contrary, the effects of the volatility of variance process on trigger prices are positive when![]()
, while the effects are negative when![]()
. Comparing to trigger prices derived from GBM model with constant volatility, which are those illustrated in the case![]()
, the counterparts derived from Heston-GBM model with stochastic volatility are greater in the case ![]()
but smaller in the case![]()
. Namely, stochastic volatility has significantly positive or negative influence on trigger prices, relative to constant volatility. What’s more important, no matter the volatility is constant or stochastic, the uncertainty would widen the Marshallian range of inaction.
The major contribution of this paper is that we study a classical and hot topic from a new perspective. Unlike previous literatures, we here construct one stochastic volatility models, Heston-GBM, to study firm’s entry and exit strategy under uncertainty. The findings show that stochastic volatility has potent and significant impacts on firm’s investment decisions, which implies that we replace constant volatility by stochastic volatility not to apply profound mathematical knowledge to make the problem complicated, but to say the conventional GBM and MR process is not always the most appropriate for some economic variables. Indeed, relatively speaking, stochastic volatility models are able to capture the so called “Leverage Effect”. In brief, our extension not only has theoretical significance, but also has application value.
Acknowledgements
The author would like to thank the anonymous referees for their helpful comments, which greatly improved the presentation of this paper. The author also would like to thank the editors for their help.