On the Theory of Fractional Order Differential Games of Pursuit

Mashrabjan Mamatov¹, Durdimurod Durdiev², Khakim Alimov³

¹National University of Uzbekistan, Tashkent, Uzbekistan.
²Bukhara State University, Bukhara, Uzbekistan.
³Samarkand State University, Samarkand, Uzbekistan.

DOI: 10.4236/jamp.2016.48167                

Abstract

This article is devoted to studying of the problem of prosecution described by differential equations of a fractional order. It has received sufficient conditions of a possibility of completion of prosecution for such operated systems.

Keywords

Equations, Control Systems, Function, Derivative Kaputo

Received 15 July 2016; accepted 19 August 2016; published 22 August 2016

1. Introduction

The dynamics of the systems described by the equations of fractional order is the subject of research experts from around the middle of the XX century. The study of dynamical systems with fractional order management is actively developing in the last 5 - 8 years [1] [2] . The growing interest in these areas is due to two main factors. Firstly, by the middle of the last century it has been adequately worked out the mathematical foundations of fractional integro-differential calculus and the theory of differential equations of fractional order. Around the same time, it began to develop a methodology and application of fractional calculus in applications, and we started to develop numerical methods for calculating integrals and derivatives of fractional order. Secondly, in fundamental and applied physics by this time, it had accumulated a considerable amount of results, which showed the need for fractional calculus apparatus for an adequate description of a number of real systems and processes [3] . Examples of real systems will mention electrochemical cells, capacitors fractal electrodes, the viscoelastic medium. These systems have typically not trivial physical properties useful from a practical standpoint [4] - [7] . For example, the irregular structure of the electrodes in capacitors allows them to reach a much larger capacity, and the use of electrical circuits with elements having a transfer characteristic of fractional- power type, provides more flexible configuration of fractional order controllers used in modern control systems. For such control systems of fractional order as of today, there are no similar results Pontryagin type [8] - [11] .

2. Methods

Let driving of object in a finite-dimensional Euclidean space of 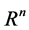be described by a differential equation of a fractional order of a look

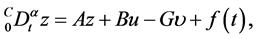(1)

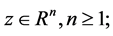
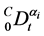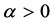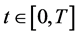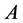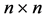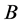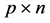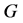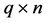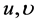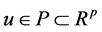where ―operator of fractional derivation, , ,―,―and―constant matrixes,―the operating parameters,―the operating parameter of the pursuing player, ,―the operating parameter of the running-away player, , and - compact, -known measurable vector function. We will understand a fractional derivative as left-side fractional derivative Kaputo [1] - [6] . Let’s remind that fractional derivative Kaputo of the random inappropriate order from function, is defined by expression

(2)

Besides in space the terminal set M is allocated. The running-away player seeks to place the aim of the pursuing player to bring z to a set M, to it. The problem of prosecution about rapprochement of a trajectory of the conflict operated system (1) with a terminal set M for terminating time from the standard initial positions is considered. Let’s say that differential game (1) can be finished from initial situation during if there is such measurable function that the solution of the equation

belongs to a set M at the time of at any measurable functions .

This work is dedicated to the receipt of sufficient conditions for the completion of the prosecution managed fractional order systems adjacent to the study [12] - [22] . Some results of this paper were announced at the International Labour Conference [16] [17] . In such a setting the pursuit problem was studied in [8] - [11] , but it was devoted to the study of control systems of the whole order. In this sense, this paper summarizes these works.

3. Results and Discussion

Let’s pass to the formulation of the main results. Everywhere further: 1) the terminal set M has an appearance, where the―linear subspace,―subset of a subspace of L―orthogonal addition; 2)―operator of orthogonal projection from on L; 3) operation is understood as operation of a geometrical subtraction [8] .

Let -matrix―an exponential curve [1] and

;

(3)

Theorem 1. If in game (1) at some, inclusion is carried out

(4)

That from initial situation is possible will finish prosecution during.

Let now the -arbitraries splitting a piece, и,

(5)

Theorem 2. If in game (1) at some, inclusion is carried out

(6)

That from initial situation is possible will finish prosecution during.

Let’s designate through set defined at all. Let’s consider

integral

(7)

Theorem 3. If in game (1) at some, inclusion is carried out

(8)

that from initial situation is possible will finish prosecution during.

Proof of the theorem 1. Two cases are possible: 1);. Case 1) trivial as at of inclusion (4) we have or that is equivalent to inclusion. Let now. After a

theorem condition, then there will be vectors and

such that (see (3), (4)). Further, according to determination of integral there is a summable function that.

Considering this equality, we will consider the equation

(9)

Relatively at fixed and. As, the equation (9) has the decision. We will choose the least in lexicographic sense from all solutions of the equation (9) and we will designate it through. Function, is lebegovsk measurable on and borelevsk measurable on [7] . Therefore for any measurable function, function, will be lebegovsk measurable function [7] . Let’s put and we will show that at such way of management of the parameter of u the trajectory gets on a set M in time, not surpassing.

Really, on (9) for the decision, the equation

we have ( [1] , p. 414)

As. Further we have. From here we will receive that. The theorem is proved completely.

Proof of the theorem 2. In view of a case triviality we will begin consideration with a case.

We have (see (5), (6)). is alternating integral with an

initial set [8] . Therefore for it semigroup property [4] is executed

(10)

where the―arbitraries positive fixed number;,the―arbitraries measurable function with values from Q.

Let―arbitrary measurable function. According to theorem conditions in an instant is known a narrowing, functions on a piece. Follows from inclusion (10) that for the arbitrary function, we have

(11)

Thus, for the arbitrary function, inclusion takes place (12). Therefore, at , inclusion is fair (12). From here existence of measurable function, such follows that and

(12)

Then

(13)

Further we argue similarly. As

(14)

Let’s receive

(15)

For the arbitrary measurable function. Therefore, there is a measurable function, such that and

(16)

Follows from a ratio (16) that

(17)

etc. It is clear, that there is a natural number j it that: 1); 2) on the known function, where the narrowing of function, on a piece, will be the measurable function meeting a condition ((17))

(18)

But

(19)

Therefore ((18), (19))

(20)

Similarly on formulas (18), (19), (20) finally we receive

Thus, for any point we have, that is the trajectory, left a point, in an instant turns out M on a set. The theorem is proved completely.

Proof of the theorem 3. Owing to a condition of the theorem (8) we have . Therefore (7), there is such measurable function , that

(21)

Let arbitrary measurable function, by definition of subtraction operation we will receive

(22)

From here owing to a condition of measurability existence of the measurable functions defined on a piece follows and

(23)

We will determine function by the found measurable function

(24)

For the decision corresponding to functions we have (21)-(24)

From here, that is the trajectory which left a point in an instant turns out M on a set. The theorem is proved completely.

4. Conclusion

Summarizing the results, we conclude that the differential game of pursuit of fractional order (1), starting from the position can be completed in time, respectively. Thus, to solve the game problem kind of persecution (1), we used a derivative of fractional order Caputo, which is determined by the expression (2). Many (3) analogue of the so-called first integral Pontryagin, including (4) gives the first sufficient condition for the possibility of the persecution of the task. Many (5)―an analog of the second integral Pontryagin, inclusion (6) gives the second sufficient condition for the possibility of the persecution of the task. Lots (7)―analogue N. Satimova third method, and the inclusion (8) gives a sufficient condition for the third opportunity to end the game. In Theorems 1 - 3, we obtain sufficient conditions for the solution of relevant problems in this form.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kilbas, A., Srivastava, H. and Trujillo, J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam, p. 541.
[2]	Lakshmikantham, V., Leela, S. and Vasundhara, D.J. (2009) Theory of Fractional Dynamic Systems. Cambridge Academic Publishers, Cambridge, p. 176.
[3]	Monje, C.A., Chen, Y.Q., Vinagre, B.M., Xue, D. and Feliu, V. (2010) Fractional-Order Systems and Controls: Fundamentals and Applications. Springer-Verlag, London, p. 415. http://dx.doi.org/10.1007/978-1-84996-335-0
[4]	Caponetto, R., Dongola, G., Fortuna, L. and Petras, I. (2010) Fractional Order Systems. Modeling and Control Applications. World Scientific, Singapore, p. 178.
[5]	Agrawal, O.P. (2008) A Formulation and Numerical Scheme for Fractional Optimal Control Problems. Journal of Vibration and Control, 14, 1291-1299. http://dx.doi.org/10.1177/1077546307087451
[6]	Frederico, G.S.F. and Torres, D.F.M. (2008) Fractional Optimal Control in the Sense of Caputo and the Fractional Noethers Theorem. International Mathematical Forum, 3, 479-493.
[7]	Warga, J. (1972) Optimal Control of Differential and Functional Equations. Academic Press, New York, p. 531.
[8]	Pontreagin, L.S. (1980) Linear Differential Games of Pursuit. Sb. Math., 112, 307-330.
[9]	Pontryagin, L.S. and Mischenko, E.F. (1971) Zadacha ob uklonenii ot vstrechi v lineinykh differentsialnykh igrakh. Differential Equations, 7, 436-445.
[10]	Mishchenko, E.F. and Satimov, N.Y. (1983) The Problem of Deviation from an Encounter in the Critical Case. Differential Equations, 19, 220-229.
[11]	Satimov, N.Y. (1976) On a Way to Avoid Contact in Differential Games. Mat. Sb., 99, 380-393.
[12]	Satimov, N.Y. and Mamatov, M.Sh. (1990) On a Class of Linear Differential and Discrete Games between Groups of Pursuers and Evaders. Differential Equations, 26, 1541-1551.
[13]	Satimov, N.Y. and Tukhtasinov, M. (2005) On Some Game Problems in Controlled First-Order Evolutionary Equations. Differential Equations, 41, 1114-1121.
[14]	Mamatov, M.Sh. (2009) On the Theory of Differential Pursuit Games in Distributed Parameter Systems. Automatic Control and Computer Sciences, 43, 1-8.
[15]	Mamatov, M.Sh. and Alimov, H.N. (2013) Solution of the Problem of Persecution in Games Distributed Systems of Higher Order. Siberian Advances in Mathematics, Novosibirsk, T.16, 229-239.
[16]	Mamatov, M.Sh. and Alimov, H.N. (2016) By Solving the Problem of Harassment Described by Differential Equations of Fractional Order. In: Proceedings of the 7th International Scientific Conference on Theoretical and Applied Sciences in the USA, CIBUNET Publishing, New York, 6-10.
[17]	Mamatov, M.Sh. and Alimov, H.N. (2016) The Pursuit Problem Described by Differential Equations of Fractional Order. Proceedings of the 6th International Scientific Conference on European Applied Sciences: Challenges and Solutions, ORT Publishing, Stuttgart, 14-18.
[18]	Mamatov, M.Sh., Tashmanov, E.B. and Alimov, H.N. (2013) Differential Games of Pursing in the Systems with Distributed Parameters and Geometrical Restrictions. American Journal of Computational Mathematics, 3, 56-61.
[19]	Mamatov, M.Sh., Tashmanov, E.B. and Alimov, H.N. (2015) Zwquasi-Linear Discrete Games of Pursuit Described by High Order Equation Systems. Automatic Control and Computer Sciences, 49, 148-152.
[20]	Mamatov, M.Sh. and Tukhtasinov, M. (2009) Pursuit Problem in Distributed Control Systems. Cybernetics and Systems Analysis, 45, 297-302.
[21]	Tukhtasinov, M. and Mamatov, M.Sh. (2008) On Pursuit Problems in Controlled Distributed Systems. Mathematical Notes, 84, 273-280.
[22]	Tukhtasinov, M. and Mamatov, M.Sh. (2009) About Transition Problems in Operated Systems. Differential Equations, 45, 1-6.