Phase Diagrams of the Semi-Infinite Blume-Capel Model with Mixed Spins (SA = 1 and SB = 3/2) by Migdal Kadanoff Renormalization Group ()
Received 19 January 2016; accepted 28 May 2016; published 31 May 2016
1. Introduction
The problems of surface magnetism have been investigated for many years. Among them the effects of surface on phase transitions in semi-infinite systems have received increasing interest. Real systems have surfaces, interfaces or boundaries and the translational symmetry is not preserved. This gives a set of surface phase diagrams richer than the infinite bulk one [1] - [4] . The simplest model is to assume that the surface is single planar, which defines the semi-infinite model.
Several experimental studies show a critical behaviour of the surface different than the bulk. As example, we mention the work done on mixed compounds NbSe2 [5] , NiO (111) [6] and Co/Ni (111) overlayers [7] , on which are observed surface and extraordinary phase transitions. In those cases, the surface has a critical temperature greater than the bulk. In other pure samples of Gd [8] , the surface and the bulk are at the same critical temperature, the transition is ordinary. The practice researches in magneto-electronic and materials using carriers based on spin properties instead of electrons and holes in traditional semiconductors are motivated by the development and application for information storage [9] and other applications in thermo-magnetic recording [10] . In the other hand, the theoretical studies of the critical surface effects have been developed during the last years, using a variety of approximations and mathematical techniques. An interesting literature review of the subject is in the work of K. Binder and Diehl [1] - [3] . The existence and critical behaviour of surface, extraordinary, special [11] [12] and extraordinary phase transitions have been illustrated using different approaches [2] [3] [13] - [16] , and various situations as pure, quenched and random systems at bulk or surface [17] - [20] have been studied. Also, the exact solution of the 2D semi-infinite Ising model has been proved [21] - [24] . The semi- infinite Blume-Capel model was also used to describe the wetting phenomenon. In reference [25] , the authors show that critical wetting in d = 2 is equivalent to a “bulk” critical phenomenon. A detailed study with a rich bibliography is found in reference [26] .
The three-dimensional semi-infinite spin-1 Ising model with a crystal field has been studied [27] . The spin-1 ferromagnetic Ising model with a crystal field has been introduced independently by Blume [28] and Capel [29] and is often called the Blume-Capel (BC) model. An extension of the BC model is the possibility of inclusion of higher spin values. Various types of phase diagram of a three-dimensional semi-infinite ferromagnetic spin-3/2 BC model were obtained within the framework both of the mean field theory and renormalization-group techniques [30] .
In the last years, a great attention has been devoted to systems of mixed spins and this is related to their importance in the study of magnetic materials with ferrimagnetic properties [31] . The system of mixed spins S = 1/2 and S = 1 has been one of the simplest to be studied early and largely, namely by the techniques of renormalization group [32] [33] , the Bethe-Peierls approximation [34] , the effective field theory [35] [36] , the Monte- Carlo simulation [37] [38] and the finite cluster approximation [39] .
Recently, this attention has been expanded on systems of mixed spins higher than 1/2, like the case S = 1 and S = 3/2, which has been also studied by several methods, as the mean field approximation (MF) [40] , the Bethe lattice recursion relations [41] [42] , the effective field theory [43] [44] , the Monte-Carlo simulation [45] , the Green’s function [46] , the recursion relations on Cayley tree [47] and the real space renormalization group theory [48] .
Our aim in this present paper is to determine the various types of phase diagram in the semi-infinite system of mixed spins S = 1 and S = 3/2 on the Blume-Capel model [28] [29] , which we study by using a renormalization group (RG) method, namely the Migdal-Kadanoff one [49] [50] , combining the decimation as well as the bond shifting. Our study focuses on the effect of two different single-ion anisotropies in the phase diagram of the mixed spin-1 and spin-3/2 Ising ferrimagnetic system. We organize our paper as follows. In Section 2, we treat the formalism of our method and we establish the Migdal-Kadanoff recursion equations. In Section 3, we present our results and discuss important points. Finally, we give our conclusion in Section 4.
2. Model and Method
2.1. Infinite Blume-Capel Model
We consider a two sublattice mixed spin-1 and spin-3/2 Blume-Capel model with different single-ion anisotropies ΔA and ΔB acting on the spin-1 and spin-3/2, respectively. The Hamiltonian of the system is given by
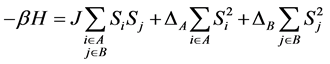(1)
where the sites of sublattice A are occupied by spins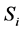
, which take the values of 
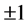and 0, while those of the sublattice B are occupied by spins
, which take the values of 
and
. J is the reduced bilinear exchange interaction and 
(with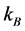 
the Boltzmann constant and T the absolute temperature). The first summation is over all nearest neighbor pairs of spins, the second and the third summations one over all sites.
In the Blume-Capel model, the reduced biquadratic interaction K is equal to zero, but we will take it into account due to the renormalization group technique we are using. We also introduce one additional interaction C to obtain self-consistent recursion relations. Thus, the Hamiltonian we will effectively use in the remainder of our work is as follows:
. (2)
The renormalization does not keep in general the parameters space of the Hamiltonian. The terms added to the original Blume-Capel Hamiltonian model, in addition to their role in the conservation of the parameter space, can be used in the improvement of critical exponents and precision Monte Carlo simulation: scaling correction [51] .
For example, in the Blume-Emery-Griffiths model, the three parameters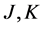 
and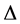 
are insufficient to stabilize the ferromagnetic phase which has been obtained by all the methods of effective fields.
To have a more reliable qualitative appreciation of the phase transitions characteristics, we use an approximation of the real space renormalization group, namely the Migdal-Kadanoff one, which combines decimation and bond shifting and is tractable in all space dimensionalities. In order to implement the renormalization machinery, we consider a one-dimensional chain (Figure 1) of four spins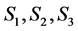 
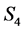and 
(
and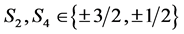 
), coupled by the interactions ![]()
and C.
The spatial factor rescaling, denoted by b, is chosen as an odd integer to keep the possible sublattice symmetry breaking character of the system. In our present study, we take![]()
. Furthermore, we have to take into account the coordination number of the site i in the crystal field term. With these considerations, we can write the reduced Hamiltonian of the four spins cluster as
![]()
(3)
After performing the decimation on the two middle spins ![]()
and![]()
, the previous chain becomes as shown in Figure 2. We obtain a two spins cluster described by the following reduced Hamiltonian![]()
:
![]()
(4)
with ![]()
and ![]()
the interactions after decimation and functions of ![]()
and the coordination number![]()
.
![]()
Figure 1. Chain of four spins, S1, S2, S3 and S4. J and K denote, respectively, the reduced bilinear and biquadratic interactions, while ∆i (i = A, B) is the crystal field at site i. Decimation will be performed on the two middle spins, S2 and S3.
By using the renormalization group equation, we can make the link between (3) and (4) to obtain
![]()
(5)
with ![]()
a constant produced by the renormalization scheme. ![]()
is useful for the determination of the free energy and therefore of all the thermodynamic quantities of system.
Replacing the expressions of the Equations (3) and (4) in Equation (5), and knowing that ![]()
and![]()
, we obtain the following equation
![]()
(6)
Since ![]()
and![]()
, the previous relation can take twelve forms. But taking into account the fact that cases ![]()
and ![]()
are equivalent, we obtain six different forms ![]()
that we report below:
For ![]()
![]()
(7)
For ![]()
![]()
(8)
For ![]()
![]()
(9)
For ![]()
![]()
(10)
For ![]()
![]()
(11)
For ![]()
![]()
(12)
The Equations (7) to (12) and the bond-shifting process yield the final renormalized couplings ![]()
and![]()
. Thus, we obtain the Migdal-Kadanoff renormalized interactions:
![]()
(13)
Numerical analysis of these equations gives the flow in the parameter space of the Hamiltonian. We have already obtained [48] phase diagrams of the infinite Blume-Capel model (2D and 3D) and the table of fixed points that govern the phases and phase transitions. In the reference [48] , the second-order phase transitions are described by the fixed point C, the first order by the fixed point A and the tricritical point by the fixed point T. The various phase diagrams of the infinite model were also obtained according to the ratios of the interactions of the model.
Our results in the infinite model can be compared with those obtained by other methods: concerning the existence of tricritical point and its domain according to the values of the ratios of the interactions, we are in agreement with mean field theory result [52] , cluster variational theory [53] and Monte Carlo study [54] . At low temperatures, those approaches predict the possibility of first order transition between two ordered phases terminating at an end point. In our Migdal-Kadanoff approximation, we find only first order transition between ordered and disordered phases. Another common point is that there is no universality violation in the phase diagrams obtained. There is no marginality in all the fixed points obtained by Migdal-Kadanoff approach. Note that in general theory, the universality in phase transitions and critical phenomena is expressed explicitly by the existence of the non marginal fixed point describing a line or surface phase transitions. Each line or surface is consequently described by the same critical exponent evaluated at the fixed point by linearizing the renormalization group transformation.
Another comparison is possible, with the pure BC model S = 1 or S = 3/2. In this case all those approximations are in agreement with the existence of the tricritical point in the integer spin case, but for the half integer spin, there exist a first order transition between two ordered phases at low temperature and the non existence of disorder in this domain. In reference [53] , we are agreeing with the fact that the phase diagrams obtained in the mixed BC model are reminiscent of that in pure model.
2.2. Semi-Infinite Blume-Capel Model
We consider a system consisting of two mixed spin-1 and spin-3/2 sublattices, limited by a surface where the single-ion anisotropies acting on the spin-1 and spin-3/2 are denoted, respectively, ![]()
and![]()
.
In the bulk, we keep the same notations of Section 2.1. On the surface, the reduced bilinear exchange interaction J, the reduced biquadratic interaction K and the interaction C mentioned in the Hamiltonian (2), are denoted by![]()
, ![]()
and![]()
. Therefore, our system is described by the following reduced Hamiltonian:
![]()
(14)
Each spin at the surface can interact with a spin located in the bulk and increasingly with its first neighbors at the surface. With this new environment, some new critical properties will appear at the surface which will have recursion equations coupled to the bulk. This latter keeps the same equations as in the infinite model, forming an invariant subspace.
Concerning the surface, we can write the recursion equations in the following compact form [55] [56] :
![]()
(15)
with![]()
. The functions![]()
, obtained by decimation, are those defined for the infinite
model![]()
, b is the space scale factor and d is the geometric dimension.
We introduce the ratios![]()
, ![]()
and ![]()
linking the bulk and surface interactions. The
phase diagrams are constructed in the plane ![]()
according to the values taken by ![]()
and in the plane ![]()
according to the values taken by![]()
.
In the renormalization procedure, the critical behaviors are derived from fixed points, by evaluating the eingenvalues of the transformation as![]()
. But this is only the asymptotic critical behavior, and there are some corrections due to the nonlinear scaling fields. In reference [51] , for precision Monte Carlo studies of the critical behavior of the 3d Ising model, the author gives the value of the anisotropy of the BC model, for which the amplitude of leading corrections to scaling vanishes.
In our case, the additive terms of the infinite and semi infinite (bulk terms) model can be considered useful for finding a point of the second order transition line for which the irrelevant field vanishes.
3. Results and Discussions
The calculation of the critical temperature of infinite Blume-Capel model with mixed spins SA = 1 and SB = 3 /2 (Section 2.1), in the three-dimensional case d = 3, shows three main types of diagram, labelled I, II and III. These types of diagrams can be classified as follows:
Type I: appears in the diagrams ![]()
for: ![]()
(Figure 3 is an example of this type).
Type II: appears in the diagrams ![]()
for: ![]()
(Figure 4 is an example of this type).
Type III: appears in the diagrams ![]()
and ![]()
for: ![]()
(Figure 5 is an example of this type).
The phase diagrams in the ![]()
plane for ![]()
and for the three-dimensional system are shown in Figure 3. ![]()
denotes the tricritical temperature for d = 3. This type of diagram is characterized by the transitions of first- and second-order which are separated by the tricritical point.
The second and third types of phase diagrams (Figure 4 and Figure 5) are characterized by the presence of only second-order transitions and they have different shapes.
Using renormalization-group calculations in the semi-infinite case (Section 2.2), we have obtained five generic types of phase diagram, illustrated in the ![]()
plane for several values of ![]()
and![]()
, reported in Figures 6(a)-(e). They show a variety of ordinary, extraordinary and special phase transitions. To classify the different types of phase diagram, we shall proceed as follows:
1) For ![]()
and![]()
, the surface and the bulk order at the same temperature. The system exhibits only an ordinary phase transition of second order. Figure 6(a) represents a typical phase diagram.
![]()
Figure 4. (Diagram of type II): The transition temperature of the mixed spin-1 and spin-3/2 Ising system as a function of ![]()
for the parameter ![]()
= 10 and d = 3 (Reference [48] ).
![]()
Figure 5. (Diagram of type III): The transition temperature of the mixed spin-1 and spin-3/2 Ising system as a function of ![]()
for the parameter ![]()
= 0 and d = 3 (Reference [48] ).
2) For ![]()
and![]()
, we have indicated in Figure 6(b) a typical phase diagram among three qualitative types which have been determined. We have shown ordinary, extraordinary and surface phase transitions of second order. For a particular value of ![]()
there exist a special point S characterizing the phase transition.
3) For ![]()
and![]()
, the surface and the bulk order at the same temperature.
![]()
Figure 6. Typical phase diagrams in the plane ![]()
for the three-dimensional semi-infinite BC model with mixed spins (SA = 1 and SB = 3/2). ![]()
represent a special point, an ordinary tricritical point and a special tricritical point, respectively. The symbols SD, BD, SO and BO denote, respectively, surface disorder, bulk disorder, surface order and bulk order phases.
This ordinary phase transition can be first-order, second-order or tricritical. Figure 6(c) represents a typical phase diagram.
4) For ![]()
and![]()
, we can observe ordinary first-order, ordinary second- order, extraordinary second-order and surface second-order phase transitions. For two particular values of![]()
, we can also observe an ordinary tricritical point and a multicritical point. A typical phase diagram showing the various phase transitions is represented in Figure 6(d).
5) For ![]()
and![]()
, we can observe ordinary first-order, extraordinary second-order and surface second-order phase transitions. For a particular value of![]()
, we can also observe a special tricritical point![]()
. Figure 6(e) represents a typical phase diagram.
Thereafter, we present the phase diagrams in the ![]()
plane. In addition to the five phase diagrams found in the plane![]()
, we have obtained four generic types of phase diagrams. Figure 7 shows the dependence of the critical temperature ![]()
on ![]()
for different values of the parameters ![]()
and![]()
. We show a variety of phase transitions associated with the surface, including certain types of ordinary, extraordinary and special phase transitions. To classify the different types of phase diagrams, we shall proceed as follows:
a) For ![]()
and![]()
, the system exhibits only an ordinary phase transition of second order. Figure 7(a) represents a typical phase diagram.
b) For ![]()
and![]()
, the corresponding phase diagram is characterized by extraordinary and surface second-order phase transitions. A typical phase diagram showing the various phase transitions is represented in Figure 7(b).
c) For ![]()
and![]()
, we have indicated in Figure 7(c) a typical phase diagram among three qualitative types which have been determined. We have shown ordinary, extraordinary and surface phase transitions of second-order. For two particular values of ![]()
there exist two special points (![]()
and![]()
) characterizing the special phase transition, where a second-order transition line meets two second-order transition lines, particularly lines of extraordinary and surface transitions. At these special points the surface and the bulk of the system become ordered simultaneously.
d) For ![]()
and![]()
, we obtain three main qualitative types of phase diagrams; one of them is reported in Figure 7(d). It shows ordinary, extraordinary and surface phase transitions of second-order. The three transition lines meet at two special phase transition points (![]()
and![]()
).
Let us comment the types of phase diagrams obtained by Migdal-Kadanoff renormalization:
1) The presence of a semi infinite surface gives rise to a variety of new phase diagrams. Are highlighted, ordinary transitions (e.g. Figure 6(a)), extraordinary transitions (Figure 6(b)), surface transitions (Figure 7(b)) and special transitions (Figure 7(d)).
2) Each of these phase transitions is represented by a different fixed point, and that they belongs to a new universality class different from that of the bulk. For example, the surface performs two different types of second order phase transitions. The first has a temperature higher than that of the bulk; this surface transition is described by the fixed point (OB, CS), where OB is the fixed point (disorder) of the bulk [48] , and CS is that of the surface: CS (JS = 1.55, KS = 0, ΔA(S) = ¥. ΔB(S) = −¥, CS = −0.47). The second possible transition occurs at the same temperature as that of the bulk; it is the special transition, represented by another different fixed point (CB, CSp). CB is the second order fixed point of the bulk [48] , and CSp the surface one with coordinates CSp (JS = 1.29, KS = 0, ΔA(S) = ¥, ΔB(S) = −¥, CS = −0.074).
Lipowski had already mentioned the expected difference between the two approaches (MF and RG), in the study of semi infinite Potts model [60] . In fact the mean field treats the bulk as field acting on the surface and the surface order parameter can cause a non ordinary first order phase transition. In the Migdal-Kadanoff renormalization procedure, the fixed point surface obeys the bond-moving relation (15). When the bulk fixed point is at a finite temperature, the surface may converge to a finite fixed point and have a surface transition. While, if the bulk fixed point is at T = 0 K (JB infinite), the surface one is also at 0 K. In particular, the fixed point of the bulk first order phase transition is precisely at 0 K, which causes ordinary first order transitions at surface.
The experimental results confirm the existence of a continuous transition at surface, while the bulk exhibit simultaneously a first order transition, what is called in the literature “surface induced disordering” (SID). This type of transition was highlighted in the Cu3Au alloy, see reference [61] . It has been observed that when the bulk exhibits a first order transition, the order parameter of the surface vanishes continuously and in reference [62] , a theoretical study has been made using landau free energy. For a complete comparison, it is interesting to treat this model by the mean field approximation and to compare the types of phase diagrams with those obtained by renormalization.
4. Conclusions
During this work, we have studied the pure Blume-Capel model in the semi-infinite case. To achieve our goal, we have determined the global phase diagrams of the mixed spin-1 and spin-3/2 in the semi-infinite system with different single-ion anisotropies acting on the spin-1 and spin-3/2 (on the surface and in the bulk) by using the Migdal-Kadanoff renormalization group technique, which combines decimation (with a space scale ration b = 3) and bond shifting. In the phase diagrams, the critical temperature lines versus single-ion anisotropies are shown. We have classified the various phase diagrams at fixed ![]()
and![]()
, finding new types of phase diagrams featuring a variety of phase transitions and multicritical points .
A comparison with the types of phase diagrams in the pure semi-infinite model with S = 1 and S = 3/2 obtained by the renormalization and the mean field approaches was performed.
In perspective, we hope that this work could stimulate further theoretical and experimental works on ferrimagnetic systems such as mixed spins with random fields in finite, infinite and semi-infinite systems.
NOTES
![]()
*Corresponding author.