Application of Snow Melt Runoff Model in a Mountainous Basin of Iran ()
Received 11 December 2015; accepted 21 February 2016; published 24 February 2016

1. Introduction
Monitoring snow distribution in mountainous basins and understanding snow processes are imperative to accurate stream flow simulation which is of great significance to optimal water resources management and planning. Basin-scale snowfall estimation has faced difficulties due to highly spatial and temporal variability of snow cover information and data scarcity in mountainous areas; however the progress of satellite remote sensing makes it possible to provide the most accurate snow cover information which can be applied for snowmelt runoff modeling, creating more reliable results in terms of river flow simulation and forecast. These products provide the most significant parameter for the Snowmelt Runoff Model (SRM) which was developed by Martinecin 1975 for small European basins and has been most widely used both in simulation and forecast [1] . The model also successfully underwent tests by the World Meteorological Organization (WMO) with regard to runoff simulation [2] . To date the model has been applied by various agencies, institutes and universities in over 100 basins, situated in 29 different countries. Runoff computations by SRM appear to be relatively easily understood and more than 80% of applications of SRM have been performed by independent users [3] . The obtained results of modeling suggest that the SRM can simulate with success in both diurnal water discharge and snow water equivalent in the mountainous study area [4] . The input variables of model are the meteorological data and the snow cover area. Since quality of input data is directly related to the model accuracy and efficiency, the calculation and determination of variables and parameters are most important to the model simulation. Hence, according to the previous studies, the SRM research worldwide has been mainly concentrated on the acquisition of variables, optimization of parameters, and proper analyses of the hydrological and physical characteristics of a basin [5] . Since the various applications of SRM mainly differ in the selection of data sources, determination and calculation of parameters, this study has aimed at examining the adaptability of the model structure based on the availability of the variable and estimation of parameters for a semi-arid mountainous basin in East North of Iran.
2. Methodology
2.1. Study Area
The model was applied to Samalghan Basin located in the East North region of Iran where the boundaries can be given by longitudes from 37˚24'39" to 37˚29'07" east and latitudes 56˚59'60" to 56˚37'46" north. It is a sub basin of Atrak River which flows into the Caspian Sea. The basin boundary was defined by the location of the hydrometric station installed in the lowest point of the catchment (Figure 1). The drainage basin area is 1147 km2 and the length of the Samalghan River is 58 km. Elevation zones were delineated in intervals of about 500 m, after analyzing the elevation range between the hydrometric station and the highest point in the basin. The zones were defined in order to apply the various model variables and parameters to each zone for the accuracy of the runoff calculation. The flat part of the basin has heights of up to 700 m and makes up 35% of the entire basin area. Foothills with highlands, with heights from 750 to 2675 m, make up the remaining 65% and this is where the majority of the runoff originates. The elevation range of the basin and the Area-Elevation curve are shown in Table 1 and Figure 2.
2.2. Description of Model
Snowmelt Runoff Model (SRM) is designed to simulate and forecast daily stream flow in mountainous basins where snowmelt is a major runoff factor. The model uses snow cover information and meteorological data as
![]()
Figure 1. Location of study area in the North East of Iran.
![]()
Table 1. Catchment areas under different elevation zones.
![]()
Figure 2. Area-elevation curve extracted from DEM analysis.
input variable. Each day, the water produced from snowmelt and from rainfall is computed, superimposed on the calculated recession flow and transformed into daily discharge from the basin according to Equation (1) [3]
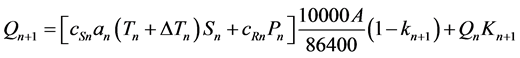 (1)
(1)
where:
Q = the average daily discharge (m3∙s−1);
c = the runoff coefficient expressing the losses as a ratio of runoff to precipitation, with 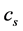 referring to snowmelt and
referring to snowmelt and 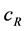 to rain;
to rain;
a = the degree-day factor (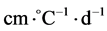 ), which indicates the snowmelt depth resulting from one degree-day;
), which indicates the snowmelt depth resulting from one degree-day;
T = the number of degree-days (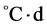 );
);
∆T = the adjustment by temperature lapse rate when extrapolating the temperature from the station to the average elevation of the basin or zone (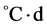 );
);
S = the ratio of the snow cover area (SCA) to the total area;
P = the precipitation contributing to runoff (cm), which is determined by the preselected threshold temperature CRIT T: if precipitation is determined to be new snow, it is kept in storage over the hitherto snow-free area until melting conditions occur;
A = the area of the basin or zone (km2);
k = the recession coefficient indicating the decline of discharge in a period without snowmelt or rainfall:
 (m and m + 1 are the sequence of days during a true recession flow period);
(m and m + 1 are the sequence of days during a true recession flow period);
n = the sequence of days during the discharge computation period.
Model calculates the daily average stream flow on the (n + 1) day by the addition of snowmelt and precipitation contributing to runoff and discharge on the preceding day. Generally, a seasonal or yearly runoff volume can be estimated with a known discharge in a watershed, as long as the model input variables are provided and parameters are determined. SRM can be used to simulate the daily stream flow of a snowmelt season, in a year, or in a sequence of years, to provide short-term and seasonal runoff forecasts, and to evaluate the potential effect of climate change on the seasonal snow cover and runoff [3] [6] .
2.3. Inputs Variables and Parameters
There are three main input variables and eight parameters are needed for the simulation process. Variables include air temperature, precipitation and the snow cover area (SCS) applying during the snowmelt period and runoff is calculated by converting the degree-days above the critical temperature into melt depths by the degree-day factor. SRM parameters, including the temperature lapse rate, runoff coefficient, degree-day factor, recession coefficient, critical temperature, rainfall-contributing area and lag time, are also of vital importance to the model performance. In addition to these, the area-elevation curve of the basin is also required. Model parameters can be well estimated and optimized if the given basin or climate characteristics, such as soil conditions, vegetation cover, antecedent precipitation, and runoff data, are available [3] . It is also interesting to note that the most significant stage to set up the model is the choice of remote sensing data which is accessible and appropriate enough for analysis and extraction of snow cover map in the particular study area. Since SCA is an imperative input of model in a snow dominated basin, errors in determining it are directly proportional to the resulting errors in the calculated snowmelt and unreliable output of model [7] . However, there is no in situ measurement over the snow season and it is impossible to compare the accuracy of MODIS snow maps with the actual snow cover in the study area. The main reasons to have disagreement between MODIS and in situ data are the high cloud cover frequency in the area and the current version of the MODIS cloud-mask that appears to frequently map edges of snow-covered areas and land surfaces [8] . In order to minimize the cloud cover and maximize the snow cover, MODIS-8 daily snow cover products are used in deriving the snow depletion curve for simulation of snowmelt runoff in basins of Turkey [5] [8] . In this study, the Moderate Resolution Imaging Spectroradiometer MODIS composite 8-day maximum snow-cover extent data were selected to create a snow cover database. The database includes 46 processed satellite images, completely covering the Samalghan basin from 2010-2011. The MODIS snow-mapping algorithm is fully automated and is based on the normalized difference snow index (NDSI) and a set of thresholds [9] . Based on NDSI and threshold values, snow cover pixels are separated from non-snowy areas using Equation (2):
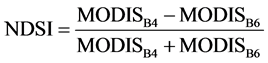 (2)
(2)
The calculation of maximum SCA was implemented by analysis of the prepared database using NDSI in ERDAS IMAGINE over the period of snow accumulation and ablation of 2010-2011. The images were re-pro- jected to World Geodetic System 1984 (WGS84), Universal Transverse Mercator (UTM) Zone 40 with a cell size of 500 m. Using these satellite data, the snow line is delineated by visual interpretation and the percentage of snow cover area in each elevation zone is calculated and applied to the model. A snow cover extracted as mentioned is shown in Figure 3.
Since snow accumulation and ablation is influenced by energy balance in the process of transforming to runoff, temperature can be considered, in fact, as the significant melting parameter. Temperature data are measured by meteorological stations at a certain elevation in which the gages are installed. Since temperature varies with elevation, therefore, temperature elevation relationship helps to estimate the temperature at the unmeasured locations [10] . Previous studies have utilized different methods to estimate climatic factors. Dey et al. presented the application of SRM in the Western Himalayas. They used ambient air temperature values from one climate station outside of the basin and degree-day values determined by extrapolating the ambient air temperature to the mean elevation according to certain temperature lapse rates [11] . At the current study, temperature data recorded from five different stations at different elevation levels were applied to obtain zonal temperature by extrapolating the station altitude to mean zone altitude with a certain temperature lapse rate. The relation between elevation and daily average temperature was developed for different stations as given in Figure 4. Temperature laps rate estimated is 5.1˚C/km.
The evaluation of representative areal precipitation is also challenging in mountainous basins. Particularly in basins with a great elevation range, the precipitation input may be underestimated if only low altitude precipitation stations are available. It is recommended to extrapolate precipitation data to the mean hypsometric altitudes of the respective zones by an altitude gradient [3] . In order to provide precipitation input data for the study area, eleven rain gauges in different elevations are selected. Four of these installed stations are inside the catchment and the others are outside of it. As the measurement of rainfall or snowfall results in a point data, spatial precipitation data are obtained by creation of Thiessen polygon. Each Thiessen polygon defines an area of influence around its station point so that weighted rainfall in each elevation zone is calculated by application of the Thiessen polygon and the elevation zones. These steps are implemented by ArcGIS. In terms of measured runoff data, there is a hydrometric station in the catchment’s outlet. Daily stream flow recorded in this station is applied to
![]()
Figure 3. Snow cover derived through process of MODIS terra on data for 20.03.2011.
![]()
Figure 4. Relation between average daily temperature and elevation.
validate the results of model.
3. Estimation of Model Parameters
Successful application of the SRM depends on how accurate the model parameters are estimated. However, in the studied basin circumstance where the ground measurement of snow is scarce there is no opportunity to calibrate the model parameters by historical data. It is tried, therefore, to estimate the required parameters based on the existing series of hydro-meteorological data, the empirical regression equations, assumption or using the default values given in the model. The model was tested in several predetermined steps and obtained accurate assumed parameters at a preliminary stage.
3.1. Runoff Coefficient, C
This factor simply indicates the percentage of rainfall/snowfall converted to runoff. On a long term basis, it should correspond to the ratio of the measured precipitation to the measured runoff. In fact, comparison of historical precipitation and runoff ratios provide a starting point for the runoff coefficient values [3] . Regarding to the availability of runoff and precipitation data in the outlet of the study basin, daily runoff coefficient was estimated based on the data series recorded in the meteor-hydrological stations.
3.2. Critical Temperature, CRITT
The critical temperature determines whether the measured or forecasted precipitation is rain or snow. SRM needs the critical temperature only in order to decide whether precipitation immediately contributes to runoff (rain), or, if T < CRITT, whether snowfall took place. In this case, SRM automatically keeps the newly fallen snow in storage until it is melted on subsequent warm days [3] . Critical temperature is assumed as 0˚C in this study to determine whether precipitation is rain or snow in each elevation zone.
3.3. Recession Coefficient, k
The recession coefficient is an important feature of SRM since (1 − k) is the proportion of the daily meltwater production which immediately appears in the runoff. Analysis of historical discharge data is usually a good way to determine k [3] . Observed values of Qn and Qn+1 recorded by hydrometric station are compared on log-log scale and the k-value is determined on a daily basis, which is the slope of the best-fit line.
3.4. Time Lag, L
The characteristic daily fluctuations of snowmelt runoff enable the time lag to be determined directly from the hydrographs of the past years. The lag time for the Samalghan basin estimated as 12 hours based on the previous physiographic studies of the area conducted by Water Regional Authority [12] . Using the estimated hydrological and meteorological parameters and the snow cover derived from digital image processing of MODIS data, the daily stream flow can be calculated by SRM.
4. Discussion
As discussed earlier, the 12-month hydro-meteorological data was provided to simulate the stream runoff for Samalghan basin over a period of October 2010 to September 2011. Since there is no automated station in the experimental basin which makes it possible to record and collect in situ depth and density of snow, it is impossible to validate the process of estimation of snow cover based on the MODIS snow products. Thus, the observation of daily stream flow recorded by the hydrometric station in the outlet of the study catchment was the main measured data to validate the result. A visual inspection, at first glance, shows that the simulated values are almost totally in conformity with the measured stream flow data. The comparison between the measured and calculated hydrographs is shown in Figure 5. The statistical criterions for evaluation of the model application efficiency are the coefficient of determination ( ) and the volume difference (
) and the volume difference (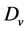 ) for a more objective assessment of how well the simulation has been carried out. The coefficient of determination is computed as follows [13] .
) for a more objective assessment of how well the simulation has been carried out. The coefficient of determination is computed as follows [13] .
![]() (3)
(3)
![]() is the measured daily discharge;
is the measured daily discharge;
![]() is the computed daily discharge;
is the computed daily discharge;
![]() is the average measured discharge of the given year or snowmelt season;
is the average measured discharge of the given year or snowmelt season;
n is the number of daily discharge values.
The deviation of the runoff volumes ![]() is computed as follows:
is computed as follows:
![]() (4)
(4)
![]() is the measured yearly or seasonal runoff volume;
is the measured yearly or seasonal runoff volume;
![]() is the computed yearly or seasonal runoff volume.
is the computed yearly or seasonal runoff volume.
![]()
Figure 5. Measured and simulated hydrographs for the Samalghan river basin over the period of 2010-2011.
![]()
Table 2. Results of SRM simulation for the Samalghan basin.
Based on the result of SRM application in the study area, the coefficient of determination ![]() was 0.82 which showed a relatively good correlation between the observed daily runoff and simulated ones. The average deviation of computed runoff with measured runoff was −4.7%. The statistical test (Table 2) depicted the relatively satisfactory results of the performance of SRM in the study basin. However, in order to obtain more accurate simulating results, the model parameters should be optimized based on the basin hydrological conditions.
was 0.82 which showed a relatively good correlation between the observed daily runoff and simulated ones. The average deviation of computed runoff with measured runoff was −4.7%. The statistical test (Table 2) depicted the relatively satisfactory results of the performance of SRM in the study basin. However, in order to obtain more accurate simulating results, the model parameters should be optimized based on the basin hydrological conditions.
5. Conclusion
Obviously, accurate simulation and forecast of snowmelt runoff have been the key factors to plan and develop in semi-arid catchments where mountain-fed rivers are of great importance to provide secure water resources. Thus the practicality of SRM, particularly in a snow-dominated mountainous basin in a semi-arid climate condition was examined in this paper. Applying the snow cover mapping extracted from the MODIS products as the most important variable which plays a significant role in calculation of snow melt runoff by model facilitates the process of accurate simulation. The result of modeling in Samlaghan Basin illustrates that the model’s accuracy can be relatively acceptable, though most catchments in North East of Iran usually lack hydro-meteorological measurements spatially in terms of snow field measurements that face modeling with difficulty and even make it impossible. However, there is no way to optimize the modeling process unless the most accurate snow cover remote sensing data and innovative ways of model parameterization are employed.
Acknowledgements
The authors gratefully acknowledge the North Khorasan Water Regional Company to provide data which have been used in this study.