The 4-Acyclic Edge Coloring of Graphs with Large Girths

Yuwen Wu^1*, Yan Xia²

¹School of Information, Beijing Wuzi University, Beijing, China.
²Institute of Policy and Management, Chinese Academy of Sciences, Beijing, China.

DOI: 10.4236/jamp.2015.312183                

Abstract

A proper edge coloring of a graph is acyclic, if every cycle of the graph has at least 3 colors. Let r be a positive integer. An edge coloring is r-acyclic if it is proper and every cycle C has at least  colors. The r-acyclic edge chromatic   number of a graph G is the minimum number of colors needed for any r-acyclic edge coloring of G. When r=4, the result of this paper is that the 4-acyclic chromatic number of a graph with maximum degree Δ and girth  is less than 18Δ. Furthermore, if the girth of graph G is at least , then .

Keywords

Girth, Edge Coloring, Acyclic Edge Coloring, Lovászlocal Lemma

Received 18 October 2015; accepted 13 December 2015; published 16 December 2015

1. Introduction

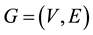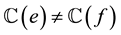All graphs considered in this paper are finite and simple. A proper edge coloring of a graph is a map such that for each pair of adjacent edges, where C denotes the color set. A proper edge coloring of G is called acyclic if there are no bichromatic (two-colored) cycles in G. In other words, the subgraph induced by the union of any two color classes is a forest. The acyclic edge chromatic number (also called the acyclicchromatic index) of a graph G, denoted by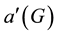, is the minimum number of colors required for any acyclic edge coloring of G. In 2001, Alon, Sudakov and Zaks [1] gave the well- known Acyclic Edge Coloring Conjecture.

Conjecture 1 (AECC). For every graph G with maximum degree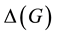, we have.

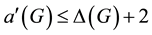Given a positive integer r, the r-acyclic edge coloring is a generalization of the acyclic edge coloring of graphs.

An edge coloring is r-acyclic if it is proper and every cycle C has at least 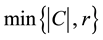colors. The r-acyclic edge

chromatic number 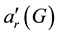of a graph G is the minimum number of colors needed for any r-acyclic edge coloring of G. This definition was first introduced by Gerke, Greenhill and Wormald [2] in 2006.

Gerke et al. [3] proved that for any graph G with girth. In [4] , we reduced the r-acyclic edge chromatic number of a graph G to when the girth of G

equals to.

In this paper we considered the r-acyclic edge coloring problems with r = 4. Using probabilistic arguments, we get some new upper bounds for the 4-acyclic edge chromatic number of arbitrary graph G.

Theorem 1. Let G be a graph with maximum degree and girth g.

1) If, then.

2) If, then.

2. Proof of Theorem 1

We make use of the Lovász Local Lemma as an important tool in our proof. Before giving the proof of Theorem 1, we state the general version of the Lovász Local Lemma (see [5] [6] for details) as follows.

Lemma 2. Let be events in an arbitrary probability space. Let the graph on the nodes be a dependency graph for the events; that is, assume that for each i, is independent

of the family of events. If there are reals such that for all i

then

so that with positive probability no event occurs.

Proof of Theorem 1.

When, can be proved easily. Hence we assume that Gisa graph with in our following arguments.

In the first step, we have to prove that there is an edge coloring, where c > 1 is a constant to be fixed later, such that satisfies the following four properties.

1) Every vertex has at most two incident edges of any single color;

2) There are no cycles colored by a single color;

3) There are no cycles colored by just two colors;

4) If the cycle D is colored by just three colors, there are such that they are adjacent and have the same color.

For each edge, we do the following random experiment. Choose a color uniformly and independently at random from the color set, and let it be the color of the edge e. In order to make sure the resulting random coloring satisfying properties (i)-(iv), we define four types of “bad events” as follows.

Type I. For each set of three edges incident with a given vertex, let be the event that all the three edges receive the same color.

Type II. Given a cycle D of length k, let be the event that all the edges of D are colored by the same color.

Type III. Given a cycle D of length l, let be the event that the edges of D are colored by just two colors.

Type IV. Given a cycle D of length h, let be the event that the edges of D are properly colored by three colors.

Obviously, if all the events of Type I, II, III and IV do not occur, then the edge coloring satisfies properties (i)-(iv).

Let us construct a graph H needed in Lemma 2. Denote X to be a set of three edges or a cycle D in the graph G, where all the three edges are incident with a given vertex and colored by the same color, and all the edges of are colored by a single color, or colored by two colors, or properly colored by three colors. Let =

{| is an event of type I, II, III or IV}. For each pair of nodes, and are adjacent if and only if. Since the occurrence of each event depends only on the colors of the edges in X, H is a dependency graph for our events. Furthermore, a node of H is called a node of type i if it corresponds to an event of type i, where. In order to apply the Local Lemma, we have to estimate the probability of every event and the number of nodes of each type in graph H which are adjacent to a given node.

Lemma 3. Let be the edge set of type I and D be a cycle in the graph G.

1) For each event of type I,;

2) For each event of type II,;

3) For each event of type III,;

4) For each event of type IV,.

Let e be any given edge of graph. The number of sets which consist of e and two other edges adjacent to e at the same vertex, is less than. For every, no edge lies in more than cycles of length k. For every node, let x be the number of edges contained in X. Lemma 3 tells us that the number of nodes of type I, II, III and IV adjacent to in graph H is no more than, , and, respectively.

Let, , and be the values corresponding to events

of type I, II, III and IV, respectively, where are constants to be determined later. Applying the Local Lemma, we have that, with positive probability none of bad events occur, provided the following four inequalities hold for every.

(1.1)

(1.2)

(1.3)

(1.4)

Let. It is well-known that is an increasing function which converges to 1/e as z tends

to be infinity. Define. So we have

and

Furthermore, since, we have. Thus, the following three inequali-

ties, and

can be proved to be true.

In order to prove inequalities (1.1)-(1.4) holds, we just need to show that the following four inequalities (1.5)-

(1.8) hold for every.

(1.5)

(1.6)

(1.7)

(1.8)

With the help of the MATLAB calculations, we receive the minimum values of c and corresponding values of and g. Therefore, there is a random edge coloring satisfying properties (i)-(iv) which needs colors.

When, and decrease with the increasing of l and h, respectively. Therefore,

when, we set. It can be verified that the inequalities (1.5)- (1.8) are satisfied by setting. When, we set. And it can be verified that the inequalities (1.5)-(1.8) are satisfied by setting.

From the above argument, we know that, there is an edge coloring of the graph G which satisfies properties (i)-(iv).

Now turn to the second step of our proof. For every color, let be the induced subgraph

of G by the edges with the color i. From properties (i) and (ii), we know that and consists of

some disjoint paths. Therefore, the edges of can be recolored by two new colors, which becomes a proper 2-edge coloring of.

After similar arguments of every color, we get a new proper edge coloring

of graph G. Furthermore, properties (iii) tells us there are no cycles colored by just two colors in the random edge coloring. If D is a cycle colored by three colors in, from property (iv), there are such that they are adjacent and have the same color. And then, will get two different colors in the new coloring, which makes the number of colors occurs in the cycle D is at least 4. If the random edge coloring makes the cycle D colored by at least 4 colors, then so does the new coloring. Hence, with the new coloring, there are at least 4 colors in every cycle of G.

In a word, is a 4-acyclic edge coloring of graph G with at most colors. And then, it is true that: when the girth, we have; and when, we have.

3. Remarks

This proof was finished mainly using the Lovász Local Lemma. We believe that with the use of more probabilistic methods, or more careful applications of the Local Lemma, the study of 4-acyclic edge colorings and r- acyclic edge colorings will go further.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Alon, N., Sudakov, B. and Zaks, A. (2011) Acyclic Edge Colorings of Graphs. Journal of Graph Theory, 37, 157-167.
[2]	Gerke, S., Greenhill, C. and Wormald, N. (2006) The Generalised Acyclic Edge Chromatic Number of Random Regular Graphs. Journal of Graph Theory, 52, 101-125.
[3]	Gerke, S. and Raemy, M. (2007) Generalised Acyclic Edge Colourings of Graphs with Large Girth. Discrete Mathematics, 307, 1668-1671.
[4]	Wu, Y.W. and Yan, G.Y. (2016) Improved Bounds on the Generalized Acyclic Chromatic Number. Acta Mathematicae Applicatae Sinica: English Series, to Appear.
[5]	Bondy, J. and Murty, U. (1976) Graph Theory with Applications. MacMillan, London.
[6]	Molloy, M. and Reed, B. (2002) Graph Colouring and the Probabilistic Method. Algorithms and Combinatorics. Springer, Berlin.