Pullback Exponential Attractors for Nonautonomous Reaction Diffusion Equations in H₀¹

Yongjun Li, Yanhong Zhang, Xiaona Wei

School of Mathematics, Lanzhou City University, Lanzhou, China.

DOI: 10.4236/jamp.2015.37087                

Abstract

Under the assumption that  g(t) is translation bounded in , and using the method developed in [3], we prove the existence of pullback exponential attractors in  for nonlinear reaction diffusion equation with polynomial growth nonlinearity( is arbitrary).

Keywords

Dynamical System, Pullback Exponential Attractors, Reaction Diffusion Equation

1. Introduction

Attractor’s theory is very important to describe the long time behavior of dissipative dynamical systems generated by evolution equations, and there are several kinds of attractors. In this article, we will study the existence of pullback exponential attractors (see [1]-[3]) for nonlinear reaction diffusion equation. This equation is written in the following form:

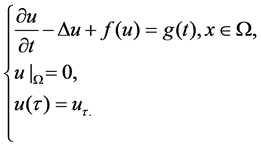(1.1)

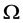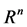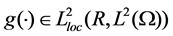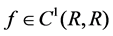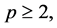
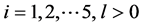
where is a bounded smooth domain in, , and there exist 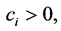such that

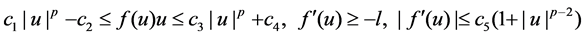(1.2)

for all.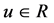

The Equation of (1.1) has been widely studied. For the autonomous case, i.e., 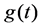does not depend on the time, the asymptotic behaviors of the solution have been studied extensively in the framework of global attractor, see [4]-[6]. For the nonautonomous case, the asymptotic behaviors of the solution have been studied in the framework of pullback attractor, see [7]-[9]. Recently, the theory of pullback exponential attractor have been developed, see [1]-[3], and some methods are given to prove the existence of pullback exponential attractors.

In order to obtain the existence of pullback exponential attractors of (1.1), we will need the following theorem.

Theorem 1.1. ([3]) Let 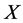be an uniformly convex Banach space, be the set of all bounded subsets of be a time continuous process in. Then the process exist pullback exponential attractors in if the following conditions hold true:

(1) There exists an uniformly bounded absorbing set, that is, for any and, there exists such that

(1.3)

(2) There exist, and a finite dimension subspace, such that

(1.4)

(1.5)

(1.6)

for all and, where is independent on the choice of, and is the norm in, is the identity operator, is a bounded projector, is the dimension of.

2. Some Estimates of Equation (1.1)

In this section, we will derive some priori estimates for the solutions of (1.1) that will be used to construct pullback exponential attractors for the problem (1.1).

For convenience, hereafter let be the norm of and an arbitrary constant, which may difference from line to line and even in the same line. We define with scalar product and norm

; let and denote the scalar product and norm of and for all, set is the first eigenvalue of.

For the initial value problem (1.1), we know from [4]-[6] that for any initial datum, there exists a unique solution for any.

Thanks to the existence theorem, the initial value problem is equivalent to a process define by

.

In addition, we assume that the function is translation bounded in, that is

(2.1)

By (2.1), for, we have

(2.2)

Lemma 2.1. ([7]-[9]) Assume that satisfy (1.2) and (2.2), be a weak solution of (1.1), then for any, we have the following inequality:

(2.3)

and

(2.4)

Lemma 2.2. Assume that satisfy (1.2) and (2.2), be a weak solution of (1.1), then the following inequality holds for

(2.5)

Obviously, for any bounded, there exist, such that

for any and. (2.6)

Proof. Let, then by (1.2), we get there exist, , such that

. (2.7)

Taking inner product of (1.1) with in and using (2.7), we get

. (2.8)

Multiply (1.1) by, we have

since, we obtain

.

Combining (2.7), we get

. (2.9)

Thanks to Poincaré inequality, we have

. (2.10)

Let, by (2.9) and (2.10), we obtain

,

which imply

,

integrating, we get

,

using (2.3) and (2.4), we get the inequality (2.5).

Lemma 2.3. Assume that satisfy (1.2) and (2.1), be a weak solution of (1.1), then the following inequality holds for

, (2.11)

Here for any.

By the assumption (2.1) and for, we get

. (2.12)

Proof. Multiply (1.1) with, we obtain

. (2.13)

By (1.2) and Young’s inequality, we have

,.

By (2.13), we get

integrating and using (2.4), we get

. (2.14)

Multiply (1.1) with, we obtain

.

By (2.1), we get

.

Using Young’s inequality

.

By the above inequality, we have

integrating and using (2.12) and (2.14), we get (2.11) holds.

Lemma 2.1, lemma 2.2 and lemma 2.3 show that the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set in, that is

Theorem 2.4. Assume that satisfy (1.2) and (2.1), be a weak solution of (1.1), then the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set , that is, for any bounded set, there exists, such that for any.

In fact, using the same proof as in Lemma 2.3, we can get the following result.

Lemma 2.5. Assume that satisfies (1.2), is translation bounded in, that is be a weak solution of (1.1), then the process generated by the equation (1.1) have

an uniformly pullback bounded absorbing set, that is, for any bounded set, there exists, such that for any.

3. Pullback Exponential Attractors

In this section, we will use Theorem 1.1 to prove that the process generated by Equation (1.1) exists a pullback exponential attractor.

First we assume that the function is normal ([10]) in, that is, for any, there exists such that

. (3.1)

Obviously, is normal in implying that is translation bounded in.

We set, since is a continuous compact operator in, by the classical spectral theorem, there exist a sequence, and a family of elements of

which are orthogonal in such that,. Let in and is a orthogonal projector. For any, we write

.

Theorem 2.4. Assume that satisfies (1.2), is translation bounded in and (3.1) holds, then the process generated by the equation (1.1) have a pullback exponential attractor.

Next, we will verify that the process generated by (1.1) satisfy all the conditions of Theorem 1.1.

Proof. By Theorem 2.4, there exists, such that for any. Let, we obtain is also an uniformly pullback bounded absorbing set in and for any.

We set, to be solutions associated with Equation (1.1) with initial data, since is the uniformly pullback bounded absorbing set in, so there exists such that, Let, by (1.1), we get

(3.2)

Taking inner product of (3.2) with in, we have

(3.3)

Taking into account (1.2) and Holder inequality, it is immediate to see that

,

and

By Lemma 2.5, we get

(3.4)

Using (3.3), we obtain, hence

. (3.5)

Let, be the project in. Taking inner product of (3.2) with in, we have

. (3.6)

.

Taking into (3.4) account, we obtain

,

Using the Poincaré inequality, we get, by Gronwall’s Lemma, we have. Using (3.5), we get

. (3.7)

Let, be the project in. Taking inner product of (1.1) with, we get

Since, , and by Poincaré inequality, we have

By Gronwall’s lemma, we get

.

By (3.1), we obtain that there exists, such that for any, and for any, there exists, such that, so we get

and, we have

(3.8)

Let, by (3.5), we get

(3.9)

Since, for, from (3.7) and (3.8), there exist, such that

(3.10)

(3.11)

By Theorem 2.4 and (3.9)-(3.11), we know that the process generated by (1.1) satisfy all the conditions of Theorem 1.1.

Funds

This work was supported by the National Nature Science Foundation of China (11261027) and Longyuan youth innovative talents support programs of 2014, and the innovation Funds of principal (LZCU-XZ2014-05).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Langa, J., Miranville, A. and Real, J. (2010) Pullback Exponential Attractors. Discrete and Continuous Dynamical Systems—Series A, 26, 1329-1357.
[2]	Czaja, R. and Efendiev, M. (2011) Pullback Exponential Attractors for Non-Autonomous Equations, Part I: Semilinear parabolic Problems. Journal of Mathematical Analysis and Applications, 381, 748-765. http://dx.doi.org/10.1016/j.jmaa.2011.03.053
[3]	Li, Y., Wang, S. and Zhao, T. (2015) The Existence of Pullback Exponential Attractors for Non-Autonomous Dynamical System and Application to Non-Autonomous Reaction Diffusion Equations. J. Appl. Anal. Comp (in press).
[4]	Chepyzhov, V. and Vishik, M. (2002) Attractors for Equations of Mathematics Physics. 49, American Mathematical Society Colloquium Publications, AMS.
[5]	Temam, R. (1997) Infinite-Dimensional Dynamical Systems in Mechanics and Physics. 68, Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0645-3
[6]	Ladyzhenskaya, O. (1991)Attractors for Semigroups and Evolution Equations. Cambridge University Press, Cambridge, UK. http://dx.doi.org/10.1017/CBO9780511569418
[7]	Song, H. and Wu, H. (2007) Pullback Attractor for Nonlinear Autonomous Reaction Diffusion Equations. Journal of Mathematical Analysis and Applications, 325, 1200-1215. http://dx.doi.org/10.1016/j.jmaa.2006.02.041
[8]	Song, H. (2010) Pullback Attractors of Nonautonomous Reaction Diffusion Equation in . Journal of Differential Equations, 249, 2357-2376. http://dx.doi.org/10.1016/j.jde.2010.07.034
[9]	Li, Y. and Zhong, C. (2007) Pullback Attractors for the Norm-to-Weak Continuous Process and Application to the Non-Autonomous Reaction Diffusion Equations. Appl. Math. Comp., 190, 1020-1029. http://dx.doi.org/10.1016/j.amc.2006.11.187
[10]	Lu, S., Wu, Q. and Zhong, C. (2005) Attractors for Nonautonomous 2D Navier-Stokes Equation with Normal External Forces. Discrete Cont. Dyna. Syst, 13, 701-719. http://dx.doi.org/10.3934/dcds.2005.13.701