Deriving of the Generalized Special Relativity (GSR) by Using Mirror Clock and Lorentz Transformations ()
1. Introduction
Einstein’s special relativity and general relativity represent one of the biggest achievements that change radically the space-time concept [1] . Special relativity (SR) succeeds in explaining the constancy of light speed in vacuum, long-time meson decay, and mass-energy conversion [2] .
SR shows that time, length, mass, and energy are velocity dependent [3] . Einstein extends his SR theory to the so-called general relativity theory (GR) which extends the space-time interval to the curved space GR succeeded in explaining a wide variety of astronomical phenomena. These include the Doppler red shift, which is interpreted as resulting from the universe expansion, the existence of relic microwave background, beside the gravitational red shift [4] .
These remarkable successes of SR and GR motivate some authors to promote SR within the frame of GR to produce the so-called Generalized Special Relativity (GSR) [5] .
Mubarak model, the matter energy-momentum tenser relation on the generalized Lorentz factor 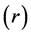 derived from the space-time interval in the curve space, was utilized to construct the seminal EGSR model; time, length, mass and energy are dependent on the field potential as well as velocity [6] .
derived from the space-time interval in the curve space, was utilized to construct the seminal EGSR model; time, length, mass and energy are dependent on the field potential as well as velocity [6] .
In this work two mirrors of certain length, acting as time clock, are under the action of gravity. The motion of the two mirrors under gravity is utilized to find a useful expression of time in the presence of the gravitational field. The speed of light is assumed to be constant in the gravity field. This assumption is confirmed by obtaining the light speed in accursed space time [7] .
This paper, which is concerned with the derivation of time dilation in the gravitational field, consists of 3 sections; apart from introduction, Section 2 is devoted for presenting EGSR theory. The derivation of time dilation in the gravitational field for any field is done in Section 3. The speed of light in the gravitational field is found in Section 4. Sections 5 and 6 are devoted for discussion and conclusion (Generalized Special Relativity [8] ).
According to GSR the expressions of time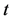 , length
, length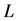 , and mass
, and mass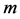 , are dependent on the velocity as well as field potential per unit mass and according to the relations.
, are dependent on the velocity as well as field potential per unit mass and according to the relations.
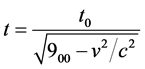 (1)
(1)
 (2)
(2)
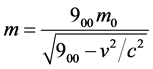 (3)
(3)
where
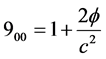 (4)
(4)
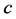 stands for light speed in vacuum, while
stands for light speed in vacuum, while 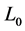 and
and 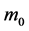 represent the rest time, length and mass respectively.
represent the rest time, length and mass respectively.
2. Time Dilation and Length Contraction
The expression of time in the presence of gravitational field can be found by considering two as a clock, with time intervals to representing the travel between the two mirrors as shown in Figure 1.
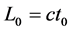 (5)
(5)
It moves with velocity up ward under gravity of acceleration g, the velocity of the lower mirror is given by
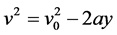 (6)
(6)
where 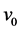 stands for the initial velocity, while
stands for the initial velocity, while 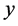 represents the displacement.
represents the displacement.
The vertical displacement ![]() is given by
is given by
![]()
The speed ![]() is also given by
is also given by![]()
Thus
![]() (7)
(7)
where:![]() →(8) is the average speed; a is any arbitrary acceleration in general. For the force
→(8) is the average speed; a is any arbitrary acceleration in general. For the force ![]() the potential
the potential ![]() is given by
is given by
![]()
where ![]() is the potential per unit mass and is given to be
is the potential per unit mass and is given to be
![]() (9)
(9)
Inserting (9) in (6) yields as shown in Figure 2.
![]() (10)
(10)
Since the point ![]() at which the photon hits the mirror is displaced
at which the photon hits the mirror is displaced ![]() meter vertically down ward, it follows that the light photon hits
meter vertically down ward, it follows that the light photon hits ![]() as shown in Figure 3.
as shown in Figure 3.
![]()
Figure 3. The mirror displaced ![]() meter vertically down ward.
meter vertically down ward.
Speed ![]() in the gravitational field the distance travelled by light is given indicates that
in the gravitational field the distance travelled by light is given indicates that
![]()
In view of Equations (7)-(10), one gets
![]()
![]()
![]() (11)
(11)
Thus:
![]() (12)
(12)
Using relation (10)
![]() (13)
(13)
If one consider ![]() and
and ![]() as standing for effective speed which is related to the maximum speed through the relations
as standing for effective speed which is related to the maximum speed through the relations
![]() (14)
(14)
Then relation (10) becomes
![]() (15)
(15)
And relation (13) becomes
![]()
For weak field
![]()
Thus
![]() (16)
(16)
Which coincides completed with the expression of time in the presence of the gravitational field obtain within the framework of GSR. Relation (14) it is important to note that of the factor ![]() in Einstein SR energy expression where
in Einstein SR energy expression where
![]() (17)
(17)
According to Equations (9) and (10) this relation holds for any field other than the gravitational field.
The length contraction can be obtained by considering a clock falling by sliding on a rod of a height![]() . For the observer moving with a clock the average speed is given by
. For the observer moving with a clock the average speed is given by
![]() (18)
(18)
where the rod is moving and accelerated w.r.t him, thus his length is![]() . But for an observer at rest w.r.t the rod, the rod length is
. But for an observer at rest w.r.t the rod, the rod length is ![]() for him and the clock time is it. Thus the speed
for him and the clock time is it. Thus the speed ![]() is given by
is given by
![]() (19)
(19)
Thus, with the aid of Equations (18) (19) and (13).
![]() (20)
(20)
This is in agreement with the corresponding expression in GSR.
3. Derivation of Time and Coordinate Expressions by Using Lorentz Transform
Using Lorentz transformation, the event at point ![]() in the frame
in the frame ![]() at a point
at a point ![]() is given to be according to Equation (7) by replacing
is given to be according to Equation (7) by replacing ![]() by
by ![]()
![]()
![]() (21)
(21)
Since the space is homogeneous it follows that
![]() (22)
(22)
Consider ampoule of light emitted from a source when the origins 0 and 01 are in coincidence at
![]()
In this care
![]() (23)
(23)
Substituting Equation (23) in Equations (22) and (21) yields
![]() (24)
(24)
![]() (25)
(25)
Inserting Equation (25) in Equation (24) yields
![]()
![]()
![]() (26)
(26)
With the aid of Equation (8) and Equation (10)
![]() (27)
(27)
When one consider the expression for the maximum speed in Equation (15), one gets
![]() (28)
(28)
It is very striking to observe that when no field exist, i.e. ![]()
![]() (29)
(29)
This is the usual SR expression.
For weak field
![]()
Therefore
![]()
Thus Equation (25) becomes
![]() (30)
(30)
This is the usual expression of GSR for a weak field.
4. Discussion
In Section 3 time dilation expression in the presence of any field has been derived by using mirror, see Equations (11) and (14). The only assumption which causes a limitation to this expression is the constancy of acceleration. The mirror motion is described by using Newton’s Law of linear motion with constant acceleration.
The speed of light is assumed to be constant. The resulting expression for ![]() reduced to that of SR in the absence of a field as shown by Equation (16) where
reduced to that of SR in the absence of a field as shown by Equation (16) where
![]()
It also reduced to GSR form for a weak field as shown in Equation (16).
The expression of length contraction has been obtained as well. Again this expression reduced to SR and GSR also [9] .
Lorentz transformation is also utilized to find a relativistic expression for ![]() and
and![]() . The expression shown in Equations (27)-(29) indicates that these expressions are similar to that obtained by the mirror method and are reduced to the corresponding SR and GSR expressions.
. The expression shown in Equations (27)-(29) indicates that these expressions are similar to that obtained by the mirror method and are reduced to the corresponding SR and GSR expressions.
5. Conclusion
The expressions for time and length obtained by using Lorentz transformation and using mirror clock, for fields at constant acceleration, and by assuming the speed of light to be constant indicate that GSR rests on a solid ground. It also indicates that space and time are affected by any field, not gravity only. Unlike the curved space- time derivation, where the field is assumed to be week, this derivation holds for strong fields as well. By reducing to SR and GSR for a weak field, it indicates its self-consistency.