1. Introduction
It is generally agreed in military and defence research circles that the older strictly hierarchical manner of organization of military forces and force design decision-making oriented around considering capability in terms of collections of platforms leave something to be desired. In particular, such arrangements make effective and fluid coordination between different force elements difficult at best and impossible at worst, and leave force design susceptible to overlooking both gaps and opportunities afforded by bringing functions housed within different platforms together. Historically, however, the ability to address these limitations of hierarchical, platform-centric structures has been retarded by a variety of factors, including education and training but particularly sharp limitations on the ability to communicate in operational settings. Modern communications, information and autonomous systems technologies seem to provide a basis for finally dissolving rigid crystalline military organizations to yield more flexible forces―better combined effects from heterogeneous capabilities, ability to adapt to rapidly changing operational circumstances, and less prone to cascading failure―by enabling close coordination horizontally across traditional structural boundaries. While the topic has been the subject of much theorizing (for instance, see [2] ), explanations have manifested deep methodological flaws with wide-reaching practical implications [3] [4] .
These problems with determining how to utilize the emerging technology to best effect, and just with explaining what this effect is and how it comes about, may be perhaps best seen in terms of the distinctions drawn between so-called “tame” problems and “wicked” problems [5] . Military theorizing has largely followed the pattern of long-established classical system engineering-type methods, which have proven successful in dealing with tame problems but which are also known to not generalist adequately to problems that manifest incomplete and contradictory requirements, non-stationarity, complex interwoven interdependencies, unpredictability of future states, and are effectively unique.
Yet these considerations are nothing new: even the founding intellectuals of the Military Enlightenment understood war and battle as manifesting complex, messy phenomena and thus grappled with what this means for rational theory development. The two main figures of the period differed considerably in their subsequent answers. Jomini [6] established the search for a universal theory of war and battle, which has been dominant in military thinking ever since. Jomini’s recognition that not everything is predictable and tame and thus not everything will fit into such a theory resulted in his splitting the domain of the complex and uncertain away from rational theory; this split between the “science” of war, dealing in certainties, from the “art” of war, dealing in the ambiguous, messy and uncertain, continues to haunt the field to the present. Clausewitz [7] denied the existence of such a fixed universal theory and emphasized instead problem solving method for dealing with what we now call wicked problems.
Against this backdrop, we developed the TCW model [1] , comprising a generalized tensorial union of the classical Lanchester-Osipov combat equations [8] [9] [10] ) and distributed C4ISR systems, towards a combat model able to capture the basic notion of collaboratively oriented and functionally individuated networked military forces, under the broad aim of capturing some of the features of uncertainty in a formal model that have proven so challenging to model in the past. In this paper, we extend this formalism with using entropic Lie-derivative to advance the representation of uncertainty in our approach, and to capture the notion of symmetry in warfare; opposing forces that are widely different in composition, strategy and operating methods are said to be asymmetrical.
2. Review of the Tensor Combat Model
The basic attrition equations include two forces, Red/Attacker’s strength:
and Blue/Defender’s strength:
, governed by two basic types of dynamics:
1) Lanchester square law:
(1)
(where
and
denote individual combat-rate coefficients for the Red and Blue forces, respectively); and
2) Lanchester linear law:
(2)
(where
and
denote mixed combat-rate coefficients)
In our first paper [1] , we generalized and combined Lanchester Equations (1)-(2) while seeking to capture the broadly agreed theme of contemporary military thinking, which seeks to provide a highly distributed C4ISR system, where information can be readily shared and distributed.
The basic TCW development in [1] was also motivated by the recent paper by McLemore et al. [11] , so both system inputs and outputs are comparable with inputs and outputs of the Air Campaign Scenario simulation presented in [11] . Our scaled-down 9 aircraft system input is formulated in standard fashion. Our Red forces are given by a Bipartite graph including 4 Fighter aircraft and 5 Sensor aircraft (see Figure 1 in [1] ), and our Blue forces are given by a Tripartite graph including 3 Fighter aircraft, 3 Sensor aircraft and 3 New aircraft (see
![]()
Figure 1. Sample simulation of the basic tensor combat Equation (4) for 10 time units with random initial conditions: monotonic dynamics of Blue forces.
Figure 2 in [1] ).
The Red and Blue aircraft configurations are defined by the adjacency matrices (with the local feedback-loops):
From the adjacency matrices
and
the corresponding combat-tensors1 are defined as:
![]()
Figure 2. Sample simulation of the basic tensor combat Equation (4) for 10 time units with random initial conditions: monotonic Red-Blue phase plots.
here
and
are Power tensors with 9 × 9 components defined by the bell-shaped spatiotemporal
functions, implemented in Mathematica as:
In this way constructed Red and Blue combat-tensors
and
still retain the configuration of zeros in the adjacency matrices
and
, with ones replaced by the random-weighted Sech-functions (which are here, for simplicity, only temporal, not spatial, so we remain within the ODE-framework; see discussion in subsection 4).
3. TCW Stage: Battle-Manifold with Dynamics of Vector and Tensor Fields on It
3.1. The Battle-Manifold
Both in geometrical dynamics of natural complex systems [12] [13] [14] and in modern autonomy of sociotechnical complex systems [15] , a set of all active and controllable degrees-of-freedom (DOFs), with some additional geometric conditions, of an arbitrary complex system comprises the configuration manifold2 for that system. Following this fundamental manifold prescription, any battlespace (see [16] and the references therein) in TCW can be formally defined as the battle-manifold, or its subset―the battle-submanifold.
Two simple examples of autonomous battle-submanifolds are (see [12] ):
1) A 3D configuration manifold of a simple UGV:
, coordinated by
;
2) A 4D configuration manifold of a car:
with
, where
is the group of rotations in the Euclidean plane
, coordinated by
.
Two more complex autonomous submanifolds are (see [12] ):
3) A 15D configuration manifold for an artificial hand (only flexion/extension in
all three joints of all fingers) is defined as the Cartesian product:
;
4) An nD configuration manifold for a humanoid robot is the set of all movable
joint angles, defined as the Cartesian product:
of n rotational
-groups for all joints, where
is the group of rotations in
.
We give two examples of more realistic battle-submanifolds.
・ A 3nD human socio-political manifold
, representing a generic social game played among n bargaining agents, according to Bueno de Mesquita’s socio-political models (see [17] for a recent review), can be formally defined as:
Similar configuration manifolds might be constructed for financial markets, multinational companies, political and military coalitions, and trade consortiums.
・ A 6nD robotic cyber-physical-cognitive manifold
, representing a dynamic configuration of a generic swarm of cyber-physical-cognitive robots, is defined as:
where each robot is mechanically defined as the Euclidean group
of rigid motions in
(consisting of translations and rotations in
; see [15] and the references therein).
The union of a large number of similar submanifolds can form a realistic battle-manifold. In case of a very large battle-manifold Mn, it can be approximated with
, where n, the total number of DOFs, can be in millions (using computational framework outlined in the Appendix).
Complex warfighting dynamics on such battle-manifolds is naturally defined as an interplay of spatiotemporal vector and tensor fields flowing on them (see [1] ).
3.2. Warfighting Actors: Vector and Tensor Fields on the Battle-Manifolds
On any battle-manifold Mn we can observe a dynamic interplay of various Actors, all defined by various vector and tensor fields, depending on their complexity.
Simpler Actors are formally defined as spatiotemporal vector-fields,
, similar to velocities and forces from classical mechanics, or flow-velocities and vortices from fluid mechanics, or Hamiltonian vector-fields from generalized mechanics [12] [18] , or Hopfield-Grossberg vector-fields from neurodynamics [19] .
The main Actors on any battle-manifold Mn are the Red and Blue vector-fields,
and
, respectively, which represent either the Red-Blue populations, or any other power measure of the Red-Blue forces.
More complex supporting Actors on Mn are defined as various spatiotemporal
tensor fields (tensors, for short):
of different orders
(or tensor ranks).
The supporting warfighting tensors may include:
1) 2nd-order tensors, similar to metric/inertia tensors from mechanics, or stress and strain tensors from elasticity, or stress-energy tensors from electrodynamics and gravity; other 2nd-order tensors are usually constructed directly from vector-fields, either as their outer products, or as their gradients:
.
The main supporting Actor is the combat-tensor
, defined earlier, which belongs to this category;
commutes with any other 2nd-order tensor field of the same covariance on the same battle-manifold Mn (e.g.
)―they can be added together as linear machines:
2) More complex, fourth-order tensors, similar to the Riemann curvature tensor,
, as well as various tensors from thermo-visco-elasto-plasticity.
All these tensor fields are spatiotemporal dynamical objects. Using time derivatives and Lie derivatives of these tensor fields, we will construct various generalizations of the Lanchester combat equations.
4. Tensor Combat Equations
As already mentioned, we assume the simple 9D battle-manifold
, coordinated by
, although all the calculations would equally work for any manifold dimension (up to millions, using the computational framework outlined in the Appendix). We start the TCW modeling with the tensor Lanchester square law, which is the following vector/tensor generalization of Equation (1):
(3)
where the Red and Blue forces are then defined as vector-fields,
and
, and their effectiveness coefficients are denoted by k and κ. The tensor fields
and
represent the sum of their combat-tensors (
and
), their total power (or stress-energy) tensors (
and
), and the Red and Blue swarming matrices,
and
from [11] (provided the swarming matrices have dimension of
):
All tensor calculations in this paper are derived using Mathematica® tensor package xTensor [20] 3.
Assuming, for simplicity, the coordinate independence (
), both sets of expanded Lanchester equations represent sets of coupled nonlinear ODEs, which can be directly numerically solved, for any given Red and Blue initial conditions:
,
, using any adaptive Runge-Kutta ODE-solver (e.g. Cash-Karp, Fehlberg and Dormand-Prince integrators), or their corresponding manifold/Lie-group integrators (e.g. Runge-Kutta Munthe-Kaas).
In the general case of explicit coordinate dependence (
), we would be actually dealing with the set of the first-order nonlinear PDEs, which would all require spatial discretization (e.g., using the Method of Lines, as implemented in Mathematica), after which the above mentioned ODE-solvers can be used again.
The same computational algorithms will apply, in both cases (ODEs and PDEs), also for the extended tensor Lanchester equations, formulated as follows.
Next, to include the Lanchester linear law Equation (2) into Equation (3), while keeping their covariance (so that each term represents a vector-field), we need to extend them with quadratic terms of the Lanchester unaimed-fire equations (linear law) as:4
(4)
where the fourth-order tensors
and
represent more complex, strategic, tactical and operational, Red and Blue capabilities, which can be defined either as the outer products of various matrices from [11] , or composed as triple tensor sums:
(5)
For our readers’ convenience, we replicate here the sample simulation (see Figures 1-3) of the tensor Lanchester combat Equation (4) performed in Mathematica
![]()
Figure 3. Sample simulation of the basic tensor combat Equation (4) for 10 time units with random initial conditions: monotonic dynamics of Red forces.
for 10 time units (to match the simulations given in [11] ) and random initial conditions.
Interpretation of this simulation and comparison with the results reported in [11] are given in [1] . Briefly, Red (bipartite) is loosing (Figure 3), Blue (tripartite) is winning (Figure 1), and all individual conflicts are concentrated in the left-upper corner of the phase-plane (Figure 2).
5. Modeling Uncertainty and Symmetry of Warfare: From Clausewitz to Entropic Lie Derivative
In this section, we propose a Clausewitz-type warfare uncertainty principle at work [7] , which is, in spirit, akin to the fundamental Heisenberg uncertainty principle in quantum mechanics. Unlike Heisenberg, Clausewitz did not have the mathematical tools available at the time, or even the language to describe the full warfare complexity at times, but he definitely grappled with uncertainty in war and battle as his most fundamental core intellectual construct. The nature of this uncertainty amounts to the consequences of Gödel’s incompleteness phenomena in mathematical logic and its real-world applications, meaning that it is due to the presence of (often hidden or disguised) logical paradoxes. Mathematically, the hidden nature takes the form of fixed-point solutions in axiomatic formulations, but it is not difficult to relate them directly with paradoxes long studied in philosophy. It happens whenever we have the potential for self-reference, which is basically any time we don’t assume a mathematically “trivial” system. In our view, both Clausewitz- and Heisenberg-type uncertainties are the outcome of a set of Gödelian paradoxes, arising in the theory because of the built-in possibility of self-reference: one effects the result of the observation by the making of the observation because it is set up from the start with the notion that one is observing from within the system, not peering into it from outside. This notion of hidden self-reference in quantum mechanics is also quite close to the way in which Clausewitz conceived of his uncertainty. The rest of Clausewitz’s work is about how to both deal with it on the one hand in terms of avoiding exposure to the worst kind of failures one does not want to happen, and how to take advantage of it through the opportunities it proves, on the other.
Regarding the warfare symmetry, we remark that the scalar Lanchester models, (1)-(2), are symmetric, i.e., automorphic under a swap of R and B variables5. In our general warfare modeling, it is important to properly address the warfare symmetry issue, which we present in this section.
5.1. Entropic Lie-Derivative Machinery
The Lie derivative operator, denoted by
is the simplest tensor derivative (see Appendix for technical details) on any smooth manifold M, which does not require connection (or, any other geometric structure) on the manifold (see [12] [18] and the references therein).
generalizes two familiar cases from mechanics and nonlinear control: the directional derivative of a scalar function (i.e., scalar field) along a vector-field and the Lie-bracket commutator of two vector-fields6.
For an arbitrary geometric/physical object, T, or specifically, any
-tensor field
, its Lie derivative,
, along the flow7 of a
certain vector-field
, measures in what degree the geometric object T moves along with the flow of va (i.e., allows for the “ Lie dragging” along the flow of va), or resists to move with the flow of va (i.e., resists the Lie dragging).
This notion of Lie dragging with/without resistance represents the core concept for our modeling of complex warfighting under uncertainty. Physically speaking, it is related to Prigogine’s entropy S of any open non-equilibrium thermodynamical system, which considers irreversible systems/processes that exchange both energy and matter with their environment. Prigogine’s Extended Second Law of Thermodynamics (see [24] [25] ) formally reads:
The Lie-bracket commutator is defined by the antisymmetric bracket
, which measures the degree of non-commutativity of the Red-Blue composed flows:
1)
: flowing first along the Red flow (in which Blue is
dragged by Red) and then along the Blue flow (in which Red is dragged by Blue), versus
2)
: flowing first along the Blue flow (in which Red is
dragged by Blue) and then along the Red flow (in which Blue is dragged by Red).
The commutator is formally defined as:
In case the Red and Blue vector-fields do commute, their Lie-bracket commutator is zero and the corresponding entropy is conserved:
In addition, the
-commutator is associative:
Its straightforward interpretation is that, all other quantities being equal, at each phase of warfighting: whoever strikes first has the advantage, and the opponent is
left to play the catch-up game. Therefore, the
-commutator effectively decides who wins and who loses at each phase of warfighting.
More generally, the
-commutator defines the Lie algebra of all
possible vector-fields on the battle-manifold M, which satisfies the (circular) Jacobi identity:
where
is an independent third-party vector-field (like e.g., United Nations).
The above linear and quadratic tensor Lanchester Equations (4) are extended
with the
-commutators as:
(6)
which address the warfare symmetry. In case of nonzero
-commutators,
and
, given their potentially decisive role in the warfare, we consider Equation (6) as the first realistic TCW model.
The spatiotemporal Red and Blue vector-fields,
and
, respectively, are implemented in Mathematica as:
Their Lie-bracket commutator is defined (from scratch) via Jacobian matrix, using the following functional definitions:
In such a way defined commutators are applied to the Red and Blue vector-fields as:
CommutRB = LieBrc[RedVec, BlueVec, X],
CommutBR = LieBrc[BlueVec, RedVec, X].
In our specific simulation case, both commutators evaluate to the 9-component zero vectors. Obtaining zero commutators means that we are dealing with the symmetric warfare. This also implies that the simulations of the basic tensor combat-Lanchester equations would not change.
5.3. Entropic Lie-Dragging of Combat, Strategic, Tactical and Operational Objects
Given this basis, we can explore general Lie-dragging of the opposite side combat-tensors, as well as arbitrary strategic, tactical and operational objects along the Red and Blue vector-fields. We begin with the Red and Blue combattensors,
and
, respectively. Their Lie-dragging by the opposite side vector-fields is defined as:
and measures the degree of resistance of the opposite side sensor/computer networks. In case of nonresistance, these equations reduce to:
Including the Lie-dragging of the opposite side networks into the tensor Lanchester equations with [Red-Blue]-commutators (6), gives the following more realistic warfighting system:
(7)
where the Lie-dragging terms (
and
) are multiplied by the Red and Blue vector-fields (as
and
terms) to preserve the covariance of the tensor equations.
The Lie-dragged combat Equation (7) represent the realistic TCW model that we have been looking for, the general model which generalizes the Lanchester combat equations under a networked force view of military command arrangements, and also address warfare symmetry and captures a notion of the deep uncertainty of military operational situations. Equation (7) are implemented in Mathematica using the following two-step process.
1) Lie-Dragging of the opposite side combat-tensors is computed using the xTensor package [20] as follows:

2) The temporal tensor combat Equation (7) are implemented as follows:
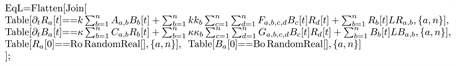
A sample simulation of this initial-value problem for 10 time units with random initial conditions is given in Figures 4-6.
Comparing the Lie-dragged simulation (Figures 4-6) with the basic tensor combat dynamics (Figures 1-3) shows the subtle control action of the Lie-dragging effect on the overall combat Red-Blue dynamics. Specifically, Red (bipartite) forces are still loosing (Figure 4), with double amplitude. Blue (tripartite) forces are still winning (Figure 5), with double amplitude. All individual conflicts transparent in the phase plane are still present, now with double amplitude and spread uniformly along the diagonal of phase-plane (Figure 6), while in the initial tensor combat dynamics they were concentrated in the left-upper corner of the phase plane.
Finally, we consider the Lie-dragging of more complex strategic, tactical and operational (STO) objects, similar to
and
tensors given by Equation (5), belonging to the Red and Blue sides and defined by the new (3,1) tensors,
and
, respectively (also composed as triple tensor sums:
). Their Lie-dragging by the opposite side vector-fields is defined as:
and measures the degree of resistance of the opposite side STO objects. Again, in case of nonresistance, these Eqs. reduce to:
and
Including the Lie-dragging of the opposite side STO objects into tensor Lie-Lanchester Equation (7) gives the following even more realistic warfighting system:
![]()
Figure 4. Sample simulation of the tensor combat Equation (7): time evolution of the Red forces Ra for 10 time units and random initial conditions.
![]()
Figure 5. Sample simulation of the tensor combat Equation (7): time evolution of the Blue forces Ba.
![]()
Figure 6. Sample simulation of the tensor combat Equation (7): Red-Blue phase plot.
where, as before, the Lie-dragging terms (
and
) are multiplied by the Red-Ra, Blue-Ba and third party-Ea vector-fields (as
and
terms) to preserve the covariance of the tensor equations, so that each term still remains the vector-field.
6. Conclusions and Future Work
We have extended the basic tensor-centric warfare, developed in [1] as a generalized tensor union of classical Lanchester equations under the modern notion of utilizing information and communications networks in military operations to enable greater collaborative decision-making across previously acicular hierarchical command arrangements. The extension to an entropic Lie-derivative provides a stronger notion of the uncertainty inherent in battle, and describes formally the notion of symmetry in war.
Future work will examine more complex tensors, including high-dimensional Dirac-delta functions for modeling various delta-strikes and missiles, as well as tensors for learning with adoptions from deep learning/TensorFlow, and tensors of quantum origin, such as tensors from quantum computation and quantum graphs. Our research direction is motivated by the need for more realistic analytical combat models. We feel that the limited applicability of classical Lanchester-type models is less due to the limitations inherent to constructing formal models using a few idealized parameters and more to do with the intention of the model to provide predictions about combat outcomes. In other words, development of new formal combat models of greater utility hinges on the choice of problem that motivates the model in the first place; in place of earlier intentions to analytically predict outcomes, our research direction is oriented around trying to determine the uncertainty of outcomes, and particularly, to make predictions about the uncertainty or variability of outcomes for blue and red, where uncertainty is here taken in an entropic sense. We also intend to develop a richer lexicon of outcomes against which to make such entropic estimates.
The reason this matters is that decision-making under uncertainty is oriented around uncertainty with respect to failure outcomes: blue wants to steer away from uncertainty with respect to failure outcomes for blue, but towards uncertainty around failure outcomes for red, and vice-versa. In terms of our modeling, we thus consider decision-making of the opposing forces to be a matter of control.
Acknowledgements
The authors are grateful to Dr. Tim McKay and Dr. Brandon Pincombe, Joint and Operations Analysis Division, Defence Science & Technology Group, Australia for their constructive comments which have improved the quality of this paper.
Appendix: Computational Framework
Persistent Homology Algorithms
A network-computational framework, with networks/tensors of up to millions of nodes, can be developed using the publicly available Matlab® toolbox supporting the cutting-edge topological research of brain cliques and cavities from computational neuroscience (the Blue Brain project [27] [28] [29] ). It is based on the persistent homology algorithms on directed simplices [30] .
General Lie Derivative Calculations
For its definition, the Lie derivative
requires only the vector-field
along which an arbitrary tensor T would flow or would resist the flow (i.e., would be “dragged” or would resist the “dragging” ). For most tensors,
is
naturally expressed in terms of the gradient operator,
, for
. Only in case of high-order exterior differential forms, a more natural/elegant would be
expression in terms of Cartan's exterior derivative d (see [12] [18] and the references therein).
The following computations of the Lie derivative
for all possible tensors T up to the order 4 are derived using the fast tensor package xTensor [20] for Mathematica®:
a) The Lie derivative of a scalar field/function
along the vector-field
is its directional derivative, i.e., the inner product of the gradient
and the vector-field
:
For a pair of scalar fields/functions
, the following two relations hold:
・ The Leibniz rule:
and
・ The linearity relation:
These two rules can be extended to higher-order tensors.
b) The Lie derivative (along the vector-field
) of another vector-field
is their Lie bracket
(or, commutator), which is yet another vector-field, given by:
and measures how non-commutative the composed flow is (i.e., first flowing down the one vector-field and then flowing down the other one), since in general
.
The space of all vector-fields
forms a Lie algebra with respect to the Lie bracket
. This Lie algebra satisfies the Jacobi identity:
For any
-tensor field
, the following Lie-algebra representation holds:
c) The Lie derivatives of the second-order tensor fields on M (these are the most common tensors, like the stress and strain tensors in elasticity, Maxwell tensor in electrodynamics, etc.) are defined as:
In case of the covariant (0, 2)-tensor field
we have:10
・ In case of the mixed (1,1)-tensor field
along
we have:
・ In case of the contravariant (2, 0)-tensor field
we have:
d) The Lie derivatives of low-dimensional differential forms (i.e., completely asymmetric covariant tensor fields obeying Cartan’s exterior calculus) are given by:
・ In case of the 1-form
(e.g., the canonical form of a Hamiltonian system) we have:
・ In case of the closed 2-form
(e.g., the symplectic form of a Hamiltonian system) we have:
where
denotes the asymmetric part of
.
e) The Lie derivative of a general exterior p-form
(e.g., exterior forms used in Hodge-de Rham theory) along
is defined in the coordinate-free form by “Cartan’s magic formula:”
More generally, for any Killing vector-field
and any conserved, symmetric (0,2)-tensor field
, we have:
.
Here
is the exterior derivative, which commutes with the Lie derivative:
which in case of scalar functions (or, 0-forms) becomes:
is the contraction of the p-form ω and the vector-field
, which also commutes with
. In case of a scalar field/function
, Cartan's formula simplifies as:
f) The Lie derivatives of the third-order tensor fields on M (which are gradients of the above second-order tensors and the strain gradients in micromorphic elasticity, etc.) are defined as:
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
g) The Lie derivatives of the fourth-order tensor fields on M (e.g., the Riemann and Weyl curvature tensors in gravity and the compliance and stiffness tensors in elasticity) are defined as:
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
・ Given a
tensor-field
, its Lie derivative
is given as
h) In general, for a pair of arbitrary tensors
, the Leibniz rule holds:
In case that both tensors have the same rank,
, the linearity relation also holds:
All possible Lie-derivative expressions can be derived using the tensor package xTensor [20] for Mathematica.
After Mathematica derivation, all tensor expressions can be completely evaluated (for manifolds of any dimension) using quasi-symbolic gradients computed by automatic differentiation, implemented either in C++, or in functional languages like Haskell (AD library) [31] and/or F-sharp (DiffSharp library) [32] .
1A more formal definition of the combat-tensor can be given as follows. Recall that a metric graph (possibly with feedback loops) is a graph
such that:
・ Each edge
is assigned a finite length
;
・ The edge e is identified with the interval
; and
・ A dynamic coordinate
is associated with each edge
, so that
.
Any defence sensor, communications and information system network can be defined by the adaptive connectivity matrix of a metric graph:
The weights
are trainable by Hebbian, backpropagation, or deep learning, thus making
into a neural network.
The combat-tensor is now formally defined as a linear combination of a number of connectivity matrices of various operational networks (communications, sensors and information systems, etc.):
where the last term introduces Einstein’s summation convention over repeated indices.
2Informally, a smooth manifold Mn is a smooth nonlinear n-space which is locally (at each point) equivalent to the linear Euclidean n-space
. Formally, Mn is defined via compatible Euclidean charts:
for all points
and comprising a smooth atlas (for technical details, see [12] [18] and the references therein).
3Similar calculations could be performed also with other tensor packages, like ccgrg [21] .
4The Basic Red and Blue tensor combat Equations (3)-(4) are valid for any linear/flat manifold M9. In case of a strongly nonlinear/curved manifold M9, they would need the additional connection coefficients (i.e., Christoffel symbols)―which can be neglected for our purpose, as an unnecessary over-complication. With this view in mind, in the following sections we will introduce more complex dynamics and nonlinear control concepts into Equations (3)-(4), without introducing any geometric connection (e.g., Levi-Civita connection on Riemannian manifolds)―which can always be added to the battlespace system as additional nonlinear complexity (see [13] ).
5For example, the scalar Lanchester models (1)-(2) can be seen as special cases of the non-symmetric Lotka-Volterra predator-prey model (see [22] ):
6For a popular visualization of the Lie derivative, see Figs. 14.13-14.16 in [23] .
7From the fluid-dynamics perspective (where
is called the Liouville operator), a vector-field va is an infinitesimal generator of its flow
and the flow
is an integral curve of its vector-field va. From the dynamical-systems perspective, the vector-field (e.g., Hamiltonian vector-field) is defined by the set of ordinary differential equations (e.g., Hamiltonian equations of motion), and its flow is the solution for some initial conditions. The existence of the flow for some vector-field is insured by the existence theorems for differential equations. See next footnote for additional technical details.
where
is the internal entropy production within the system, and
(=0 for an isolated system) is the external entropy flux (due to the exchanges with the environment).
The non-equilibrium thermodynamics has the following Lie-derivative analogy:8
Lie dragging with resistance:
: growth of entropy; and
Lie dragging with nonresistance:
: conservation of entropy, from which we can infer that the warfare uncertainty, as measured by the non-equilibrium entropy, grows with resistance; when resistance stops, the warfare uncertainty stays constant.
More precisely, this Lie-entropy analogy can be geometrically interpreted as: whenever we have resistance of the opposite side, we are dealing with a positive Lie derivative of the associated geometric object9, i.e.,
, which means that the non-equilibrium entropy of the underlying open system is growing, therefore the warfare uncertainty is growing. Otherwise, when the Lie derivative is zero, i.e.,
, that means the underlying entropy is conserved and the warfare uncertainty remains constant.
As an introductory example, consider an abstract warfare scenario where some sociopolitical force, represented by the vector-field A, is dragging (either physically, or psychosocially as a “ threat” ) another sociopolitical structure of arbitrary complexity, represented by the general tensor field B (which can be another force, or another sociopolitical organization, etc.). This scenario is formally written as the Lie derivative
. So long as B is resisting, we have
, and correspondingly:
. When resistance stops, it becomes:
, and correspondingly:
.
5.2. Measuring Warfare Symmetry: The [Red, Blue]-Commutator
An important particular case of the general Lie-derivative,
, is the
commutator,
, also called the Lie-bracket, between the Red
vector-field
and the Blue vector-field
, which determines the global warfare symmetry.
8Strictly speaking, these relations are formally valid only for positive-definite tensors (i.e., when the tensor expression
is positive definite). In general, they hold for their corresponding absolute values:
Lie dragging with resistance:
: growth of entropy; and
Lie dragging with nonresistance:
: conservation of entropy.
In other words,
. Also, our “Lie dragging with nonresistanc” is in geometrical literature usually called the “Lie transport.”
9Such a thermodynamics analogy is not unique for our approach. In the specific framework of Riemannian geometry, there is the so-called Ruppeiner metric, defined as a (negative) Hessian of the entropy function [26] . Since we are working in a more abstract, metric-free framework, such a metric is not required. However, if our future work requires specializing to a Riemannian battle-manifold, its metric will naturally be the Ruppeiner metric.
10In particular, on a Riemannian manifold M, the Killing vector-field
has the property that Lie differentiation with respect to it annihilates the Riemannian metric
:
If the flow
is a one-parameter group of isometries on M:
, the vector-field
which generates
, is a Killing vector-field. The necessary and sufficient condition for
to be a group of isometries is:
. Consequently, the necessary and sufficient condition for
to be a Killing vector-field is that it satisfies Killing’s equation:
or
.