1. Introduction
Kinematics, including multiple trajectories of a bouncing massive point-like particle on a vertical plane thrown at an angle with respect to a horizontal surface is a classic physics problem [2] . The point-like character of the object i.e. the lack of its size suppresses the impact of its internal degrees of freedom, e.g. spin, on kinematics. We depart from this stepping stone scenario and consider a generalization where a point-like object is replaced with a round shaped entity such as a solid and/or a hallow ball or a short length cylinder. The spin adds interesting features to the kinematics. For instance a free falling spinning object upon impact with a horizontal surface bounces multiple times drifting away from the points of impacts. As we were developing the mathematics of the problem auxiliary quantities such as: run-time between adjacent bounces, sensitivity of the range between sequential bounces and etc. were calculated as well. The general features of these analyses are summarized in a Mathematica based simulation program making the analysis robust providing opportunities exploring the “what if” scenarios. This note is composed of three sections. In addition to Motivation and goals, in Sect. 2 we develop the needed physics solving the problem. This section also embodies analysis and output. Section 3 is the conclusions and closing remarks.
2. Physics of the Problem and Its Solution
Figure 1 depicts the scenario at hand. A solid ball of mass m, size r and clockwise spin ω about the horizontal axis through the center is held, h, distance away from a horizontal reflecting surface. The ball is dropped freely, as it falls the only active force on the ball is the weight that passes through the center; this preserves the spin from the point of release to the impact, as shown.
At the impact the floor imparts three different effects: 1) it reorients the initial downward vertical velocity in a slanted upward direction 2) because of surface roughness it generates a horizontal impulse drifting the ball along the horizontal, specifically, it pushes the ball along the opposite direction of the orientation of the angular velocity at the impact, x-axis as shown in Figure 2(b) and 3) the surface roughness slows the spin. These are depicted in Figure 2.
It is intuitive to say that right after the bounce because gravity is the only active force acting on the ball the center of the ball would trace a parabolic trajectory. Furthermore, because of the same reason the spin of the ball stays the same; its angular momentum conserves. One may also extend the aforementioned conclusions for all subsequent multiple bounces the number of which is determined by the restitution factor, e.
With this intuitive insight to quantify the kinematics we formulate the problem.
We write the dynamic version of the Newton’s law as,
![]()
Figure 1. A spinning ball held at rest from a reflecting surface.
![]()
Figure 2. (a) depicts the ball at impact. (b) is the situation right after the impact.
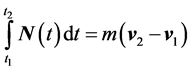 , (1)
, (1)
where 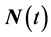 is the floor reaction and is perpendicular to the interface. Symbolically speaking the time span,
is the floor reaction and is perpendicular to the interface. Symbolically speaking the time span, 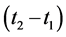 , is the contact time of the ball-floor and its value depends on the value of e. For the analysis of the problem on hand its value doesn’t come in the play. The
, is the contact time of the ball-floor and its value depends on the value of e. For the analysis of the problem on hand its value doesn’t come in the play. The 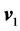 and
and 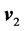 are the corresponding velocities right before and after the impact, respectively. By projecting Equation (1) along the x-axis and replacing the integrand with
are the corresponding velocities right before and after the impact, respectively. By projecting Equation (1) along the x-axis and replacing the integrand with 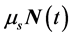 i.e. the maximum static friction we identify the cause of the horizontal push. In this scenario the RHS of Equation (1) is,
i.e. the maximum static friction we identify the cause of the horizontal push. In this scenario the RHS of Equation (1) is, 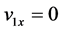 and momentum of the drifted bounced ball is mv2x. Accordingly, Equation (1) along the x-axis is,
and momentum of the drifted bounced ball is mv2x. Accordingly, Equation (1) along the x-axis is,
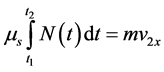 , (2)
, (2)
one may realize the integral on the Left Hand Side (LHS) is the linear impulse along the y-axis. Note also the orientation of the static friction shown in Figure 2(a) is the cause of spin retardation. Its impact is given via angular impulse. Writing Equation (1) for the torque and related angular momentum gives,
 , (3)
, (3)
where 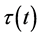 is the torque, so that the LHS is the angular impulse, where Icm is the moment of inertia of the rotating object about the center-of-mass (cm) and ω’s are the associated spins, i.e. angular velocities. Applying Equation (3) to the case on hand replaces the integrand with
is the torque, so that the LHS is the angular impulse, where Icm is the moment of inertia of the rotating object about the center-of-mass (cm) and ω’s are the associated spins, i.e. angular velocities. Applying Equation (3) to the case on hand replaces the integrand with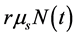 , yielding,
, yielding,
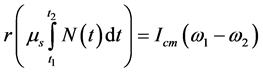 , (4)
, (4)
Substituting Equation (2) in (4), gives,
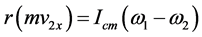 , (5)
, (5)
Furthermore, while the ball is in contact with the floor and rolls without slipping we apply,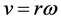 . Specifically, for the problem on hand the horizontal component of the velocity, v2x, right after the bounce is subject to
. Specifically, for the problem on hand the horizontal component of the velocity, v2x, right after the bounce is subject to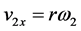 . Substituting this in Equation (5) we get,
. Substituting this in Equation (5) we get,
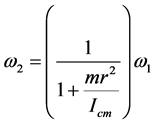 , (6)
, (6)
Accordingly, we realize the explicit relationship between the spins before and after the impact; i.e., ![]() , meaning 1) the bounced ball spins slower after the impact and 2) its positive value shows that after the impact it doesn’t change its spin direction―in the shown figure it preserves its clockwise spin. The moment of the inertia about the center-of-mass, Icm, may be substituted as
, meaning 1) the bounced ball spins slower after the impact and 2) its positive value shows that after the impact it doesn’t change its spin direction―in the shown figure it preserves its clockwise spin. The moment of the inertia about the center-of-mass, Icm, may be substituted as
![]() . Depending to the character of the object on hand, e.g. a solid sphere, a hallow sphere or a short cylinder about its axial axis, γ, is known. These are γ = 2/5, 2/3 and 1/2, respectively. Substituting for Icm, Equation (6) yields,
. Depending to the character of the object on hand, e.g. a solid sphere, a hallow sphere or a short cylinder about its axial axis, γ, is known. These are γ = 2/5, 2/3 and 1/2, respectively. Substituting for Icm, Equation (6) yields,
![]() . (7)
. (7)
its value for a solid ball is,![]() . That is a free falling solid sphere irrespective of the mass, size and the initial height, h, upon impact loses 71% of its spin.
. That is a free falling solid sphere irrespective of the mass, size and the initial height, h, upon impact loses 71% of its spin.
In general the ball bounces more than once. Following analysis similar to the aforementioned reveals the subsequent bounces don’t alter the spin other than the first bounce; i.e. the spin given by Equation (7) stays the same. This is justified according to Equation (5). For a multiple bounce it reads,
![]() , (8)
, (8)
where i and f indicate the “initial/before” and “final/after” states. For a rolling ball we substitute ![]() and
and![]() , Equation (8) yields,
, Equation (8) yields,![]() . Meaning the static friction doesn’t do mechanical work and preserves the spin. This is the same conclusion that one draws analyzing the states of a rolling ball on a rough horizontal surface. An auxiliary outcome of this observation is the equality of the horizontal velocities between the multiple bounces. However, because the runtimes between the bounces dependent on the restitution factor, e, their associated range, i.e. the horizontal traveled distances between adjacent bounces differ. Perfect elastic collisions with
. Meaning the static friction doesn’t do mechanical work and preserves the spin. This is the same conclusion that one draws analyzing the states of a rolling ball on a rough horizontal surface. An auxiliary outcome of this observation is the equality of the horizontal velocities between the multiple bounces. However, because the runtimes between the bounces dependent on the restitution factor, e, their associated range, i.e. the horizontal traveled distances between adjacent bounces differ. Perfect elastic collisions with ![]() result identical range.
result identical range.
For instance, the runtime between the first and the second impact is,
![]() .
.
During this time interval![]() . Combining the latter two expressions with Equation (7) yields,
. Combining the latter two expressions with Equation (7) yields,
![]() . (9)
. (9)
Its value for a solid ball with ![]() is,
is,![]() . Without proof this is
. Without proof this is
mentioned in [3] .
Having considered the aforementioned information we derive analytic equations describing the trajectories of a spinning bouncing ball. In the coordinate system depicted in Figure 2, after the first bounce because the gravity is the only active force the center of the ball traces a parabolic trajectory [2] ,
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() . (12)
. (12)
In these equations g is the gravity, the takeoff speed after the first impact is v2, the projectile (reflected) angle is θ, h is the initial height and the restitution factor is, e.
Utilizing this information we craft a Mathematica code simulating the features of a spinning bouncing elastic ball. Accordingly, as shown in Figure 3 for two chosen values; h = 3.0 m, and e = 0.7 with two control sliders we adjust the initial spin, ω, and the number of the bounces with the t-slider. A real-life animation of this program traces the bounces according to the running “ω clock” depicted with the pink disk-clock and its single arm. This figure shows the characters of a bouncing ball with e = 0.7. Running the program with e = 1 results multiple parabolas with the same heights.
Auxiliary information about the quantities of interest such as range, Equation (9), for a chosen initial spin ω vs. the number of the bounces is shown in Figure 4. With this program one has the capability of simulating the sensitivity of the range as a function of ω.
For instance as shown, a spinning ball with ω = 9 rad/s dropped form a 3.0 m height drifts 27.9 cm between the first and the second impact; 19.6 cm between the second and the third and etc.
Figure 5 shows the variation of the reflecting angle θ vs. spin value ω. Equation (12) is used plotting this graph. One might have intuitively expected this; however, this graph quantifies the output. The initial heighth, e factor and γ used in this plot are, 3 m, 0.7 and 2/5, respectively.
Figure 5 shows the fast spin corresponds to a smaller reflection angle and visa-versa. For instance, a slow spinning ball with ω = 10 rad/s ~ 100 rev/min bounces almost vertically. Yet, a fast spinning ball with ω = 100 rad/s ~ 1000 rev/min reflects at 62˚ with respect to horizontal.
![]()
Figure 3. Snap shot of characteristics of a spinning ball dropped freely from a height h = 3.0 m.
![]()
Figure 4. Plot of the range vs. number of the bounces for a chosen e value; here e = 0.7.
![]()
Figure 5. Display of the bounced angle θ vs. the spin ω.
3. Conclusion
Linear impulse and angular impulse are useful applied mechanical quantities, yet their applied mathematical models quantifying their applications are somewhat hindered in the literature. In a real-life situation one may encounter cases such as, dribbling a spinning basketball or throwing a spinning tennis ball on a floor. Mathematical challenges analyzing these kind of problems stem mainly from the size of the object. In elementary scenarios, the size is ignored suppressing the degrees of freedom reducing the problem to analysis of point-like objects. Reference [3] has posted the problem of a spinning ball as a challenging problem with no solution. The scope of the posted problem is limited to only one bounce! In our investigation we augmented the problem by considering multiple bounces. First we are posting the solution, and in addition have crafted a simulation applying a Computer Algebra System, specifically Mathematica animating the process. The program is robust allowing selecting 1) the spin value ω, 2) the restitution factor e and 3) the number of the bounces. Additional auxiliary quantities such as the reflection angle, range and etc. are also quantified. All the graphs and quantified values reported here in our investigation are produced using Mathematica [1] software and its accompanied text [4] and guidelines explained in a recently published book [5] .