The Zigzag Progression of Melting and Triple Point Properties of n-Alkanes, n-Alcohols, n-Alkanoic Amines and n-Alkanoic Acids ()
1. Introduction
In pharmaceutical and food industries, the phenomenon of crystalline polymorphism of cocoa butter is well-known. It may exist in several different crystal morphologies [1] : as crystalline state α with melting point 54˚C, β' with melting point 64˚C and β with melting point 73˚C [1] . Different morphological crystallites in cocoa butter may coexist and the percentage of every fraction of crystals depends on parameters in prehistory of the cocoa butter, such as the storage time and temperature. For this reason, different samples of cocoa butter can exhibit difference in melting point. The same has been observed for n-alkanes, aliphatic saturated acids, aliphatic saturated alcohols, aliphatic saturated amines, and other saturated and non-saturated substances as well as cyclic and polycyclic substances. Because of this, it is possible to find in literature different values for melting points of the same substance. Often the values can be significantly different.
The melting point is a significant parameter in chemistry: it can easily reflect the purity of the substance. For long list of substances as: n-alkanes, n-alcohols, n-alkanoic acids, lipids and some other, different melting points, which often have significant differences, had been presented in literature for the same substance. In some of these observations, the crystalline polymorphism had been pointed out as a cause for the phenomenon, but in several cases the cause was not pointed out. The careful comparison of melting points in several homologous series supports the perception that general differences are not the operator errors and do not result from crystal morphology of samples, but have more meaningful basis.
Despite of these differences some general tendencies in pure substances can be observed, such as the “zigzag” effect: a periodic alteration of some thermophysical properties added to a general smoother change. Among these properties are melting and triple point temperatures, triple point vapor pressure, liquid internal energy and some other properties [2] . The melting point is a significant parameter in chemistry: it can easily reflect the purity of the substance. For long list of substances as: n-alkanes, n-alcohols, n-alkanoic acids, lipids and some other, different melting points, which often have significant differences, had been presented in literature for the same substance. In some of these observations, the crystalline polymorphism had been pointed out as a cause for the phenomenon, but in several cases the cause was not pointed out. The careful comparison of melting points in several homologous series supports the perception that general differences are not the operator errors and do not result from crystal morphology of samples, but have more meaningful basis. Already in 1877 Baeyer [3] described the alternation in melting points of saturated dibasic acids and in 1905 Biach Z. also described the same alternations between the odd and even members of homologous series in different substances. Tsakalotos [4] in 1907 and later Forcrand in 1921 [5] and Timmermans in 1965 [2] published similar observations. If in the samples of the same substance the crystalline polymorphism is excluded as the cause of melting temperature variations, the zigzag progression of melting and triple point temperatures in homologous series becomes evident and can be investigated more carefully.
Boese, R. et al. [6] in 1999 investigated by the single-crystal X-Ray analysis the melting point alternation in short-chain n-alkanes and they have shown that a less dense packing in solid state is observed in the odd-numbered n-alkanes compared to the even-numbered members, which consequently lowers melting temperature. This is due to the crystal structure of the hydrocarbons in the solid state. They explained it as the even-numbered n-alkanes in solid state have optimal intermolecular interactions at both ends, while the odd-numbered ones possess these only at one end. They could not observe the packing effect in the case of alcohols and in the amine chains.
In the paper, we present data and calculations for several homologous series, which with no debt demonstrate the zigzag progression of melting and triple point temperatures in homologous series as a general phenomenon. For better perception of this wonderful phenomenon the visual analytics is very helpful. By presentation of graphical images the zigzag phenomenon is clearly visualized and supports generation of possible hypotheses for this intriguing property of molecules in the homologous series.
The possible technical applications [7] of this phenomenon and its implication will be discussed elsewhere in future papers.
2. The n-Alkanes’ Thermophysical Properties Zigzag Oscillations
The visual analysis of diagrams, based on precise experimental data for n-alkanes, permits to analyze the zigzag oscillations of several thermophysical properties. For n-alkanes with the carbon atoms number NC in a molecule from 1 to 12 the zigzag irregularities of some properties near the triple point have been analyzed. The main source of data was the NIST (National Institute of Standards and Technology, USA [8] ) database [9] , except for n-undecane. For this fluid, the data have been taken from the Vargaftik’s Handbook [10] .
At the triple points of n-alkanes had been analyzed the carbon atoms molar density DC:
 .
.
Here Dliqtr is the molar density of a liquid n-alkane at its triple point. For the carbon atoms’ molar density DC in liquid n-alkanes at their triple points it is possible to see the zigzag oscillating dependence on the number NC of C atoms in a molecule, Figure 1.
Starting from the NC = 3, the carbon atoms density DC in liquid n-alkanes at their triple points for odd numbers NC is larger than the average value of the nearest even numbers. In liquid methane and ethane, the molar densities of
![]()
Figure 1. The zigzag oscillation of the carbon atoms molar density DC in liquid normal alkanes at their triple points on the C atoms number NC in a molecule.
carbon atoms fall due to a growing proportion of hydrogen atoms for small numbers NC of C atoms in a molecule.
The zigzag dependence of the carbon atoms molar density DC in liquid n-alkanes may be partly explained by the zigzag dependence of the triple point temperature for n-alkanes on the C atoms number NC in a molecule. Linus Pauling in his book General Chemistry [11] presented the table of melting points for normal alkanes that shows the zigzag dependence on the C atoms number NC. It may be reflected in the triple point densities of liquid n-alkanes: the larger is the triple point temperature, the larger is the thermal expansion of a liquid.
Here the triple point temperature dependence on the number NC of C atoms in a molecule had been studied utilizing the NIST database [9] data. For n-undecane the melting temperature from the Vargaftik’s Handbook was used [10] . In this case the difference between melting temperature and triple point temperature for a substance under investigation is not too high and these values can be considered as the same thermophysical property.
For the triple point temperature, we see also the zigzag dependence on NC, starting from NC = 3, Figure 2. In methane and ethane, the triple point temperature grows due to a growing proportion of hydrogen-carbon bonds for small NC.
The oscillations of the Ttr(NC) are better seen from the second differential ∆2Ttr(NC):
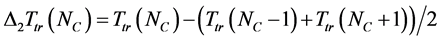 .
.
Roberts and Caserio [12] used the first differential to illustrate the zigzag dependence of the melting temperature in n-alkanes, but we think that the second differential demonstrates better the deviation of triple point temperatures in n-alkanes from their regular dependence.
Sedunov in 2012 has shown that n-alkanes’ molecules in gaseous dimers are packed in a parallel structure, which bond energy grows almost linearly with the number of carbon atoms, but with zigzag deviations from a straight line [13] . The longer is the n-alkanes’ molecule, the more C-H bonds is formed in a dimer. These bonds are not as strong as the chemical C-H bonds, but are much stronger
![]()
Figure 2. The dependences of the triple point temperature (blue rhombs) and critical temperature (red circles) for normal alkanes on the C atoms number NC in a molecule.
than ordinary van der Waals bonds. This enforcement of bonds may result from no zero charges of carbon and hydrogen atoms in n-alkanes.
In liquids, the intermolecular bond energy depends on the packing character. It is not surprising that the intermolecular bonding in liquid n-alkanes is like the bonding in the gas phase.
The Figure 3 demonstrates large oscillation values of the triple point temperature Ttr(NC) in a series of n-alkanes. The triple point temperature reflects the bond energies between molecules in the solid and liquid states.
The saturation vapor pressure is very sensitive to the bond energy between molecules in a liquid state. For the triple point vapor pressure Ptr the zigzag character of the Ptr(NC) dependence in a series of n-alkanes is clearly seen from the Figure 4. It is possible to see that the Ptr(NC) oscillations are very high and reach several orders of magnitude. Only methane deviates from the zigzag Ptr(NC) dependence.
All analyzed properties of n-alkanes at their triple points are reflected in the Table 1.
3. A Comparison of n-Alkanoic Acids’ and n-Alkanes’ Melting Temperatures
The n-alkanoic acids molecule contains the −COOH head part followed by the
![]()
Figure 3. The Ttr(NC) deviation from the nearest average value (Ttr(NC − 1) + Ttr(NC + 1))/2, demonstrating a high amplitude of Ttr oscillations in a series of normal alkanes.
![]()
Figure 4. The zigzag dependence of the triple point vapor pressure Ptr for normal alkanes on the C atoms number NC in a molecule.
![]()
Table 1. The thermophysical properties of n-alkanes at their triple points.
−Cn−1H2n−1 alkyl tail moiety, where n is the number of carbon atoms in the molecule, designated above as NC for n-alkanes. We can present an n-alkanes molecule also as the −CH3 head part, followed by the −Cn−1H2n−1 alkyl tail moiety. At the same number NC of carbon atoms, the alkyl tail of the n-alkanoic acid molecule is the same as the tail of the n-alkanes molecule. Basing on the group contribution principle [14] , we can wait a correlation in some thermophysical properties of n-alkanoic acids and n-alkanes.
Among other thermophysical properties the melting point has proven to be very sensitive to the liquid’s molecular structure. If we compare melting points in a series of n-alkanoic acids with the same of n-alkanes, we can see a similarity caused by the same alkyl tails and difference resulting from different head parts. The data are shown at the Table 2.
Calculating differences between melting temperatures of n-alkanoic acids and triple point temperatures of n-alkanes we ignore the difference between melting temperature and triple point temperature of a fluid under investigation, as a very small value.
The Figure 5 shows melting temperatures for n-alkanoic acids and triple point temperatures for n-alkanes in dependence on NC from 1 to 12.
We see that zigzag oscillations of two curves are similar. It tells about almost the same contribution of the Cn−1H2n−1 tails of n-alkanoic acids’ and n-alkanes’ molecules in the intermolecular bond energy. But there is a strong difference in the regular dependence, growing at small NC due to a growing role of the molecular head parts in the intermolecular bonding. To analyze this regular part, the plot of difference ∆Ttr between two curves versus NC is presented at the Figure 6.
We see that oscillations have disappeared, but at NC = 5 there is a strong change of the tangent of slope, signaling about a change in a molecular packing character in liquid n-alkanoic acids. So, the utilization of n-alkanes as reference liquids permits to reveal the transition in the packing mechanism of molecules in liquid n-alkanoic acids at NC = 5!
![]()
Table 2. The melting temperatures of n-alkanoic acids and triple point temperatures of n-alkanes and their differences for NC from 1 to 12.
![]()
Figure 5. Melting temperatures for n-alkanoic acids (blue rhombs, see Table 2) and triple point temperatures for n-alkanes (red circles) in dependence on the number NC of carbon atoms in a molecule.
![]()
Figure 6. The difference between melting temperatures for n- alkanoic acids and triple point temperatures for n-alkanes versus the number NC of carbon atoms in a molecule.
We explain this transition as the competition of attractions between −COOH head parts and n-alkyl tails. The pair of −COOH head parts of two n-alkanoic acids may form a cluster complex like the methanoic acid dimer, Figure 7.
In n-alkanoic acid dimers with NC > 1 the outstanding Hydrogen atoms are substituted by the n-alkyl −Cn−1H2n−1 tails. At NC > 5 the attraction energy between long n-alkyl tails becomes competitive with the hydrogen bonds energy of the head parts. In the liquid n-alkanoic acids at NC > 5 becomes essential the attraction of two parallel molecules, bound by their alkyl tails’ attraction forces.
4. A Comparison of n-Alcohols’ and n-Alkanes’ Melting Temperatures
For this comparison, the melting temperatures of n-alcohols have been measured in Norwegian Drug Control and Drug Discovery Institute (NDCDDI), because the data from different sources [15] [16] [17] differ significantly. The n-alcohol molecule contains −CH2OH head part followed by the −Cn−1H2n−1 n-alkyl tail moiety. The head part is strongly polar and forms two hydrogen bonds in the methanol dimer, Figure 8.
At NC > 1 the hydrogen atoms, opposite to the −C-O bond, are substituted by the −Cn−1H2n−1 n-alkyl moieties. The experimental data for melting temperatures demonstrate an essential contribution of the −Cn−1H2n−1 n-alkyl moieties. A comparison of n-alcohols’ and n-alkanes’ melting temperatures was performed by the analysis of second differentials
![]()
dependence on the number of carbon atoms in a molecule NC, Figure 9.
Unlike n-alkanoic acids, the second differential of the melting point ∆2 Tmeltn
![]()
Figure 7. The methanoic acid dimer bound by two hydrogen bonds (dotted lines).
![]()
Figure 8. A possible structure of the methanol dimer bound by two hydrogen bonds (dotted lines).
![]()
Figure 9. The second differentials of the melting point ∆2Tmeltn versus the number NC of carbon atoms in a molecule for n-alcohols (blue rhombs) and n-alkanes (red circles).
in n-alcohols is smaller than for n-alkanes and falls much quicker at large NC. It is reflected in the difference of melting temperatures for n-alcohols and n-al- kanes, Figure 10.
Comparing the Figure 6 and Figure 10 we see that the abrupt change of the Tmelt(NC) tangent of slope in n-alcohols is also present, but the values of Tmelt(NC) in n-alcohols are much smaller than in n-alkanoic acids. It tells that hydrogen bonds in n-alcohols are weaker than in n-alkanoic acids. It may result from the double bond −C=O in n-alkanoic acids raising the oxygen atoms’ charges as compared to their charges at an ordinary −C-O bond. In this case, as in the case of n-alkanoic acids, the tangent of slope change may result from the competition of polar molecular heads’ parts interaction with the n-alkyl tails’ moiety interaction.
At NC < 5 may dominate the polar interaction with opposite orientation of interacting molecules, shown at the Figure 8, but at NC > 4 may dominate the parallel structure of interacting molecules. A large interaction of n-alkanes’ tails may result from no zero charges of their carbon and hydrogen atoms.
The zigzag oscillations of the Tmelt(NC) in n-alcohols demonstrate a strong contribution of the n-alkyl tails in the bond energy of molecules in a liquid state. These oscillations are also clearly seen for numbers NC of carbon atoms in a molecule larger than 12, Figure 11, based on experimental data of NDCDDI. But here we meet a new phenomenon―the change of the oscillation phase, clearly seen at the Figure 11.
The Figure 11 demonstrates a strange phenomenon: the change of phase at NC = 16. The data of Mudge S. M. [15] [16] also show the change of phase, but at NC = 19. At NC > 20 the phase of oscillations is opposite to the phase at NC < 18, Figure 12.
A deeper analysis of this phenomenon in future may help to discover the physical mechanism of the melting temperature Tmelt(NC) oscillation. It may result from the charge of carbon atoms in n-alkanes’, n-alcohols’ and n-alkanoic acids’ molecules dependence on the number NC. The oscillating bond energy strength between parallel n-alkanes molecules or n-alkyl tails tells that the charge of carbon atoms depends on condition, is the number NC even or odd.
![]()
Figure 10. The difference between melting temperatures for n-alcohols and triple point temperatures for n-alkanes versus the number NC of Carbon atoms in a molecule.
![]()
Figure 11. The zigzag oscillations of the melting temperature Tmelt(NC) in n-alcohols, based on the data of NDCDDI, demonstrating change of phase at NC = 16.
![]()
Figure 12. The zigzag oscillations of the melting temperature Tmelt(NC) in n-alcohols demonstrating change of phase at NC = 19 according to data from [14] [15] .
5. The Zigzag Effect for n-Amines
In this section the amines with normal alkyl tails are considered. They contain the ammonia part with one hydrogen atom substituted by normal alkyl tail moiety. The data collected from the NIST database [17] and publications of Timmermans [18] and Richet [19] are presented in the Table 3.
The investigation of the melting Tm and boiling Tb temperatures dependences
![]()
Table 3. Some physics-chemical properties of n-amines.
*From [17] . ** From [19] .
on the C atoms number NC for n-amines reveals again the zigzag oscillation progression for Tm, Figure 13. But the Tb(NC) dependence does not demonstrate the zigzag behavior.
The comparison of melting points progress with NC for n-amines and n-al- kanes and the difference between these temperatures ΔTm(Nc) are shown at the Figure 14.
The Figure 14 shows that the interactions contribution of the −NH2 head parts smoothly falls with NC. The kink of ΔTm(Nc) at NC = 5 is not as sharp as for n-acids and n-alcohols. A smooth character of the ΔTm(Nc) tells that the contribution of n-alkyl tails in attraction of molecules is almost the same for n-amines and n-alkanes.
6. Discussion
6.1. The Tangent of Slope Change of the Melting Temperature Progression
The investigation of ΔTm(Nc) for n-alkanoic acids’, n-alcohols’ and n-alkanoic amines’ melting temperatures differences from the same for n-alkanes reveals the contribution of the head parts of molecules in the molecular interaction in a liquid state. The method to use the n-alkanes’ properties as reference values to study the tangent of slope change in homologous series of n-alkanoic acids, n-alcohols and n-alkanoic amines had not been described before. It may be used to study molecular interactions in other homologous series, including aliphatic substances with cyclic moieties.
The tangent of slope change for n-alkanoic acids’, n-alcohols’ and n-alkanoic amines' melting temperatures differences from the same for n-alkanes at Nc = 5 also has not been described before. The further investigation of this intriguing
![]()
Figure 13. Melting Tm (blue rhombs) and boiling Tb (red circles) temperatures dependences on the C atoms number NC for n-amines.
![]()
Figure 14. Freezing (melting) point temperatures of n-amines (blue rhombs), n-alkanes (red circles) and their difference (green triangles) in dependence on the carbon atoms number NC in a chain.
phenomenon should be proceeded to understand better the competition between the head parts and the n-alkyl tails’ moieties attractions in a liquid state of these substances.
6.2. Harmonic “Zigzag” Progression of Melting Temperatures in n-Alkanoic Acids
The phase shift of the zigzag oscillations for n-alkanoic acids’ melting temperatures at large NC numbers of carbon atoms in a molecule has not been described before. It tells about no van der Waals interaction between the n-alkyl tails of molecules in these substances. The further investigation of this intriguing phenomenon should be proceeded for other aliphatic substances.
6.3. The Contribution of the Carbon and Hydrogen Atoms’ No Zero Charges in n-Alkyl Tails’ Interactions
The hypothesis about no zero charges of carbon and hydrogen atoms in n-alkyl tails has not been formulated before. It may be confirmed by a comparison of the n-alkyl fluids’ and classical van der Waals Noble gases’ critical point temperatures at the same number Z of electrons in a molecule, Table 4. The critical
![]()
Table 4. The critical temperature for n-alkyl fluids and noble gases.
point temperature reflects the molecular interaction strength and grows with the number of electrons in a molecule of a van der Waals fluid.
The Table 4 shows that at the same number of electrons in a molecule the critical temperature in n-alkyl fluids is much over the same for corresponding Noble gases.
The difference between critical temperatures of n-alkyl fluids and corresponding Noble gases is impressive! It tells about no van der Waals molecular interactions in n-alkyl fluids, which may be explained by no zero charges of carbon and hydrogen atoms in their molecules.
A symmetric structure of n-alkyl molecules results in zero value for the dipole moment, but higher order moments may have no zero values, providing enlarged molecular attraction as compared to classical van der Waals fluids! The zigzag dependence of the melting temperatures on the number NC of carbon atoms in n-alkyl tail may result from the carbon atoms charge dependence on NC. This intriguing phenomenon, including the phase change at large NC values, should be investigated in future research works more carefully.
7. Conclusions
1) A general character of thermophysical properties’ zigzag behavior for a wide number of organic substances: saturated alkanoic (fatty) acids, n-alcohols, n-amines and n-alkanes, tells about a universal attraction mechanism between their n-alkyl tails;
2) The change of phase of the Tm(Nc) dependence at large Nc numbers tells about no trivial character of this mechanism;
3) The competition of n-alkyl tails’ attractions with strong polar attractions of the molecular head parts in saturated alkanoic (fatty) acids, n-alcohols and n-amines tells about no zero charges of carbon and hydrogen atoms in the n-alkyl tails;
4) A sharp kink of the ΔTm(Nc) dependence in saturated alkanoic (fatty) acids and n-alcohols tells about structural changes in liquid saturated alkanoic (fatty) acids and n-alcohols at Nc = 5.