Influence of the PCM Layer Location on the Multilayer Wall Thermal Performance ()
1. Introduction
With the development of society, demand in thermal comfort of buildings is rising increasingly; the energy consumption is correspondingly increasing. [1] [2] . Now energy storage systems are essential for reducing the time or rate mismatch between energy supply and demand, thereby contributing to energy saving and environment friendly [3] . Thermal energy storage can be done through sensible heat and latent heat storage. However, compared with the sensible heat storage system, the phase change material (PCM) becomes popular because it can afford structures to improve thermal storage capabilities with minimal change to the existing building design. Therefore, PCM has been widely used in buildings from many aspects, firstly for passive solar heating, then solar thermal storage walls, impregnated concrete blocks and ceramic masonry, PCM-En hanced gypsum board and interior plaster, using wall cavity insulation for floors and ceiling systems, for roofs and attics and so on.
Mandilaras, et al. [4] built a two-story typical family house out-fitted with PCM walls. The results showed that the wall thermal mass was enhanced during later spring, early summer and autumn. The decrement factor was reduced by 30% - 40% and the time lag was increased by approximately 100 min. Zhang, et al. [5] analyzed indoor wall surface temperature response of brick wall filled with PCM under outdoor fluctuating air temperature. The results indicated that PCM applied in the brick walls was beneficial for thermal insulation, temperature hysteresis and thermal comfort. Meanwhile, increasing the filled amount of PCM could make the indoor wall surface temperature fluctuation be significantly smoothed.
However, most of studies have ignored the influence of phase-change temperature arrange of PCM. As is known, only when the phase change of PCM occurs can the latent thermal storage performance be played, so the reasonable phase- change temperature arrange of PCM is the most important factor. Based on the above analysis, this paper builds four wall models, of which one is a reference subject and other three are the walls integrated with the PCM layer in the different location, and according to the previous studies [6] [7] , the optimal phase- change temperature arranges of PCM are proposed for the multilayer walls. Finally, the influence of the PCM layer location is numerically simulated on the wall thermal performance which is based on the outer climate condition of Chengdu, China.
2. Mathematical Formulation
2.1. Description of the Physical Model
To research the optimal location of the PCM layer in the multilayer wall, four walls are built as shown in Figure 1. Where, Figure 1(a) shows a common multilayer wall of the 220 mm thickness without the PCM layer as a reference subject, while Figures 1(b)-(d) show the multilayer walls of the 240 mm thickness with the PCM layer located in the internal side, the middle and the external side, respectively. Moreover, Table 1 presents material thermal physical property of all layers.
2.2. Thermal Boundary Conditions
Convection thermal boundary conditions are adopted in inner and outer sides. In outer side, the air temperature and the solar radiation intensity in Chengdu
![]()
Figure 1. Four wall models (a) without the PCM layer; (b) with the PCM layer located in the internal side; (c) with the PCM layer located in the middle; (d) with the PCM layer located in the external side.
![]()
Table 1. Thermophysical properties of materials.
city are as shown in Figure 2, while air temperature employs the regression equation of indoor comfortable temperature proposed by Humphreys and Nicol [8] [9] , as following:
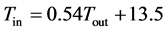 (1)
(1)
Considering the actual conditions of air-conditioning and heating, if the indoor air temperature from Equation (1) is greater than 25˚C in summer, indoor air temperature is set as 25˚C. Meanwhile, if the indoor air temperature from Equation (1) is less than 20˚C in winter, indoor air temperature is set as 20˚C. According to these, Figure 3 shows the variation of indoor air temperature in a typical year.
Considering the actual conditions of air-conditioning and heating, if the indoor air temperature from Equation (1) is greater than 25˚C in summer, indoor air temperature is set as 25˚C. Meanwhile, if the indoor air temperature from Equation (1) is less than 20˚C in winter, indoor air temperature is set as 20˚C. According to these, Figure 3 shows the variation of indoor air temperature in a typical year.
2.3. The Calculation Method Description of the PCM Phase Change Range
Only when the phase change of PCM occurs, the latent thermal storage performance can be played. And thus, the reasonable selection on the PCM phase-
![]()
Figure 2. Outdoor air temperature and the horizontal total radiation of Chengdu city in a typical year.
![]()
Figure 3. Indoor air temperature in a typical year.
change temperature arrange directly affects the PCM phase-change thermal storage performance effect. Therefore, this study refers to the calculation methods of the phase-change temperature range proposed by Meng, et al. [7] , as following:
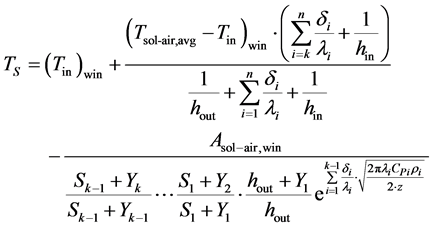 (2)
(2)
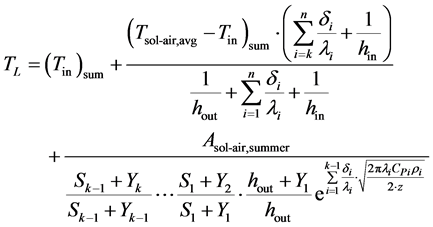 (3)
(3)
where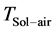 , avg and
, avg and 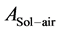 is the average vale and amplitude of outdoor comprehensive temperature, ˚C;
is the average vale and amplitude of outdoor comprehensive temperature, ˚C; 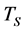 and
and 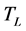 are solidus and liquidus temperatures ˚C;
are solidus and liquidus temperatures ˚C; 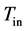 is indoor air temperature, ˚C;
is indoor air temperature, ˚C; 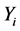 and
and 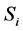 are the surface heat storage coefficient and the material heat storage coefficient of the
are the surface heat storage coefficient and the material heat storage coefficient of the 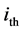 layer, W/(m2・K); hin and hout are inside and outside convective heat transfer coefficient, (W/(m∙K));
layer, W/(m2・K); hin and hout are inside and outside convective heat transfer coefficient, (W/(m∙K));  is the thermal conductivity of the
is the thermal conductivity of the 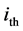 layer, W/(m2∙K);
layer, W/(m2∙K); 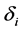 is the thickness of the
is the thickness of the ![]() layer,
layer,![]() ;
; ![]() is the specific heat of the
is the specific heat of the ![]() layer, J/(kg∙K);
layer, J/(kg∙K); ![]() is the density of the
is the density of the ![]() layer, kg/m3;
layer, kg/m3; ![]() is outdoor comprehensive temperature fluctuation period, 86,400 s; Subscripts “sum” and “win” indicate the hottest and the coolest parts of the PCM phase-change calculation period, respectively;
is outdoor comprehensive temperature fluctuation period, 86,400 s; Subscripts “sum” and “win” indicate the hottest and the coolest parts of the PCM phase-change calculation period, respectively;
Meanwhile, this study only consider the phase-change happening in summer and transition seasons. And PCM latent heat is 178.5 kJ/kg in this study. According to Equations (2)-(3), the theoretical values of PCM phase-change range under the different location of the PCM layer are shown in Table 2; on the basis of the thermophysical properties of wall materials in Table 1; outdoor and indoor thermal environment in Figure 2 and Figure 3 and wall structures in Figure 1.
2.4. Heat Transfer Model Description
Actually, the wall heat transfer is three-dimensional, but as the wall heat transfer occurs between inner and outer surfaces and thereby, there is only heat transfer along the wall thickness. Therefore, a three-dimensional problem can be approximately simplified to one-dimensional heat transfer along the wall thickness directions. Figure 4 shows a composite wall of N-layers showing boundary conditions and grid arrangement. Meanwhile, convection thermal boundary conditions are present on the both sides of ultrathin envelope. At the wall outer surface,
![]()
Table 2. Theoretical values of PCM phase-change range under the different location of the PCM layer.
![]()
Figure 4. Composite wall of N-layers showing boundary conditions and grid arrangement.
sol-air temperature includes the effect of outdoor air temperature combined with solar radiation. Air temperature at the wall inner surface represents indoor air temperature, which may be equal to the set temperature of air-conditioning.
Under the outer thermal environment variation with time, the heat transfer of the multilayer wall integrated with the PCM layer is the transient heat conduction with both melting and solidification of PCM. If a one-dimensional coordinate system is established with the coordinate origin at the thickness direction![]() , an enthalpy-porosity technique is utilized to simulate such dynamic heat transfer process [10] , and the governing equation is described as the following equation:
, an enthalpy-porosity technique is utilized to simulate such dynamic heat transfer process [10] , and the governing equation is described as the following equation:
![]() (4)
(4)
where T denotes the material temperature, ˚C; t is time, s; In the non-PCM layer, H can be shown as following:
![]() (5)
(5)
where ![]() expresses specific heat, J/(kg・K).
expresses specific heat, J/(kg・K).
In the PCM layer, H can be shown as following:
![]() (6)
(6)
where ![]() donates the latent heat of PCM, kJ/kg;
donates the latent heat of PCM, kJ/kg; ![]() is the liquid fraction and defined as following:
is the liquid fraction and defined as following:
![]() (7)
(7)
The convective heat transfer boundary conditions are adopted on the outer and inner surfaces (![]() and
and![]() ) and can be expressed as following:
) and can be expressed as following:
On the outer surface (![]() )
)
![]() (8)
(8)
On the inner surface (![]() )
)
![]() (9)
(9)
where ![]() and
and ![]() are inside and outside convectiveheattransfercoefficients;
are inside and outside convectiveheattransfercoefficients; ![]() and
and ![]() are indoor and outdoor air temperature, ˚C;
are indoor and outdoor air temperature, ˚C; ![]() and
and ![]() are outer and inner surface temperatures ˚C;
are outer and inner surface temperatures ˚C; ![]() is absorption coefficient, W/m2.
is absorption coefficient, W/m2.
2.5. Numerical Approach Description
The equations of the heat transfer model have been solved using the finite volume method in this simulation region. The finite volume formulation utilized in this algorithm ensures the energy conservation of wall heat transfer. A fully implicit scheme is applied for discretizing the time derivatives and a second-order central difference scheme is used for the diffusion terms. The corresponding algebraic equations are solved by the tri-diagonal matrix algorithm (TDMA). The convergence of the computations is declared at each time instant, when the following criterion is satisfied:
![]() (10)
(10)
where n is the internal iteration number.
2.6. Verification of the Wall Heat Transfer Model
To verify both accuracy and reliability of the unsteady calculation procedure on the enthalpy-porosity model, the research is done to numerically simulate the dynamic thermal response of the multilayer wall integrated with the PCM layer, which is researched experimentally by Kuznik and Virgone [10] and numerically by Zhang, et al. [11] . Figure 5 shows air temperature fluctuations and it compares the present results with published results. As shown in Figure 5, the present results agree well with the published results, especially with the simulation results of Zhang, et al. [11] , which demonstrate that the heat transfer model is effective and accurate, and also indicates that the predicted conclusions are verified by means of this mathematical model.
3. Results and Discussions
In order to study the influence of the PCM layer location on the wall thermal performance, indoor air temperature is designed as in Figure 3 and outdoor air temperature and the solar radiation intensity are as shown in Figure 2. In addition, the outside and inside convective heat transfer coefficients are 19 W/ (m2・K) and 8.7 W/ (m2・K) respectively [12] , and the solar radiation absorption coefficient is 0.6 for the outer surfaces. Meanwhile, the simulation has done for the heat transfer of walls integrated with the PCM layer, but inner surface transient temperature and heat flow are only showed in the periods of Aug. 1 - Aug. 7, which donates the summer condition, Apr. 1 - Apr. 7, which donates the transition season condition, and Jan. 1 - Jan. 7, which donates the winter condition.
![]()
Figure 5. (a) Variation of indoor and outdoor air temperature and (b) comparison of the present values with the experiment values and other numerical values.
3.1. The Optimal Verification of the PCM Phase Change Range Proposed in Equations (2)-(3)
Figure 6 shows variation of the surface temperatures for the PCM layer under the different locations of the PCM layer. As shown in Figure 6, for the different locations of the PCM layer, inner and outer surface temperatures of the PCM layer vary between liquidus and solidus temperatures basically, which shows the phase change always occur in the phase-change occurrence period and thereby that PCM has the good effects of the latent energy storage. Through the data processing, the covering rates of inner and outer surface temperatures are 98.4% and 97.3% for Wall 1 with the PCM layer located in the internal side, 98.4% and 97.3% for Wall 2 with the PCM layer located in the middle and 94.7% and 92.7% for Wall 3 with the PCM layer located in the external side, which shows the solidus and liquidus temperatures of PCM gained from Equations (2)-(3) can guarantee the PCM phase-change occurrence for the different locations of the PCM layer under the phase-change occurrence design period.
3.2. The Influence of the PCM Layer Location on Inner Surface Temperature
Figure 7 shows the transient variation of inner surface temperature under the different locations of the PCM layer. As shown in the figure, due to the integration of the PCM layer, the fluctuation amplitude is reduced for inner surface temperature and the temperature peak value is delayed with the different degrees, which shows PCM can refine the indoor thermal comfort. However, under the condition that the phase change of PCM occurs in summer and transition season, PCM can has the phase-change energy storage only in summer and transition season as shown in Figure 7(a) and Figure 7(b), and in winter, PCM
![]()
Figure 6. Variation of the surface temperatures for the PCM layer under the different location of the PCM layer (a)Wall 1, (b) Wall 2, (c) Wall 3.
temperature is less than the solidus temperature, and thereby, PCM is presented as the solid state. Therefore, in summer and transition season of Figure 7(a) and Figure 7(b), the reduced fluctuation amplitude is larger than that in the winter of Figure 7(c). On the other hand, the reduced fluctuation amplitude with the PCM layer located in the internal side is obviously larger than that with the PCM layer located in the middle, while the reduced fluctuation amplitude with the PCM layer located in the middle is obviously larger than that with the PCM layer located in the external side. Namely, when the PCM layer is closer to the wall internal side, the reduced fluctuation amplitude of inner surface temperature is larger and PCM has the larger improvement for wall thermal performance.
3.3. The Influence of the PCM Layer Location on Inner Surface Heat Flow
Figure 8 shows the transient variation of inner surface heat flow under the different locations of the PCM layer. As shown in the figure, due to the integration
![]()
Figure 7. Variation of inner surface temperature under the different locations of the PCM layer.
![]()
Figure 8. Variation of inner surface heat flow under the different locations of the PCM layer.
of the PCM layer, the fluctuation amplitude is reduced for inner surface heat flow and the peak heat flow value is delayed with the different degrees, which shows PCM can shift and reduce the peak air-conditioning load. However, due to the fact that PCM has not changed its phase in winter, the PCM layer location has not the influence on inner surface heat flow. On the other hand, in summer and transition season, when PCM can change its phase with outdoor thermal environment, the reduced fluctuation amplitude with the PCM layer located in the internal side is obviously larger than that with the PCM layer located in the middle and the external side. Namely, when the PCM layer is closer to the wall internal side, the reduced fluctuation amplitude of inner surface heat flow is larger.
Figure 9 shows the reduced percentage of the average heat flow values under the different locations of the PCM layer. As shown in the figure, due to the integration of the PCM layer, inner surface average heat flow is reduced obviously.
![]()
Figure 9. The reduced percentage of the average heat flow values under the different locations of the PCM layer.
Due to the fact that PCM can change its phase with outdoor thermal environment, their reduced percentage of the average heat flow values is larger than that in winter. On the other hand, when the PCM layer is closer to the wall internal side, the reduced percentage of inner surface heat flow is larger, and thereby, PCM has the higher energy saving efficiency.
4. Conclusions
In this study, the influence of the PCM layer location on the multilayer wall thermal performance is numerically researched under the climates conditions of Chengdu, China. However, influence of temperature and heat flow has been analyzed and the following conclusions can be drawn from the results obtained:
1) For three kinds of PCM layer, phase change is all occurred in summer and transition season. It has no effect in winter.
2) The application of PCM layer can reduce wall inner surface temperature and heat flow fluctuation, and the closer to inner surface, the more obviously this phenomenon is; which means the closer to wall inner surface, the better the effect of improving indoor comfort and wall thermal performance.
3) For three kinds of walls of different PCM layer location, wall 1 is the biggest energy saving wall, wall 2 is second and wall 3 is the last during summer and transition season, which means the best location of PCM layer is most close to inner surface when meeting other demand of wall structure.
4) Even though the walls are simplified ideal walls, the rule of temperature and heat flow is applicable for a real wall. So when making walls integrated PCM, PCM layer should laid close to wall inner surface as much as possible.
Acknowledgements
This research was supported and funded by MEXT, Japan (NO.142264)