Analysis on Characteristics of Precipitation Change from 1957 to 2015 in Weishan County ()
1. Introduction
With the rapid economic and social development, the study of climate change is very helpful to guide the industrial and agricultural production. In recent years, global climate change has attracted widespread attention; there are more and more people analyzing the current temperature, precipitation and other climate change [1] . Precipitation is the main source of surface fresh water. Only quite limited fresh water resource is available to human beings. Fresh water is particularly close to human beings that is a renewable resource because of processes such as precipitation and evaporation. The global average precipitation cycle is short, about 11 days. However, uneven distribution of annual and interannual precipitation in many areas often leads to the occurrence of drought and flood disasters. It is of great significance to explore the temporal and spatial variation of precipitation [2] . Large precipitation is closely related to national defense and socio-economic construction. Timely and appropriate precipitation can provide favorable conditions for the agricultural production, otherwise cannot [3] . Weishan County is located in the south of Dali Prefecture, with north subtropical monsoon climate, and the precipitation distribution is uneven in seasons, which can make use of limited water resource. Drought in winter, spring and early summer is serious. Rainy season starts late. Based on the linear regression analysis, cumulative anomaly method and Morlet wavelet method, the annual, seasonal and monthly precipitation characteristics of Weishan County are analyzed to reveal the regularity of multi-period-scale precipitation and climate abrupt change.
2. Data and Methods
2.1. Sources of Information
The annual precipitation, seasonal and monthly precipitation datum of Weishan County from 1957 to 2015 was calculated.
2.2. Research Methods
Four seasons are divided into: Spring to May, Summer to August, Autumn to November, Winter to February the following year [4] . The change of interdecadal precipitation was studied by using the mean method for 10 years. Regression analysis was performed using a linear fitting method [5] . Cumulative anomaly method is used to analyze the year of abrupt change of annual precipitation and calculate the signal-to-noise ratio [6] of the transition year to test whether the transition year has reached the standard of abrupt climate change. Morlet wavelet analysis method [7] [8] was used to analyze the precipitation cycle variation over the past 59 years.
3. Results and Analysis
3.1. Analysis of Interdecadal Variation of Precipitation
As can be seen from Table 1, the inter-decadal mean precipitation decreased from the 1990s to the 2010s. The inter-decadal average precipitation is the largest in the 1990s and the smallest in the 2010s.
3.2. Analysis of Interannual Variability of Precipitation
The linear regression analysis of the annual precipitation from 1957 to 2015 shows that the annual precipitation changes with the year number (Figure 1).
![]()
Table 1. 1957-2015 Weishan County inter-decadal average precipitation (mm).
![]()
Figure 1. Annual precipitation in Weishan County from 1957 to 2015 (mm).
We define a as one year. Wavy solid line for the annual precipitation, straight solid line for the average annual precipitation, dashed line for a linear regression line fitting trend line.
The annual precipitation change tends to decrease. The trend of annual precipitation is linearly −13.0 mm/10a. The average precipitation from 1957 to 2015 was 794.4 mm. The precipitation in 1973 is the largest precipitation in history. The precipitation in 1960 is the smallest precipitation in history. The correlation coefficient between annual precipitation and annual year number is 0.15 during 1957-2015, and F-test is not adopted. The result shows that the annual precipitation is not significant with the decrease of the year number.
3.3. Seasonal Variation of Precipitation
Based on the linear regression analysis and correlation analysis of the monthly precipitation from 1957 to 2015, the mean value, linear trend and correlation coefficient of seasonal precipitation were obtained in Table 2. F-test Two-sam- ple ANOVA was conducted to determine whether the significance of P and the yearly ordinal number of groups P reached significance level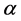 ,
, 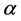 = 0.05, to test the reliability of correlation coefficient. The unit of precipitation in mm. The unit of linear propensity is mm/a.r is the correlation coefficient. * indicates the significance of 0.05 through the F-test.
= 0.05, to test the reliability of correlation coefficient. The unit of precipitation in mm. The unit of linear propensity is mm/a.r is the correlation coefficient. * indicates the significance of 0.05 through the F-test.
In winter, summer and autumn, the linear trend of precipitation is negative, which indicates that the precipitation in winter, summer and autumn decreases with the number of years, and the decreasing trend of precipitation is summer > autumn > winter. The correlation coefficient of precipitation in summer, autumn and winter did not pass the F-test with significance level of 0.05, which showed that the precipitation in summer, autumn and winter was not significant with the decrease of year number. The spring linear trend is positive, indicating that the spring precipitation increases with the year number. The correlation coefficient between the spring precipitation and the year serial number does not pass the F-test with the significance level of 0.05, indicating that the precipitation in spring is not significant with the increase of the year serial number.
3.4. Monthly Variation of Precipitation
The Average Monthly Precipitation, Linear Tendency of Monthly Precipitation, Correlation Coefficient of Monthly Precipitation were showed in Table 3. The linear trend of the monthly precipitation was negative in February, June, July, August, October, November and December, indicating that their monthly precipitation decreased with the year number. The correlation coefficient between precipitation and annual ordinal number in February and December has passed the F-test with the significance level of 0.05, which shows that the precipitation decreases with the year number in February and December is significant. In June, July, August, In October and November, the precipitation decreased with the year number was not significant. January, March, April, May and September were positive, indicating that their monthly precipitation increased with the year number. The correlation coefficient between January and April has passed the F-test with the significance level of 0.05, which shows that the precipitation in April is significantly increased with the year number. The precipitation in March, May and September is not significant with the year number. The increase of precipitation in January affects crop chilling injury. The increase of precipitation in March affects spring plowing. The increase of precipitation in April is good for agricultural production. The increase of precipitation in May affect the beginning of the rainy season ahead of the spring crop. The increase of precipitation in September affects a longer rainy season in autumn.
![]()
Table 2. Weishan County average precipitation, linear tendency, correlation coefficient.
![]()
Table 3. The average monthly precipitation, linear tendency, correlation coefficient.
3.5. Analysis of Abrupt Change in Precipitation
Morlet wavelet analysis was used to analyze the periodicity of annual precipitation from 1957 to 2015. The results shows that there is a long period of annual precipitation variation and short period of long period, indicating that the climate change of annual precipitation is formed by the superposition of different periods of shock. The phenomenon of abrupt climate change has became an important topic in climate change research. Climate change is a kind of discontinuity phenomenon in climate change process. Common climate factors accumulate anomaly curve to determine it.
Equation (1) is
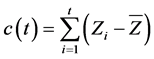
If the absolute value of the indicator reaches the maximum, the corresponding year is the mutation year. In order to test whether the transition to climate abrupt change criteria, then calculate the SNR in corresponding transition year.
Equation (2) is
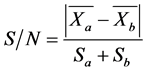
 and
and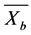 ,
, 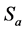 and
and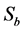 , respectively, for the transition year before and after the two stages of the average and standard deviation of the elements, the provisions of
, respectively, for the transition year before and after the two stages of the average and standard deviation of the elements, the provisions of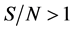 , the element can be considered in this year there is climate mutation, or mutation is not significant.
, the element can be considered in this year there is climate mutation, or mutation is not significant.
Figure 2 shows the cumulative precipitation anomaly curve. The precipitation anomaly datum from 1957 to 2015 is substituted into Equation (1) according to the method described above. The cumulative anomaly values are calculated and the cumulative precipitation anomaly curve (Figure 2) from 1957 to 2015 are plotted. As can be seen from Figure 2, the cumulative annual precipitation anomalies appear in 1969, 1974, 2003 and 2009, and these four transitional years are annual precipitation turning from partial to partial. In order to test whether the above-mentioned transition year has reached the standard of abrupt climate change, according to formula Equation (2), calculate the signal-to-noise ratio corresponding to the year of transition, and take 10 years of study before and after the transition year, we found that the corresponding SNRs of precipitation in 1969, 1974, 2003 and 2009 were 0.17, 0.33, 0.68 and 0.98. So the abrupt climate change was not significant and could only be used as the climatic transition year.
3.6. Periodicity Analysis of Precipitation
Figure 3 shows the time-frequency distribution of the square of the Morlet wavelet transform. We found that the signal intensity is different at different period scales. The strongest period-scale signals occurred in the period of 2 - 6 years, mainly occurred in 1965-1980; the period scale signal of 5 - 10 years was strong, mainly occurred in 1980-2015; 25 - 30a, 32 - 38a, 39a - 44a. The intensity of the signal on the period scale of 50a is weaker, and it is distributed over the whole period scale from 1957 to 2015.
Figure 4 shows the time-frequency distribution of the real part of Morlet wavelet transform, which indicates that the annual precipitation change has two aspects: the signal intensity and the phase, and the annual precipitation change is multi-period scale structure. As can be seen from Figure 4, the time-frequency distribution of the real part of Morlet wavelet transform is significant at the period scale of 2 - 10, 18 - 23, 25 - 32, and weak on the period scale of 45 - 54 years. The time-frequency changes of the real part of the wavelet appear as positive and negative phases alternatively, and the denser time scales are 8, 18 and 32.
Wavelet variance with periodic scale change process, known as wavelet variance. Figure 5 can reflect the annual precipitation in the period series contains a variety of scales (Cycle) fluctuations and its strength (Energy intensity) with the period scale of the characteristics of change. Each peak corresponds to a significant period. Therefore, it is possible to determine the main period scale (The main period) existing in a period series by the wavelet variance. As can seen from Figure 5, the peak of wavelet variance appears in the period scale a = 4, 8, 18, 32, the peak is the wavelet a variance of scale a. The period scale of 8, 32 of the oscillation is more intense.
![]()
Figure 2. The cumulative anomaly curve of annual precipitation from 1957 to 2015 (mm).
![]()
Figure 3. Time-frequency transformation of modulus square of wavelet transform.
As can be seen from Figure 6 that the real part of 8a-scale wavelet transform changes periodically with the year number. 1983 to 2015 amplitude than 1957 to 1982 large. The results show that the real part of the wavelet transform is the positive peak. The real part of the wavelet transform is an increasing function in the first four years, and the real part of the wavelet transform in the last four
![]()
Figure 4. The time-frequency distribution of wavelet real part.
![]()
Figure 6. The process of 8a-period scale wavelet transform.
years is a decreasing function. The real part of the wavelet transform is the negative peak. The real part of the wavelet transform corresponding to the first four years of the year is a decreasing function, and the real part of the wavelet transform is an increasing function in the last four years.
As can be seen from Figure 7, the real part of the 30a-scale wavelet transform varies periodically with the year number.1957-1990 is the first cycle, 1990-2015 is the second cycle. We found that, in the ideal case, the real part of the wavelet transform from 1957 to 1965, 1981 to 1997 and 2013 to 2015 increases with the number of years, ignoring the point where the real part of the wavelet transform is irregular. From 1966 to 1980 and 1998 to 2012, the real part of wavelet transform decreases with the number of years. The large period of 1957 to 1990 of Figure 7 is superimposed by four small periods of 1957 to 1990 in Figure 6, and the large period of 1990 to 2015 is superimposed by four small cycles of 1990 to 2015 in Figure 6. Indicating that there is an overlap of large and small periods of annual precipitation, and a small period exists in large cycle. The above-men- tioned rule can be used for medium and long-term climate prediction.
4. Conclusions
Based on the above analysis, the following conclusions can be drawn:
1) The trend of annual precipitation is −13.0 mm/10a in 1957-2015, and the annual precipitation is not significant. The precipitation of the four seasons is not significant with the decrease of the year number. The precipitation of winter, summer and autumn decreased with the year number, and the relationship between them was summer > autumn > winter. The spring precipitation increases with the year number.
2) In February, June, July, August, October, November and December precipitation decreased with the number of years. Precipitation decreased with the year number in February and December, but the precipitation in June, July, August, October and November did not significantly decrease with the year. The precipitation in January, March, April, May and September increased with the year number. The precipitation in April, April, May, September and September was not significant.
![]()
Figure 7. The process of 32a-period scale wavelet transform.
3) The cumulative annual precipitation anomaly peak appeared in 1969, 1974, 2003 and 2009; they did not pass the test of the signal to noise ratio test. It is considered that these years are to be the turning points of the annual precipitation. Before the turning year, the annual precipitation was large. After the turning year, the annual precipitation was small.
4) The annual precipitation is strong at the time scale of 2 - 6 years, mainly occurring in 1965-1980; 5 - 10 years period scale signal is strong, mainly occurring in 1980-2015; 25 - 30a, 32 - 38a, 39a - 44a, and 45 - 50a, were distributed over the whole period scale from 1957 to 2015.
5) There are obvious multi-scale periodic changes in the annual precipitation change, and its periodic variation is dominated by 8 years and 32 years.
6) At the periodicity of the real part of the 8a-scale wavelet, the real part of 1983-2015 is larger than that of 1957-1982. In the periodicity of the real part of the 32a-scale wavelet, 1957-1990 is for the first cycle, and 1990-2015 is for the second cycle.