Analysis of Ozone Behaviour in the City of Puebla-Mexico Using Non-Homogeneous Poisson Models with Multiple Change-Points ()
1. Introduction
It is a well known fact that air pollution may cause serious health problems to a susceptible population present in an environment affected by it. For instance, in [1] [2] [3] we have the study of the relation between exposure to ozone pollution and mortality in cities in the United States; [4] use regression models to study the effects of air pollution on lung development of children and adolescents. Finally, [5] use time series analysis to study the relation between ozone air pollution and mortality in Mexico City.
Given the oxidant nature of ozone, high levels of this pollutant may cause damage to the upper respiratory system. Therefore, a person already with some health problems may have its condition worsened. Thus, it is important to monitor the level of ozone and with that avoid population exposure to that pollutant. Hence, environmental authorities in several countries have implemented ozone standards and have used monitoring stations to keep track of ozone levels and see when the set standard is not obeyed. Using a continuous monitoring system, measures may be implemented in order to decrease ozone concentration and/or to alert the population of high levels.
During the past 30 years environmental authorities in Mexico and many of its cities have also implemented measures to monitor ozone concentration as well as alert the population of high levels of this and other pollutants. One of those measures is the construction of monitoring networks. Among the cities with some type of monitoring network is Puebla. Puebla is the capital of the state with the same name and has more than 5 million inhabitants with a car fleet of more than one million units. Puebla’s monitoring network was set in the year 2000 and has four stations, namely, Tecnológico (UTP), Ninfas (Nin), Serdán (Ser), and Agua Santa (AS). In addition to ozone other pollutants are also measured.
The interest here is in analysing the behaviour of the ozone data from the monitoring network of the city of Puebla in terms of estimating the probability of having an ozone environmental threshold exceeded a certain number of times in a time interval of interest. The study is performed using non-homogeneous Poisson models allowing the presence of change-points. Different rate functions are taken into account. They may depend on some parameters that need to be estimated. Estimation of the parameters involved is performed under the Bayesian point of view via Markov chain Monte Carlo algorithms.
This type of question has been posed and studied before, for instance, [6] as well as [7] where non-homogeneous Poisson processes without change-points are used to study the ozone behaviour in Mexico City. The latter work presents a Metropolis- Hastings algorithm to generate a sample of the parameters involved in the rate function of the non-homogeneous Poisson model. In [8] and [9] we have the use of non- homogeneous Poisson models allowing the presence of change-points also to study the ozone behaviour in Mexico City. Finally, [10] and [11] consider several rate functions for the non-homogeneous Poisson process. The former work compares their performances and in the latter, a Gibbs sampling algorithm programmed in R is given. The Gibbs algorithm is used to generate a sample of the parameters involved in the rate function of the Poisson process. Codes of some of the programmes used may be found in [7] , [8] , [11] and [12] . However, none of the works address the problem taking into account cities other than Mexico City, Mexico. Here, we consider ozone measurements obtained from the monitoring network of the city of Puebla, Mexico. Even though, the methodology used will also be non-homogeneous Poisson models allowing the presence of multiple change-points as in [9] and [10] , the data and the context are different from previous works. In addition to understanding the behaviour of ozone in Puebla, another aim is to compare the results obtained in the case of that city with the ones obtained in the case of Mexico City.
This paper is organised as follows. In Section 2, the several versions of the model considered here are described. Section 3 gives the Bayesian formulation of the models. In Section 4, an application to the case of ozone data from the city of Puebla, Mexico, is given. Finally, in Section 5, some comments are made.
2. The Non-Homogeneous Poisson Models
In order to use non-homogeneous Poisson models, let 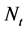 indicate the random variable recording the number of times that the environmental threshold of interest has been exceeded in the time interval
indicate the random variable recording the number of times that the environmental threshold of interest has been exceeded in the time interval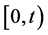 ,
,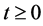 . We assume that
. We assume that 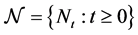 is a non- homogeneous Poisson process with rate and mean functions
is a non- homogeneous Poisson process with rate and mean functions 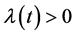 and
and
 , respectively,
, respectively,  , i.e., for
, i.e., for ,
,  ,
,
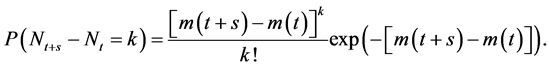 (1)
(1)
Let 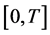 indicate the entire observational period and
indicate the entire observational period and 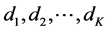 be the days in
be the days in  in which the environmental threshold of interest is exceeded. Hence,
in which the environmental threshold of interest is exceeded. Hence, 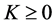 will denote the number of times that the threshold is exceeded in the time interval
will denote the number of times that the threshold is exceeded in the time interval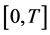 . The set
. The set 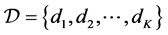 will indicate the set of observed data.
will indicate the set of observed data.
Several forms of rate functions are considered. We take some of the ones used in [10] . They are the Weibull (W), Musa-Okumoto (MO) [13] , Goel-Okumoto (GO) [14] , generalised Goel-Okumodo (GGO) and Webull-geometric (WG) [15] . They are given as follows,
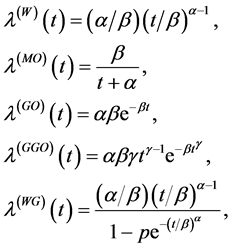 (2)
(2)
where 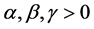 and
and![]() . The corresponding mean functions are ( [8] [9] [10] ),
. The corresponding mean functions are ( [8] [9] [10] ), ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and![]() .
.
When the presence of change-points is allowed, we have the following. Assume that there are ![]() of such points and let
of such points and let ![]() denote them. Therefore, the rate function of the non-homogeneous Poisson process has the following form ( [9] [10] )
denote them. Therefore, the rate function of the non-homogeneous Poisson process has the following form ( [9] [10] )
![]()
with ![]() one of the rate function given in (2). The corresponding mean function is ( [9] [16] )
one of the rate function given in (2). The corresponding mean function is ( [9] [16] )
![]()
where we take![]() , with
, with ![]() the mean function between the change-points
the mean function between the change-points ![]() and
and![]() ,
, ![]() , with
, with![]() ,
, ![]() the mean function before the first change-points and
the mean function before the first change-points and ![]() the mean function after the last change-point.
the mean function after the last change-point.
The vectors of parameters to be estimated are![]() ,
,
![]() , and
, and![]() , when no change-points are allowed. If
, when no change-points are allowed. If
![]() is the vector of possible change-points, then when they are allowed the vector of parameters to be estimated is
is the vector of possible change-points, then when they are allowed the vector of parameters to be estimated is![]() , where
, where ![]() is the vector of parameters of the corresponding rate function when
is the vector of parameters of the corresponding rate function when![]() ,
,
![]() , with
, with ![]() and
and ![]() the vectors of parameters in the case where
the vectors of parameters in the case where ![]() and
and![]() , respectively.
, respectively.
3. The Bayesian Setting
Estimation of the parameters will be performed using Bayesian inference ( [17] ). When we use Bayesian inference to estimate the parameters of a model, we assume that they are random quantities with some distribution assigned to them. Two distributions of interest are present, namely, the prior and posterior distributions. The former incorporates the researcher’s belief about the parameters behaviour before information about the data is incorporated. The latter takes into account that information, which is provided by the likelihood function of the model. Therefore, using the Bayesian approach, in addition to giving a point estimation of the parameters, a measure of uncertainty is also given when we consider the standard deviation and credible intervals for the estimates. Therefore, using the Bayesian point of view, we may describe the parameters in terms of their distributions and hence the information provided is more complete than just using a point estimation. Additionally, due to the complexity of the expressions for the likelihood functions of the models, the use of more classical methods may pose a problem.
Therefore, following in that direction, we use the existing relationship between prior and posterior distributions and the likelihood function of the model. The posterior distribution of a vector of parameters ![]() of a model describing a dataset
of a model describing a dataset ![]() is indi- cated by
is indi- cated by![]() . The posterior distribution is such that,
. The posterior distribution is such that, ![]() , where
, where ![]() and
and ![]() are the likelihood function of the model and the prior distribution of
are the likelihood function of the model and the prior distribution of![]() , respectively.
, respectively.
Since we are considering a non-homogeneous Poisson model, the general likelihood function when no change-points are present is given by ( [18] [19] )
![]() (3)
(3)
where ![]() and
and ![]() are the rate and mean functions, respectively, which will de- pend on the parameter
are the rate and mean functions, respectively, which will de- pend on the parameter![]() . In the case of presence of change-points we have that the likelihood function is ( [9] [16] )
. In the case of presence of change-points we have that the likelihood function is ( [9] [16] )
![]() (4)
(4)
where ![]() is the number of exceedances before the change-point
is the number of exceedances before the change-point![]() ,
,![]() .
.
The particular forms of the likelihood function, i.e., when we substitute the expression for the rate and mean functions in (3) and (4), are given in [9] , [10] , [11] . The forms of the prior distributions of the parameters as well as their hyperparameters are given when the models are applied to the data. Parameters are estimated using a Gibbs sampling algorithm ( [20] [21] ) internally implemented in the software OpenBugs (www.openbugs.net/w, [22] ). The codes are a straightforward modification of the pro- grammes presented in [12] and [23] .
Since many versions of the non-homogeneous Poisson model are considered, we need some criteria to select the model that best explains the behaviour of the data. Therefore, in addition to the graphical criterion, we also consider the deviance infor- mation criterion (DIC). The deviance is defined by![]() , where
, where ![]() is the vector of parameters of the model,
is the vector of parameters of the model, ![]() is the observed data,
is the observed data, ![]() is the likelihood function of the model, and c is a constant that is not needed when comparing the models. The DIC ( [24] ) is given by
is the likelihood function of the model, and c is a constant that is not needed when comparing the models. The DIC ( [24] ) is given by![]() , where
, where
![]() is the deviance evaluated at the posterior mean
is the deviance evaluated at the posterior mean![]() , and
, and
![]() is the effective number of parameters of the model. Smaller values of DIC indicate better models.
is the effective number of parameters of the model. Smaller values of DIC indicate better models.
Remark. Note that when we use the DIC we are contrasting the different models. The deviance takes into account the information provided by the likelihood function as well as the difference between the expected value of the deviance and its value when evaluated at the posterior mean of the vector of parameters. Therefore, we test one model against the other based on the information provided by the likelihood function of the model and taking into account how much the expected deviance differs from the one obtained using the estimated parameters.
4. An Application to Ozone Data from Puebla Monitoring Stations
In this section we apply the models described in previous sections to the ozone data obtained from the monitoring network of the city of Puebla, Mexico. The measure- ments correspond to the daily maximum ozone levels obtained from 01 January 2001 to 31 December 2009, giving a total of ![]() observed days. Measurements are made minute by minute and the averaged hourly results are reported in each of the four stations of the monitoring network. The daily maximum in a given station is the maximum of the 24 hourly averaged measurements. The daily maximum measurement for the city is the maximum among the daily maxima of all stations.
observed days. Measurements are made minute by minute and the averaged hourly results are reported in each of the four stations of the monitoring network. The daily maximum in a given station is the maximum of the 24 hourly averaged measurements. The daily maximum measurement for the city is the maximum among the daily maxima of all stations.
After obtaining the daily maximum measurements for stations UTP, Nin, Ser, and AS, there were 10%, 36%, 35%, and 21%, respectively, of data missing. Therefore, it was necessary to estimate the missing values. The methodology used was the following. If on the ith day of the jth year the measurement was missing, then if on that same day on the ![]() and
and ![]() years the data were available, we substitute the missing value by an average of the measurements present on that day on the
years the data were available, we substitute the missing value by an average of the measurements present on that day on the ![]() and
and ![]() years. If those values were also missing, then we would go back and move forth another year and do the same procedure. This method is not the best, but due to the nature of the data (similar behaviour for similar period in different years) the results were not that bad.
years. If those values were also missing, then we would go back and move forth another year and do the same procedure. This method is not the best, but due to the nature of the data (similar behaviour for similar period in different years) the results were not that bad.
Figure 1 shows the plots of the daily maximum ozone measurements for the city of Puebla during the observational period considered here where we have already imputed the missing data.
After completing the datasets and obtaining the daily maximum ozone measure- ments for the city, we have that during the observational period the mean measurements (in parts per million-ppm) was 0.065 with a standard deviation of 0.026. The environ- mental threshold considered here was 0.11 ppm (which was the Mexican environmental threshold during the time frame in which the measurements were taken [25] ). That threshold was exceeded ![]() times during the observational period.
times during the observational period.
We start by considering the case where no change-points are allowed and move to assume their presence as necessary. In all cases we assume prior independence of the parameters. Also, in all cases the estimation of the parameters was performed with a sample of size 10,000 using a sample gap of 10 collected after a burn-in period of 20,000.
![]()
Figure 1. Daily maximum ozone measurements (observed and estimated) for the period of 01 January 2000 to 31 December 2009.
Throughout this work we use U(a, b) to indicate the uniform distribution on the interval (a, b), and we use Gamma(c, d) to indicate the gamma distribution with mean c/d and variance c/d2.
We will report the estimated parameters only for the selected model. The inclusion of change-points will be performed in the cases where the graphical fit requires so.
4.1. Models with No Change-Points
When no change-points are considered, the likelihood function is given by (3). The prior distribution of the parameters in the case of no change-points are given in Table 1.
Remark. We would like to point out that, in a preliminary run of the algorithm, we have considered uniform prior distributions for all parameters, By doing that, we let the weight of information about their behaviour be dictated by the likelihood function of the model. After this preliminary run and after analysing the shape of the posterior distributions of the parameters, more informative prior distributions were assigned to them. The shapes suggested that either uniform or gamma distributions could be taken as prior distributions. We have also taken into account the fact that the parameters are all greater than zero. The hyperparameters used in the preliminary run were such that we had distributions with large variance. In the case of the final run, the hyperparameters were obtained based on the results of the preliminary run.
The values of DIC were 1249, 1288, and 1250 in the cases of W, MO, and WG rate functions, respectively. When considering the cases of the GO and GGO models, the value of the DIC was 1248. Therefore, the models with smallest DIC are models GO and GGO followed closely by the W and WG. The only model with a more distinctive value of DIC is the MO. Note that the DIC values for models W, GO, GGO, and WG differ by less than 10. Hence, from [26] , there is no conclusive evidence that they are significantly different. The only model that might be considered significantly different is the MO.
In Figure 2 we have the plots of the observed and estimated means using all rate functions considered here.
It is possible to see that even though the models using WG, W, GO, and GGO rate functions are the ones approaching better the observed mean, there is the need to include at least one change-point in the models. Hence, we start by assuming first the presence of just one change-point. By the information provided by the DIC, we have
![]()
Table 1. Prior distributions of the parameters of the models W, MO, GO, MO, GGO, and WG, when no change-points are present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
that the MO model is the only one that is significantly different from the others. Additionally, we may say that there is no significant difference among the remaining models. Therefore, due to its simplicity, we choose to continue with the Weibull rate function. Thus, we assume the presence of a change-point only in the W and MO models.
4.2. Models with One Change-Point
The vector of parameters in the present case is![]() . Their prior distributions are given in Table 2.
. Their prior distributions are given in Table 2.
The values of DIC for the W and MO models are 1226 and 1249, respectively. Hence, the chosen model would be the one assuming a Weibull rate function. Figure 3 gives the plots of the estimated and observed accumulated means when one change-point is
![]()
Figure 2. Observed (thinner continuous line) and estimated accumulated means when the models W (dashed line), MO (thicker dashed line), GO (thicker continuous line), GGO (dotted line), and WG (thinner dashed line) are considered and no change-points are allowed.
![]()
Table 2. Prior distributions of the parameters of the models W and MO when one change-point is present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
allowed and rate functions W and MO are used.
Looking at Figure 3 we may see that the model using the Weibull rate function provides better fit to the observed mean. However, we may also see that perhaps with the addition of more change-points the fit may improve for both the W and MO models.
4.3. Models with Two Change-Points
If we consider the presence of two change-points, then the vector of parameters to be estimated is ![]() with
with![]() ,
, ![]() , and
, and![]() . Their prior distributions are given in Table 3.
. Their prior distributions are given in Table 3.
The values of DIC for the W and MO models are 1220 and 1259, respectively. There- fore, based on the DIC values the chosen model would be the one assuming a Weibull rate function. Figure 4 gives the plots of the estimated and observed accumulated means
![]()
Figure 3. Observed (thinner continuous line) and estimated accumulated means when models W (dashed line) and MO (thicker continuous line) are considered and one change-points is allowed.
![]()
Table 3. Prior distributions of the parameters of the models W and MO when two change-points are present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
where two change-points are present and models W and MO are considered.
Looking at Figure 4 we may see that even though the W model provides a good fit, perhaps an additional change-point should be included. Also notice that even though towards the end and beginning of the observational period, the MO model provides a good fit, in the middle that is not good at all. Therefore, we have decided to continue with both models and include an additional change-point.
4.4. Models with Three Change-Points
In the models with three change-points, the vector of parameters to be estimated is ![]() with
with![]() ,
, ![]() , and
, and![]() . Table 4 gives
. Table 4 gives
![]()
Figure 4. Observed (thinner continuous line) and estimated accumulated means when models W (dashed line) and MO (thicker continuous line) are considered and two change-points are allowed.
![]()
Table 4. Prior distributions of the parameters of the models W and MO when three change- points are present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
the prior distributions of all parameters in the W and MO models.
The values of DIC for the W and MO models are 1225 and 1235, respectively. Therefore, we see that the chosen model would be the one assuming a Weibull rate function. However, the difference between the DIC obtained when using the W rate function differ from the one using the MO by a value of 10. Hence, ( [26] ) there is not a conclusive evidence that the W rate function with three change-points is better than the MO model with three change-points to explain the behavior of the data. Figure 5 gives the plots of the estimated and observed accumulated means in the case of three change-points and models W and MO.
Note that even though the MO model presents a good fit in the beginning of the observational period, we have that at the end of this period the W model fits better. We also have that the model assuming a Weibull rate function gives the best overall fit. However, it is clear that the inclusion of more change-points could be necessary.
4.5. Models with Four Change-Points
When four change-points are allowed, the vector of parameters to be estimated is
![]() with
with![]() ,
, ![]() , and
, and![]() . The prior distributions are given in Table 5.
. The prior distributions are given in Table 5.
The values of DIC for the W and MO models are 1199 and 1200, respectively. Hence, we may see that of the models with four change-points the one with smallest DIC is the
![]()
Figure 5. Observed (thinner continuous line) and estimated accumulated means when models W (dashed line) and MO (thicker continuous line) are considered and three change-points are allowed.
one assuming a Weibull rate function. However, we may also see that the model using the Musa-Okumoto rate function is not significantly different from the one using the Weibull rate function ( [26] ). Hence, both models could be considered to explain the behaviour of the data. Figure 6 gives the plots of the estimated and observed accumu- lated means when four change-points are allowed and the W and MO rate functions are considered.
Looking at Figure 6 we may see that with the inclusion of a fourth change-point the model MO adjusts better to the observed mean than when using the W model. Never- theless, we may see that perhaps a fifth change-point should be included in the models.
![]()
Table 5. Prior distributions of the parameters of the models W and MO when four change-points are present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
![]()
Figure 6. Observed (thinner continuous line) and estimated accumulated mean when models W (dashed line) and MO (thicker continuous line) are considered and four change-points are allowed.
4.6. Models with Five Change-Points
If we consider five change-points, then the vector of parameters to be estimated is
![]() with
with![]() ,
, ![]() , and
, and
![]() . The prior distributions are given in Table 6.
. The prior distributions are given in Table 6.
The values of DIC for the W and MO models are 1139 and 1148, respectively. Based on these values we may see that the smallest value corresponds to the W model. However, since the DIC for the MO model differs by less than 10, there is not a significant evidence that the W models is better than the MO. Figure 7 gives the plots
![]()
Table 6. Prior distributions of the parameters of the models W and MO when five change-points are present. The symbol “--” is used to indicate that a parameter is not part of a particular model.
![]()
Figure 7. Observed (thinner continuous line) and estimated accumulated means when models W (dashed line) and MO (thicker continuous line) are considered and five change-points are allowed.
of the estimated and observed accumulated means in the case of presence of five change-points and models W and MO.
Looking at Figure 7 we may see that the model assuming the Weibull rate function provides a good fit to the observed mean. However, the best overall fit is given by the MO model.
5. Discussion and Some Comments
In this work we have, initially, considered several rate functions for the non-homo- geneous Poisson process counting the number of times that the ozone environmental threshold 0.11 ppm was exceeded in a time interval of interest. Some rate functions considered previously in the literature ( [9] [10] [11] [12] ) to study the problem using ozone data from Mexico City are used to analyse the data from the monitoring network of the city of Puebla.
Models without the presence of change-points and allowing their presence are taken into account. The model that best explains the behaviour of the data is selected using a graphical criterion and the DIC. When using the DIC, the smallest value corresponds to the model using the Weibull rate function and allowing the presence of five change- points. However, when we look at the DIC in the case of the model using the Musa- Okumoto rate function with the presence of five change-points, we may notice that the value differ of that of the W model by less than 10. Therefore, there is not enough evidence to conclude that both models are significantly different ( [26] ). We may also see that the models with four change-points may also be considered not significantly different when we use the DIC to select the best model. In fact, that property is present from the case where three change-points are considered on.
Remark. Note that a preliminary analysis of the accumulated observed mean (i.e., the mean obtained directly from the data) shows the possible existence of change-points. In order to either confirm or discard their presence, several versions of the model were considered. The different results were compared using the DIC and the graphical fit. Hence, we have tested the different hypotheses about the model that would better explain the behaviour of the data. Also, note that the change-points were estimated as well as the parameters of the rate functions. We have assigned a prior distribution to them and using a sample drew from the respective posterior distribution we have estimated those change-points as well their credible intervals. Note that plots of the estimated means were drawn using the estimated parameters which were product of a sample from their posterior distributions. We would like to call attention to the fact that in addition to the plots of the accumulated observed and estimated means, a measure of the discrepancy between observed and estimated means were also used, namely the DIC.
If we use the graphical criterion to select the model that best explain the behaviour of the data, then when looking at Figures 2-7, we may see that the fit of the estimated accumulated mean to the observed one, improves as we let the number of change- points to increase. We may also see that the best graphical fit is provided by the model assuming the Musa-Okumoto rate function and allowing the presence of five change- points.
Therefore, taking into account the two model selection criteria considered here, there is an indication that the model that should be chosen to explain the behaviour of the ozone data from the city of Puebla is the one assuming the Musa-Okumoto rate function allowing the presence of five change-points. This result differs from the ones obtained in the case of Mexico City, where the Weibull model is the one that provides the best fit in almost all cases ( [6] [9] [10] [12] ). In spite of having the MO model as the one graphically fitting better the data, because of the values of the DIC, we have decided to present the estimated parameters for both the Weibull and Musa-Okumoto rate functions when we allow the presence of five change-points. Table 7 gives the estimated quantities of interest for the W and MO models.
We would also call attention to the fact that when we consider the Weibull rate function it presents a decreasing behaviour between the second and fourth change- points, and after the fifth (values of ![]() smaller than one). However, for the times before the second change-point, and between the fourth and fifth, the Weibull rate function presents an increasing behaviour. Therefore, for most of the observational period, the rate functions between change-points are decreasing functions.
smaller than one). However, for the times before the second change-point, and between the fourth and fifth, the Weibull rate function presents an increasing behaviour. Therefore, for most of the observational period, the rate functions between change-points are decreasing functions.
![]()
Table 7. Bayesian estimates of the parameters of the non-homogeneous Poisson model for the Weibull and Musa-Okumoto rate functions when five change-points are allowed.
Since the Musa-Okumoto model with five-change-points is the one whose graphical fit is the best and since by the DIC there is not a significant difference between the W and MO models with five change-points, from now on we consider only the latter.
Figure 8 shows the plots of the estimated Musa-Okumoto rate function in the time subintervals between change-points and also before and after the first and last change- points, respectively. It is possible to see that the plots are also of decreasing functions (as noted before in some time subintervals between change-points when the Weibull rate function is used) in each subinterval. However, it is possible to see that during the time subinterval between the fourth and fifth change-points the values of the rate function are larger than the values in the other subintervals with the exception of the time subinterval before the first and second change-points. The time subinterval between the fourth and fifth change-points corresponds to a period between the beginning of the year 2005 and the end of the year 2007. In spite of having a decreasing behaviour in the time interval between the fourth and fifth change-points it is possible to see that exceedances occur at a much higher rate than at neighbouring time subintervals.
In the same manner as in previous works ( [6] [9] [10] [12] ), we may use the estimated mean function which in the present case is the Musa-Okumoto, to calculate the probability (1) for different values of k and different time intervals.
Acknowledgements
We thank an anonymous reviewer for the comments and questions that helped us to
![]()
Figure 8. Estimate Musa-Okumoto rate function for the time subintervals between change-points.
improve the presentation of this work. ERR and JACJ received partial financial support from the projects PAPIIT-IN102713 and IN102416 of the Dirección General de Apoyo al Personal Académico of the Universidad Nacional Autónoma de México (UNAM), Mexico. JACJ thanks the Instituto de Matemáticas-UNAM, Mexico, for the hospitality and support received. This work is a consequence of JACJ’s Master’s Dissertation.