Torque Free Axi-Symmetric Gyros with Changing Moments of Inertia ()
1. Introduction
A gyro is a body of rotation which is set spinning at a large angular velocity around its axis of symmetry. The most important practical applications of gyros are met in devices for measuring the orientation or maintaining the stability of airplanes, spacecrafts and submarine vehicles in general. Various gyros are used as sensors in inertial guidance systems. Most textbooks in introductory mechanics explain the mysterious behavior of a spinning gyro by using Lagrange equations and severe mathematics [1] [2] . Other textbooks [3] [4] treat the problem of torque-induced precession of a top based on Euler equations, which are referred to the non-inertial reference frame rotating together with the body. The problem of the torque free inertial rotation of a symmetrical top is discussed, in particular, in [5] and illustrated by a simulation computer program (free rotation of an axially symmetrical body) [6] . For our problem, we consider a gyro body with xyz-coordinate system fixed of it, such that the z-axis of the body is the axis of symmetry and the inertia tensor is assumed to take the form
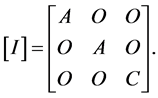 (1.1)
(1.1)
Here A and C are the principal moments of inertia in the x and z directions.
The rate of change of the inertia tensor with respect to time takes the form
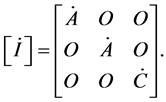 (1.2)
(1.2)
We note that the inertia products remain zeros.
Assume that the angular velocity of the satellite or the gyros is
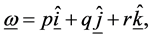 (1.3)
(1.3)
and the angular momentum is
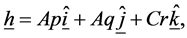 (1.4)
(1.4)
where 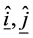 and
and 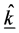 are the unit vectors in the
are the unit vectors in the 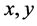 and
and 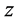 directions.
directions.
Thus the gyro’s kinetic energy of rotation becomes
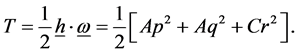 (1.5)
(1.5)
2. Equations of Motion
Applying Euler’s equations of motion and putting the applied torque equal zero, we get
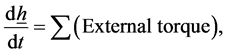 (2.1)
(2.1)
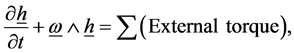 (2.2)
(2.2)
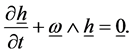 (2.3)
(2.3)
For the considered problem (mentioned above) we apply the angular momentum principle to get
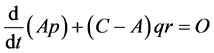 , (2.4a)
, (2.4a)
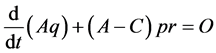 , (2.4b)
, (2.4b)
 . (2.4c)
. (2.4c)
3. Components of Angular Momentum
The Equation (2.4c) can be integrated to give
![]()
We can conclude that the z-component of the angular moment is constant, that is
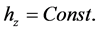 (3.1)
(3.1)
The angular velocity is obtained by multiplying the Equations (2.4a) by ![]() and (2.4b) by
and (2.4b) by ![]() and adding the resulted equations, we get
and adding the resulted equations, we get
![]() , (3.2)
, (3.2)
![]() (3.3)
(3.3)
that is ![]() or
or![]() (3.4)
(3.4)
where![]() .
.
Thus the![]() ―component of angular momentum is constant
―component of angular momentum is constant
![]() (3.5)
(3.5)
The ![]() and
and ![]() can be shown, see Figure 1.
can be shown, see Figure 1.
For torque free axi-symmetric gyro, angular velocity![]() , angular momentum
, angular momentum![]() ,
,
![]()
Figure 1. The angular momentum components.
and the gyro’s symmetry axis lie in one plane [7] .
Since the Equations (3.1) and (3.5) represent the angular momentum components, it can be deduced that the nutation angle remains constant when the inertia moments change as it when the inertia moments does not change.
For the components of angular velocity (3.4), we introduce the auxiliary frequency ![]() defined by
defined by
![]() , (3.6)
, (3.6)
then
![]() . (3.7)
. (3.7)
The two Equations (2.4a) and (2.4b) can be combined to yield
![]() . (3.8)
. (3.8)
The solution of this differential equation can be obtained as
![]() . (3.9)
. (3.9)
If the constant![]() , and in order to find the value of constant
, and in order to find the value of constant ![]() we employ the Equation (3.5) to get
we employ the Equation (3.5) to get ![]() and then
and then
![]() , (3.10)
, (3.10)
![]() , (3.11)
, (3.11)
![]() , (3.12)
, (3.12)
where![]() .
.
We can get the![]() ―component of the angular velocity at any instant by using
―component of the angular velocity at any instant by using
![]() (3.13)
(3.13)
![]() (3.14)
(3.14)
where the subscript (0) refers to values of time ![]()
The components of angular velocity can be shown, see Figure 2.
The angular velocity component ![]() has a relative angular velocity
has a relative angular velocity ![]() in the xy- plane.
in the xy- plane.
Introducing a floating ![]() coordinate system, we can express the angular velocity (
coordinate system, we can express the angular velocity (![]() ) by using the
) by using the ![]() or the
or the ![]() coordinate system.
coordinate system.
The Equations (3.11) and (3.12) show that the component ![]() and consequently v-axis and u-axis are perpendicular, such that u-axis rotates with a relative angular velocity
and consequently v-axis and u-axis are perpendicular, such that u-axis rotates with a relative angular velocity ![]() where
where
![]()
In the xy-plane, the z-component of the absolute angular velocity of v-axis is
![]()
Figure 2. The components of angular velocity.
![]() (3.15)
(3.15)
We can find that, for a flattened gyro![]() , the v-axis rotates faster than the x-axis, and for elongated gyro
, the v-axis rotates faster than the x-axis, and for elongated gyro ![]() the v-axis rotates more slowly than the x-axis.
the v-axis rotates more slowly than the x-axis.
Thus, the ![]() coordinate system moves with an angular velocity
coordinate system moves with an angular velocity
![]() (3.16)
(3.16)
The angular velocity ![]() of the gyro body and the angular velocity
of the gyro body and the angular velocity ![]() of the floating
of the floating ![]() coordinate system are related by
coordinate system are related by
![]() . (3.17)
. (3.17)
where ![]() is the spin of the gyro.
is the spin of the gyro.
4. Euler Frequencies
The frequency of the angular momentum remains constant since there is no external torque applied to the gyro [8] , the direction of the angular momentum vector may be used to define as space-fixed coordinate axis L which assigned to Z-axis and is called the precession axis [9] .
If the z-axis of the rotating ![]() coordinate system is the symmetry axis of the gyro, the v-axis lies in a plane formed by the Z- and z- axes, and we write
coordinate system is the symmetry axis of the gyro, the v-axis lies in a plane formed by the Z- and z- axes, and we write
![]() . (4.1)
. (4.1)
The nutation angle ![]() is the angle between the z-axis and Z-axis where Z-axis and L are coincide, see Figure 3.
is the angle between the z-axis and Z-axis where Z-axis and L are coincide, see Figure 3.
The components of ![]() for elongated axis symmetric gyro are obtained from the shape, so
for elongated axis symmetric gyro are obtained from the shape, so
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
The nutation angle remains a constant and the gyro is carry out a steady precession about the angular momentum vector, since
![]() (4.4) we obtain
(4.4) we obtain
![]() (4.5)
(4.5)
![]() . (4.6)
. (4.6)
Also from the figure
![]() (4.7)
(4.7)
Also for the angle ![]() between the z-axis and the angular velocity
between the z-axis and the angular velocity ![]() axis, we have
axis, we have
![]() . (4.8)
. (4.8)
The motion of a torque free gyro with rotational symmetry and changing moment of inertia can be visualized by imaging a space cone and body cone as shown see Figure 4 and Figure 5.
We can obtain the relation between the precession and the spin as follows
![]() . (4.9)
. (4.9)
For the elongated gyro ![]() we find that
we find that ![]() and
and ![]() and
and ![]() have the same sign then the precession is direct.
have the same sign then the precession is direct.
For the flattened gyro ![]() we find that
we find that ![]() and
and ![]() have the opposite signs, then the precession is retrograde.
have the opposite signs, then the precession is retrograde.
5. Conclusions
The system (2.4) is integrated to obtain the angular velocities and the angular momentum,
![]()
Figure 4. Space cone and body cone for an elongated gyro.
![]()
Figure 5. Space cone and body cone for a flattened gyro.
then Euler’s angles are deduced. The motions are classified into two cases:
1) the elongated gyro![]() .
.
2) the flattened gyro![]() .
.
For each case, we investigate the equations of motions, the precession, the nutation and the spin for these motions in detailed by using the analytical techniques and the illustrated shapes. The obtained results can be applied on the satellites [10] with rotational symmetry and changed inertia moments, the antennas [11] [12] and the solar power collector systems [13] .
Acknowledgements
This project is supported by Institute of Scientific Research and Islamic Heritage Revival, Umm Al-Qura University, Saudi Arabia.