Some Common Fixed Point Theorems for Four Mappings in Dislocated Metric Space ()
1. Introduction
In 1986, S. G. Matthews [1] introduced some concepts of metric domains in the context of domain theory. In 2000, P. Hitzler and A. K. Seda [2] introduced the concept of dislocated topology where the initiation of dislocated metric space is appeared. Since then, many authors have established fixed point theorems in dislocated metric space. In the literature, one can find many interesting recent articles in the field of dislocated metric space (see examples [3] - [12] ). Dislocated metric space plays very important role in topology, semantics of logical programming and in electronics engineering.
The purpose of this article is to establish some common fixed point theorems for two pairs of weakly compatible mappings with (E. A.) and (CLR) property in dislocated metric space.
2. Preliminaries
We start with the following definitions, lemmas and theorems.
Definition 1. [2] Let X be a non empty set and let 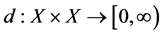 be a function satisfying the following conditions:
be a function satisfying the following conditions:
1) 
2) 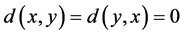 implies
implies 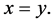
3) 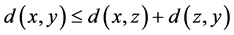 for all
for all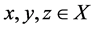 .
.
Then, d is called dislocated metric (or d-metric) on X and the pair (X, d) is called the dislocated metric space (or d-metric space).
Definition 2. [2] A sequence  in a d-metric space
in a d-metric space  is called a Cauchy sequence if for given
is called a Cauchy sequence if for given , there corresponds
, there corresponds  such that for all
such that for all , we have
, we have .
.
Definition 3. [2] A sequence in d-metric space converges with respect to d (or in d) if there exists 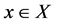 such that
such that  as
as 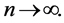
Definition 4. [2] A d-metric space 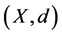 is called complete if every Cauchy se- quence in it is convergent with respect to d.
is called complete if every Cauchy se- quence in it is convergent with respect to d.
Lemma 1. [2] Limits in a d-metric space are unique.
Definition 5. Let A and S be two self mappings on a set X. If 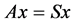 for some
for some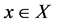 , then x is called coincidence point of A and S.
, then x is called coincidence point of A and S.
Definition 6. [13] Let A and S be mappings from a metric space ![]() into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is,
into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is, ![]() for some
for some ![]() implies
implies ![]()
Definition 7. [14] Let A and S be two self mappings defined on a metric space![]() . We say that the mappings A and S satisfy (E. A.) property if there exists a sequence
. We say that the mappings A and S satisfy (E. A.) property if there exists a sequence ![]() such that
such that
![]()
for some![]() .
.
Definition 8. [15] Let A and S be two self mappings defined on a metric space![]() . We say that the mappings A and S satisfy
. We say that the mappings A and S satisfy ![]() property if there exists a sequence
property if there exists a sequence ![]() such that
such that
![]()
3. Main Results
Now, we establish a common fixed point theorem for two pairs of weakly compatible mappings using E. A. property.
Theorem 1. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]() (1)
(1)
![]() (2)
(2)
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
If T(X) is closed then
1) The maps A and T have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B, S and T have an unique common fixed point.
Proof. Assume that the pair ![]() satisfy E. A. property, so there exists a sequence
satisfy E. A. property, so there exists a sequence ![]() such that
such that
![]() (3)
(3)
for some![]() . Since
. Since![]() , so there exists a sequence
, so there exists a sequence ![]() such that
such that![]() . Hence,
. Hence,
![]() (4)
(4)
From condition (2), we have
![]()
Taking limit as![]() , we get
, we get
![]()
Since
![]()
![]()
Therefore we have,
![]()
which is a contradiction, since![]() . Hence,
. Hence,![]() . Now, we have
. Now, we have
![]()
Assume ![]() is closed, then there exits
is closed, then there exits ![]() such that
such that![]() . We claim that
. We claim that![]() . Now, from condition (2)
. Now, from condition (2)
![]() (5)
(5)
Since
![]()
![]()
So, taking limit as ![]() in (5), We conclude that
in (5), We conclude that
![]() (6)
(6)
which is a contradiction. Hence,![]() . Now, we have
. Now, we have
![]() (7)
(7)
This proves that v is the coincidence point of![]() .
.
Again, since ![]() so there exists
so there exists ![]() such that
such that
![]()
Now, we claim that![]() . From condition (2)
. From condition (2)
![]()
which is a contradiction.
Hence, ![]()
Therefore,![]() .
.
This represents that w is the coincidence point of the maps B and S.
Hence,
![]()
Since the pairs ![]() and
and ![]() are weakly compatible so,
are weakly compatible so,
![]()
![]()
We claim![]() . From condition (2)
. From condition (2)
![]()
which is a contradiction.
Hence, ![]()
Therefore,![]() . Similary,
. Similary,![]() . Hence,
. Hence,![]() . This represents that u is the common fixed point of the mappings
. This represents that u is the common fixed point of the mappings ![]() and
and![]() .
.
Uniqueness:
If possible, let ![]() be other common fixed point of the mappings, then by the condition (2)
be other common fixed point of the mappings, then by the condition (2)
![]()
which is a contradiction.
Hence, ![]() This establishes the uniqueness of the common fixed point of four mappings.
This establishes the uniqueness of the common fixed point of four mappings.
From the above theorem, one can obtain the following corollaries easily.
Corollary 1. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
If T(X) is closed then,
1) The maps A and T have a coincidence point.
2) The maps A and S have a coincidence point.
3) The maps A, S and T have an unique common fixed point.
Corollary 2. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
If T(X) is closed then,
1) The maps A and S have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B and S have an unique common fixed point.
Corollary 3. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pair ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pair ![]() is weakly compatible.
is weakly compatible.
If S(X) is closed, then the mappings A and S have an unique common fixed point.
Now, we establish the following theorem.
Theorem 2. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]() (8)
(8)
![]() (9)
(9)
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
If T(X) is closed then,
1) The maps A and T have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B, S and T have an unique common fixed point.
Proof. Assume that the pair ![]() satisfy E. A. property, so there exists a sequence
satisfy E. A. property, so there exists a sequence ![]() such that
such that
![]() (10)
(10)
for some![]() . Since
. Since![]() , so there exists a sequence
, so there exists a sequence ![]() such that
such that![]() . Hence,
. Hence,
![]() (11)
(11)
From condition (9), we have
![]()
Taking limit as ![]() we get
we get
![]()
Since
![]()
![]()
Therefore we have,
![]()
which is a contradiction, since![]() . Hence,
. Hence,![]() . Now, we have
. Now, we have
![]()
Assume ![]() is closed, then there exits
is closed, then there exits ![]() such that
such that![]() . We claim that
. We claim that![]() . Now from condition (9)
. Now from condition (9)
![]() (12)
(12)
Since
![]()
![]()
So, taking limit as ![]() in (12), We conclude that
in (12), We conclude that
![]() (13)
(13)
which is a contradiction. Hence,![]() . Now, we have
. Now, we have
![]() (14)
(14)
This proves that v is the coincidence point of![]() .
.
Again, since ![]() so there exists
so there exists ![]() such that
such that
![]()
Now we claim that![]() . From condition (9)
. From condition (9)
![]()
Since
![]()
So if ![]() or
or ![]() we get the contradiction, since
we get the contradiction, since
![]()
or
![]()
Hence, ![]()
Therefore,![]() .
.
This represents that w is the coincidence point of the maps B and S.
Hence,
![]()
Since the pairs ![]() and
and ![]() are weakly compatible so,
are weakly compatible so,
![]()
![]()
We claim![]() . From condition (9)
. From condition (9)
![]()
Since
![]()
So if ![]() or
or ![]() or
or ![]() we get the contradiction. Since,
we get the contradiction. Since,
![]()
or
![]()
Hence, ![]()
Therefore,![]() . Similary,
. Similary,![]() . Hence,
. Hence,![]() . This represents that u is the common fixed point of the mappings
. This represents that u is the common fixed point of the mappings ![]() and
and![]() .
.
Uniqueness:
If possible, let ![]() be other common fixed point of the mappings, then by the condition (9)
be other common fixed point of the mappings, then by the condition (9)
![]()
Since
![]()
So if ![]() or
or ![]() or
or ![]() we get the contradiction, since
we get the contradiction, since
![]()
or
![]()
Hence, ![]() This establishes the uniqueness of the common fixed point of four mappings.
This establishes the uniqueness of the common fixed point of four mappings.
From the above theorem, we can establish the following corollaries:
Corollary 4. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
If T(X) is closed then
1) The maps A and T have a coincidence point.
2) The maps A and S have a coincidence point.
3) The maps A, S and T have an unique common fixed point.
Corollary 5. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pairs ![]() or
or ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
if T(X) is closed then
1) The maps A and S have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B and S have an unique common fixed point.
Corollary 6. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
![]() .
.
1) The pair ![]() satisfy E. A. property.
satisfy E. A. property.
2) The pair ![]() is weakly compatible.
is weakly compatible.
If S(X) is closed, then the mappings A and S have an unique common fixed point.
Now, we establish a common fixed point theorem for weakly compatible mappings using (CLR)-property.
Theorem 3. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]() (15)
(15)
![]() (16)
(16)
where,
![]() (17)
(17)
1) The pairs ![]() or
or ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
Then
1) The maps A and T have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B, S and T have an unique common fixed point.
Proof. Assume that the pair ![]() satisfy
satisfy ![]() property, so there exists a se- quence
property, so there exists a se- quence ![]() such that
such that
![]() (18)
(18)
for some![]() . Since
. Since![]() , so there exists a sequence
, so there exists a sequence ![]() such that
such that![]() . We show that
. We show that
![]() (19)
(19)
From condition (16), we have
![]() (20)
(20)
where
![]()
Taking limit as ![]() in (20), we get
in (20), we get
![]() (21)
(21)
Since
![]()
![]()
Hence, we have
![]()
which is a contradiction, since![]() .
.
Therefore,
![]()
Now we have
![]()
Assume![]() , then there exits
, then there exits ![]() such that
such that![]() .
.
We claim that![]() .
.
Now from condition (16)
![]() (22)
(22)
where
![]()
Since
![]()
![]()
So, taking limit as ![]() in (22), we conclude that
in (22), we conclude that
![]() (23)
(23)
which is a contradiction.
Hence,![]() .
.
This proves that v is the coincidence point of the maps B and S.
Therefore,![]() .
.
Since the pair (B, S) is weakly compatible, so
![]()
Since![]() , there exists a point
, there exists a point ![]() such that
such that ![]() We show that
We show that
![]()
From condition (16),
![]()
where,
![]()
Therefore,![]() .
.
![]()
This proves that u is the coincidence point of the maps A and T.
Since the pair ![]() is weakly compatible so,
is weakly compatible so,
![]()
We show that![]() .
.
From condition (16)
![]()
where
![]()
which is a contradiction.
Hence,![]() . Similarly, we obtain
. Similarly, we obtain![]() .
.
![]() . Hence, w is the common fixed point of four mappings
. Hence, w is the common fixed point of four mappings ![]() and
and![]() .
.
Uniqueness:
Let ![]() be other common fixed point of the mappings
be other common fixed point of the mappings ![]() and
and![]() , then by the condition (16)
, then by the condition (16)
![]() (24)
(24)
where
![]()
which is a contradiction.
Hence, ![]() This establishes the uniqueness of the common fixed point.
This establishes the uniqueness of the common fixed point.
Now we have the following corollaries:
Corollary 7. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pairs ![]() or
or ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
Then
1) The maps A and S have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B and S have an unique common fixed point.
Corollary 8. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pair ![]() and
and ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
Then
1) The maps A and T have a coincidence point.
2) The maps A and S have a coincidence point.
3) The maps A, S and T have an unique common fixed point.
Corollary 9. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pair ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pair ![]() is weakly compatible.
is weakly compatible.
Then
1) The maps A and S have a coincidence point.
2) The maps A and S have an unique common fixed point.
Now, we establish the following theorem.
Theorem 4. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]() (25)
(25)
![]() (26)
(26)
where
![]() (27)
(27)
1) The pairs ![]() or
or ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
then
1) The maps A and T have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B, S and T have an unique common fixed point.
Proof. Assume that the pair ![]() satisfy
satisfy ![]() property, so there exists a se- quence
property, so there exists a se- quence ![]() such that
such that
![]() (28)
(28)
for some![]() . Since
. Since![]() , so there exists a sequence
, so there exists a sequence ![]() such that
such that![]() . We show that
. We show that
![]() (29)
(29)
From condition (26), we have
![]() (30)
(30)
where
![]()
Taking limit as ![]() in (30), we get
in (30), we get
![]() (31)
(31)
Since
![]()
![]()
Hence, we have
![]()
which is a contradiction, since![]() .
.
Hence,
![]()
Now, we have
![]()
Assume![]() , then there exits
, then there exits ![]() such that
such that![]() .
.
We claim that![]() .
.
Now from condition (26)
![]() (32)
(32)
where
![]()
Since
![]()
![]()
So, taking limit as ![]() in (32) We conclude that
in (32) We conclude that
![]() (33)
(33)
which is a contradiction. Hence,![]() . This proves that v is the coincidence point of of the maps B and S.
. This proves that v is the coincidence point of of the maps B and S.
Hence,![]() .
.
Since the pair (B, S) is weakly compatible, so
![]()
Since ![]() there exists a point
there exists a point ![]() such that
such that ![]() We show that
We show that
![]()
From condition (26)
![]()
where
![]()
Hence
![]()
Since
![]()
So if ![]() or
or![]() , we get the contradic- tion for both cases.
, we get the contradic- tion for both cases.
Therefore,![]() .
.
![]()
This proves that u is the coincidence point of the maps A and T.
Since the pair ![]() is weakly compatible so,
is weakly compatible so,
![]()
We show that![]() .
.
From condition (26)
![]()
where
![]()
Since
![]()
So if ![]() or
or ![]() or
or
![]() we have
we have
![]()
which give contradictions for all three cases.
Hence,![]() . Similarly, we obtain
. Similarly, we obtain![]() .
.
![]() . Hence, w is the common fixed point of four mappings
. Hence, w is the common fixed point of four mappings ![]() and T.
and T.
Uniqueness:
Let ![]() be other common fixed point of the mappings
be other common fixed point of the mappings ![]() and T, then by the condition (26)
and T, then by the condition (26)
![]() (34)
(34)
where
![]()
Since
![]()
So if ![]() or
or ![]() or
or ![]() we have
we have
![]()
or
![]()
which give contradictions for all three cases.
Hence, ![]() This establishes the uniqueness of the common fixed point.
This establishes the uniqueness of the common fixed point.
Now, we have the following corollaries:
Corollary 10. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pairs ![]() or
or ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
Then
1) The maps A and S have a coincidence point.
2) The maps B and S have a coincidence point.
3) The maps A, B and S have an unique common fixed point.
Corollary 11. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pair ![]() and
and ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pairs ![]() and
and ![]() are weakly compatible.
are weakly compatible.
Then
1) The maps A and T have a coincidence point.
2) The maps A and S have a coincidence point.
3) The maps A, S and T have an unique common fixed point.
Corollary 12. Let (X, d) be a dislocated metric space. Let ![]() satisfying the following conditions
satisfying the following conditions
![]()
![]()
where
![]()
1) The pair ![]() satisfy CLR-property.
satisfy CLR-property.
2) The pair ![]() is weakly compatible.
is weakly compatible.
Then
1) The maps A and S have a coincidence point.
2) The maps A and S have an unique common fixed point.
Remarks: Our results generalize and extend the results of A. Amri and D. Moutawakil [14] , W. Sintunavarat and P. Kumam [15] in dislocated metric space.