Prediction of the Enhanced Out-of-Plane Thermal Conductivity of Carbon Fiber Composites Produced by VARTM ()
1. Introduction
Fiber based composites offer the unique ability to tailor material properties locally. Localized matrix or fiber architecture changes can meet local mechanical, electrical, or thermal loads within a component or vehicle, without the penalty of extra weight or the necessity to resort to additional external structures. Such integral materials reduce the number of components leading to not only more elegant designs, but also to structures that are less costly to manufacture. Local strength, stiffness, toughness, and thermal properties can be tailored by using carbon fibers and/or improved matrices. Numerous attempts have been made to increase the thermal conductivity of the matrix by adding high thermal conductivity solid fillers [1] . Zhou surveyed the effect of coupling agents on the thermal conductivity of epoxy resin loaded with Al-particles [2] . Lee et al. studied aluminum-nitride loaded epoxy resin [3] . He et al. and Gu et al. utilized boron nitride nanoparticles in epoxy composites [4] [5] . Hong et al. enhanced the thermal conductivity of epoxy composites with aluminum nitride and boron nitride fillers [6] . Ma et al. investigated carbon fiber epoxy resin composites filled with silicon carbide particles [7] . Kusunose et al. used nanofibers instead of particles to improve the thermal conductivity of epoxy resin [8] . Carbon nanotubes have frequently been used to increase thermal conductivities of resins. King et al. and Ma are cited exemplarily [9] [10] . A very contemporary approach consists of using graphene nanoplatelets to achieve this goal [11] [12] . However, to improve the thermal conductivity of the adhesives by a factor between 5 and 15, the above-mentioned fillers have to have a high enough load fraction, which would greatly affect their physical properties [13] - [15] . Especially the increase in viscosity above a threshold approximately 1 Pa・s prohibits the use of such resins for vacuum resin transfer molding [16] . Thus, Liang et al. used a volume fraction of only 0.1% of carbon nanofibers to increase the thermal conductivity of a carbon fiber composite plate in through-thickness direction produced by VARTM [17] . The 10% increase in thermal conductivity can only be regarded as marginal.
To further enhance the out-of-plane thermal conductivity of a composite plate or part, the fiber architecture has to be altered by introducing highly conductive carbon fibers in the out-of-plane direction. This can be done by different textile technology based procedures [18] :
Tufting;
Stitching;
Z-pinning;
3D-weaving.
Tufting and stitching are used on two-dimensional fabrics and thus are not suitable to introduce greater contents of z-fibers to the preform in the thickness direction without damaging the planar reinforcing fibers. Z-pinning is a technique to insert pins in thickness direction by mechanically forcing pins through the dry 2D-preform [19] . Nevertheless, although this procedure increases the in-plane delamination resistance, it has detrimental effects on planar reinforcing fibers.
3D-weaving is the only technology to manufacture a fabric with z-fibers of variable and higher contents (Figure 1). It has been proven suitable for such applications in the past [1] . However, it has either been tried to increase the thermal conductivity of the
![]() (a) (b)
(a) (b)
Figure 1.Schematic of 2D- and 3D-weaving process [1] .
matrix or the fiber architecture has been altered. A novel approach consists in combining both approaches. Thus, the objective of this research is to evaluate the suitability of the increase of the thermal conductivity by improving matrix conductivity and fiber architecture and its prediction.
2. Experimental
2.1. Materials
2.1.1. Resin
The matrix material was a cold-curing HP-E3000GL_SDB_resin with HP-E200GL_ SDB_hardener from HP-Textiles in which aluminum particles with an average diameter of 4 µm were distributed with a weight fraction of 7.5% corresponding with an Al-particle volume fraction of 3.6%. The thermal conductivity of this resin is given as 0.2 W/(m∙K) and of the aluminum as 170 W/(m∙K).
2.1.2. Fibers
For in-plane fibers, the Tenax®-E HTA40 E13 3K 200 tex fiber with a thermal conductivity of 17 W/(m∙K) is used. The out-of-plane fibers were high-modulus pitch-fibers from Mitsubishi (K13916 3K 2200 tex) with a thermal conductivity of 200 W/(m∙K). It was originally intended to utilize a pitch-fiber from Mitsubishi (K13D2U 2K 365 tex) with a thermal conductivity of 800 W/(m∙K) which was unfortunately not accessible.
2.2. 3D-Weaving
A 3D-weaving machine from the company MAGEBA (Figure 2(a)) was used to weave preforms with highly thermal high conductive carbon fibers in the out-of-plane direction. The in-plane fabric structure was designed similar to a plain weave with additional vertical yarns. The 3D-weaving-machine works with four shuttles to transport weft yarns. These shuttles are a special in-house development that avoids the frequent breakage of carbon fibers caused by twisting and bending of the yarn in commonly-used shuttles. However, the weaving process was only satisfactory stable with a z-fiber spacing of 6 mm and cabled pitch-fibers. Warp-yarns are attached to Jacquard-threads mounted on a Unival from Stäubli. Contrary to conventional Jacquard-devices, the Unival is able to lift the warp-yarns to four different height-positions with motors ca-
![]()
Figure 2. Textile machines used for sample manufacturing. (a) 3D weaving machine; (b) Braiding machine; (c) Braided roving.
pable to lift 160 g. From 1024 available Jacquard-threads, 750 were used to move the same number of the light Tenax-warp-yarns. 14 Jacquard-threads were attached to the 14 heavy pitch-carbon rovings. Preforms were made with attempted preform z-fiber contents 0%, 3% and 6%. The woven fabrics had the dimensions 140 × 140 × 5 mm.
2.3. Braiding
The high modulus pitch fibers used have an ultimate elongation of 0.4%. Thus, they are not primarily suitable to be processed by weaving or stitching due to the small bending radii incorporated by these methods. Braiding is used for a cabling process as known from carpet and tire industries. A supporting polyester thread was braided around the pitch-fiber roving [18] [20] . The braiding machine used was manufactured by Muratec Murata in Japan (Figure 2(b)). For the cabling process, it was necessary to implement twelve spools. The pulling speed of the roving was 0.263 m/min while the braider was spinning with a speed of 5.7 rev/min.
2.4. Vacuum Assisted Resin Transfer Molding
Six panels were produced by VARTM. Each panel contained either 0%, 3% or 6% of z-fibers and 0% or 3.6% Al-particles. The entire lay-up was assembled in accordance to Figure 3. Before infusion, the mixed resin was degassed in a pressure pot under vacuum for 10 min to reduce the air content in the resin. The maximum vacuum level was reached after a slow gradual decrease of pressure to avoid boiling of the resin. After degassing, ambient pressure was applied, forcing the resin to move into the still clamped inlet tube. Upon unclamping of the inlet, the resin flowed through the distribution media and impregnated transversely the preform. Once the flow front had reached the end of preform, the post-filling stage was initiated and pressure at the inlet and vent was set to 500 mbar. The laminate thickness and resin pressure gradients
![]() (a)
(a) ![]() (b) (c) (d)
(b) (c) (d)
Figure 3. Schematic diagram of stages in the VARTM infusion process [14] . (a) Lay up; (b) Pre-filling; (c) Filling; (d) Post-filling.
gradually dissipated, and the pressure boundary conditions were maintained until the resin was cured and subsequently post-cured at 65˚C.
It could be noticed that the Al-particles were filtered out within the first 10 mm of the flow path making these panels not worth for further consideration. Thus, a preform with no z-fibers was manufactured, allowing introducing the Al-particles directly into the preform. This preforms was infused as described above.
2.5. Sample Preparation
Four circular specimens with a diameter of 50 mm were cut out of each previously described infused panels by water-jet cutting. The panels had since been milled in order to create plano-parallel surfaces with accessible z-fibers (Figure 4). For additional comparison, two samples each were manufactured of neat resin discs and discs consisting of resin with 3.6 vol.-% Al-particles.
2.6. Thermal Conductivity Measurements
The thermal conductivity measurements were performed within a measuring cell (Figure 5) built in-house at the Institut für Kunststofftechnik Westpfalz according to ASTM E 1225-04, which allows measurements of circular samples with a diameter of 50 mm [21] [22] . Sample thicknesses can vary from 2 until 50 mm. Three thermistors in the top meter bar are used to measure heat flux which is assumed to be constant as the heat traveling through the sample and into the lower meter bar where a fourth temperature is read. Both meter bars are made out of stainless steel (kmat = 15.9 W/(m∙K). The top meter bar is insulated with foam and additionally shielded by a guard heater to prevent radial heat loss. The cell was placed on a water-cooled plate to provide a heat sink with a constant temperature Tsink beneath the bottom plate. Thermistor data were evaluated by a LabView-based program. Conductivity paste (OT-201 from Omega with k = 2.3 W/(m∙K)) was used in order to facilitate coupling and to reduce interfacial thermal resistance. The amount of coupling paste was weighed in order to apply a constant amount for each measurement. Comparing calibration measurements were performed on isotropic specimens to determine the accuracy of the measuring cell.
![]()
Figure 4. Exemplary sample with z-fiber for thermal conductivity measurements.
![]()
Figure 5. Measuring cell for thermal conductivity measurements.
3. Prediction of the Out-of-Plane Thermal Conductivity
3.1. Matrix
The thermal conductivity for a particle filled resin can be calculated for particle volume fraction up to 30% with a sufficient accuracy using a model suggested by Maxwell in the 19th century [23] .
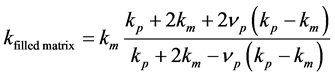 (1)
(1)
with ν P―particle volume fraction.
kp―thermal conductivity of particle.
km―thermal conductivity of matrix.
For a thermal conductivity of a particle much higher than that of the matrix (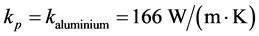 ,
, 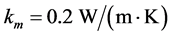 , Equation (1) can be simplified to
, Equation (1) can be simplified to
 (2)
(2)
More elaborate models have been published by Bruggemann, Cheng-Vachon, and Nielsen.
Bruggemann [24] :
 (3)
(3)
Cheng-Vachon [25] :
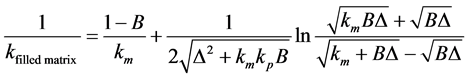 (4)
(4)
with
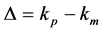 (5a)
(5a)
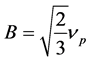 (5b)
(5b)
Nielsen [26] for dispersed hemispherical particles with data from [27] :
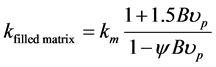 (6)
(6)
with
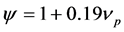 (7)
(7)
and
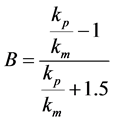 (8)
(8)
Other, very theoretical models have been developed. However, they are not practical to use [28] - [30] .
3.2. 3D-Fiber Assembly
The out-of-plane thermal conductivity for laminated and woven composites consists of contributions of vertical z-fibers plus the transverse thermal conductivity of the composite without vertical fibers. It can be approximated as a parallel connection of both components [19] .
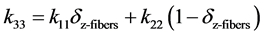 (9)
(9)
with δZ-Fibers = νFz/νF.
νFz―fiber volume fraction of z-fibers.
νF―fiber volume fraction of x-, y-, z-fibers.
k33―out-of-plane thermal conductivity of a 3D-woven fabric composite.
k11―longitudinal thermal conductivity of a laminated composite.
k22―transverse thermal conductivity of a laminated composite.
The longitudinal z-fiber contribution can be described according to the longitudinal thermal conductivity modeled by Thornburgh and Pears using the simple rule of mixture [31] .
![]() (10)
(10)
with kFa―axial fiber thermal conductivity.
The transverse thermal conductivity has been modeled by several researchers. A well accepted model was published by Hatta and Taya [32] .
![]() (11)
(11)
with kFr―radial thermal conductivity of fiber.
It has been found out that Equation (9) overestimates the thermal conductivities of composite samples with fibers of high thermal conductivity in perpendicular direction [19] [33] . Three different effects due to the presence of high conductive heat flux entry points could be identified for consideration:
Distribution of the high conductive areas (number of entry points)
Thermal conductivity of an attaching material to deviate an incoming homogeneous heat flux into an inhomogeneous one (or vice versa for an existing heat flux)
Thickness of composite part or sample
![]() (12)
(12)
with ξKmat―material factor.
ξTD―thickness-grid density factor.
![]() (13)
(13)
![]() (14)
(14)
with kmat―Thermal conductivity of adjacent material.
tsample―thickness of composite part or sample.
drov―diameter of roving.
3.3. Application of Models
The thermal conductivity of the loaded resin was calculated using the Equations (2)-(8) with particle volume content of νp = 3.6%. All models delivered quite similar results (Table 1).
The out-of-plane thermal conductivity k33 can be predicted according to Equations (9)-(14). One key parameter to obtain high k33-values is the z-fiber content, which depends on the distance between the z-fibers as shown in Figure 6.
With the parameters given above, the out-of-plane thermal conductivity was calculated depending on the distance between the z-fibers for a 5 mm thick sample and matrix conductivities for neat resin (km = 0.2 W/m∙K) and resin loaded with 3.6% Al-par- ticles (Table 1). It turns out that the impact of the matrix loading on the out-of-plane-
![]()
Table 1. Calculated matrix’ thermal conductivity km using different models.
![]()
Figure 6. Dependency of z-fiber volume fraction on z-fiber spacing.
thermal conductivity is about 0.1 W/(m∙K) higher than for neat resin and is thus negligible for higher z-fiber contents. As depicted in Figure 7, an out-of-plane thermal conductivity of about 4 W/(m∙K) can be achieved with a spacing of 6 mm resulting in a z-fiber content of 6.3%.
4. Comparison between Measured and Calculated Values
The thermal conductivity measurements yielded the following results as shown in Table 2.
Measured and predicted thermal conductivity values for the out-of-plane direction correspond quite well. The measured thermal conductivity of the neat resin agrees well with the data given by the manufacturer of the resin of 0.2 W/(m∙K) which proves the accuracy of the measuring device used. The thermal conductivities of the composite samples are slightly lower than predicted which can be caused by fibers not having a proper thermal contact due to an insulating resin film and broken fibers due to the weaving process.
5. Conclusions and Perspectives
It has been shown that reinforcing fabrics in thickness direction with high thermally conductive pitch carbon fibers is a viable method to increase the out-of-plane thermal conductivity of a carbon composite material. Due to the high impact of the z-fiber conductivity on the out-of-plane conductivity, the influence of a loaded matrix is marginal. Moreover, the infusion of preforms in the usual way with loaded resins is almost not possible due to filtering effects. Thus, it can be concluded that if introducing highly conductive z-fibers, the use of a particle filled resin is not necessary and furthermore should be avoided due to the manufacturing problems mentioned above.
The single models introduced in a combined approach to predict the out-of-plane thermal conductivity of a 3D-woven fabric agree well with the measured values. In case of using the K13D2U 2k fiber from Mitsubishi with a thermal conductivity of 800
![]()
Figure 7. Dependency of out-of-plane thermal conductivity k33 on z-fiber spacing.
![]()
Table 2. Results of measured and predicted thermal conductivities.
W/(m∙K), which has the same ultimate elongation as the fiber used, an out-of-plane thermal conductivity of more than 15 W/(m∙K) can be predicted while maintaining the same fiber spacing and thus z-fiber volume fraction. This should be proven experimentally once these fibers are accessible.
Using newly developed shuttles, the weaving process with very brittle but cabled pitch fibers was possible. This approach has to be followed and smaller spacings between z-fibers should be produced by 3D-weaving.
Acknowledgements
Thanks are due to the German Science Foundation (DFG), which supported financially the acquisition of the 3D-weaving machine financially (INST 252/9-1) and the AiF Arbeitsgemeinschaft industrieller Forschungsvereinigungen “Otto von Guericke” e.V. for financial support through the ZIM-project KF2161903PK1 to develop a shuttle for weaving carbon fibers.