Continuum Constitutive Modeling for Isotropic Hyperelastic Materials ()
Received 17 June 2016; accepted 30 July 2016; published 2 August 2016

1. Introduction
Many materials with wide-ranging applications, including rubbers, thermoplastic elastomers, and biological tissues, can be characterized as isotropic hyperelastic materials. Constitutive models play an important role in design and analyses. The established models have been classified into two main categories: micro-mechanical and phenomenological. Micro-mechanical models include 3-chain, 8-chain, Unit sphere, Full-network, Flory-Erman, Tube, and Extended tube. Phenomenological models can be subdivided into two groups: stretch-based and invariant-based. Stretch-based phenomenological models cover Ogden, Shariff, and Attard models. Invariant-based phenomenological models include Neo-Hooke, Mooney-Rivlin, Isihara, Gent-Thomas, Swanson, Yeoh, Arruda- Boyce, Gent, Yeoh-Fleming, Carroll, Hart-Smith, Alexander, van der Waals, Pucci-Saccomandi, and Lopez- Pamies models. The established models have been thoroughly reviewed and evaluated by Boyce and Arruda (2000) [1] , Steinmann, Hossain, and Possart (2012) [2] , and Hossain and Steinmann (2013) [3] . Current multi- scale approaches for modeling rubber-like materials and soft tissues have been briefly reviewed and compared with classical macroscopic phenomenological models by Puglisi and Saccomandi (2016) [4] .
For constitutive models, great progress has been made in continuum mechanics. The thermodynamic foundations of constitutive equations at finite strains are archived in the classic treatise on continuum mechanics by Truesdell and Noll (1965) [5] . Advanced mathematical foundations of elasticity are presented in monographs by Marsden and Hughes (1983) [6] , Ogden (1984) [7] , and Holzapfel (2000) [8] .
For isothermal and adiabatic processes, the stored energy function, Ψ, is a function of the right Cauchy-Green tensor, C, as
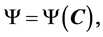 (1)
(1)
in which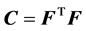 , and F is the deformation gradient tensor.
, and F is the deformation gradient tensor.
With Clausius-Duhem inequality, the second Piola-Kirchhoff stress tensor, S, takes the form of
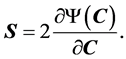 (2)
(2)
When hyperelastic materials under deformation are isotropic, the stored energy function depends on the invariants of the right Cauchy-Green tensor, which was established by the classical work of Rivlin (1948) [9]
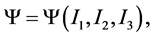 (3)
(3)
in which the three invariants, I1, I2, and I3, of right Cauchy-Green tensor are given by
 (4)
(4)
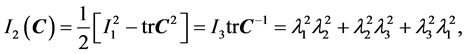 (5)
(5)
 (6)
(6)
where 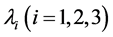 are principal stretches in three mutually orthogonal directions.
are principal stretches in three mutually orthogonal directions.
Substituting (3) into (2) and using the chain rule of differentiation yields
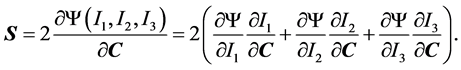 (7)
(7)
The derivatives of the three invariants with respect to C are given by the following three equations, respectively
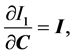 (8)
(8)
 (9)
(9)
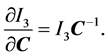 (10)
(10)
Substituting the derivatives (8), (9), and (10) into constitutive Equation (7) produces the most general form of a stress as a function of the three invariants for isotropic hyperelastic materials under finite strains
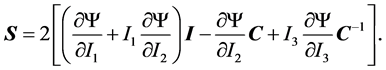 (11)
(11)
For a tangent operator, a fourth-order elasticity tensor, 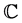 , is usually introduced to relate changes in stress dS and changes in the right Cauchy-Green tensor dC through
, is usually introduced to relate changes in stress dS and changes in the right Cauchy-Green tensor dC through
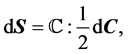 (12)
(12)
where the fourth-order elasticity tensor is written as
![]() (13)
(13)
The most general fourth-order elasticity tensor in terms of the three principal invariants of the right Cauchy- Green tensor is documented by Holzapfel (2000) [8]
![]() (14)
(14)
where the fourth-order tensors![]() ,
, ![]() , and
, and ![]() are given by
are given by
![]() (15)
(15)
![]() (16)
(16)
and where ![]() and
and ![]() are fourth-order zero and unit tensors, and the parameters
are fourth-order zero and unit tensors, and the parameters ![]() are defined by
are defined by
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Although the second Piola-Kirchhoff stress tensor (11) and the fourth-order elasticity tensor (13) are the fundamental constitutive equations in the theory of finite hyperelasticity, the stored energy function, Ψ, is the key to determining all of them. Thus, the main objective is to establish, solve, and apply the stored energy function to construct a general constitutive model for isotropic hyperelastic materials.
2. Constitutive Modeling for Isotropic Hyperelastic Materials
For a general isotropic hyperelastic constitutive model based on the theory of continuum mechanics, the partial differential equation of a stored energy function has been postulated and derived. Once the partial differential equation is solved and the function is determined, the constitutive model can be obtained under several geometric conditions.
2.1. Stored Energy Partial Differential Equation
A stored energy at a finite deformation is postulated to be equal to its stress work done. The invariant of the right Cauchy-Green tensor-based stored energy function can be formulated by
![]() (21)
(21)
Substituting (11) into (21) generates
![]() (22)
(22)
Expanding (22) with ![]() gives
gives
![]() (23)
(23)
Eliminating the right Cauchy-Green tensor related terms with (4)1, (5)1, noticing![]() , and rearranging, yields the following partial differential equation
, and rearranging, yields the following partial differential equation
![]() (24)
(24)
Now, the partial differential equation for the stored energy function (24) has been simplified into a function of three scalar invariants. The stored energy partial differential equation can generally be solved by Lie group methods.
2.2. General Solution for Stored Energy Function
Based on Lie group methods documented by Ibragimov (2009) [10] , the characteristic system for the stored energy partial differential Equation (24) reads
![]() (25)
(25)
Taking its three first-integrals![]() ,
, ![]() , and
, and![]() , the general solution to (24) can be solved and written as
, the general solution to (24) can be solved and written as
![]() (26)
(26)
where f and g are two arbitrary functions.
2.3. Model for Isotropic Hyperelastic Materials
The general solution (26) has two arbitrary functions to be determined for practical applications. For isotropic hyperelastic materials, translational, rotational, and ellipsoidal deformations are indispensable. Thus, the curvatures of the three types of deformations are used as geometric conditions to select the two arbitrary functions.
2.3.1. A Particular Solution for Stored Energy Function
For the accurate representation of a translational deformation and a rotational deformation, the first arbitrary function, f, is selected as
![]() (27)
(27)
In order to accurately describe an ellipsoidal deformation, a simple inverse function is required. Thus, the second arbitrary function, g, is chosen as
![]() (28)
(28)
Substituting (27) and (28) into (26) gives the particular solution of the stored energy function
![]() (29)
(29)
where the three coefficients, c1, c2, and c3, are unknown constants to be determined by experimental tests.
2.3.2. Stress and Elasticity Tensors
Stress and elasticity tensors are indispensable elements in constitutive models for numerical solutions of boundary value problems by iterative approaches such as Newton-Raphson methods.
Applying the general stress Equation (11) to the particular solution (29) gives the specific second Piola- Kirchhoff stress tensor
![]() (30)
(30)
The eight parameters for the elasticity tensor have been worked out by substituting the particular solution (29) into (17) through (20)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
Seven out of eight parameters are non-zeros and therefore the particular solution is relatively general.
2.3.3. Geometric Interpretations of Particular Solution
Geometric interpretations of the three terms in the particular solution can also be revealed through the second Piola-Kirchhoff stress tensor and the elasticity tensor. The term with the coefficient c1 only appears in the second Piola-Kirchhoff stress tensor Equation (30), describing a constant modulus but does not show up in the parameters for the elasticity tensor, meaning that the curvature of a deformation is zero due to principal translational deformations. The term related to the coefficient c2 models the curvatures of rotational deformations. The term involving the coefficient c3 captures the curvature of an ellipsoidal deformation, coupling a volumetric or dilatational deformation and an isochoric or distortional deformation. Specific equations for the mean curvature of a general spacial surface and the Gaussian curvature of an ellipsoid can be found in the classic monograph of differential geometry by Carmo (1976) [11] . Nevertheless, ellipsoidal deformations preserve numerical stabilities.
The particular solution as a constitutive model is applicable to both incompressible and compressible isotropic hyperelastic materials. The current model will be used to fit the experimental data of vulcanized rubber containing 8% sulfur by Treloar (1944) [12] , Entec Enflex S4035A thermoplastic elastomer (TPE), and a slightly compressible rubber material.
3. Model Validation
Several experimental test methods can be used to characterize hyperelastic materials. Most commonly used methods are uniaxial tension, uniaxial compression, equibiaxial tension, pure shear, and confined volumetric tests in which detailed reviews are given by Charlton, Yang, and Teh (1994) [13] . In experiments, nominal stresses and stretches are usually recorded. The three principal nominal stresses in terms of a stored energy function and principal stretches are given by
![]() (34)
(34)
3.1. Modeling for Different Deformation Modes
In order to validate the continuum constitutive model (29), the nominal stress, the first Piola-Kirchhoff stress, as the function of principal stretches of uniaxial tension, pure shear, equibiaxial tension, and confined volumetric tests will, respectively, be derived for the continuum model.
3.1.1. Uniaxial Tension Test
In a uniaxial tension test, we have ![]() and
and ![]() based on the incompressible condition of
based on the incompressible condition of![]() . Thus, the first two invariants for the uniaxial tension deformation mode are
. Thus, the first two invariants for the uniaxial tension deformation mode are
![]() (35)
(35)
Substituting (35) into (29), and then into (34) gives
![]() (36)
(36)
3.1.2. Pure Shear Test
In a pure shear test, ![]() ,
, ![]() , and
, and ![]() since
since![]() . Thus, the first two invariants for the pure shear deformation mode are the same
. Thus, the first two invariants for the pure shear deformation mode are the same
![]() (37)
(37)
Substituting (37) into (29), and then into (34) generates
![]() (38)
(38)
3.1.3. Equibiaxial Tension Test
In an equibiaxial tension test, we have ![]() and
and ![]() from
from![]() . Thus, the first two invariants for equibiaxial tension deformation mode are
. Thus, the first two invariants for equibiaxial tension deformation mode are
![]() (39)
(39)
Substituting (39) into (29), and then into (34) yields
![]() (40)
(40)
3.1.4. Confined Volumetric Test
In a confined volumetric test, we have simply ![]() and
and![]() . Thus, the three invariants for the volumetric deformation mode are
. Thus, the three invariants for the volumetric deformation mode are
![]() (41)
(41)
Substituting (41) into (29), and then into (34) produces
![]() (42)
(42)
3.2. Fitting Continuum Model to Experimental Data
First, Treloar’s uniaxial tension experimental data has been chosen to fit the uniaxial tension model (36) by a linear least square method. The total squared error between the model and experiment is given by
![]() (43)
(43)
where ![]() is experimental engineering stress data in uniaxial tension tests and n is the total number of pairs of experimental data. The error,
is experimental engineering stress data in uniaxial tension tests and n is the total number of pairs of experimental data. The error, ![]() , can be minimized with the following conditions
, can be minimized with the following conditions
![]() (44)
(44)
Substituting (36) into (43), and applying (44) yields
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
where
![]() (48)
(48)
Numerically solving (45), (46), and (47), along with (48), simultaneously obtains the three coefficients as c1 = 0.1409441 MPa, c2 = 0.1425925 MPa and c3 = 3.1970322 × 10−7 MPa. The comparison between the continuum model and Treloar’s uniaxial tension test is shown in Figure 1. The continuum model is excellently suited to fit Treloar’s uniaxial tension test. To further demonstrate the predictive capacity of the continuum model, the three coefficients obtained from fitting Treloar’s uniaxial tension test have been used in both the pure shear Equation (38) and the equibiaxial tension Equation (40). The predictions of Treloar’s pure shear and equibiaxial tension tests are shown in Figure 2 and Figure 3, respectively. The pure shear prediction results are quite accurate. For Treloar’s equibiaxial tension test, however, the model’s prediction is slightly higher than experimental data at larger stretches.
By the same token, the three coefficients of c1 = 0.1027292 MPa, c2 = 0.0310506 MPa and c3 = 2.0345028 × 10−7 MPa have been obtained for the Entec Enflex S4035A TPE material. The comparison between the current model and the TPE uniaxial tension test is shown in Figure 4. The continuum model is also excellently suited for fitting the TPE uniaxial tension test. The predictions of pure shear and equibiaxial tension tests for the TPE are shown in Figure 5 and Figure 6, respectively. The pure shear prediction results are very accurate. For the equibiaxial tension test data, however, the model’s prediction is slightly lower than experimental data at all corresponding stretch levels.
For slightly compressible isotropic hyperelastic materials, a confined volumetric test is usually conducted. With (41) and (42), the confined volumetric test of a rubber material has similarly been fitted by the continuum hyperelastic model and shown in Figure 7. As the testing compressive stress increases from 0 to 315 MPa, the corresponding unit volume change increases from 0 to 0.0807. The three constants of c1 = −22382.19487 MPa,
![]()
Figure 1. Comparison between model and Treloar’s uniaxial tension test.
![]()
Figure 2. Model prediction for Treloar’s pure shear test.
![]()
Figure 3. Model prediction for Treloar’s equibiaxial tension test.
![]()
Figure 4. Comparison between model and uniaxial tension test of S4035A TPE.
![]()
Figure 5. Model prediction for pure shear test of S4035A TPE.
![]()
Figure 6. Model prediction for equibiaxial tension test of S4035A TPE.
![]()
Figure 7. Comparison between model and confined volumetric test.
c2 = 32856.28089 MPa, and c3 = 126.40171 MPa have been obtained for the confined volumetric test model (42) and the most complete form of the stored energy function (29).
4. Discussion
The most important concept to notice about hyperelastic materials is that its deformation is not directly proportional to the applied load in which it exhibits a nonlinear behavior. For hyperelastic materials, independent load paths are usually assumed. This behavior, however, is only approximately observed in many hyperelastic materials in Belytschko, Liu, and Moran (2000) [14] . The independent load path is only applicable to linear elastic materials. In the continuum constitutive modeling of isotropic hyperelastic materials (21), independent load paths are irrelevant.
The invariant of stain-based stored energy function can be postulated and formulated by a double contraction of the second Piola-Kirchhoff stress tensor and the Green-Lagrange strain tensor as
![]() (49)
(49)
Equation (49) has also been solved by Lie group methods, which results in
![]() (50)
(50)
where q and r are also two arbitrary functions. When the three invariants of Green-Lagrange strain tensor, ![]() ,
, ![]() , and
, and![]() , are used, Equation (50) takes the same form of Equation (26) in
, are used, Equation (50) takes the same form of Equation (26) in
![]() (51)
(51)
The five strain measures were unified in terms of stretches with![]() , in which i = 1, 2, 3, by Seth (1964) [15] . In the cases of n = −2, −1, 0, 1, and 2, it gives Almansi, Swainger, Hencky, Cauchy, and Green- Lagrange strains, respectively. A stretch is ubiquitous in the strain measures. Compared to strains, not only do stretches capture the characteristics of a deformation but they also avoid singularities and imaginary numbers in constitutive modeling. Thus, the invariant of stretch-based solution is more appropriate in establishing a constitutive model for isotropic hyperelastic materials.
, in which i = 1, 2, 3, by Seth (1964) [15] . In the cases of n = −2, −1, 0, 1, and 2, it gives Almansi, Swainger, Hencky, Cauchy, and Green- Lagrange strains, respectively. A stretch is ubiquitous in the strain measures. Compared to strains, not only do stretches capture the characteristics of a deformation but they also avoid singularities and imaginary numbers in constitutive modeling. Thus, the invariant of stretch-based solution is more appropriate in establishing a constitutive model for isotropic hyperelastic materials.
Deformations of hyperelastic materials in experimental tests could be coupled with boundary, geometric, and material nonlinearities. In uniaxial compression tests, experimental results are usually overestimated due to inhomogeneous deformations and hydrostatic pressure effects [16] . The inhomogeneous deformations and hydrostatic pressure effects are mainly resulted from boundary nonlinearities in which a friction force is exerted on contact surfaces of samples. In equibiaxial tension tests, albeit no friction, inhomogeneous deformations and hydrostatic pressure effects under a limited amount of deformation do exist, causing overestimated experimental results such as the equibiaxial tension test of the S4035A TPE shown in Figure 6. In general, equibiaxial tension tests cannot match the accuracy and the amount of a deformation in uniaxial tension tests.
In the general solution (26) of stored energy function, Ψ, there are two functions, f and g, that look relatively arbitrary. What is not arbitrary, however, is the framework of the solution. It is worth noticing that all terms are in the order of λ2 even though they are already dimensionless. The continuum constitutive model (29) has been derived from the general solution of the stored energy partial differential equation, which is suitable for both incompressible and compressible isotropic hyperelastic materials. The continuum model fits various modes of deformation using the data obtained from a uniaxial tension test only for the tested incompressible hyperelastic materials. This leads to a reduced number of requirements on material testing.
5. Conclusions
The partial differential equation for isotropic hyperelastic constitutive models has been postulated and derived from the balance between stored energy and stress work done. The stored energy as a function of three invariants of the right Cauchy-Green tensor has then been solved by Lie group methods.
Although the invariant of the Green-Lagrange strain based stored energy function has also been obtained, singularities and imaginary numbers have yet to be overcome for practical applications. Since stretches avoid singularities and imaginary numbers, it is the most appropriate variable for establishing a continuum constitutive model.
The general solution can be applied to constitutively model isotropic hyperelastic materials. A three-term particular solution (29) for stored energy function has, then, been extracted from the general solution (26). The stress and elasticity tensors reveal geometrical interpretations of different types of deformations. The I1c1 term monitors principal translational deformations; the ![]() term captures curvatures of rotational deformations; and the
term captures curvatures of rotational deformations; and the ![]() term describes curvatures of ellipsoidal deformations.
term describes curvatures of ellipsoidal deformations.
The three coefficients, c1, c2, and c3, have been determined by a linear least square method using uniaxial tension data and applied to predict pure shear and equibiaxial tension data for incompressible materials, such as the rubber and the TPE. The continuum model is equally applicable to slightly compressible materials, such as the selected rubber material. Excellent agreements between the continuum model and the experiments have been achieved.
The versatile continuum model fits various modes of deformations from uniaxial tension tests for isotropic hyperelastic materials since tensile tests provide sufficient accuracy for multiple modes of deformations at all stretch levels. This leads to minimal requirements needed for material testing.
Acknowledgements
The author is grateful to Prof. Alan C.W. Lau for guiding him into the field of mechanics of materials and encouraging his persistent efforts in scientific research and to reviewers for their constructive suggestions to improve the quality of this paper.
He would also like to express gratitude to his family, Jianming and Jiesi Zhao, for their encouragement, support, and help.