Flow-Accelerated Corrosion in Pipe Wall Downstream of Orifice for Water and Air-Water Bubble Flows ()
Received 2 February 2016; accepted 21 June 2016; published 13 July 2016

1. Introduction
The flow-accelerated corrosion (FAC), liquid droplet impingement (LDI) corrosion, and cavitation erosion (C/E) occurring in the piping system of power plants, and chemical plants, are serious problems because they lead to damage in the piping system.
An orifice is used widely as a flow meter or contraction device in a piping system in various plants because of its simple construction, high reliability, and low cost. It is well known that FAC occurs in a pipe wall downstream of the orifice. In fact, the accident that took place in the power plants, etc. was caused by FAC damage in pipes [1] - [5] . Chexal [1] investigated the FAC in power plant. Dooley and Chexal [2] investigated the effect of water chemistry on FAC. Poulson [3] investigated complexities in predicting erosion corrosion in an elbow and after an orifice. At the Mihama nuclear power plant, Japan, the pipe wall (diameter D = 560 mm) downstream of the orifice with an area contraction ratio of CR = 0.36 was broken by FAC after 21 years of use under the following conditions: flow rate of water Qw = 100 ton/hour, mean velocity um ≈ 2.2 m/s, pressure p = 0.93 MPa, and temperature T ≈ 142˚C [4] [5] .
The FAC has been studied from the viewpoint of material science, electrochemistry, and fluid dynamics [1] - [17] . The mechanism of occurrence has also been examined by considering the relationship between mass transfer and flow velocity, but this has not been fully elucidated.
In addition, Yoneda, et al. [4] [5] and Shakouchi, et al. [11] [15] found that the wall thinning rate can be expressed by the turbulent kinetic energy near the pipe wall and the pressure fluctuation on the pipe wall downstream of the orifice, respectively. The pressure fluctuation exerts repeated variable force on the pipe wall.
It has been shown that there is a good correlation between the pipe wall thinning rate TR and the turbulent kinetic energy k near the pipe wall as shown in Sections 1.1 and 1.2 or the pressure fluctuation p’ on the pipe wall downstream of the orifice for single-phase, water flow.
In this study, the flow accelerated corrosion (FAC) in a pipe wall downstream of the orifice is examined phenomenologically. In particular, FAC for a two-phase air-water bubble flow is examined experimentally and compared with that of a single-phase water flow. Further, it is shown that because p’ is also considered a governing parameter of FAC for a two-phase air-water bubble flow [11] [15] , TR can be estimated using p’. It is also indicated that, by using a downstream pipe with a smaller diameter than that of the upstream pipe, p’ or TR can be suppressed.
1.1. Wall Thinning Rate, Turbulent Kinetic Energy and Wall Shearing Rate for Water Flow
Figure 1 shows the variation of wall thinning rate distribution TR [mm/year] on the pipe downstream if the orifice and turbulent kinetic energy distribution k[m2/s2] at location 0.2D (D = 100 mm) separated from the pipe wall, as measured in earlier experiments for the Pipe line A and B of the Mihama nuclear power plant [4] [5] . Yoneda and Morita [4] [5] mentioned that TR depends on k near the pipe wall and Utanohara et al. [9] concluded that TR depends on the wall shearing stress, τ.
1.2. Relation between Wall Thinning Rate and Turbulent Kinetic Energy for Water Flow
Figure 2 shows the relation between TR and k derived from Figure 1 [16] . The TR is well approximated by the following linear function k, where the correlation coefficient R of the pipe-lines A and B are 0.97 and 0.95, respectively.

Phenomenologically, the TR can be well correlated with k [4] [5] which means TR can be decreased by decreasing k. However, because the measurement of k and τ is very complicated, some of the authors suggest that k and τ are conceptually related with pressure fluctuation p’ on the pipe wall [11] [15] [18] - [20] , which is then related with TR. Thus the TR can be estimated by p’ [11] [15] .
2. Experimental Apparatus and Procedure
Figure 3 shows the schematic diagram of the experimental apparatus. A submersible pump ② was used to send the required amount of tap water through an electromagnetic flow meter (Hitachi High-Tech Control Systems Co., Ltd., FMR104W) ⑤ into the pipe test section with diameter of D = 40.0 mm. The pipe test section was made of transparent acrylic resin with total length of L = 2650 mm and was set vertical. The air from the compressor ⑧ is mixed into the water flow by passing through the bubble generator ⑩ made of porous fine ceramics set at the bottom of the test section. The flow rate of air was measured and controlled by flow meter ⑨ and control valves. As a result, the flow becomes a two-phase gas-liquid bubble flow and after flowing in the test section only the water flows back to the water tank ①. The water in the tank was continuously renewed in order to maintain the water at a constant temperature. An orifice ⑦ was set at 40D downstream of the inlet of the test section.
The mean and fluctuating pressure distributions on the pipe wall up-stream and down-stream of the orifice were measured by small pressure holes (diameter of 0.8 mm), a water column manometer, and a semi-conductor type small pressure transducer (JTEKT, PD104SW-100K). The related pressure and primary resonance frequency of the transducer is 100 kPa and more than 6 kHz, respectively. The measurement time of the pressure fluctuation p’ was 2.5 s, and the sampling frequency was 1.0 kHz, and the mean value of 10 measurements was used. The dominant frequency of p’ was approximately 6 ~ 8 Hz in the present study.
Figure 4(a) shows a standard orifice (according to JIS Z8762, hereafter referred to as “Std”). The contraction area ratio CR of the orifice was 0.36. The inner diameters of the nozzle and the pipe were constant at d = 24.0 mm and D = 40.0 mm, respectively. The plate thickness was t = 4.0 mm, and the clearance angle of the outflow was constant at 45˚. Another Std-rev orifice which reversed the direction of the Std orifice was also used to reduce flow fluctuation downstream of the orifice.
![]()
Figure 1. Wall thinning rate TR [mm/year] and turbulent kinetic energy k [m2/s2] distribution [4] [5] .
![]()
Figure 2. Wall thinning rate TR vs. Turbulent kinetic energy k [16] .
![]()
Figure 3. Schematic diagram of experimental apparatus.
Furthermore, one more Std nozzle with downstream pipe diameter of Dp < D = 40.0 mm was used with reference Std-Dp orifice as shown in Figure 4(b). This aims to suppress p’ or TR.
3. Results and Discussions
3.1. Flow Rate Coefficient of Orifice and Pressure Fluctuation for Single Phase (Water) Flow
3.1.1. Flow Characteristics of Orifice and Flow Rate Coefficient
In order to use an orifice as a flow meter or a contraction it is needed to make clear the flow characteristics of the orifice. In this section, the flow characteristics of orifice of Std, Std-rev and Std-Dp (Dp = 35.2 mm so that CR = 0.36) are examined in terms of flow rate coefficient.
The flow rate coefficient, C, of an orifice is defined by
 (3)
(3)
where, A0 is the cross-sectional area of orifice hole, Q is the volumetric flow rate, and (p1 − p2) is the flow resistance of the orifice.
Figure 5 shows the flow rate coefficient, C, of the test orifice with area contraction ratio of CR = 0.36. The flow resistance (p1 − p2) of the orifice was obtained as the pressure difference derived from the linear pressure distributions following the Blasius relation [16] at upstream and downstream of the orifice. The flow rate coefficient of the standard orifice, Std, is C = 0.687, which is constant in Re = (1.0 ~ 6.5) × 104. This was consistent with the standard value and error range of less than ±0.5% provided by the JIS.
The pressure fluctuation, p’, of the Std-rev orifice is smaller than that of Std one because the inflow is smoother. Nevertheless, C is larger than in Std orifice and the flow resistance becomes smaller. This means that to measure the same flow rate with the same accuracy, a more accurate measurement of the flow resistance (p1 − p2) is needed.
3.1.2. Pressure Fluctuation
Figure 6 shows an example of the pressure fluctuation, p’, on the pipe wall downstream of the Std and Std-rev orifices. The CR is 0.36 and Re number is 5 × 104. The p’ of Std increases with downstream distance and takes the maximum value p’max around y/D ≈ 1.6. The p’max of Std-rev is about 9% smaller than that of Std and the y position of p’max shifts to y/D ≈ 2.0.
Figure 7 shows the time variation of pressure on the pipe wall at y/D = 1, 2, 3, and 4. The pressure at each position fluctuates with time and the amplitude at y/D = 2.0 is the largest in this case.
Figure 8 shows the relation between power spectrum density, PSD, and fluctuation frequency f of the pres-
![]()
Figure 5. Flow rate coefficient, C (CR = 0.36).
![]()
Figure 6. Pressure fluctuation p’ of Std and Std-rev (CR = 3.6, Re = 5.0 × 104).
![]()
Figure 7. Time variation of pressure p of Std.
sure fluctuation obtained by FFT analysis. The dominant frequency is observed 5 Hz and the y position of the maximum PSD is at y/D = 2.0.
As mentioned earlier, the profile of p’ of Std orifice is consistent with that of the wall thinning rate, TR. Figure 9 shows their relation in which their correlation factors of Pipe-lines A and B were 0.87 and 0.85, respectively. Since it can be said that there is a strong correlation between the TR and p’ the TR can be estimated by p’. The maximum pressure fluctuation  of the Std-rev orifice is about 9% smaller than that of the Std orifice and the TR can be decreased.
of the Std-rev orifice is about 9% smaller than that of the Std orifice and the TR can be decreased.
Figure 10 shows one example of the variation of p’ of Std-Dp with downstream pipe diameter Dp [11] . In this figure, the curve at Dp = 40.0 mm is equivalent to the Std orifice. The overall value of p’ becomes smaller and decreases the Dp from 40.0 to 35.2 mm. It is therefore considered that the confinement of the flow by a smaller pipe diameter downstream of the orifice promote the decrease in the pressure fluctuation.
Figure 11 shows the relation between 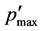 and Dp of the Std-Dp orifice. Accordingly, the maximum pressure fluctuation
and Dp of the Std-Dp orifice. Accordingly, the maximum pressure fluctuation 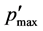 can be approximated by using polynomial function of Dp.
can be approximated by using polynomial function of Dp.
 (4)
(4)
The 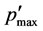 decreases with a reduction in Dp, and the
decreases with a reduction in Dp, and the ![]() of Std-Dp orifice at Dp = 35.2 mm decreases with Dp = 35.2 mm, decreases approximately 16% of the Std orifice. That is, this Std-Dp orifice can decrease p’ or
of Std-Dp orifice at Dp = 35.2 mm decreases with Dp = 35.2 mm, decreases approximately 16% of the Std orifice. That is, this Std-Dp orifice can decrease p’ or ![]() under the same flow resistance as the Std orifice. This means that Std-Dp can decrease FAC or wall thinning downstream of the orifice maintaining the functionality of the orifice.
under the same flow resistance as the Std orifice. This means that Std-Dp can decrease FAC or wall thinning downstream of the orifice maintaining the functionality of the orifice.
3.2. FAC for Two-Phase Gas-Liquid (Air-Water) Bubble Flow
3.2.1. Flow Pattern and Bubble Size
Figure 12 shows an example of the visualized flow pattern of bubbles; the white spherical spots represent the air bubbles. The mean bubble size db was measured from the visualized flow pattern by using image processing software. The flow pattern was visualized by laser light sheet (laser light source; Ar, 3W), and its photograph was taken by a high-speed video camera (Nikon, D70kit). Parameter db is calculated as an equivalent-diameter circle using the total area of bubbles in the photograph and the number of bubbles. When the bubbles were overlapped in the photograph, db is obtained as the value of the maximum and minimum diameter of the bubble, measured using a ruler. The db values upstream of the orifice with CR = 0.36 at y/D = −3.75 ~ −2.5 for α = 2.5%, 5.0%, and 10.0% at Re = 1.0 × 104 were 2.37, 2.23, and 2.78 mm, respectively, and those downstream at y/d =
![]()
Figure 9. Wall thinning rate TR and pressure fluctuation p’.
![]()
Figure 10. Pressure fluctuation p’ of Std and Std-Dp [11] .
![]()
Figure 12. Visualized flow pattern of Std (CR = 0.36, Re = 1.0 × 104).
2.0 ~ 12.5 were 2.6, 2.9, and 2.8 mm, respectively. Here, α [= Qa/(Qa + Qw)] is the volumetric flow-rate ratio of air to mixture flow, i.e., the apparent void fraction. In all cases, the bubble size appears smaller after the passing of the bubble through the orifice, because of shearing force generated by the orifice. The bubble diameter decreased with increasing Re; for example, at Re = 5.0 × 104, the above-mentioned bubble diameters of 2.6, 2.9, and 2.8 mm decreased to 2.27, 2.31, and 2.5 mm, respectively.
3.2.2. Flow Resistance
The flow resistance, i.e., p1 − p2, for the two-phase air-water flow was measured in a manner similar to that for the single-phase water flow, and the pressure loss coefficient Cp = 2(p1 − p2)/(ρum2) was obtained. The Cp values of the Std orifice for α = 0%, 2.5%, 5.0%, and 10.0% were 9.9, 10.0, 10.1, and 10.3, respectively, whereas, those of the Std-Dp orifice with Dp = 38.2 mm were 8.1, 8.7, 8.9, and 9.1, respectively. The Cp values of the Std-Dp orifice with Dp = 38.2 mm for α = 0.0 and 10.0% were about 6.1% and 2.0% lower, respectively, than those of the Std orifice.
3.2.3. Pressure Fluctuation
Shakouchi et al. [11] [15] showed that the wall thinning rate for a single-phase water flow can be expressed by the pressure fluctuation on the pipe wall downstream of the orifice. The pressure fluctuation exerts repeated variable force on the pipe wall, and as a result the pressure fluctuation p’ on the pipe wall, which is one of the major parameters governing the FAC for a single-phase water flow, is also considered to be the governing parameter for the FAC for a two-phase air-water flow.
An example of pressure fluctuation p’ for the two-phase air-water flow with CR = 0.36 and the Std-Dp orifice with Dp = 38.8 mm is shown in Figure 13. The TR value can be approximated using the p’ value and the relation shown in Figure 9. The p’ value for the two-phase air-water flow is larger than that for the single-phase water flow because of the collision of bubbles with each other and with the wall. The maximum p’ value, ![]() , for the two-phase air-water flow is attained at the apparent void fraction α of 10% and is about 28% higher than that of the single-phase water flow.
, for the two-phase air-water flow is attained at the apparent void fraction α of 10% and is about 28% higher than that of the single-phase water flow.
Figure 14 shows the relation between the maximum value ![]() and α. The
and α. The ![]() value of the Std-rev orifice is much smaller than that of the Std orifice. The
value of the Std-rev orifice is much smaller than that of the Std orifice. The ![]() value of the Std and Std-Dp orifices increase rapidly with increasing α until α = 2.5%, after which they attain a maximum value.
value of the Std and Std-Dp orifices increase rapidly with increasing α until α = 2.5%, after which they attain a maximum value.
The relation between ![]() and the pipe diameter Dp downstream of the orifice is shown in Figure 15. The
and the pipe diameter Dp downstream of the orifice is shown in Figure 15. The ![]() value is minimum at Dp = 38.8 mm regardless of α, and this minimum is approximately 10%, 9%, and 7% lower than those for α = 2.5, 5.0, and 10.0%, respectively, for the Std orifice. This means that the Std-Dp orifice can decrease the pressure fluctuation or pipe wall thinning caused by FAC downstream of the orifice.
value is minimum at Dp = 38.8 mm regardless of α, and this minimum is approximately 10%, 9%, and 7% lower than those for α = 2.5, 5.0, and 10.0%, respectively, for the Std orifice. This means that the Std-Dp orifice can decrease the pressure fluctuation or pipe wall thinning caused by FAC downstream of the orifice.
![]()
Figure 13. Pressure fluctuation p’ of Std-Dp = 38.8 mm (CR = 0.36, Re = 5 × 104).
![]()
Figure 14. Maximum pressure fluctuation p’max of Std and Std-Dp vs. α (CR = 0.36, Re = 5 × 104).
![]()
Figure 15. Maximum pressure fluctuation p’max of Std and Std-Dp vs. Dp (CR = 0.36, Re = 5 × 104).
4. Conclusions
Some of the authors [11] [15] have already reported that for a single-phase water flow one of the major parameters governing the FAC occurring on the pipe wall downstream of the orifice is pressure fluctuation p’. They have also indicated that the wall thinning rate TR can be estimated using p’, and that increasing p’ results in an increase in TR. This means that if p’ can be decreased, TR will also decrease.
In the present study, the flow-accelerated corrosion (FAC) on a pipe wall downstream of an orifice is examined phenomenologically. In particular, FAC of a two-phase, air-water bubble flow is studied and compared experimentally with that of a single-phase water flow. The main results are presented as follows:
1) For single-phase, water flow:
a) The pressure on the pipe wall downstream of the orifice fluctuates with time. For example, for CR = 0.36 and Re = 5.0× 104, the dominant frequency was measured to be approximately 5 Hz, and the maximum amplitude was observed at y/D = 2.0.
b) Using a smaller pipe diameter downstream of the orifice would decrease p’ while also maintaining the functionality of the orifice. Consequently, pipe wall thinning rate due to FAC can also be decreased while maintaining the functionality of the orifice.
2) For two-phase, air-water bubble flow:
a) As stated above, for a single-phase, water flow TR can be expressed using the p’ on the pipe wall downstream of the orifice. Pressure fluctuation p’ exerts repeated variable force on the pipe wall, it can also be considered as one of the major parameters governing the FAC for a two-phase, air-water flow as for a single-phase, water flow. The pressure fluctuation on the pipe wall downstream of the orifice for a two-phase, air-water bubble flow was clarified, and the estimation of the pipe wall thinning rate TR using p’ was presented as in the case of a single-phase water flow.
b) Using a pipe with a smaller inner diameter downstream of the orifice for a two-phase, air-water bubble flow would decrease pressure fluctuation. Consequently, pipe wall thinning rate due to FAC for a two-phase, air-water bubble flow can be decreased.
Acknowledgements
The authors would like to extend their gratitude to Chubu Electric Power Co., Inc., Japan who has provided a financial support for a part of this research.
Nomenclature
A0 cross sectional area of orifice
CR area contraction ratio of orifice
C flow rate coefficient
D, d pipe and orifice diameter, respectively
Dp pipe diameter downstream of orifice
k turbulent kinetic energy
p1 − p2 pressure loss at orifice
p, p’ mean and fluctuating pressure, respectively
Q volumetric flow rate
Re Reynolds number (=umD/ν)
TR wall thinning grate
um mean velocity of water flow in a pipe
ux’, uy’ turbulence component in x and y direction, respectively
x, y coordinate of radius and longitudinal direction, respectively
α volumetric flow rate ratio of air to mixture flow, apparent void fraction [= Qa/(Qa + Qw)]
ρ density of water
Subscript
a air
w water
NOTES
![]()
*Corresponding author.