Accelerated Testing of Devices on Durability and Fatigue Failure ()
Received 8 March 2016; accepted 7 May 2016; published 10 May 2016

1. Introduction
The problem of forced testing on reliability, i.e. the problem of construction of probability models for forced testing is formulated as an interposition of a distribution function 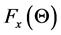 of time of failure-free operation of a device under load X on a distribution function
of time of failure-free operation of a device under load X on a distribution function 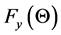 of the same quantity in the conditions of forced load
of the same quantity in the conditions of forced load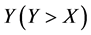 . The principle of forcing is that for random value
. The principle of forcing is that for random value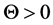 , we have inequality
, we have inequality 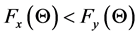 and functions
and functions 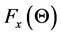 and
and  satisfy the following conditions:
satisfy the following conditions:
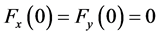 ,
,
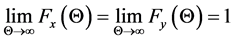 .
.
In the particular case of forced testing, we are concerned in finding certain quantitative properties of the distribution 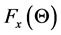 according to known properties of the distribution
according to known properties of the distribution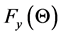 .
.
The problem of forced testing is reduced to definition of so-called “acceleration function” 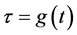 that represents the function of regression, i.e. correlation of quantiles (fractiles)
that represents the function of regression, i.e. correlation of quantiles (fractiles)  and t that correspond to equal probabilities
and t that correspond to equal probabilities  and
and 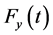 of failure-free operation in the face of nominal X and forced Y loads correspondingly. In general, this correlation is non-linear:
of failure-free operation in the face of nominal X and forced Y loads correspondingly. In general, this correlation is non-linear:
![]() .
.
The correlation of quantitative properties (moments) and the corresponding distributions ![]() and
and ![]() is easily determined from the following equations:
is easily determined from the following equations:
![]()
where ![]() and
and ![]() are initial and central moments of order k of distributions
are initial and central moments of order k of distributions ![]() and
and![]() .
.
In the case of linear model, when![]() , the problem is reduced to determination of sole coefficient c that depends only on the rules of distribution of failure-free operation of device with loads X and Y.
, the problem is reduced to determination of sole coefficient c that depends only on the rules of distribution of failure-free operation of device with loads X and Y.
2. Linear Theory of Forced Testing
2.1. Physical Principle of Reliability
When acceleration function is linear, it is enough to offer a technique of deterministic, forced testing that gives estimation ![]() of coefficient c, as well as lower
of coefficient c, as well as lower ![]() and upper
and upper ![]() boundaries of a sphere, where lies the true value of magnitude c with confidence level
boundaries of a sphere, where lies the true value of magnitude c with confidence level![]() .
.
It is more important that on the basis of acceleration function g, mathematical notation of so-called physical principle of reliability [1] gets absolutely new form. This hypothesis belongs to N.M. Sediakin:
![]() (1)
(1)
where ![]() signifies the distribution function of time of failure-free operation of a device, when set of these devices are initially tested with nominal load X during certain interval
signifies the distribution function of time of failure-free operation of a device, when set of these devices are initially tested with nominal load X during certain interval ![]() and then tested with forced load Y, when the same probability of failure is reached in lesser interval
and then tested with forced load Y, when the same probability of failure is reached in lesser interval![]() . Correlations
. Correlations ![]() and
and ![]() are functions of distribution of time of failure-free operation of a device in modes X and Y correspondingly.
are functions of distribution of time of failure-free operation of a device in modes X and Y correspondingly.
It is quite interesting to determine the criterions of linearity of acceleration function, because the problem of forced testing is essentially simplified for linear model. These criterions are formulated in the following form [2] .
Let us assume that one of the two sets are tested with load X during interval ![]() and then―with load
and then―with load ![]() during interval
during interval![]() . At the moment
. At the moment![]() , when testing is finished, probability of failure is
, when testing is finished, probability of failure is![]() . The second set of the same devices are initially tested with load Y during interval
. The second set of the same devices are initially tested with load Y during interval ![]() and then―with load X during interval
and then―with load X during interval![]() . At the moment
. At the moment![]() , when testing is finished, probability of failure is
, when testing is finished, probability of failure is![]() . Let us also assume that hypothesis of N.M. Sediakin is correct, i.e. physical principle of reliability is in force. In this case acceleration function g is linear, if
. Let us also assume that hypothesis of N.M. Sediakin is correct, i.e. physical principle of reliability is in force. In this case acceleration function g is linear, if ![]() and vice versa, i.e. if acceleration function is linear, then probabilities
and vice versa, i.e. if acceleration function is linear, then probabilities ![]() and
and ![]() are equal.
are equal.
2.2. Linear Summation of Failures
The physical principle of reliability in the form of (1) is essentially used for proving the above-mentioned theorem. Therefore, this theorem is realized only in those conditions, when hypothesis of N.M. Sediakin is correct.
We strictly prove [3] that when acceleration function is linear, physical principle of reliability is a sufficient condition for validity of so-called correlation of linear summation of failures which is also known as the rule of Palmgren-Miner:
![]() .
.
Figure 1 describes the meanings of magnitudes of this equation.
A.G. Palmgren [4] studied durability of bearings and offered above-mentioned equation in 1924 as a hypothesis. M.A. Minerused the same equation in 1945 in his studies [5] .
If we change the test a little bit and test the set of devices under load Y not during fixed time interval![]() , but until the moment of failure, then the last equation should be transformed. Particularly,
, but until the moment of failure, then the last equation should be transformed. Particularly, ![]() should be replaced with mathematical expectation
should be replaced with mathematical expectation ![]() of time, when the sample is tested under load Y until the moment of failure, if before that it was under load X during interval
of time, when the sample is tested under load Y until the moment of failure, if before that it was under load X during interval![]() . Similarly, quantity
. Similarly, quantity ![]() should be replaced with mathematical expectation
should be replaced with mathematical expectation ![]() of time of failure-free operation of device in normal mode X. Finally,
of time of failure-free operation of device in normal mode X. Finally, ![]() should be replaced with mathematical expectation
should be replaced with mathematical expectation ![]() of time of failure-free operation of device in forced mode Y. As a result, we get:
of time of failure-free operation of device in forced mode Y. As a result, we get:
![]() .
.
This equation represents the basic correlation for definitive, forced testing with technique of so-called “destruction” [6] . It is proved [7] [8] that random magnitude ![]() of resource of reliability
of resource of reliability
![]() ,
,
That is spent by device in random time ![]() of failure-free operation under any permanent load and intensity
of failure-free operation under any permanent load and intensity ![]() of failure, has exponential distribution and its mathematical expectation equals to 1, i.e.
of failure, has exponential distribution and its mathematical expectation equals to 1, i.e.
![]() . (2)
. (2)
This statement is true at any rule of distribution of random magnitude ![]() of time of failure-free operation of device.
of time of failure-free operation of device.
In the model of stepwise load that is shown in Figure 2, it is implied that load H is measured in discrete steps after time intervals ![]() and gets value
and gets value![]() . Index n is assigned to load, when there is failure. It is easy to see that
. Index n is assigned to load, when there is failure. It is easy to see that
![]() ,
,
where index n, as well as![]() , have random values.
, have random values.
Average time of failure-free operation of device in normal conditions (under nominal load) is denoted with symbol![]() . Symbol
. Symbol ![]() is used for average time of failure-free operation in mode
is used for average time of failure-free operation in mode ![]() under stepwise load and symbol
under stepwise load and symbol ![]() is used for the same value under permanent load
is used for the same value under permanent load ![]() in time x.
in time x.
If we assume that in every described mode, time of failure-free operation of element has exponential distribution, then the following equations are true:
![]() . (3)
. (3)
If we use property of additivity of resource of reliability and Equation (2) for the described two examples, then:
![]()
Figure 1. Graphical interpretation of palmgren-miner hypothesis.
![]()
These equations represent mathematical notations of correlation of linear summation of failures in discrete and permanent modes.
2.3. Models of Reliability for Certain Types of Load
We can describe considerable amount of reliability models for stepwise and permanent load, if we use mathematical notations of correlations of linear summation of failures that are based on the property of reliability resource.
For example, the following model is known:
![]() , (4)
, (4)
where m is a certain constant. Many researchers have got the same result. For example, for ball bearings ![]() [9] , for paper capacitors
[9] , for paper capacitors ![]() [10] [11] , for filaments
[10] [11] , for filaments ![]() [12] .
[12] .
For stepwise load, this model gives:
![]() .
.
If load is permanent and load H varies in time x with constant “rate” v on the basis of linear rule![]() , where
, where ![]() is initial value of load, then for average time
is initial value of load, then for average time ![]() of failure-free operation, we get:
of failure-free operation, we get:
![]() .
.
According to the work [13] , the following model satisfactorily describes the durability of many soft metals:
![]() ,
,
where E and m are certain constants.
For stepwise model and above-mentioned model, we get:
![]() .
.
When load increases permanently with constant “rate” ν and failure is observed at the random moment![]() , for the average value (mathematical expectation) we get:
, for the average value (mathematical expectation) we get:
![]() .
.
It is easy to see that the Equation (4) with assumption (3) and linear increasing load with initial value![]() , takes the following form:
, takes the following form:
![]() ,
,
Hence
![]() .
.
On the basis of previous equation we conclude that in the case of described conditions, random value ![]() of time of failure-free operation of device is distributed according to Weibul’s law:
of time of failure-free operation of device is distributed according to Weibul’s law:
![]() .
.
The specifications of form and scale of this law is described with the following equations correspondingly: ![]() and
and![]() .
.
These conclusions are based on a fact that if random value of time of failure-free operation of certain device is distributed according to Weibul’s law, then intensity of failure of this device is described with the equation![]() .
.
The result is important, because value m can be determined with the same statistical data that is given from the experiment with permanent load of the basic set of devices. It is sufficient to create the function of distribution of random value ![]() upon its N realizations
upon its N realizations![]() .
.
3. Conclusions
The problems of accelerated testing on durability are formulated newly, the basic definitions are given and the concept of so-called acceleration function is introduced. In the case of linear model, integral function of distribution of time of failure-free operation of a device is determined on the basis of this concept. The criterions of linearity of acceleration function are formulated and the techniques of accelerated testing are developed on the basis of correlation that generalizes the principle of Palmgren-Miner. This technique guarantees computation of reliability, when load increases permanently or stepwise.
Described method is easily generalized to the case of chemical engineering kinetics and chemical rate phenomenon.
Acknowledgements
We would like to express our very great appreciation to Dr. David Gorgidze for his valuable and constructive suggestions during the planning and development of this research work. His willingness to give his time so generously has been very much appreciated.
We would also like to thank the staff of the Strength of materials Laboratory at the Georgian Technical University for enabling us to visit their offices to observe their daily operations.
NOTES
![]()
*Corresponding author.