Thermodynamics of Criticality: Percolation Loci, Mesophases and a Critical Dividing Line in Binary-Liquid and Liquid-Gas Equilibria ()
Received 25 February 2016; accepted 26 April 2016; published 29 April 2016
1. Introduction
Almost 40 years ago, in their classic review on the status of liquid state theory [1] , Barker and Henderson began with the words “Liquids exist in a relatively small part of the enormous range of temperatures and pressures existing in the universe”. The tiny liquid area, in the T-p projection of Gibbs density surface, was defined within either a critical isotherm, or isobar, and a triple point. Above a critical temperature (or pressure) and below the triple-point, the liquid state did not exist. Not everyone agreed with these ad hoc bounds, however. For example, recent research on percolation transition loci on Gibbs thermodynamic surfaces [2] shows that J. D. Bernal may have been closer to the truth. Besides noting that the liquid state, albeit metastable, should extend down to absolute zero using random close packing as a starting point, Bernal also argued that the liquid state should extend to supercritical temperatures and pressures, where it is bounded from the gas phase by a “hypercritical” line of discontinuity.
Here, we report results for ideal gas properties, which, alongside real experimental p-V-T properties of a typical real fluid (argon), comprise compelling evidence that the liquid state is not bounded, by either the critical isotherm or isobar. Liquid and gas phases are terminated by percolation loci along any isotherm. Moreover, we find that percolation loci extend all the way from critical coexistence to low density states with ideal gas properties.
The equation-of-state of a real gas with finite molecular size (diameter σ) behaving ideally within a low-den- sity limit, is simply
(1)
where p* is a molecular-reduced pressure (pσ3/kBT), T is temperature (K), kB is Boltzmann’s constant, ρ* is a reduced density (ρ* = Nσd/Ld), where Ld is length (L, d = 1), area (A, d = 2) or volume (V, d = 3). Equation (1) has an abiding role in the description of thermodynamic properties of real molecular fluids. Pressure is everywhere continuous; second and all higher derivatives of p(ρ) are zero. Because of this simplicity, all state functions are exactly known for any d. Equation (1) is a universal scaling law that spans the dimensions.
Within the ideal gas limit of obedience to Equation (1), real fluids with finite size, i.e. σ > 0, however, exhibit various properties that cannot scale with d, linear transport coefficients, for example. Percolation transitions, not unrelated to the transport coefficients, are also strongly dimension dependent in form, and are known to determine thermodynamic phase changes in model lattice gases [3] . Percolation transitions of the available volume (VA) and excluded volume (VE) for the insertion of one more molecule of a finite diameter are properties relating to Gibbs energies that effect phase transitions.
For hard-core fluids,
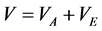(2)
then, the ensemble averages 
and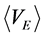 
equate with chemical potential (μi) of species i
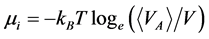(3)
Equation (3), with Equation (2), defines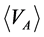 
and 
for real fluids.
For the ideal gas, percolation of VE is defined as a density above, or temperature below which, the overlapping exclusion spheres of radius σ/2 from a point in a uniformly random distribution of N points, form clusters that can span the whole of V. VA comprises a distribution in configuration space of accessible pockets in which there are no ideal gas point molecules within one sphere diameter anywhere in the pocket. The percolation transition for VA is the density above, or temperature below which, the empty pockets coalesce to span the system. For temperatures above percolation, VA comprises a network of connecting pathways to the whole system accessible to a diffusing sphere in the static ideal gas equilibrium configuration.
2. Percolation Transitions
For an ideal gas the exclusion sphere diameter defines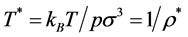
. Experimental coexistence data on binary liquid phase diagrams is generally obtained at constant pressure (1 atm.) and presented with temperature (T) the dependent variable as a function of mole fraction (XB), hence at this stage, with binary liquids in mind, we choose T* as the state variable. (note: for an ideal gas
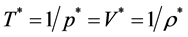) We designate the percolation transition reduced temperatures as 
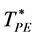and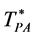 
respectively. Relationships between dimensionality and percolation transitions can be summarized:
d = 1 no percolation
d = 2 PE and PA coincide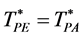 
and ![]()
d = 3 there is an inequality ![]()
and ![]()
There is a fundamental difference between 2 and 3 dimensions. For d = 2, there are two regions, “gas-like” ![]()
and “liquid-like”![]()
, whereas for d = 3 there are three regions, gas-like T* > TPA, liquid-like T* < TPA and a mesophase,![]()
. In the mesophase, both the pockets of availability and clusters of exclusion sites percolate the system. The mesophase is both gas-like and liquid-like.
PE both for d = 2 and 3 has been investigated by a number of authors for the present and related systems [4] - [11] Rough estimates of PE for d = 2 and 3 ideal gases can be gleaned from Figure 3 and Figure 4 of the paper by Bug et al. [4] . Extrapolating their data points, when their attraction parameter ε = 0, to zero density one obtains for d = 2 ΦPE ~ 1.2 and for d = 3 ΦPE ~ 0.35, where Φ is the excluded volume fraction (=πρσ3/6). Heyes and coworkers [5] - [8] report related investigations of PE for various models by MC and MD simulations. From an interpolation to zero density of the hard-sphere fluid variable-exclusion shell percolation threshold Heyes et al. [7] obtain ΦPE = 0.346 (d = 3). The most accurate values for both the d = 2 (PE and PA) percolation transition are probably those of Ziff and coworkers: the values for ρ* are 1.275 (d = 2) and 0.653 (d = 3). An extensive study of ideal-gas PE transitions for exclusion squares, cubes, and other geometric shapes has also been reported [11] .
Educational insight, and estimates of ![]()
for d = 2 can easily be obtained pictorially in just a few minutes using an EXCEL spreadsheet. Figure 1 shows a typical configuration, 2000 random numbers from a uniform distribution 0 - 1, i.e. an ideal gas (N = 1000) in the vicinity of the percolation transition. Disc diameters do not vary when the square area is expanded or contracted on the display. Fixing the diameter at 5 mm, percolation
occurs at L ~ 14.0 cm hence ![]()
or![]()
, i.e. in close proximity to reference [9] . Computation of PA for the ideal gas d = 3 has not previously been reported.
There are no reports of PA (d = 3) having been previously investigated or determined for the ideal gas, although the transition density ![]()
is known to be 0.537 ± 0.05 for the hard-sphere fluid [12] . Here, we use the same methods, and criteria for percolation, as described previously for the hard-sphere fluid. Both ![]()
and ![]()
have been computed for a range of finite size systems; the results are summarized in Figure 2. Thermodynamic limiting values (N à ∞) are obtained from the linear trendlines.
Every configuration either has a percolating cluster or it does not. Clearly, for small finite systems, there will be configurations that percolate, and some that do not, in the vicinity of PE. The percolation threshold in the computations of Heyes et al. [5] - [8] was defined when 50% of configurations have a percolating cluster, with details described by Seaton et al. [13] . Here, we define PE using an ensemble average definition of a percolation
![]()
![]()
![]()
(a) (b) (c)
Figure 1. Excluded and accessible areas (black and white respectively) for a configuration of a two-dimensional ideal gas: (a) “gas-like” density below the percolation transition (b) close to the percolation transition and (c) “liquid-like” density above the percolation transition.
![]()
(a) (b)
Figure 2. (a) Ideal gas PE transition (![]()
) from the mean cluster size distribution saddle-point method [12] for a range of finite systems: (b) Ideal gas PA transition (![]()
) from zero-diffusivity limit method [12] .
density [12] ; i.e. ![]()
is the saddle-point density above which the cluster size probability distribution P(n) is bimodal. This is the normalized probability of a site belonging to a cluster of size n. Above![]()
, P(n) is a monotonic gas-like distribution, for all PE below ![]()
it is bimodal. Plotting the saddle-point definition of ![]()
against 1/N1/3 (Figure 2(a)) gives a linear trendline that interpolates to the result ![]()
(![]()
).
Our method for determining ![]()
is essentially that described previously for hard spheres [12] , except that it is easier for the ideal gas. Here we use N-V-T MD for non-additive binary spheres that can simulate the Widom- Rowlinson (W-R) model fluid [14] [15] . This belongs to the general class of symmetric binary non-additive hard-sphere fluid mixtures defined by collision diameters
![]()
where δ is a dimensionless non-additivity, that varies from −1, for the W-R penetrable-sphere model binary fluid, via zero for one-component hard spheres, to infinity. Positive δ relates to ionic liquids and ionic crystal structures when mole fraction XB = 0.5.
The MD program solves equations of motion of a binary mixture NA + NB. The results for the PA values in Figure 2(b) are obtained by the mean-squared displacements of B average over many frozen random configurations of ideal gas A. As the B particles do not interact with themselves, we average over all NB in the same MD simulation run. All the values in Figure 2(b) were obtained for equimolar systems. Plotting the point of zero dif-
fusivity, Di(ρ, N) à 0, against N (NA in MD run) gives a linear trendline with the result ![]()
(![]()
).
3. W-R Model Binary Liquid
3.1. MD Simulation Results
We have determined ![]()
along isopleths of the binary W-R model fluid; T* is defined as T* = 1/p* and p* = pσ3/kBT. MD simulations have some advantages over Grand Canonical Monte Carlo [15] (GCMC). Not least is the direct extraction of transport properties for determination of ![]()
loci. These are obtainable by “freezing” component A whilst allowing B to diffuse. The cluster distributions that determine ![]()
also yield accurate values for coexisting XB by integrating the solute cluster probability distribution P(n) which decreases monotonically, from a maximum at n = 1, to zero for clusters of B in solution of A, or vice-verser. Accurate MD pressures are calculated from A-B collision frequencies.
What is the effect on the percolation transitions of increasing the mole fraction of B from the ideal gas limit (XB = 0)? For the isopleth at XB = 0.1, and for N = 10,000, the reduced pressures at which the two transitions occur, i.e. ![]()
and ![]()
are 0.715 and 0.923 respectively. We find, up to XB = 0.1 and beyond, both percolation pressures increase with XB, PE more so than PA, roughly according to
![]()
![]()
where![]()
. The percolation transition pressures increase with ![]()
because, as B are added at constant T, the system expands with both VA and VE increasing, but VE increases more than VA; adding B causes A-sites to cluster more, whilst creating more spherical B-pockets. The pressures of percolation transitions for finite XB appear to be coincident with higher-order discontinuities (Figure 3) in the supercritical region. Weak thermodynamic discontinuities have been both predicted theoretically for real systems [16] , and reportedly seen experimentally [17] . Changes in pressure slopes are evident from the MD excess pressures defined relative to the ideal gas.
![]()
(4)
Figure 3(a) shows the isopleth XB = 0.1 has four distinct regions. At high density, in the two-phase region, the MD pressures averaged over 100 million A-B collisions still show fairly large uncertainties. The maximum pressure along any isopleth coincides with the first-order mixing-demixing transition. This reflects the thermo-
dynamic equilibrium condition of minimal Gibbs energy (G) (since![]()
) for equilibrium on either side
of the transition. At the mole fraction XB = 0.1 in the mesophase region pressure increases linearly with density. In the one-phase region, the MD data is sufficient to observe that the percolation loci appear to be associated
![]()
(a)![]()
(b)
Figure 3. Excess pressures of the Widom-Rowlinson binary fluid mixture: (a) along the isopleth XB = 0.1 (N = 10,000); (b) along the equimolarisopleth XB = 0.5 (N = 8000).
with changes in slope that could reflect higher-order thermodynamic phase transitions, but presently not sufficiently accurate to establish the order or strength of discontinuities.
The vertical dashed lines in Figure 3 correspond to the percolation transition densities computed explicitly by the methods described in the text and referenced [5] : they coincide with changes in the slope of the excess pressure. The MD results for XB = 0.5 show three regions; there is no PA, just the PE transition at the density 0.65. The change in the slope of![]()
, and hence also p*, is more pronounced. The rigidity function (dp/dρ)T is again constant in the mesophase, close to zero as evidenced by a very slight slope.
3.2. Demixing Phase Transition
In all previous investigations of the W-R fluid, the existence of a critical point singularity at the UCST has invariable been assumed at the outset [14] [15] . The connection between percolation loci and phase transitions is now well-established. Equation (3) of this paper exactly relates VA or VE to chemical potentials, which determine equilibrium between phases. The essential new result here, is for the percolation of VA i.e. ![]()
in 3d (Figure 2(b)) which ~35% greater than the already known![]()
. Between these transition temperatures both VE and VA percolate, hence the mesophase only exists in real 3d liquid-liquid or liquid gas fluids. This result for the ideal gas enables the connection between percolation loci and the demixing transition to be determined.
As solute concentration (XB) increases in the W-R fluid, the two percolation temperatures become closer and then coincide. From thermodynamic considerations, this intersection triggers a first-order phase transition, with the two different phases having the same T, p and chemical potential. It is this fundamental property of percolation in 3d that does not exist in 2d that vitiates the hypothetical concept of universality, and confirms the new science of criticality for both liquid-gas [2] , and now also liquid-liquid coexistence.
Along any isopleth, the pressure is a maximum at the two-phase boundary to comply with the thermodynamic requirement of minimum Gibbs energy as shown in Figure 3. However, we have also determined the coexistence line directly from the results for the XB = 0.5 equimolar isopleth by a more accurate method than GEMC [15] , by integrating the cluster distribution, obtained from all MD runs, up to the hiatus in 2-phase region. Figure 4 shows some plots of the cluster distributions and the integrated mole fractions. The distribution is bimodal in the mesophase and monomodal in the one-phase region. In the two-phase region it is bimodal with a hiatus.
Reference [15] provides an estimate of the coexistence density and pressure for several XB well away from the critical coexisting compositions. For XB = 0.1, ρ* ~ 0.86. Because of the symmetry of the W-R model the mean of the two coexisting compositions at the upper critical consolute composition must be at XB = 0.5. Our results show that there is no “critical point”. Thus in Figure 3(b) the onset of the two-phase region is at the mean criti-
![]()
(a) (b)
Figure 4. (a) Cluster size distributions for W-R binary fluid; (b) integrated mole fractions for state points in 4a showing how the coexistence mole fraction is obtained in the 2-phase region, e.g. at the density 0.8 (black points) XA = 0.214 ± 0.01.
cal density; there is a flattish pressure vs. density mesophase up to the phase separation followed at higher densities by a steady fall of pressure in the two-phase region. The vertical line is at ρ* ~ 0.75 is close to the previously estimated demixing density ρ*(T) = 0.749 of de Miguel et al. [15] .
The percolation loci on the T*-XB surface (Figure 5), to within the uncertainty of the data, decrease with XB an intersection occurs when T* = 1.00 ± 0.01 with the uncertainty estimated from the combined regressions. At this intersection the fluid phase separates as solutions of A in B and B in A have the same T, p, and μ of both species
(chemical potential). Solving for XB when ![]()
gives XB = 0.339 for the critical coexistence mole fraction.
From the coexistence pressures, and direct computations of PA and PE, we are able to construct a phase diagram for the W-R binary fluid. The temperature loci of the percolation transitions fit the trendlines (dashed lines in Figure 5)
![]()
![]()
showing the connection between percolation and the demixing phase transition. Note the perfect symmetry about the isopleth XB = 0.5.
The present results show a dividing line at![]()
, rather than an Ising-like singular critical point. The evidence for higher-order discontinuities at PE and PA loci may invalidate some mean-field theoretical approaches.
The W-R binary fluid is essentially a simple model of partially miscible liquids, e.g. cyclohexane and methanol. The high-density fluid states at low temperatures are immiscible ideal gases. Here we have an example of what could arguably be described as “liquid states” of the ideal gas. Within the respective uncertainties, the present results agree with de Miguel et al. [15] . Our phase diagram could just as easily be presented as p*, ρ* or V*, it would not change the science. We choose T* to identify directly with real binary-liquid experimental phase diagrams that exhibit a similar UCST (Figure 6).
3.3. Experimental Evidence
Many mixtures of dissimilar liquids, just as seen here for the W-R fluid, separate into two coexisting phases over a lower temperature range. On heating, compositions of the two phases become more and more similar and at a critical temperature there is a single phase. This is the UCST. At higher temperature there is just one liquid phase. It is possible to define various percolation thresholds for clusters of solute molecules in the single liquid phase by analogy with clusters of molecules in a gas phase. The present evidence suggest that they these percolation loci that delimit the solution will give rise to a mesophase and a coexistence line the UCST [17] .
![]()
Figure 5. Phase diagram of the Widom-Rowlinson binary fluid; ![]()
and ![]()
loci blue and green respectively; percolation transitions of the ideal gas open circles at XB = 0; computed 2-phase coexistence state points are the red circles.
![]()
Figure 6. Typical experimental data points for the 2-phase coexistence of a partially miscible liquid-liquid mixture showing a UCST at horizontal line within the uncertainty: data from [19] [19] The black dot is a hypothetical “critical point”.
Experimental critical parameters for a range of partially miscible binary liquids are tabulated in Kaye and Laby [19] . The critical compositions are actually mean compositions of the maximum observable coexisting compositions, defined and obtained using the law of rectilinear diameters in the vicinity of Tc., usually in conjunction with a cubic equation-of-state, or similar [19] [20] . This also applies to the critical densities of computer models using Gibbs ensemble Monte Carlo methods [15] , just as for liquid-gas coexistence in square-well model fluids [21] - [24] . Likewise, within the uncertainties of experimental measurements of liquid-liquid UCST (Figure 6), the coexistence envelopes at Tc are flat on top. The hypothetical “critical point” has been obtained using a priori hypothesis of existence, and is defined only by a numerical parameterization.
The simulation results we present for the W-R mixture suggest that the phase diagram of real liquids will be determined by the intersection of percolation loci. These results for the W-R mixture should stimulate further laboratory experimental research into the percolation loci. The critical “point” in Figure 6 is defined only by a numerical parameterization using a theoretical functional form that presumes its existence.
4. PCS Liquid-Gas Model
Probably the simplest 3D model Hamiltonian of a molecular fluid, which is continuous in phase space, and exhibits liquid-gas criticality and two-phase gas-liquid coexistence, is the penetrable cohesive sphere (PCS) fluid [14] [15] . The internal energy (U) is simply
![]()
(5)
where kB is Boltzmann’s constant and T is temperature (K); the angular brackets denote a configurational average. Equation (5) defines an attractive molecular energy (ε) complementary to the volume of overlapping clusters, i.e. VE as defined above for an ideal gas, of a configuration of N penetrable spheres, and ν0 (=4πσ3/3) is the volume of a sphere. At low temperatures, this model exhibits the exact properties of an ideal gas in both the low- density (gas phase) and high-density (liquid-phase) limits. Here again, there is a liquid-like state with the properties of the ideal gas. Both W-R and PCS models, therefore raise a curious conundrum. Could a supercritical fluid with the properties of an ideal gas be described as “liquid”?
Experimental thermodynamic liquid-gas coexistence phase diagrams [21] [23] have traditionally been obtained along isotherms by measurements of coexistence pressures. Hence, we prefer to maintain the connection with experimental data of gas-liquid thermodynamic equilibrium measurements established over a period of 150 years by plotting p(ρ)T isotherms (note the contrast with [15] ). A more detailed analysis of the connection of percolation loci with experimental isotherms is recently published [18] .
Every state of the PCS fluid corresponds to a transcribed state of the W-R binary model fluid. The equations for the transcription from the W-R binary percolation and coexistence pressures (Figure 7(a)) to the PCS one-component gas-liquid pressure can be derived, for example, from an analysis of the respective grand partition functions as described by de Miguel et al. [15] . The transcription equations we need here are
![]()
(a) (b)
Figure 7. (a) Phase diagram of the W-R binary fluid in the pressure-density projection: ![]()
and ![]()
loci are dashed blue and green respectively; coexistence data points are red circles; (b) phase diagram of the PCS liquid-gas system obtained by transcription of W-R pressures in 7a.
pressure ![]()
(6)
density ![]()
(7)
where ![]()
is the thermodynamic activity of a component defined as lnZ* = μ/kBT and μ is Gibbs chemical po-
tential relative to the ideal gas at the same T, p. Gibbs energy change, hence Z*, can be obtained by integrating the excess pressure loci at constant T, with respect to density.
![]()
(8)
For the one-component isomorphism of W-R fluid, pressure is the natural variable so the p* vs. ρ* representation along isotherms relates directly to experimental results and phase diagrams. We plot the values of the pressure at coexistence vs. ρ* which we plot in Figure 7(b). Itshows that the simplest imaginable continuous Hamiltonian model to exhibit liquid-gas coexistence and a critical temperature has a coexistence line at the intersection percolation loci as observed for square-well and Lennard-Jones model fluids and many real fluids [24] - [28] . There is a liquid-gas critical dividing line between 2-phase coexistence and a supercritical mesophase. The liquid state extends to an ideal gas zero density and pressure limit. This raises the question: could there exist a high temperature limit of the percolation transition loci in real fluids at very low density in the region of obedience to the ideal gas law?
The evidence suggests this is indeed the case, provided we re-interpret the experimental thermodynamic properties of real fluids in the light of our knowledge of percolation transitions. For 80 important gases or liquids, including the simplest real liquid argon, in the NIST “Thermophysical Properties of Fluid Systems” data bank [23] , equation-of-state p-V-T data with 6-figure accuracies are obtainable. These p(ρ)T supercritical isotherms have been formulated, however, using a large number of parameters and an assumption of a supercritical continuity of liquid and gas. If there were to be no continuity of liquid and gas, there would need to exist three different equations-of-state to describe the gas and liquid phases, bounded by percolation loci, and the mesophase region in between. Present findings suggest theory-based equations-of-state with far fewer parameters, and with scientifically correct functional forms should eventually replace the NIST equations. Present observations indicate a virial expansion for the gas phase, perhaps a free-volume expansion for the liquid, and a linear combination for the mesophase.
5. Real Fluids
Although lacking a molecular-level definition, for any real fluid, for which an exact Hamiltonian is generally unknown, the percolation loci can be defined and obtained phenomenologically along any thermodynamic equilibrium isotherm by the rigidity inequalities [18] . In the case of real fluids with attractive potentials, the percolation transition bounding the gas phase, i.e. the counterpart of PE for impenetrable spheres, has been designated PB, as it is a percolation of bonded clusters.
Rigidity (ωT) is the work required to isothermally increase the density of a fluid; with dimensions of molar energy and is plotted for a range of isotherms for CO2 in Figure 8. The symmetry of the rigidity in both the subcritical and supercritical regions is the subject of a recent paper [18] . We note from Figure 8 that the percolation loci PB and PA appear to be converging at the Boyle rigidity in the case of CO2.
The rigidity state function relates directly to the change in Gibbs energy (G) with density at constant T according to
![]()
(9)
The following inequalities (10)-(12) are presently empirical, but do have a molecular-level explanation in terms of the number density fluctuations of gas and liquid respectively [18]
gas ![]()
![]()
(10)
meso ![]()
![]()
(11)
liquid ![]()
![]()
(12)
It is clear from Equation (9) that ω > 0, i.e. rigidity must always be positive: Gibbs energy cannot decrease with pressure when T is constant. By these definitions, moreover, not only can there be no “continuity” of gas and liquid, but the gas and liquid states are fundamentally different in their thermodynamic description. Rigidity is determined by number density fluctuations at the molecular level, which have different density dependencies in either phase. The gas phase comprises one large void with many small clusters, which determine fluctuations, whereas the liquid phase comprises one large cluster and with many vacant pockets, which determine density fluctuations. Since the properties of a hole or an occupied site are statistically equivalent, this give rise to a symmetry of supercritical properties between gas and liquid phases [18] .
Experimental argon isotherms [21] - [23] from the critical temperature (Tc = 151K) to 500K are plotted in Figure 9. All the isotherms below a temperature around 400K show that there is a flat meso region, i.e. (dω/dρ)T = 0. In this narrow range, for each supercritical isotherm, to within the uncertainty of the original experimental data, the rigidity is constant. A value can be obtained by a linear fit over a finite density range with a linear trendline regression between 0.999999 and 1.0 for all the supercritical isotherms in Figure 9. An accurate equation- of-state for the meso region is thus obtained
![]()
(13)
![]()
Figure 8. Supercritical isotherms of carbon dioxide: the rigidity is obtained from NIST thermophysical tables with 4-figure accuracy [23] : loci of PB and PA that bound gas and liquid respectively are the dashed lines. The percolation loci appear to be converging at ρ = 0; the Boyle temperature for CO2 is 715K corresponding to a rigidity of 5.945 KJ/mol.
![]()
(a) (b)
Figure 9. Supercritical isotherms of fluid argon from NIST Thermophysical Property Tables [23] : loci of PB and PA are green and blue respectively (a) pressure isotherms; (b) rigidity isotherms.
where ωT is the rigidity along any isotherm T(K) and p0 is a pressure constant. The percolation loci densities can be estimated by observing the differences p(gas) − p(meso), and p(liquid)?p(meso), both decrease quadratically with density, and interpolate to zero at the percolation loci densities ρPB and ρPA.
The initial slope of the percolation loci in the pressure plot (Figure 9(a)) corresponds to an intercept temperature obtained from percolation loci in Figure 9(b) at zero density, as ω(ρ → 0) = NkBT for an ideal gas. All molecular gases exhibit a characteristic temperature at which the second virial coefficient changes sign. This corresponds to a low-density limit of the percolation transition loci that may converge together at or below this temperature. The Boyle temperature of argon is 407 K [23] corresponding to a rigidity of 3.38 KJ/mol.
6. What Defines “Liquid Phase”?
6.1. Phase Diagram
The results presented here for the percolation transition loci comparing both real and model fluids reaffirm previous observations [24] - [28] that there is no critical point singularity on Gibbs density surface for gas-liquid condensation. Rather, there is a coexistence boundary line at the critical temperature, above which there exists a mesohase between the percolation loci that bound the liquid and gas phases. From the present W-R results, we can further infer that partially miscible liquid-liquid mixtures will also show an upper critical consolute temperature with a dividing line separating one- and two-phase regions. Above this critical divide, there will be a mesophase bounded by the percolation loci that may extend to the ideal dilute solution limits. Experimental studies of liquid-liquid UCST phenomena, however, are limited, being generally at ambient pressures and terminate at the boiling temperatures.
Returning to the question about universality and dimensionality dependence of the description of criticality, we observe for d = 2, since PE = PA for all densities (or concentration XB), the phase behavior and criticality will be quite different; there can be no mesophase in 2-dimensions. We conjecture, therefore, that the percolation locus intersects the equimolarisopleth with a critical singularity at XB = 0.5 for the d = 2 W-R model. Another consequence of the absence of a d = 2 mesophase would be no metastability beyond the first-order phase boundaries, and, unlike d = 3, no metastability and hence no spinodals within the subcritical bimodals. The existence of a mesophase is a property only of d = 3 systems. This difference in the description of liquid-gas criticality between 2 and 3 dimensions vitiates the hypothetical “universality” concept as applied to liquid-gas, and binary-liquid, criticality.
The present results for various percolation loci suggest that all real atomic and molecular fluids will have a liquid state that is bounded only by a percolation transition at high temperature and its equilibrium freezing transition at low temperature along any isotherm. The boundary may be defined phenomenologically by inequality (12). The locus of this liquid-state boundary is seen to extend all the way from the liquid critical temperature and pressure, to an ideal gas at limiting low density. On the basis of these observations, it is the “gas phase”, i.e. defined by the inequality (10) that exists in a limited area of the universal T-p plane.
We note, however, that there can be no zero of density/pressure for a real fluid, as they become logarithmic to high vacuum levels. The truly ideal gas cannot exist in reality; the sign of the second virial coefficient determines the designation “gas” or “liquid”, by the rigidity criterion and in this limit. The liquid area of existence extends to infinite pressure and temperature; whereas the gas phase extends to infinite vacuum, but only below a certain temperature. It appears the liquid phase will extend upwards in temperature, for all pressures to perhaps continuously become plasma (Figure 10). This is contrary to what is hitherto generally believed to be liquid state [1] .
6.2. Ideal Gas Connection
The symmetry similarity between gas and liquid opens the way to an alternative definition of liquid state, which is usually regarded just as the high density portion of the fluid phase below the critical temperature, i.e. defined ad hoc as being bound by the critical isotherm, or sometimes the critical isobar. Here we advocate a thermodynamic definition. A “liquid” phase can be identified as the region at density higher than the available volume percolation transition.
On examination of the loci of two percolation transition densities in real gases at high dilution, we note that these lines do not have any thermodynamic signature in the equilibrium properties of the ideal gas. The “ideal gas” is a fictitious concept that cannot exist in reality. In any real gas, the density cannot go to zero. It is logarithmic; for all real gases behaving ideally, thermodynamic properties everywhere depend upon a distance scale. In the W-R binary-liquid and PCS fluid it is the penetrable sphere diameter. For real gases, the percolation transitions are present in the low-density region of obedience to the ideal gas law, i.e. when p ~ ρkT and extend to the Boyle temperature. Thus, in the low-density limit, the boundary between gas and “liquid” phases according the criteria of Equations (10)-(12) becomes the sign of the second virial coefficient (b2), as defined in the expansion of pressure in powers of density along any isotherm
![]()
(13)
In the gas region of the phase diagram b2(T) is negative, whereas in a region of a liquid phase it is positive; at the Boyle temperature b2 is zero.
A definition of liquid state based on the existence of percolation lines has implication for the thermodynamics of the system for the following reason. When the two supercritical percolation lines that bound the existence of liquid and gas phases intersect on the Gibbs density surface the respective phases have the same temperature and pressure but different densities, and therefore also the same Gibbs chemical potential, and hence coexist at a first-order phase transition. These new results for the percolation transitions of an ideal gas and loci for model fluids, are valuable contributions to the literature as they lead to an alternative more plausible interpretation of the phase behavior of the W-R model binary liquid and the one-component liquid gas fluid. The possible alternative operative description of “liquid” phase is a corollary of these findings.
![]()
Figure 10. Phase diagram for argon showing the percolation loci that bound the liquid and gas states and mesophase: the tiny shaded area is generally referred to as “liquid”: the red circle is the critical point on the p-T projection [1] .
7. Conclusions
In Section 2 we have presented a new result for the penetrable sphere available volume percolation transition temperature (![]()
) of an ideal gas and found that![]()
. We conclude that the d = 3 ideal gas has three
regions liquid-like, gas-like, and a meso-region wherein both VE and VA percolate. The connection to the coexistence envelope of a W-R fluid is the ultimate compelling evidence for the absence of any van der Waals singularity on the density surface of liquid-gas equilibrium or on composition surface of the partially miscible binary liquid at the critical temperature or pressure.
In Section 3 we have reported the direct determination of both percolation loci ![]()
and ![]()
along several
isopleths of the W-R fluid. We find that both percolation loci decrease with composition XB (or XA) and, around T* ~ 1, and intersect with two phases then having the same temperature, pressure and minimal chemical potential at the known critical temperature. It is wholly consistent with previous results for the intersection of percolation loci in the p-T plane at the critical temperatures for model square-well fluids [23] , Lennard-Jones fluids [24] , and real fluids including argon [26] [26] and water [27] . To suggest that percolation transitions are unrelated to thermodynamic properties would imply that the intersection of percolation loci at pc-Tc, in all these systems, would have to be a series of incredible coincidences. This is quite implausible.
The phase behavior (Section 4) for the model penetrable sphere fluid obtained by transcription of the W-R fluid properties, therefore, is further compelling evidence that there is no critical point on Gibbs density surface for liquid-gas equilibria. This simple model liquid-gas Hamiltonian shows a critical dividing line between a maximum coexisting gas density and a minimum coexisting liquid density, above which exists a supercritical mesophase.
We have also shown that the thermodynamic state function rigidity, (dp/dρ)T, can define a distinction between gas and liquid. For any one-phase system rigidity is everywhere positive; in any two-phase region ω = 0. Rigidity decreases with density for a gas and increases with density for a liquid. For temperatures above critical coexistence the rigidity has a constant value in the mesophase that separates the percolation loci, which bound the limits of existence of liquid and gas phases in the supercritical region.
We have compared the results for the ideal gas percolation ratios with the high-temperature, low pressure and density, limits of argon. The results from the modern NIST thermophysical property tables [23] indicate that the supercritical mesophase, at least in the case of simple fluids, extends all the way to a dilute gas behaving ideally. This reopens the debate “What is liquid?” [1] .
Finally, we have presented results that show there cannot be “universality” in the description of criticality between 2- and 3-dimensional systems. The mesophase is a fundamental property of complementary excluded and available volume percolation loci only in 3d, which does not exist in 2d. Hence, there can be a critical point singularity on the density surface of 2d fluids, whereas it is a critical dividing line for real 3d liquid-gas thermodynamic systems.
Acknowledgements
We acknowledge this paper is written by invitation of Guest-Editor Prof. Chan Kwong-Yu of the University of Hong Kong in honor of distinguished liquid-state physicist Dr. Yiping Tang. This version has benefited from some referees comments. We remain heartened, however, that there is nothing to vitiate this new science of criticality in any previous referee reports, including those contrived by Molecular Physics editor G. Jackson to reject this new science of liquid-gas criticality. These reviews and rebuttals, together with an acknowledged list of known contributors to this debate, will be published elsewhere. https://www.researchgate.net/profile/Leslie_Woodcock