An Extreme Value Analysis of Wind Speed over the European and Siberian Parts of Arctic Region ()
Received 11 January 2016; accepted 5 April 2016; published 8 April 2016

1. Introduction
This paper focuses on changes in extreme wind events in the Arctic region. For the purpose of ensuring the safety of infrastructure (particularly at exposed sites such as bridges, high buildings, wind turbines and radio masts), it is usually a requirement to estimate the extreme loads they might be subjected to during their service time. In the maritime sectors, the extremes of low-level winds can generate huge oceanic waves and storm surges that consequently may lead to the damage of marine structures (ships, drilling platforms) and coastal erosion. This is especially the case during the cold period in the Arctic, where regular events of intense wind velocities are typically observed. The quantitative analyses of spatial variation of extreme wind patterns are important for effective wild fire management and sustainable long-term urban development on fire-prone landscapes. It is therefore worthwhile to properly assess the distribution of wind extremes and their origin.
Research in the statistical analysis of extreme values has flourished over the past several decades: new probability models, inference and data analysis techniques have been introduced; and new application areas have been explored [1] - [3] .
Extreme value analysis of wind speeds (U) is generally performed through implementation of the following idea. Beginning with a parent distribution whose cumulative distribution function (cdf) is F(U), the distribution is sampled n times, and the maximum value of the n samples is obtained. This maximum value has a cumulative distribution function of its own of simply Fn(U). This relationship leads to the extreme value theory noted by Fisher and Tippett [4] that for sufficiently long sequences of independent and identically distributed random variables, the maxima of these sequences can be fit to one of three limiting distributions. This result has been quantitatively refined by Gnedenko [5] . One representative of these three limiting distributions is the Weibull distribution, which has traditionally been used for the statistical modelling of wind extremes (see [6] ).
In another approach, the Pareto distribution is applied to the peaks of independent storms that exceed a sufficiently high threshold (see [6] and [7] ).
Many studies of the estimation of extreme wind speeds are commonly expressed in terms of the quantile value U(p), or UT, the maximum wind speed (which is exceeded, on average, once every T years), and the return period (the corresponding return period is given by T = 1/(1 − p)). In this situation, the data are generally fitted to a theoretical distribution curve in order to calculate the quantiles. To insure the independency of the data, a certain minimum separation time is maintained among the data selected for the analysis.
Statistical method of the extreme value analysis of wind speeds is important because it allows us to detect their statistical model. Note, that the same statistical distribution suggests a common originating mechanism. We plan to use such idea to interpret of the extreme wind records.
A striking aspect of anticipated global climate change in response to increasing greenhouse gases is that the largest warming is predicted to occur in the Arctic. This observed warming has affected glaciers, sea ice, ecosys- tems, permafrost and the coastal geomorphology. It is likely that such warming affects meteorological regimes (e.g., extreme conditions). Because the climate models are the tools used to simulate climate change, it is very important to understand to what extent wind speed extremes can be reproduced by a general circulation atmospheric models within those climate models. The use of station data will make it possible to evaluate the consistency, in terms of reproduction of statistical behavior, between model simulation products and near-surface observations.
The next section reviews the study area and dataset. The following sections describe the evidence for Weibull distribution in station observation data and in model data as well. The last section concludes the paper.
2. Study Area, Dataset and the Question of Statistical Independence
The study was performed over the Arctic region from the Kola Peninsula until Chukotka Peninsula including both coastal area (predominantly) and inland territory. Strong wind speed events are often noted in the region in the cold time of year during the passage of meteorological synoptic storms. Wind speeds of more than 30 m∙s−1 are observed during this time over the marine surface, inducing high waves of more than 4 m.
A dataset of observed hourly 10-minute mean wind speed data from stations was obtained, with the record period varying from station to station. For the present study, we used the period 1966-2013, which was covered by data of all stations (Table 1). Their location is shown in Figure 1. Note that we do not consider here the matter of anemometer exposure. As with all analyses of wind data, the results of an extreme value analysis will be flawed if the data on which they are based are taken from an anemometer with a non-standard exposure (e.g., sheltered in one or more directions, or at a height above the ground different from the 10 m standard). Metadata for stations can be obtained from Meteorological Service of Russia.
It was interesting to observe exceptional outliers for several values (60 - 70 m∙s−1) in the dataset. As part of our analysis, we questioned whether to neglect this information as errors or spurious outliers. We investigated the reanalysis dataset to find such values. For this aim, a dataset of 3-hourly 10-m wind of the 20th Century Reanalysis dataset (1.9 × 1.875 deg. Lat. × Long.) for the period 1979-2004 was obtained [8] [9] . These data correspond to diagnostic values at the equivalent anemometer level. They differ little from other products [10] that are typically used for the Arctic region. This product was related directly to observations and in all cases we saw that it does not contain observed exceptional outliers. Therefore it seems logical that such velocities should were diagnosed as errors and ignored. However, as will be shown below, in some cases their appearance is possible.
A dataset of wind simulation of the INM-CM4 climate model for the period 1966-2005 was also obtained [11] . These data (1.5 × 2 deg. Lat. × Long.) correspond to the Historical experiment of the Coupled Model Intercomparison Project, Phase 5 (CMIP5) [12] . The use of station data will make it possible to evaluate the consistency between wind simulation products and near-surface observations. Observational data and the INM CM4 data cover not the same years, but it could not influence the statistical results due to specification of used numerical experiment, which focuses on generation of common features of modern climate conditions. Apart from, the appearances of extremes are not regular (Figure 2). Note that pictures in Figure 2(a) and Figure 2(b) are different in spite of the distance between stations is no more than 250 km. In this figures we can identify the long-term clusters of extreme events. Due to short observation period, it is not clear whether this is a sign of climate changes or a trace of long-lasting variations. The period of 1966-2013 characterizes the period of climate change [13] ; however, diagnosed events did not appear in statistics of wind speed events.
It is a condition of extreme value analysis that the extremes selected for examination have to be independent. Annual (or seasonal) maximum wind speeds chosen from each year are statistically independent. However, when several data points are taken from each season, there may well be several clustered maximum speeds from a single storm. Such events are unlikely to be statistically independent. Various strategies are invoked to remove dependent events before proceeding with a statistical analysis. A simple method is to require a minimum time separation or “deadtime” between selected events. Working with Arctic wind climate, we use the autocorrelation coefficient r(τ) to establish a deadtime between consequent wind fluctuations. Its value is a measure of the correlation of neighbouring wind events. It was shown to be less than 0.05 for τ equal to 48 or 72 hours. Therefore, we use a deadtime of 72 hours. The same values (48 - 60 h) were used earlier [14] - [16] .
![]()
Figure 1. Location of observation stations.
![]() (a)
(a)![]() (b)
(b)
Figure 2. Appearance of wind speed extremes (>21 m/s), based on wind observation at the Teriberka (a) and the Zimnegorsky Mayak (b) for cold period (from November (number of month is 11) to April (number is 4)) of each year.
3. The Weibull Distribution in Station Observation Data
Because it is widely accepted that the Weibull distribution is a good model for wind speed distributions, empirical extremes are modelled by the cdf:
 (1)
(1)
This expression (stretched exponential distribution) can be replaced by
 . (2)
. (2)
Such representation allows a straight representation of the empirical function on the coordinate axis of the Weibull distribution. The model parameters (A and k) can be estimated using the maximum likelihood approach. To estimate the success of approximation the coefficient of determination, denoted R2, is traditionally calculated. It provides a measure of how well observed outcomes are replicated by the model of linear regression, it is the square of the sample correlation coefficient. Such approach allows us to determine (almost visually) whether a simple estimate can approximate expression (1).
In Figure 3 we plot several empirical cdfs on the bases of station measurements. Configuration of empirical points in the form of columns is determined by the fact that the data are quantized due to specified accuracy of measurement. Pictures are the “Weibull Plots”, which are a specific nonlinear transformation of the data, and a straight line is recovered if the sample is Weibull. We can see that at all sites, we found that the empirical cdfs consistently deviate from the theoretical line starting with certain large threshold values (Uth). This means that the empirical tail diverges from the Weibull model, indicating that a different model might describe the data well. As a rule, there are only few such values (U > Uth); however, their presence has profound significance because they are the greatest extremes.
To approximate these empirical cdfs we use the same technique but applying Gumbel distribution. Again, as was expected, we found that the empirical cdfs consistently deviate from the theoretical model.
It is possible in such a situation to choose another function (including three parameters) for approximating the behaviour of observed data. However, we interpret these results in another way. It seems that data indicate that there is a violation of the above-mentioned condition of identically distributed random variables. The shape of the curve suggests that the volume of samples is composed of two sets of variables, each described by its own Weibull function. Figure 4 shows approximations of the empirical cdfs of wind speed extremes for different regions (same as in Figure 3) by two different Weibull distributions. Very large R-squared values (>0.95) denote the high success of this approximation. Coefficients of regression equations allow us to estimate parameters k and A in each cases.
For example, in Figure 5 we compare empirical cdf of wind speed extremes on the bases of the Teriberka station measurements (only data shown in Figure 4(a)) and corresponding Weibull distribution using calculated parameters: A = 1.64 × 10−5 and k = 3.97. To decide if samples come from a population with Weibull distribution the special statistical tests could be utilized. First of all note that R-squared values, denoting the success of the maximum likelihood approach, reflects in some aspects the Cramer-Mises-Smirnov (C-M-S) test, because it uses the integral of the squared difference between the empirical and the estimated distribution functions. If R2 ® 1 this means that the integral converge to zero. However, the C-M-S test cannot be used, because the information about the empirical function is incomplete since we have only values corresponding to U £ Uth. Similarly, the Anderson-Darling criterion cannot be applied because it places more weight on observations in the tails of the distribution which are out of reach. In this case more suitable the Kolmogorov-Smirnov (K-S) test because it uses the supremum of the absolute difference between the empirical and the estimated distribution functions. Here we take into consideration (using forms of regression lines―see Figure 4) that the supremum is not located in tail zone.
Because test is applied in contexts where a family of distribution is being tested, in which case the parameters of that family need to be estimated and account must be taken of this in adjusting either the test-statistic or its critical values. Revised critical values for Weibull distribution are given by [17] . Using the K-S test we assess that the null hypothesis, which asserts that the sample come from a population with Weibull distribution, cannot be rejected. Analogous procedure was used to decide if samples depicted in Figure 4(b) come from a population with Weibull distribution using another calculated parameters: A = 0.0120 and k = 1.77. It was concluded again that Weibull distribution fits well to the data (Figure 5(b)). The same result was established for other examples of Figure 4 and in all studied stations (Table 1).
Note additionally that application of a sufficiently high threshold and, consequently, detection of especially high wind speeds allows us to describe for their approximation the peaks-over-threshold modelling approach, using the Pareto distribution. It has a cumulative distribution function
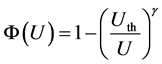 . (3)
. (3)
It is worth mentioning here that the threshold value is not assigned a priori (as is usually done [7] ) but is explicitly estimated previously.
Generally, the implemented analytical approach allows us to detect that the majority of extreme wind speed
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 3. Empirical cumulative distribution functions of wind speed maxima (station observations, cold period) for 72 hours time step records straightening on the coordinate axis of the Weibull distribution, and linear regression line corresponding to the Weibull function. (a) Teriberka, (b) Krasnochelie, (c) Zimnegorsky Mayak.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)![]() (d)
(d)![]() (e)
(e)![]() (f)
(f)
Figure 4. Empirical cumulative distribution functions of wind speed maxima (station observations, cold period) for 72 hours time step records straightening on the coordinate axis of the Weibull distribution, and linear regression line corresponding to the Weibull function. (a), (b) Teriberka, (c), (d) Krasnochelie, (e), (f) Zimnegorsky Mayak; (a), (c), (e) denotes the Weibull distribution for range U £ Uth (so-called “swans”―see below), (b), (d), (f) denotes the Weibull distribution for range U > Uth (so-called “dragons”―see below). In all cases R2 > 0.96.
![]() (a)
(a)![]() (b)
(b)
Figure 5. Fragments of empirical cdfs of wind speed extremes on the bases of the Teriberka station measurements and corresponding Weibull distribution using previously calculated parameters: (a) for data shown in Figure 4(a); (b) for data shown in Figure 4(b).
events (below the threshold value) adhere to the Weibull distribution. The same statistical distribution of population could be considered a result of the same organization principle, and this suggests a common generating mechanism for each representative of this population. This idea allows us to understand that a large extreme is not distinguished from its small siblings apart from its large power. The occurrence of large extremes looks like the appearance of a few black swans in a flock of white swans. This terminology was introduced by N.N. Taleb [18] , as a metaphor to describe an event that comes as a surprise.
However, there are extreme wind speed events located above the threshold value that are much more pronounced than predicted by the extrapolation of “black swans” law distributions in their tail. They adhere again to the Weibull distribution. Such events were termed “kings” (taking into account the special position of the fortune of kings, which appear to exist beyond the Zipf law distribution of the wealth of their subjects [19] ) or “dragons” (to stress that we address a completely different, beyond the normal, type of animal). D. Sornette [20] introduced the concept of dragon-kings to refer to such extreme events. The same statistical distribution suggests a common generating mechanism different from that responsible for extrema at U £ Uth.
It is not clear to what extent such excessively metaphoric terminology is required for our case because it was originally introduced to describe unique extraordinary events. However, it allows us to mark events that adhere to different Weibull distributions. Therefore, we will use below these terms: “swans” or “black swans” (hereafter Ss or BSs) and “dragons” (hereafter the Ds).
A very important message is that we can easily diagnose events adhering to the BSs or the Ds (in many cases the diagnostic of Ds is not simple and requires different methods adapted to the specific problem [20] ). In Figure 3, indeed, the Ds can be detected evidently based on obvious breaks in the tail of wind distributions. In statistics there is a test of the null hypothesis that two samples come from the same population against an alternative hypothesis, especially that a particular population tends to have larger values than the other. This is the Mann-Whitney U test (the Kruskal-Wallis test extends the Mann-Whitney U test when there are more than two groups). However, for comparing two (or more) sets of observations, they have to be a priori selected. In the case of wind speed extremes (or other meteorological extrema) such method is not possible, because all data refer to the same nomenclature.
Note that mentioned above exceptional outliers (“super extreme” wind speed events) are denoted along the line corresponding to the Ds distribution on the Weibull Plot. It means that their presence is not prohibited.
The Weibull distribution parameters calculated for all stations are shown in Table 2. Parameters are given separately for two groups of wind speed extremes come from the Ss and Ds populations. Note that events belonging to the Ds are not diagnosed in several cases.
4. The Question of Quantile Estimation
As was demonstrated, the Weibull distribution fits well with the data in all cases. Therefore, the estimated parameters (k and A) allow us to calculate the quantile (inverse cumulative distribution) function for the Weibull distribution as follows:
![]() . (4)
. (4)
Quantile wind speed values are calculated differently for the Ss and the Ds (Table 3). In our analysis, we have divided the data relating to cold and warm seasons. We have taken into account that in the Arctic region, July and August are the only true summer months, while the winter season covers not only December, January and February but also includes the whole interval from November to April. In these cases, taking into account the data volume (1966-2013) and remembering that time step records are 72 hours, the value of U(0.99) for the summer characterizes the maximum wind speed, which is exceeded, on average, once every five warm seasons. Similarly, the value of U(0.99) for the cold period of the year characterizes the maximum wind speed, which is exceeded, on average, two times every three cold seasons.
The dissimilarity between the Ds and the BSs can reach up to 30%, demonstrating both a difference in statistical properties and, probably, the differences of origin. The most pronounced feature of the geographical distribution of the quantile wind speed values is that the maxima (both the BSs and the Ds) are in the coastal area. As an example, for winter, U(0.99) = 24 ms−1 (the BS) and U(0.99) = 29 ms−1 (the Ds) are at the Teriberka station, (corresponding to 19 and 27 ms−1 at another coastal station, the Zimnegorsky Mayak), while for the Krasnochelie (the inland station of the Cola Peninsula), U(0.99) is 9 and 10 ms−1 for the BS and the Ds, respectively. During the summer, the geographical peculiarities are the same; however, absolute values are almost two times lower.
The “winter acceleration” of wind over the coastal area is not simply a consequence of a smooth sea surface, compared to land. An important role is played by storms that are typically much more active over the sea, especially during the cold season under the conditions of the non-freezing surface of the Barents Sea. During the warm season, the coastal/inland difference is not so pronounced and the quantile values are smaller.
The wind speed extremes observed at the surface should be a function of the meso-scale circulation [21] - [23] . It is a well-known fact that increased wind (e.g., wind gusts) originates from air parcels flowing at higher levels in the boundary layer that are deflected downward to the surface. Apart from meso-scale convective complexes we can note that some low level extremes involve the role of complex terrain as well as combinations of these processes. The most striking example (within the area of investigation) is demonstrated by the Maly Karmakula station where bora winds affect the eastern shore of the Barents Sea and wind speed can be ~40 ms−1 (see Table 3). Boras develop when cold air from the Kara Sea (typically covered by ice) is blocked by the Novaya Zemly Mountains, which rise to ~1000 m, but it can cross the mountains.
![]()
![]()
Table 2. The Weibull distribution parameters (k and A) calculated separately for two groups of wind speed extremes come from the Ss and Ds populations over the selected period 1966-2013 years (for wind speed in m/s).
![]()
Table 3. Quantile wind speed values U(0.99) in ms−1 (1966-2013) for wind data from measurement stations calculated separately for two groups of wind speed extremes come from the Ss and Ds populations.
5. The Weibull Distributions in Data of Climate Model Simulation
The next step of the analysis is to investigate to what extent the above-mentioned peculiarities of wind extremes are simulated by climate models. We analysed a dataset of wind simulation of the INM-CM4 climate model. The establishment of the correspondence between wind simulation products and near-surface observations could help us to assess the quality of modelling products and their capability to reproduce the wind extremes. Apart from that, it is important to advance our understanding of the origin of the BSs and the Ds.
In Figure 6(a), Figure 6(b), Figure 6(c) we plot several cdfs on the bases of the INM-CM4 simulations. For this aim we chose the INM-CM4 grid points located near the stations. We can conclude that the Weibull distribution is a good approximation of the modelled wind speed extremes. We find very small deviation in cdfs from the theoretical line starting with certain large threshold values. Let us remind that noticeable deviation was a typical feature of empirical cdfs (Figure 3 and Figure 4). Using our terminology, we can conclude that the INM-CM4 model wind speed extremes are the Ss and that there are no the Ds.
This conclusion is supported not only by the specific location of points along a theoretical line but also by the fact that modelled wind speed extremes themselves are close to observation data adhering the BSs besides the Zimnegorsky Mayak data and the Teriberka data, where observed U(0.99) are almost half times greater than modelled values (Table 4). Probably, this is due to inadequate distribution of land and sea in the INM-CM4. Their geographical peculiarities are the same (the maxima are at the coastal area).
The discovered phenomenon of the absence of the representatives of the Ds in modelling data is very important. Let us investigate this effect more precisely. Because extreme wind at the surface originates from air parcels that are deflected downward from the top of the boundary layer to the surface, we will focus on extremes in 850 hPa wind, which is likely to be more reliable than surface wind in an atmospheric model, as surface wind is more affected by unresolved topography and land/sea mask, and the model boundary layer scheme. Extremes in 850 hPa wind may be related to the potential for extreme surface wind speed [24] .
The results obtained (Figure 6(b), Figure 6(d), Figure 6(f)) indicate that the Weibull distribution is a good approximation of modelled wind speed extremes at the level H850. We find again the absence of deviation in cdfs from the theoretical line and can conclude that above the atmospheric boundary layer the set of modelled wind speed extremes do not consist of the Ds, they are the Ss. Note that in spite of difference of grid points location (inland area or coastal zones) the statistical features of modelled wind extremes are the same. For example, the quantile wind speed values at the level 850 hPa U(0.99) = 25 - 26 m/s for winter season and U(0.99) = 19 m/s for summer season (see Table 5). It means, that the geographical peculiarities of the near-surface wind speed extremes (see Table 4) originate due to air parcel subsidence occurring differently in the modelled atmospheric boundary layer over the coastal and inland area. In vicinity of coastal zone the modelled wind speed extremes at the level H850 are close to near-surface observation data, but within the inland territory the model overestimates the results of measurements (Table 5). However, this comparison is not meaningful because compared values are related to different populations (BSs and Ds) and hence their origin is different.
6. Conclusions
Extreme value analysis has been implemented to estimate the statistical properties of extreme wind speed over the European and Siberian parts of Arctic region from the Kola Peninsula to the Chukotka Peninsula. The application was made on 10-m wind speed data taken from the INM-CM4 climate model dataset and observation stations.
It was shown that for all stations a volume of observed samples of extreme wind speed are composed of two sets of variables. All samples of each population have the same statistical properties but one population is sharply different from another. So different origin of strong wind events adhering to two groups can be concluded. Using metaphoric terminology, we marked these events as the Ss (power extremes are the BSs) and the Ds. However, the modelled (INM-CM4 data) extreme wind speeds consist of only the Ss. Dissimilarity of the Ds and the BSs can reach up to 30%, hence, atmospheric model underestimates extreme wind speeds. The finding that global climate models are unable to capture the wind extremes is already well known, but information that the modelled (INM-CM4 data) extreme wind speeds do not consist of the Ds provides new knowledge.
This evidence indicates that the special mechanisms of the Ds are not reproduced by climate models which are utilized as a tool used to simulate climate change. Hence, the problem of identification of pronounced extreme wind speeds based on modelling data remains unresolved.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)![]() (d)
(d)![]() (e)
(e)![]() (f)
(f)
Figure 6. Cumulative distribution functions of wind speed maxima for cold period simulated by the INM-CM4 in the framework of the Historical experiment (CMIP 5) in grid points corresponded to the Zimnegorsky Mayak (a), (b), Kandalaksha (c), (d) and Krasnoshchelye (e), (f), near the surface (a), (c), (e) and at 850 hPa (b), (d), (f) for 72 hours time step records straightening on the coordinate axis of the Weibull low, and linear regression line corresponding to the Weibull function. In all cases R2 = 0.99.
![]()
Table 4. Quantile wind speed values (U(0.99), ms−1) near the surface for grid points corresponding to wind measurement stations across the Kola Peninsula and coastal zones of the Barents Sea and the White Sea (see Figure 1) based on data of the INM-CM4 and measurement stations.
![]()
Table 5. Quantile wind speed values (U(0.99), ms−1) at the level 850 hPa for grid points corresponding to wind measurement stations across the Kola Peninsula and coastal zones of the Barents Sea and the White Sea (see Figure 1) based on data of the INM-CM4, and quantile wind speed values (U(0.99), ms−1) near the surface based on data of measurement stations adhering to BSs and Ds (see Table 3).
It is well-known that large wind speed extremes observed at the surface are governed by the mesoscale atmospheric phenomena (embedded into strong synoptic storms) including both convective processes and effects of gravity waves, connecting to specific circulations (like the bora). Because such processes are not fully simulated by coarse spatial resolution atmospheric model, we could conclude that the largest wind speed extremes are not recreated by the climate models. It is important because the tasks demanding the information about wind speed extreme (for example, the task of projection of storminess intensity depending on the surface wind field) cannot be explicitly solved using the output of current climate model.
The mesoscale atmospheric models cover several aspects of such processes, the use of which has huge potential.
Acknowledgements
Funding for this research was provided by grants from the Russian Science Foundation (Grant No. 14-37-00038).