Air-Ground Temperature Coupling: Analysis by Means of Thermal Orbits ()
Received 7 December 2015; accepted 24 January 2016; published 27 January 2016

1. Introduction
Surface ground temperatures (SGT) and their dependence on surface air temperatures (SAT) are parameters of interest in a variety of environmental investigations. While SAT variations are mainly related to atmospheric factors, the ground temperature represents a complex output of a large number of physical, chemical and biological processes that occur over various temporal and spatial scales. The relative contribution of each process depends on the environment. On a local scale, this contribution varies with time through diurnal, seasonal and annual oscillations and reflects long-term changes that are caused by, e.g., land use and vegetation changes.
In the present study, we analyze air and shallow subsurface temperature series that were recorded during 1994-2010 at the experimental site of the Geothermal Climate Change Observatory (GCCO) at Sporilov (Prague) [1] . This experiment was completed with selected data from 2002 to 2013 from the ongoing experiment and focused on subsurface temperature studies under four different land cover types [2] . The objective of this work is to capture the regularities in the seasonal and annual behavior of surface air temperatures and surface ground temperature coupling to understand the relationship between these variables and to reveal the main mechanisms that are responsible for heat transport at the land-atmosphere boundary layer.
Temporal variations in the SGT-SAT differences (offset) are governed by numerous factors, such as short- wave and long-wave solar radiation, water cycle processes (precipitation, infiltration, evapotranspiration, runoff and subsurface flow), water phase changes and related processes (e.g., snow cover, freeze-thaw cycles), the vegetation cover and corresponding biological processes, terrain characteristics, and many others. The contributions of each of the above mechanisms on the heat exchange at the air-land interface and on the surface air and ground temperature coupling are complex [3] -[6] . Nevertheless, some general patterns of these SGT-SAT relationships only depend on a couple of dominant processes [7] . The set of these dominant processes depends on the environment and can be studied separately for each observational site.
The goal of this work is to investigate how air and ground temperature signals track each other over different scales and to describe the main mechanisms that are responsible for their decoupling. We use a phase-space representation of air and ground temperatures, specifically, 2D thermal orbits, to obtain insight into the processes that control seasonal/annual SGT-SAT coupling. We compare these SGT-SAT offsets with incident solar radiation to better elucidate the nature of the coupling.
Temperature time series are dominated by annual waves. One of the challenges of modern meteorology/cli- matology is the detection of longer periodicities that are hidden in noisy, highly variable temperature records, which reveal the underlying dynamics. In this work, we show that long-term periodicities which are hidden in temperature time series can be detected by means of thermal orbits.
2. Data
This temperature monitoring experiment, which was part of long-term paleoclimate studies, was initiated in a 38.3 m-deep borehole that was drilled in 1992 at the campus of the Geophysical Institute in Prague-Sporilov (50˚02'27"N, 14˚28'39"E, 274 m a.s.l.) [1] . The experiment began on January 1, 1994; the data that were used in this report cover from January 5, 1994 to March 23, 2010. In 2002, a nearby complex polygon site (50˚02'26"N, 14˚28'32"E, 276 m a.s.l.) was added to monitor the air temperature and shallow subsurface temperatures under four different land cover types within the uppermost 0.5-m layer [2] . In 2007, the polygon was completed by meteorological instrumentation, including measurements of precipitation and incident and reflected solar radiation.
The data in this work were aggregated into time series of monthly means. Figure 1 illustrates the monthly means of air and ground temperature time series at several depths (from the year 1994 to 2010). Similarly to most meteorological records, surface air temperature oscillations represent a periodic pattern (annual wave) that is contaminated by a certain amount of noise. The “signature” of the annual wave fades away and substantially decreases with depth. Thus, all ground temperature signals are modestly attenuated (with the corresponding filtering of the high frequency variations) and phase-shifted relative to the SAT. The 0.05-m depth contains a noticeable linear warming trend of 0.111 K/yr that, similarly to other surface perturbations, slowly vanishes during downward propagation. For example, this trend is suppressed to 0.058 and 0.051 K/yr at 20 and 25 m, respectively.
The ground temperature time series do not contain significant perturbations, and the conductive heat transfer process generally dominates over the monthly scale. However, the air-soil surface interaction and the underground heat transport may involve some non-conductive processes, and temperature differences DT (SGT-SAT) may occur in all seasons. The air warms up and cools down more quickly than the ground. During the summer, the air becomes warm long before the ground does (DT < 0). During the winter, the air cools down more rapidly
![]()
Figure 1. Monthly air and ground temperature records at several depth levels (Sporilov hole) from 1994 to 2010.
than the ground does (DT > 0). The offset values predominantly depend on the local climate of the observation site [8] .
While the daily and annual weather periodicities, which reflect obvious and predictable Earth rotation and orbit scenarios, can be easily detected and quantified, the presence of non-conductive perturbations, which generally appear as weak, irregular and short time-scale events, need further processing and more artful analyzing methods to understand.
3. Theoretical Considerations
A qualitative version of the thermal orbit (TO) method was presented by Beltrami [3] and further quantificated by Smerdon et al. [6] . The TO approach is based on the perpendicular superposition of the two variables x(t) and y(t) on 2D x-y graphs. When both variables are periodic functions (e.g., monthly means of air/ground temperatures and numerous other meteorological parameters with prevailing annual waves), the output graph represents a typical Lissajous figure. The latter represents curves that appear in 2-D graphs when the x and y variables are given by two sine or cosine waves, which may have any amplitude, frequency and phase. The temperature signals that arise from damping of the annual variations in surface air temperature during their penetration into the ground represent one of the typical cases of waves with equal frequency (Figure 2). We assumed purely conductive heat transport within a 1-D semi-infinite medium with constant thermophysical properties (the thermal diffusivity k in this and further theoretical models was 10−6 m2/s). The surface air temperature represents a single
wave , where T is the temperature, z is the depth and t is the time. Furthermore,
, where T is the temperature, z is the depth and t is the time. Furthermore,
we assume an annual period T0, an amplitude A of 1 K and a zero mean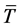 . If the surface signal mainly propagates into the soil by conduction, its periodic nature remains, while the amplitude and phase decrease with depth:
. If the surface signal mainly propagates into the soil by conduction, its periodic nature remains, while the amplitude and phase decrease with depth:
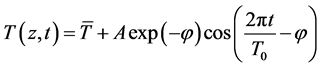 ,
,
where 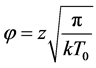 [9] . In this case, the air versus ground temperature plots represent elliptical phase-space or-
[9] . In this case, the air versus ground temperature plots represent elliptical phase-space or-
bits (Thermal Orbit, TO) with parameters that depend on the amplitude attenuation and the phase shift of the
![]()
Figure 2. Left: Theoretical (pure conductive) time series of air, 1-m, 5-m and 10-m depth temperatures for an annual cycle with a thermal diffusivity of k = 10−6 m2/s. Right: Corresponding theoretical thermal orbits (ellipses).
ground temperature. When two sine waves are in-phase, the TO represents a diagonal line; when they have the same amplitude and a 90 degree phase lag, the TO is a circle. If the periods of the sine waves do not coincide, the appearance of the resulting TOs is more complex. However, if the ratios of their periods are rational, the resulting plot always represents a closed curve (orbit).
The presence of natural noise results in an indistinct or malformed (saw-like) ellipse border, but it never distorts its regular form. The ellipse remains invariable even at relatively high noise levels in the measured data, and the really significant deformations only occur as a result of serious disturbances in the periodic regime, such as continuous air-ground surface temperature inconsistencies or decoupling.
The construction of the TOs can be effective for quick diagnostics of the thermal regime in the subsurface. The deformations of elliptic orbits that are caused by the provisional operation of non-conductive processes can be identified by a simple look. The advantage is that this approach does not require regularly measured data, and the occurrence of data gaps in the obtained date series is not an obstacle.
Above, we discussed the case of plotting two “one-harmonics” temperature signals against each other (thermal orbits, TO). In general, a Lissajous figure represents a comparison of 1) signals with different periods and/or more than one wave; 2) periodic signals of different physical variables (mixed orbits) and 3) more than two periodic signals (e.g., air and ground temperatures and incident solar radiation), whose relationship provides information about the interactions of different variables and the underlying processes.
4. Results
4.1. Thermal Orbits
4.1.1. One Harmonics Thermal Orbits
The TO method was applied to air/ground temperature signals that were averaged over a monthly scale. The ground temperature varies from month to month in accordance with the variations in the incident solar radiation and from season to season for the overlying air temperature. The series of averaged SGT and/or SAT values are dominated by the annual periodicity, and their TOs should present clear ellipses. Any deviation from a pure periodic regime will manifest itself as an ellipse border disturbance, which can be easily identified.
Figure 3 shows a comparison of the TOs from the monthly means of air temperature at 0.05 m height (SAT) and ground temperature at 0.05 m depth (SGT) for several individual years. The shape of all the orbits is generally elliptic. The length of the major axis reflects the range of the annual variations in both temperatures, while the minor axis depends on the degree of the ΔT (SGT-SAT) offset. The sequence exhibits insignificant variations from year to year. The ellipses that were calculated for the individual years practically mirror each other. The air is generally warmer than the ground (negative offset) from March to September, while the ground is warmer that the air (positive offset) during late autumn and winter. In other words, heat flows into the ground during spring and summer and flows upwards from the ground during fall and winter. This behavior of the heat flow at the air-soil interface was detected in other works [10] . The ΔT (SGT-SAT) offset value varies throughout
![]()
Figure 3. Thermal orbits for monthly air temperature means at 0.05 m height and soil temperature means at 0.05 m depth for 1998-2000 and 2008-2010. The shape and position of the orbit does not change much during this time.
the year. The strongest coupling between both temperatures can be generally observed during the summer (absolute values of offset are less than 1 K), while noticeable disturbances in the elliptical TO can be observed during the winter (up to 3 - 4 K).
On the whole, the data provided small interannual ΔT (SGT-SAT) temperature offsets. A similar conclusion was confirmed by González-Rouco et al. [11] , who reported that the SGT and SAT are practically indistinguishable from each other at the interannual and longer time scales. Mann et al. [12] showed that the air temperature has a dominant influence on the ground temperature during warm seasons. Smerdon et al. [8] concluded that the connection between SAT and SGT at interannual time scales is stable and appears closer during the summer than during the winter. Thus, the SGT represents a confident proxy for annual surface air temperatures.
The detailed SGT-SAT coupling over a single year is more complex. Its seasonal evolution is a function of corresponding changes in meteorological conditions. Several seasonal processes can increase these SGT-SAT differences. Latent heat fluxes within the subsurface occur through evapotranspiration during the summer [4] , and through freezing and thawing cycles during the winter [3] [6] . Snow cover influences temperatures and heat transfer in the subsurface [13] [14] . These factors generally produce cooler/warmer mean daily SGTs relative to SATs during the summer and winter, respectively. Smerdon et al. [5] [8] investigated the ΔT (SGT-SAT) offsets at various locations with diverse climates (including Prague, Sporilov) and showed that the decoupling of both temperatures occurred both in cold and warm (summer/winter) seasons, but the degree, timing and distribution were strongly affected by local climate conditions.
Winter snowfall and occasional freezing or thawing cycles may represent major causes of breaking in one- by-one SGT-SAT tracking during cold seasons. Numerous authors [3] [6] [15] investigated the perturbations in annual thermal orbits that were caused by changing land surface processes in cold environments. For example, snow operates as an effective insulator, protecting the soil from cold air temperatures during the winter. Variations in ground temperature under black frost conditions are generally larger than those when the ground is protected by snow cover [14] . The so-called “zero curtain” effect probably creates the most obvious TO distortions. During frosty days, the air temperature falls below zero, and the latent heat that is released by soil moisture freezing keeps the soil temperatures close to 0˚C until the entire water content has frozen [13] .
4.1.2. Detection of Multi-Periodic Dynamics in Temperature Time Series by Means of Thermal Orbits
Meteorological records may contain longer-scale periodicities in addition to the dominancy of daily and annual waves. Cermak et al., who applied Recurrence Quantification Interval (RQI) analysis and calculated the heterogeneity power spectra of the Sporilov temperature time series, reported the potential existence of multi-year cycles that correspond to periods of approximately 14, 8 and 2 - 3 years [1] . Similar periodicities were confirmed in a number of meteorological series (see e.g. [15] [16] ).
A direct application of conventional statistical methods may sometimes fail because recorded time series are often inhomogeneous, too short or non-continuous; continuity and adequately long observation intervals are essential requirements for their successful use. On the other hand, the TO approach can be successfully applied not only to rapidly detect any inconsistencies between SAT and SGT but also to reveal the existence of long-term regularities. A periodicity of ~8 years was presumed in the Sporilov temperature time series compared with an amplitude of 0.6 K in the surface temperatures, which differs from the 8 K amplitude that corresponds to an annual wave with an insignificant phase lag of 0.2 between both waves [1] . In such a case, the theoretical temperature time series that are calculated for the one-harmonics annual wave alone and for the sum of both waves practically coincide even in an ideal noise-free case. Because the 8-year periodicity is hardly visible in the actual temperature monitoring data, the TO technique provides a unique possibility for fast detection.
Figure 4 and Figure 5 illustrate the downwards propagation of the surface temperature wave, which repre- sents the sum of the annual wave (amplitude 10 K, phase lag 0) and the 8-year wave (amplitude 1 K, phase lag 0). The chosen values are similar to those for the Sporilov temperature time series. The TO graphs show thermal orbits for the 1-, 5-, and 10-m depth temperatures. Simple ellipses that are characteristic of one-cycle dynamics transform into complex voluminous saddle-type curves that can be easily distinguished from the one-cycle ellipses. The gradual distinction of saddle-like orbits from the perfect ellipses grows with depth.
Figure 6 shows the TO graphs for monthly averaged temperatures at different depths in the Sporilov hole. At shallower depths, the shape of the orbits is generally elliptic and corresponds to the damped harmonic oscillations that are illustrated in Figure 2. This tendency is generally preserved in the upper ~5 m depth interval; below this depth, the form of the TOs begins to differ, and the 5- and 10-m depth orbits become more like the theoretical orbits in Figure 5, which supports the potential presence of multiple-cycle dynamics.
The reason for the more explicit appearance of longer-scale periodicities in deeper TOs is the strong modulation of the near-surface temperature-time records by annual waves that contain certain noise. During pure conductive downward penetration, the surface signal is progressively smoothed down and the amplitudes of the periodic waves substantially decrease. The “fingerprints” of high-frequency components quickly decrease. In the above theoretical example, the amplitudes 10 and/or 1 K, which correspond to 1- and 8-year surface waves, decrease to 7.29/0.89, 2.06/0.57 and 0.43/0.33 K at 1, 5 and 10 m, respectively. Both waves become comparable at 10 m, and their TOs do not differ substantially. In other words, weak and short-period events disappear at deeper levels, and only pronounced and longer-period (“time-resistant”) events are visible in deeper records. The
![]()
Figure 4. Theoretical time series of air, 1-m, 5-m and 10-m depths for annual and combined annual plus 8-year cycles.
![]()
Figure 5. Theoretical thermal orbits for one-cycle (red) and two-cycle (black) processes at different depths.
![]()
Figure 6. Thermal orbits from monthly means of the surface ground temperature vs ground temperature records at various depths.
low-frequency features that were hidden under large amounts of noise in the near surface temperature series become clearly observable in deeper thermal orbits and can be easily recognized on sight.
4.2. Mixed Orbits
Above, we applied the TO approach to the temperature vs temperature relationship; however, Lissajous figures (orbits) can, in principle, be constructed from any pair of periodic functions. The phase-space representations of temperature time series with other meteorological variables can thus be used for a quick diagnostics of other features of their interdependence. The detection of the relationships between borehole temperature data and other meteorological or climatic variables may represent an essential step in research and facilitate the examination of the underlying physical processes [17] and the development of multiple linear regression models that relate ground temperatures to other climatic information [18] [19] .
Various meteorological processes influence the surface and ground temperatures by affecting the heat exchange rate between the atmosphere and the ground. The amount, timing and distribution of the SGT-SAT offset may be strongly affected by local climate conditions when the incident solar radiation represents the most important factor that controls the SGT-SAT coupling. We have analyzed the hourly, daily and seasonal ground-air temperature differences ΔT (SGT-SAT) in a broader context of their coupling with the incident solar radiation. To formally distinguish from the term “Thermal Orbit” (TO) that is used for the temperature-temperature comparison, we use the term “Mixed Orbits” (MO) for the orbits that are constructed for the superposition of different variables in the following text.
The observed relationship between the ΔT (SGT-SAT) offset and the incident solar radiation for the GCCO Sporilov is presented in Figure 7. To stress the role of the solar radiation’s impact on the ground temperature conditions, only “day” values are shown, namely, observations between 07:00 and 19:00 hours. Although the high daily variability of the solar radiation reflects the corresponding variability of local meteorological conditions, clear linear relationships were obtained at both investigated time scales. The correlation is negative. Greater differences occur when the incident solar radiation is more intensive. This negative correlation is more noticeable for the hourly offset values. The obtained slope value suggests that the absolute value of the offset increases by ~1 K for every 100 W/m2 of radiation growth.
The mode of the DT vs radiation relationship depends on the ground surface properties, namely, the land cover type. Under grassy cover, the slope of the DT-radiation relationship is negative. Under a “barren” surface (such as sand or rock), the slope value is positive [1] . Similarly, a generally positive linear correlation between the SGT-SAT offset and observed incident solar radiation was found at Emigrant Pass Observatory (EPO), Utah [20] , where the authors attributed the observed phenomenon to local specific surface conditions, such as the lack of vegetation at the surface and the low porosity of the local granite medium. A strong reduction in the water content within the uppermost ground layer decreases the effect of the water’s latent heat at the air-ground interface and increases the impact of the radiant heating on temperature. This problem is, however, more complicated; an opposite result was reported by Beltrami [3] at the Pomquet Station (Nova Scotia), who found an inverse correlation for the difference between soil (at 1-m depth) and air temperatures and the amount of incoming solar radiation.
The main features of the solar radiation time series are their diurnal and annual periodicities. Because the intensity of the solar radiation depends on the angle of incidence, the daily and seasonal changes in the Sun’s position govern the amount of solar radiation. On flat surfaces, the radiation is most intense when the Sun is overhead and declines when the Sun goes down; at night, the radiation is null. The Earth’s surface thus receives
![]()
Figure 7. Ground-air temperature differences (offset) versus incident solar radiation. The individual dots represent the means of the hourly (gray) and daily (red) values that were calculated for the year 2009 data series.
more solar energy during midday than early morning or late afternoon. Similarly, the length of the energy intake is an important factor; at 50˚ northern latitude, the daily amount of received solar energy is about three times higher during summer months than winter months. Except for the above periodic components, certain irregular variations in the solar radiation amount may occur because of local/temporary changes in weather conditions (cloud cover changes, wind, etc.).
Figure 8 represents the perpendicular superposition of the DT (SGT-SAT) offsets with an incident solar radiation for the year 2009 and its four individual seasons. The MO orbits allow one to track both the diurnal and seasonal evolution of the coupling of both variables. All the MOs (with the exception of the summer JJA orbit) appear as regular ellipses. The daily cycle is seen as a first order variation and generally confirms the periodic nature of the interdependence of both variables. The incident solar radiation reaches its maximum at about noon (
12:00
hours), which is very visible according to the arrangement of the major axes of the ellipses. Ellipse deformations only occur at the zero radiation line and are caused by the absence of solar radiation during the night. Except for this fact, no other potential distortions are present in the orbits. Despite the complexity of the heat transfer processes within the subsurface active layer, the ΔT (SGT-SAT) offset is only determined by the strength of the incident solar radiation, and no other substantial disturbances to the conductive heat transfer that are associated, e.g., with temporal variations in thermal diffusivity, evaporation, snow cover, or freeze-thaw events are present.
The smallest MOs are observable during the winter (maximum solar radiation ~100 - 150 W/m2), and the ΔT values are positive (SGT > SAT) during the entire winter (the ground is warmer than the air during days and nights). The MOs for the fall (SON) and spring (MAM) seasons are similarly regular, without significant disturbances, but they appear in a slightly more “corpulent” manner, exhibiting both positive and negative offsets. The shallow ground temperature is cooler than the air above (ΔT < 0) during the day for all seasons except winter. Noticeable ΔT/radiation variations (the largest MO) occur during summer months because of the growing intake of solar energy. The highest negative SGT-SAT offsets (~5 K) occur at high values of solar radiation and remain nearly constant (flattening of the ellipse) within the warmest time interval, when the radiation amount remains at the highest daily level of ~250 - 600 W/m2 (corresponding to daily afternoon periods between ~13 - 18 hours). This MO deformation (“cut” of the orbit) is only characteristic during the summer period.
5. Concluding Remarks
In this work, we examined how SGT variations are connected with SAT variations and tested the hypothesis that borehole temperatures could be used as a reliable proxy of the SAT. We investigated ΔT (SGT-SAT) differences over seasonal and annual scales to reveal the main factors that led to SGT-SAT decoupling over longer periods.
![]()
Figure 8. Orbits (ellipses) of the ground-air temperature offset shown against incident solar radiation for seasonal and annual data that were calculated for the 2009 period. Each data point represents the average value of all hourly means of the investigated time series corresponding to the specific hour.
The fast, semi-qualitative thermal/mixed orbit technique was employed to determine the nature of the heat transfer regime at the air-ground interface and subsurface. Two types of orbit techniques were applied to the two- decade-long surface air and ground temperature time series that were measured at the GCCO site (Prague, Sporilov) to investigate how SAT and SGT signals tracked each other over different time scales and to examine the dependence of their offset on other meteorological factors.
The major results can be summarized as follows:
1) Annual cycles and corresponding regular elliptic thermal orbits represent first order variations. Records of air and soil temperatures from the GCCO site indicate that the ground temperature tracks air temperature variations throughout the year. These results confirmed the dominant effect of air temperature and solar radiation on the ground surface temperatures.
2) The obtained results confirmed that the GST variations are related to the SAT variations and that the borehole temperatures could be used as a reliable proxy of the SAT at the mid-latitudes of Europe. This fact represents an advantage compared to higher latitude stations, where an accurate GST-SAT coupling should be accepted with caution.
3) The ground, because of its unique damping and filtering capacity, can mask short-term temperature fluctuations and thus emphasize long time-scale variations (periodicities) that are not detectable in the SAT series because of the existing amount of random noise. Such hidden periodicities can be captured from borehole temperature series that are recorded at depth by means of the TO technique.
4) Previous investigations were devoted to temperature-temperature time series comparisons within the TO approach. However, Lissajous figures (orbits) can be constructed from any pair of periodic functions. In this work, we developed the TO technique and showed that the phase-space representations of temperature time series with other meteorological variables (MO) could be used for a quick diagnostics of the important features of their interdependence. We demonstrated that the dynamics of the GST-SAT offset evolution which corresponded to the variations in the controlling meteorological variables could be discovered simply by examining the mixed orbits by sight.
Acknowledgements
Support was provided by the Grant Agency of the Czech Republic (project GACR P210/11/0183) and by the program LG13040 (MSMT-9344/2013-31.