1. Introduction
Let  be a graph with vertex set V and edge set E, and let C be a set of colors. An edge-coloring of G is to color all the edges in E so that any two adjacent edges are colored with different colors in C. The minimum number of colors required for edge-colorings of G is called the chromatic index, and is denoted by
be a graph with vertex set V and edge set E, and let C be a set of colors. An edge-coloring of G is to color all the edges in E so that any two adjacent edges are colored with different colors in C. The minimum number of colors required for edge-colorings of G is called the chromatic index, and is denoted by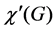 . It is well-known that
. It is well-known that 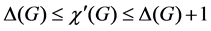 for every simple graph G and that
for every simple graph G and that 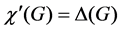 for every bipartite (multi)graph G, where
for every bipartite (multi)graph G, where 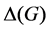 is the maximum degree of G [1]. The ordinary edge-coloring problem is to compute the chromatic index
is the maximum degree of G [1]. The ordinary edge-coloring problem is to compute the chromatic index 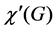 of a given graph G and find an edge-coloring of G using
of a given graph G and find an edge-coloring of G using 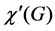 colors. Let
colors. Let  be a cost function which assigns an integer
be a cost function which assigns an integer  to each color
to each color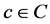 , then the cost
, then the cost
edge-coloring problem is to find an optimal edge-coloring of G, that is, an edge-coloring f such that ![]()
is minimum among all edge-colorings of G. An optimal edge-coloring does not always use the minimum number ![]() of colors. For example, suppose that
of colors. For example, suppose that ![]() and
and ![]() for each index
for each index![]() , then the graph G with
, then the graph G with ![]() in Figure 1(a) can be uniquely colored with the three cheapest colors
in Figure 1(a) can be uniquely colored with the three cheapest colors![]() ,
, ![]() and
and ![]() as in Figure 1(a), but this edge-coloring is not optimal; an optimal edge-coloring of G uses the four cheapest colors
as in Figure 1(a), but this edge-coloring is not optimal; an optimal edge-coloring of G uses the four cheapest colors![]() ,
, ![]() ,
, ![]() and
and![]() , as illustrated in Figure 1(b). However, every simple graph G has an edge-coloring
, as illustrated in Figure 1(b). However, every simple graph G has an edge-coloring
using ![]() or
or ![]() colors [2] [3]. The edge-chromatic sum problem, introduced by Giaro and Kubale [4], is merely the cost edge-coloring problem for the special case where
colors [2] [3]. The edge-chromatic sum problem, introduced by Giaro and Kubale [4], is merely the cost edge-coloring problem for the special case where ![]() for each integer
for each integer![]() .
.
The cost edge-coloring problem has a natural application for scheduling [5]. Consider the scheduling of biprocessor tasks of unit execution time on dedicated machines. An example of such tasks is the file transfer problem in a computer network in which each file engages two corresponding nodes, sender and receiver, simultaneously [6]. Another example is the biprocessor diagnostic problem in which links execute concurrently the same test for a fault tolerant multiprocessor system [7]. These problems can be modeled by a graph G in which machines correspond to the vertices and tasks correspond to the edges. An edge-coloring of G cor- responds to a schedule, where the edges colored with color ![]() represent the collection of tasks that are executed in the ith time slot. Suppose that a task executed in the ith time slot takes the cost
represent the collection of tasks that are executed in the ith time slot. Suppose that a task executed in the ith time slot takes the cost![]() . Then the goal is to find a schedule that minimizes the total cost, and hence this corresponds to the cost edge-coloring problem.
. Then the goal is to find a schedule that minimizes the total cost, and hence this corresponds to the cost edge-coloring problem.
The cost edge-coloring problem is APX-hard even for bipartite graphs [8], and hence there is no polynomial- time approximation scheme (PTAS) for the problem unless![]() . On the other hand, Zhou and Nishizeki gave an algorithm to solve the cost edge-coloring problem for trees T in time
. On the other hand, Zhou and Nishizeki gave an algorithm to solve the cost edge-coloring problem for trees T in time![]() , where n is the number of vertices in T,
, where n is the number of vertices in T, ![]() is the maximum degree of T, and
is the maximum degree of T, and ![]() is the maximum absolute cost
is the maximum absolute cost ![]() of colors c in C [5]. The algorithm is based on a dynamic programming (DP) approach, and computes a DP table for each vertex of a given tree T from the leaves to the root of T. In this paper, we give a polynomial-time algorithm to solve the cost edge-coloring problem for cacti. In our best knowledge, this is the first polynomial- time algorithm to find an optimal edge-coloring of a cactus.
of colors c in C [5]. The algorithm is based on a dynamic programming (DP) approach, and computes a DP table for each vertex of a given tree T from the leaves to the root of T. In this paper, we give a polynomial-time algorithm to solve the cost edge-coloring problem for cacti. In our best knowledge, this is the first polynomial- time algorithm to find an optimal edge-coloring of a cactus.
2. Preliminaries
In this section, we define some basic terms.
Let ![]() be a graph with a set V of vertices and a set E of edges. We sometimes denote by
be a graph with a set V of vertices and a set E of edges. We sometimes denote by ![]() and
and ![]() the vertex set and the edge set of G, respectively. We denote by
the vertex set and the edge set of G, respectively. We denote by ![]() and
and![]() , respectively, or simply by n and m, the number of vertices and edges in G, that is,
, respectively, or simply by n and m, the number of vertices and edges in G, that is, ![]() and
and![]() . The degree
. The degree ![]() of a vertex v is the number of edges in E incident to v. We denote the maximum degree of G by
of a vertex v is the number of edges in E incident to v. We denote the maximum degree of G by ![]() or simply by
or simply by![]() . A cactus G can be represented by an under tree T, which is a rooted tree. In the underlay tree T of G, each node represents a block which is either a bridge (edge) of G or an elementary cycle of G. If there is an edge between nodes
. A cactus G can be represented by an under tree T, which is a rooted tree. In the underlay tree T of G, each node represents a block which is either a bridge (edge) of G or an elementary cycle of G. If there is an edge between nodes ![]() and
and ![]() of T, then bridges or cycles of G represented by
of T, then bridges or cycles of G represented by ![]() and
and ![]() share exactly one vertex in G. Each node b of T corresponds to a subgraph
share exactly one vertex in G. Each node b of T corresponds to a subgraph ![]() of G induced by all bridges and cycles represented by the nodes that are descendants of b in T. Figure 2(a) depicts the subgraph
of G induced by all bridges and cycles represented by the nodes that are descendants of b in T. Figure 2(a) depicts the subgraph ![]() for the child
for the child ![]() of the root r of T. Clearly
of the root r of T. Clearly ![]() and
and ![]() is a cactus for each node b of T. One can easily find an underlay tree T of a given cactus G in linear time, and hence one may assume that an underlay tree of G is given. We denote by
is a cactus for each node b of T. One can easily find an underlay tree T of a given cactus G in linear time, and hence one may assume that an underlay tree of G is given. We denote by ![]() the number of edges joining a node b and its children in T. Then,
the number of edges joining a node b and its children in T. Then, ![]() , and
, and ![]() for every vertex
for every vertex![]() .
.
Let C be a set of colors. An edge-coloring ![]() of a graph G is to color all edges of G by colors in C so that any two adjacent edges are colored with different colors. Let
of a graph G is to color all edges of G by colors in C so that any two adjacent edges are colored with different colors. Let![]() , where
, where ![]() is the set of real numbers. One may assume with loss of generality that
is the set of real numbers. One may assume with loss of generality that ![]() is non-decreasing, that is,
is non-decreasing, that is, ![]() for any
for any
![]() (a) (b)
(a) (b)
Figure 2. (a) A cactus; and (b) its under tree.
index i,![]() . Since trivially any graph G has an optimal edge-coloring using colors at most
. Since trivially any graph G has an optimal edge-coloring using colors at most![]() , we assume for the sake of convenience that
, we assume for the sake of convenience that![]() , and we write
, and we write![]() . The cost
. The cost ![]() of an edge-coloring f of a graph
of an edge-coloring f of a graph ![]() is defined as follows:
is defined as follows:
![]()
An edge-coloring f of G is called an optimal one if ![]() is minimum among all edge-colorings of G. The cost edge-coloring problem is to find an optimal edge-coloring of a given graph G. The cost of an optimal edge-coloring of G is called the minimum cost of G, and is denoted by
is minimum among all edge-colorings of G. The cost edge-coloring problem is to find an optimal edge-coloring of a given graph G. The cost of an optimal edge-coloring of G is called the minimum cost of G, and is denoted by![]() .
.
Let f be an edge-coloring of a graph G. For each vertex v of G, let ![]() be the set of all colors that are assigned to edges incident to v, that is,
be the set of all colors that are assigned to edges incident to v, that is,
![]()
We say that a color ![]() is missing at v if
is missing at v if![]() . Let
. Let ![]() be the set of all colors missing at v, that is,
be the set of all colors missing at v, that is,![]() .
.
3. Algorithm
In this section we prove the following theorem.
Theorem 1. An optimal edge-coloring of a cactus can be found in polynomial time.
As a proof of Theorem 1, we give a dynamic programming algorithm in the remainder of this section to compute the minimum cost ![]() of a given cactus G. Our algorithm can be easily modified so that it actually finds an optimal edge-coloring f of G with
of a given cactus G. Our algorithm can be easily modified so that it actually finds an optimal edge-coloring f of G with![]() .
.
A dynamic programming method is a standard one to solve a combinatorial problem on graphs with tree- construction. We also use it, and compute the minimum cost ![]() of a cactus G with an under tree T by the bottom-up tree computation.
of a cactus G with an under tree T by the bottom-up tree computation.
3.1. Ideas and Definitions
Let b be a node of T with its parent![]() , and let v be the vertex on both two blocks b and
, and let v be the vertex on both two blocks b and![]() . Let
. Let ![]() be the children of b in T. Then one can observe that the minimum cost
be the children of b in T. Then one can observe that the minimum cost ![]() of the subgraph
of the subgraph ![]() rooted at b cannot be computed directly from the minimum costs
rooted at b cannot be computed directly from the minimum costs ![]() of all the subgraphs
of all the subgraphs![]() ,
,![]() . Our idea is to introduce a new parameter
. Our idea is to introduce a new parameter ![]() defined for each node b of T and each pair of colors
defined for each node b of T and each pair of colors ![]() as follows:
as follows:
![]()
If ![]() has no such edge-coloring we define
has no such edge-coloring we define![]() . Note that
. Note that ![]() if either the block b is an edge and
if either the block b is an edge and ![]() or the block b is a cycle and
or the block b is a cycle and![]() . Clearly,
. Clearly,
![]()
We compute the values ![]() for all indices
for all indices![]() ,
, ![]() , from leaves to root r. Thus the DP table for each node b consists of the
, from leaves to root r. Thus the DP table for each node b consists of the ![]() values
values![]() ,
,![]() .
.
Our algorithm computes ![]() for all pairs of colors
for all pairs of colors ![]() from the leaves to the root r of T, by means of dynamic programming. Then
from the leaves to the root r of T, by means of dynamic programming. Then ![]() can be computed at the root r from all the values
can be computed at the root r from all the values ![]() as follows:
as follows:
![]()
and it can be computed in polynomial time. Thus the remainder problem is how to compute all the values ![]() for each node
for each node ![]() of T and all pairs of colors
of T and all pairs of colors![]() .
.
3.2. Algorithm
In this subsection, we explain how to compute all the values ![]() for each node
for each node ![]() of T and all pairs of colors
of T and all pairs of colors![]() .
.
3.2.1. The Node b Is a Leaf in T
In this case, the block b is either an edge or a cycle. Therefore we have the following two cases to consider.
Case 1: the block b is an edge.
In this case, clearly
![]()
and all the values![]() ,
, ![]() , can be computed in time polynomial in
, can be computed in time polynomial in![]() .
.
Case 2: the block b is a cycle.
In this case, we describe the following algorithm to compute ![]() in time polynomial in the size of
in time polynomial in the size of ![]() and
and![]() .
.
![]()
3.2.2. The Node b Is an Internal Node
In order to compute ![]() for each pair of indices
for each pair of indices ![]() and
and![]() ,
, ![]() , we introduce a new parameter
, we introduce a new parameter ![]() defined as follows.
defined as follows.
Let ![]() be a set of blocks of T such that all these blocks share exactly one vertex v in G. For each pair of colors
be a set of blocks of T such that all these blocks share exactly one vertex v in G. For each pair of colors ![]() we define
we define
![]()
We show how to compute the all the values ![]() from the
from the ![]() values
values![]() ,
, ![]() and
and![]() . The problem of computing
. The problem of computing ![]() can be reduced to the minimum cost flow problem on a bipartite graph
can be reduced to the minimum cost flow problem on a bipartite graph ![]() as follows.
as follows.
We first introduce ![]() isolated vertices
isolated vertices![]() ,
, ![]() and
and![]() . Then add
. Then add ![]() vertices
vertices![]() ,
, ![]() , corresponding to colors
, corresponding to colors![]() , and add a source s and a sink t. Connect the source s to all the
, and add a source s and a sink t. Connect the source s to all the ![]() vertices
vertices![]() ,
, ![]() , with capacity 1 and cost 0. For each vertex
, with capacity 1 and cost 0. For each vertex![]() ,
, ![]() and
and![]() , connect
, connect ![]() to all the vertices
to all the vertices![]() ,
, ![]() and
and![]() , satisfying
, satisfying ![]() or
or ![]() with capacity 1 and cost 0. Finally, for each vertex
with capacity 1 and cost 0. Finally, for each vertex![]() ,
, ![]() and
and![]() , connect
, connect ![]() to the sink t with capacity 2 and cost
to the sink t with capacity 2 and cost![]() . The minimum cost flow problem is to find a maximum flow from s to t with the sum of costs of edges on the flow. Clearly
. The minimum cost flow problem is to find a maximum flow from s to t with the sum of costs of edges on the flow. Clearly ![]() is equal to the cost of the minimum cost maximum flow in
is equal to the cost of the minimum cost maximum flow in![]() .
.
The minimum cost maximum flow problem can be solved in time polynomial in the size of the graph [9] [10], and hence the value ![]() for a pair of indices
for a pair of indices ![]() and
and![]() ,
, ![]() , can be computed in time polynomial in
, can be computed in time polynomial in ![]() and
and ![]() since
since ![]() has at most
has at most ![]() vertices and edges. Therefore the
vertices and edges. Therefore the ![]() values
values ![]() for all pairs of indices
for all pairs of indices ![]() and
and![]() ,
, ![]() , can be computed total in time polynomial in
, can be computed total in time polynomial in ![]() and
and![]() .
.
We are now ready to compute![]() . Since the block b is either an edge or a cycle, we have the following two cases to consider.
. Since the block b is either an edge or a cycle, we have the following two cases to consider.
Case 1: the block b is an edge![]() .
.
Let ![]() be the set of blocks of the children of b in T. Then all the blocks
be the set of blocks of the children of b in T. Then all the blocks ![]() share exactly one vertex v in G. In this case, clearly
share exactly one vertex v in G. In this case, clearly
![]()
and it can be computed in time polynomial in the size of ![]() and
and![]() .
.
Case 2: the block b is a cycle.
In this case, let ![]() be the vertices lied on the cycle of
be the vertices lied on the cycle of ![]() in the clockwise order. Assume that
in the clockwise order. Assume that ![]() is the vertex shared by the block b and its parent block, and let
is the vertex shared by the block b and its parent block, and let![]() ,
, ![]() , be the set of blocks which shares
, be the set of blocks which shares![]() ;
; ![]() if no such blocks exist. In order to compute
if no such blocks exist. In order to compute ![]() we define
we define
![]() (1)
(1)
for each j, ![]() , where
, where![]() . Then clearly
. Then clearly
![]()
Therefore it suffices to show how to compute ![]() in polynomial time for each j,
in polynomial time for each j, ![]() , as follows.
, as follows.
By Equation (1) we have
![]()
and hence ![]() for all j,
for all j, ![]() , can be recursively computed total in time
, can be recursively computed total in time ![]() if all the values
if all the values![]() ,
, ![]() , are given. Since we have mentioned before that all the values
, are given. Since we have mentioned before that all the values ![]() can be computed in time polynomial in
can be computed in time polynomial in ![]() and
and![]() , one can compute all
, one can compute all ![]() and hence
and hence ![]() total in time polynomial in
total in time polynomial in ![]() and
and![]() .
.
4. Conclusion
In this paper, we show that the cost edge-coloring problem for a cactus G can be solved in polynomial time. It is still open to solve the problem in polynomial time for outerplanar graphs.
Supported
This work is partially supported by grants of the thousand talent plan of Zhejiang province.