1. Introduction and Statements of the Results
Let  be a polynomial of degree n and denote by
be a polynomial of degree n and denote by . Then we have the following well-known Bernstein’s inequality [1] .
. Then we have the following well-known Bernstein’s inequality [1] .
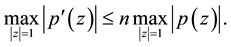 (1.1)
(1.1)
Equality holds in (1.1) if and only if 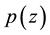 has all its zeros at the origin.
has all its zeros at the origin.
Inequality (1.1) can be sharpened if we restrict ourselves to the class of polynomials having no zeros in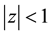 . In fact, it was conjectured by Erdösand later verified by Lax [2] that if
. In fact, it was conjectured by Erdösand later verified by Lax [2] that if 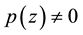 in
in , then
, then
 (1.2)
(1.2)
Inequality (1.2) is the best possible and equality attains for ,
,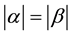 .
.
Malik [3] extended (1.2) by considering the class of polynomials 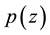 of degree n not vanishing in
of degree n not vanishing in![]() ,
, ![]() , and proved
, and proved
![]() . (1.3)
. (1.3)
As a generalization of (1.3), Bidkham and Dewan [4] proved that if ![]() was a polynomial of degree n having no zero in
was a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() ,
,
![]() (1.4)
(1.4)
Equality holds in (1.4) for![]() .
.
Further, Dewan and Mir [5] obtained the following result which was a generalization as well as an improvement of (1.4).
Theorem A. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() ,
,
![]() (1.5)
(1.5)
Let ![]() be a polynomial of degree n and let
be a polynomial of degree n and let ![]() denote the polar derivative
denote the polar derivative ![]() with respect to a point
with respect to a point![]() , then
, then
![]()
The polynomial ![]() is of degree at most
is of degree at most ![]() and it generalizes the ordinary derivative in the sense that
and it generalizes the ordinary derivative in the sense that
![]()
Aziz [6] extended (1.3) to the polar derivative of ![]() by showing that if
by showing that if ![]() had no zero in
had no zero in![]() ,
, ![]() , the for every real or complex number
, the for every real or complex number ![]() with
with![]() ,
,
![]() (1.6)
(1.6)
Inequality (1.6) is the best possible and equality holds for ![]() with a real number
with a real number![]() , and
, and![]() .
.
In this paper, we establish the following result, which deduces to a result giving, in turn, a generalization as well as an extension of Theorem A to polar derivative. In fact, we prove:
Theorem 1. If![]() , is a polynomial of degree n having no zero in
, is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() , and for every real or complex number
, and for every real or complex number ![]() with
with![]() ,
,
![]() (1.7)
(1.7)
The result is the best possible and equality occurs for![]() ,
, ![]() with a real number
with a real number![]() .
.
Remark 1. For![]() ,we have
,we have
![]() (1.8)
(1.8)
Also, for![]() , inequality (1.8) holds trivially and hence inequality (1.8) is true for
, inequality (1.8) holds trivially and hence inequality (1.8) is true for![]() . Using this fact in the above theorem, we have:
. Using this fact in the above theorem, we have:
Corollary 1. If![]() , is a polynomial of degree n having no zero in
, is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() , and for every real or complex number
, and for every real or complex number ![]() with
with![]() ,
,
![]() (1.9)
(1.9)
It is seen that Corollary 1 is a generalization as well as an extension of a result due to Dewan and Mir [5] into polar derivative.
Dividing both sides of (1.9) by ![]() and making
and making![]() , we obtain the following, which is an extension of the theorem due to Dewan and Mir [5] .
, we obtain the following, which is an extension of the theorem due to Dewan and Mir [5] .
Corollary 2. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() ,
,
![]() (1.10)
(1.10)
The result is the best possible and the extremal polynomial is![]() ,
,![]() .
.
Remark 2. Both the inequalities (1.7) and (1.9) of Theorem 1 and Corollary 1, respectively reduce to inequality (1.6) for![]() .
.
Further, it was shown by Turán [7] that if ![]() is a polynomial of degree n having all its zeros in
is a polynomial of degree n having all its zeros in![]() , then
, then
![]() . (1.11)
. (1.11)
The result is sharp and equality in (1.11) holds if all the zeros ![]() lie on
lie on![]() .
.
As an extension of (1.11), Malik [3] showed that if ![]() has all its zeros in
has all its zeros in![]() ,
, ![]() , then
, then
![]() (1.12)
(1.12)
whereas, if ![]() has all its zeros in
has all its zeros in![]() ,
, ![]() , then Govil [8] proved that
, then Govil [8] proved that
![]() (1.13)
(1.13)
Both the estimates (1.12) and (1.13) are sharp. Equality in (1.12) holds for![]() ,
, ![]() whereas equality in (1.13) holds for
whereas equality in (1.13) holds for![]() ,
,![]() .
.
Although the above result is sharp but still it is easy to see that it has two drawbacks. Firstly, the bound in (1.13) depends only on the zero of largest modulus and not on other zeros even if some of them are very close to the origin. Secondly, since the extremal polynomial in (1.13) is![]() , it should be possible to obtain a better
, it should be possible to obtain a better
bound for the polynomials![]() , where not all the co-efficients
, where not all the co-efficients ![]() are zero. It would, therefore, be interesting to obtain a bound which depends on the location of all the zeros of the polynomial
are zero. It would, therefore, be interesting to obtain a bound which depends on the location of all the zeros of the polynomial ![]() and also on the co-efficients
and also on the co-efficients![]() . In this connection, Dewan et al. [9] proved.
. In this connection, Dewan et al. [9] proved.
Theorem B. If![]() ,
, ![]() is a polynomial of degree
is a polynomial of degree ![]() such that
such that![]() ,
, ![]() , and
, and![]() , then
, then
![]() (1.14)
(1.14)
and
![]() (1.15)
(1.15)
The result is the best possible and equality in (1.14) and (1.15) holds for![]() .
.
Aziz and Rather [10] obtained a result which not only extended (1.12) into polar derivative of![]() , but also was a generalization by proving that if all the zeros of the polynomial
, but also was a generalization by proving that if all the zeros of the polynomial ![]() of degree n lie in
of degree n lie in ![]() where
where![]() , then for every real or complex number
, then for every real or complex number ![]() with
with![]() ,
,
![]() . (1.16)
. (1.16)
The result is sharp and equality holds for ![]() with
with![]() .
.
While, the corresponding extension which was also a generalization of (1.13) for![]() , was done by Rather [11] who proved that if all the zeros of the polynomial
, was done by Rather [11] who proved that if all the zeros of the polynomial ![]() of degree n lie
of degree n lie![]() ,
, ![]() , then for every real or complex number
, then for every real or complex number ![]() with
with![]() ,
,
![]() (1.17)
(1.17)
Next, we further prove the following theorem in which inequality (1.18) not only extends inequality (1.14) into polar derivative but is also a generalization, while inequality (1.19) extends inequality (1.15) into polar derivative.
Theorem 2. If![]() ,
, ![]() is polynomial of degree
is polynomial of degree![]() , such that
, such that![]() ,
, ![]() , and if
, and if![]() , then for every real or complex number
, then for every real or complex number ![]() with
with![]() , and
, and ![]() for
for![]() ,
,
![]() (1.18)
(1.18)
and
![]() (1.19)
(1.19)
If we divide both sides of (1.18) and (1.19) by ![]() and make
and make![]() , we obtain inequalities (1.14) and (1.15) respectively.
, we obtain inequalities (1.14) and (1.15) respectively.
Remark 3. For polynomials of degree![]() , Theorem 2 gives a refinement of inequality (1.17) due to Rather [11] .
, Theorem 2 gives a refinement of inequality (1.17) due to Rather [11] .
Since ![]() for
for![]() , Theorem 2 gives, in particular:
, Theorem 2 gives, in particular:
Corollary 3. If![]() ,
, ![]() , is a polynomial of degree
, is a polynomial of degree ![]() having all its zeros in
having all its zeros in![]() ,
, ![]() , then for every real or complex number
, then for every real or complex number ![]() with
with![]() ,
, ![]() for
for![]() ,
,
![]() (1.20)
(1.20)
and
![]() (1.21)
(1.21)
Remark 4. For ![]() and
and![]() ,
, ![]() and
and ![]() are both increasing functions of x and so the expressions
are both increasing functions of x and so the expressions
![]()
and
![]()
are always non-negative so that for polynomials of degree![]() , inequalities (1.20) and (1.21) together provide a refinement of inequality (1.17). In fact, excepting the case when
, inequalities (1.20) and (1.21) together provide a refinement of inequality (1.17). In fact, excepting the case when ![]() has all its zeros on
has all its zeros on![]() , with
, with![]() ,
, ![]() ,
, ![]() and
and![]() , the bound obtained in Theorem 2 is always sharper than the bound obtained from inequality (1.17).
, the bound obtained in Theorem 2 is always sharper than the bound obtained from inequality (1.17).
2. Lemmas
We require the following lemmas for the proofs of the theorems.
Lemma 2.1. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then
, then
![]()
The above result is due to Govil et al. [12] .
Lemma 2.2. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() ,
,
![]() .
.
There is equality in (2.2) for![]() .
.
Lemma 2.2 is due to Jain [13] .
Lemma 2.3. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then the function
, then the function
![]() (2.2)
(2.2)
is a non-decreasing function of t in![]() .
.
Proof of Lemma 2.3.We prove this by derivative test. Now, we have
![]() ,
,
which is non-negative since ![]() (see Remark 1 with m = 1) [14] and the fact that
(see Remark 1 with m = 1) [14] and the fact that![]() .
.
Lemma 2.4. If ![]() is a polynomial of degree n having no zero in
is a polynomial of degree n having no zero in![]() ,
, ![]() , then for
, then for![]() ,
,
![]() (2.3)
(2.3)
Inequality (2.3) is the best possible for![]() ,
,![]() .
.
Remark 5. Lemma 2.4 is of independent interest because by employing the simple fact that
![]()
of Remark 1, it gives a result which extends the theorem due to Dewan and Kaur [15] .
The proof of Lemma 2.4 follows on the same lines as that of Lemma 2.3 due to Dewan and Mir [5] , but for the sake of completeness we give a brief outline of its proof.
Proof of Lemma 2.4. Since ![]() has no zero in
has no zero in![]() ,
, ![]() , the polynomial
, the polynomial ![]() where
where ![]() has no zero in
has no zero in![]() , where
, where![]() . Hence applying Lemma 2.1 to the polynomial
. Hence applying Lemma 2.1 to the polynomial![]() , we get
, we get
![]() ,
,
which implies
![]() . (2.4)
. (2.4)
Now, for ![]() and
and![]() , we have
, we have
![]() (using (2.4))
(using (2.4))
which implies on using (2.2) of Lemma 2.2,
![]()
which gives for![]() ,
,
![]() (2.5)
(2.5)
For![]() , by Lemma 2.3, we have
, by Lemma 2.3, we have
![]() (2.6)
(2.6)
Using (2.6) to (2.5), we have
![]()
which completes the proof of Lemma 2.4.
Lemma 2.5. If ![]() is a polynomial of degree
is a polynomial of degree![]() , then for
, then for![]() ,
,
![]() (2.7)
(2.7)
and
![]() (2.8)
(2.8)
Lemma 2.5 is due to Dewan et al. [9] .
Lemma 2.6. If ![]() is a polynomial of degree
is a polynomial of degree ![]() having all its zeros in
having all its zeros in![]() , then for
, then for![]() ,
,
![]() (2.9)
(2.9)
and
![]() (2.10)
(2.10)
The result is sharp and equality in (2.9) and (2.10) holds for![]() , where
, where ![]() and
and![]() .
.
This result is also due to Dewan et al. [9] .
3. Proof of the Theorems
Proof of Theorem 1. Since the polynomial ![]() has no zero in
has no zero in![]() ,
, ![]() , it follows that
, it follows that ![]() has no zero in
has no zero in![]() , where
, where![]() . Applying inequality (1.6) to the polynomial
. Applying inequality (1.6) to the polynomial ![]() and noting that
and noting that![]() , we have
, we have
![]()
or
![]() ,
,
which is equivalent to
![]() . (3.1)
. (3.1)
For ![]() and
and![]() , inequality (3.1) when combined with Lemma 2.4, we get
, inequality (3.1) when combined with Lemma 2.4, we get
![]() ,
,
hence the proof of Theorem 1 is completed.
Proof of Theorem 2. We first prove inequality (1.8). Since the zeros of ![]() are
are![]() ,
, ![]() , the zeros of the polynomial
, the zeros of the polynomial ![]() are
are![]() ,
, ![]() , and because the polynomial
, and because the polynomial ![]() has all its zeros in
has all its zeros in![]() ,
, ![]() , the polynomial
, the polynomial ![]() has all its zeros in
has all its zeros in![]() . Hence for every real or complex number
. Hence for every real or complex number ![]() with
with![]() , we have by inequality (1.16) with
, we have by inequality (1.16) with![]() ,
,
![]()
or
![]()
which is equivalent to
![]()
or
![]() . (3.2)
. (3.2)
Since the polynomial ![]() is of degree
is of degree![]() , and also by our assumption, the co-efficient of
, and also by our assumption, the co-efficient of ![]() in the polar derivative
in the polar derivative ![]() viz.,
viz., ![]() , it follows that
, it follows that ![]() is a polynomial of degree
is a polynomial of degree![]() . Thus, applying (2.7) of Lemma 2.5 to
. Thus, applying (2.7) of Lemma 2.5 to ![]() with
with![]() , we get
, we get
![]() (3.3)
(3.3)
Combining (3.2) and (3.3), we get
![]() (3.4)
(3.4)
Let ![]() be the reciprocal polynomial of
be the reciprocal polynomial of![]() . Since
. Since ![]() has all its zeros in
has all its zeros in![]() ,
, ![]() ,
, ![]() , it follows that the polynomial
, it follows that the polynomial ![]() has all its zeros in
has all its zeros in ![]() and is of degree
and is of degree![]() . Applying inequality (2.9) of Lemma 2.6 to
. Applying inequality (2.9) of Lemma 2.6 to ![]() for
for![]() , we get
, we get
![]()
which is equivalent to
![]()
which gives
![]() (3.5)
(3.5)
Combining (3.4) and (3.5), we get
![]()
which on simplification yields
![]()
which proves inequality (1.18) completely.
The proof of inequality (1.19) follows on the same lines as that of (1.18), but instead of applying (2.7) of Lemma 2.5 and (2.9) of Lemma 2.6, inequalities (2.8) and (2.10) respectively of Lemmas 2.5 and 2.6 are used.