1. Introduction
In 1873 French mathematician, Charles Hermite, proved that 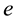 is transcendental. Coming as it did 100 years after Euler had established the significance of
is transcendental. Coming as it did 100 years after Euler had established the significance of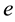 , this meant that the issue of transcendence was one mathematicians could not afford to ignore. Within 10 years of Hermite’s breakthrough, his techniques had been extended by Lindemann and used to add
, this meant that the issue of transcendence was one mathematicians could not afford to ignore. Within 10 years of Hermite’s breakthrough, his techniques had been extended by Lindemann and used to add 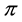 to the list of known transcendental numbers. Mathematician then tried to prove that other numbers such as
to the list of known transcendental numbers. Mathematician then tried to prove that other numbers such as ![]() and
and ![]() are transcendental too, but these questions were too difficult and so no further examples emerged till today’s time. The transcendence of
are transcendental too, but these questions were too difficult and so no further examples emerged till today’s time. The transcendence of ![]() has been proved in 1929 by A. O. Gel’fond.
has been proved in 1929 by A. O. Gel’fond.
Conjecture 1. Whether the both numbers ![]() and
and ![]() are irrational.
are irrational.
Conjecture 2. Whether the numbers ![]() and
and ![]() are algebraically independent.
are algebraically independent.
However, the same question with ![]() and
and ![]() has been answered:
has been answered:
Theorem. (Nesterenko, 1996 [1] ) The numbers ![]() and
and ![]() are algebraically independent.
are algebraically independent.
Throughout of 20-th century,a typical question: whether ![]() is a transcendental number for each algebraic number
is a transcendental number for each algebraic number ![]() has been investigated and answered many authors .Modern result in the case of entire functions satisfying a linear differential equation provides the strongest results, related with Siegel’s E-functions [1] [2] , ref [1] contains references to the subject before 1998, including Siegel
has been investigated and answered many authors .Modern result in the case of entire functions satisfying a linear differential equation provides the strongest results, related with Siegel’s E-functions [1] [2] , ref [1] contains references to the subject before 1998, including Siegel ![]() and
and ![]() functions.
functions.
Theorem. (Siegel C. L.) Suppose that ![]()
![]() (1.1)
(1.1)
Then ![]() is a transcendental number for each algebraic number
is a transcendental number for each algebraic number ![]()
Let ![]() be an analytic function of one complex variable
be an analytic function of one complex variable ![]()
Conjecture 3. Whether ![]() is an irrational number for given transcendental number
is an irrational number for given transcendental number ![]()
Conjecture 4. Whether ![]() is a transcendental number for given transcendental number
is a transcendental number for given transcendental number ![]()
In this paper we investigate the arithmetic nature of the values of ![]() at transcendental points
at transcendental points ![]()
Definition 1.1. Let ![]() be any real analytic function such that
be any real analytic function such that
![]() (1.2)
(1.2)
We will call any function given by Equation (1.2) ![]() -analytic function and denoted by
-analytic function and denoted by ![]()
Definition 1.2. [3] [4] . A transcendental number ![]() is called #-transcendental number over the field
is called #-transcendental number over the field![]() , if there does not exist
, if there does not exist ![]() -analytic function
-analytic function ![]() such that
such that ![]() i.e. for every
i.e. for every ![]() -analytic function
-analytic function ![]() the inequality
the inequality ![]() is satisfies.
is satisfies.
Definition 1.3. [3] [4] . A transcendental number ![]() is called w-transcendental number over the field
is called w-transcendental number over the field![]() , if
, if ![]() is not #-transcendental number over the field
is not #-transcendental number over the field![]() , i.e. there exists
, i.e. there exists ![]() -analytic function
-analytic function ![]() such that
such that ![]()
Example. Number ![]() is transcendental but number
is transcendental but number ![]() is not
is not ![]() -transcendental number over the field
-transcendental number over the field ![]() as
as
(1) function ![]() is a
is a ![]() -analytic and
-analytic and
(2) ![]() i.e.
i.e.
![]() (1.3)
(1.3)
Main results are.
Theorem 1.1. [3] [4] . Number ![]() is #-transcendental over the field
is #-transcendental over the field![]() .
.
From theorem 1.1 immediately follows.
Theorem 1.2. Number ee is transcendental.
Theorem 1.3. [3] [4] . The both numbers ![]() and
and ![]() are irrational.
are irrational.
Theorem 1.4. For any ![]() number
number ![]() is #-transcendental over the field
is #-transcendental over the field![]() .
.
Theorem 1.5. [3] [4] . The both numbers ![]() and
and ![]() are irrational.
are irrational.
Theorem 1.6. [3] [4] . Let ![]() be a polynomials with coefficients in
be a polynomials with coefficients in![]() .
.
Assume that for any ![]() algebraic numbers over the field
algebraic numbers over the field![]() ,
, ![]() form a complete set of the roots of
form a complete set of the roots of ![]() such that
such that
![]() (1.4)
(1.4)
and![]() . Assume that
. Assume that
![]() (1.5)
(1.5)
Then
![]() (1.6)
(1.6)
2. Preliminaries. Short Outline of Dedekind Hyperreals and Gonshor Idempotent Theory
Let ![]() be the set of real numbers and
be the set of real numbers and ![]() a nonstandard model of
a nonstandard model of ![]() [5] .
[5] . ![]() is not Dedekind complete.
is not Dedekind complete.
For example, ![]() and
and ![]() are bounded subsets of
are bounded subsets of ![]() which have no suprema or infima in
which have no suprema or infima in
![]() . Possible completion of the field
. Possible completion of the field ![]() can be constructed by Dedekind sections [6] [7] . In [6] Wattenberg constructed the Dedekind completion of a nonstandard model of the real numbers and applied the construction to obtain certain kinds of special measures on the set of integers. Thus was established that the Dedekind com- pletion
can be constructed by Dedekind sections [6] [7] . In [6] Wattenberg constructed the Dedekind completion of a nonstandard model of the real numbers and applied the construction to obtain certain kinds of special measures on the set of integers. Thus was established that the Dedekind com- pletion ![]() of the field
of the field ![]() is a structure of interest not for its own sake only and we establish further im- portant applications here. Important concept introduced by Gonshor [7] is that of the absorption number of an ele- ment
is a structure of interest not for its own sake only and we establish further im- portant applications here. Important concept introduced by Gonshor [7] is that of the absorption number of an ele- ment ![]() which, roughly speaking, measures the degree to which the cancellation law
which, roughly speaking, measures the degree to which the cancellation law ![]() fails for
fails for![]() .
.
2.1. The Dedekind Hyperreals ![]()
Definition 2.1. Let ![]() be a nonstandard model of
be a nonstandard model of ![]() [5] and
[5] and ![]() the power set of
the power set of![]() .
.
A Dedekind hyperreal ![]() is an ordered pair
is an ordered pair ![]() that satisfies the next conditions:
that satisfies the next conditions:
1. ![]() 2.
2. ![]() 3.
3. ![]()
4. ![]() 5.
5. ![]()
Compare the Definition 2.1 with original Wattenberg definition [6] ,(see [6] def.II.1).
Designation 2.1. Let ![]() We designate in this paper
We designate in this paper
![]()
Designation 2.2. Let ![]() We designate in this paper
We designate in this paper
![]()
Remark 2.1. The monad of ![]() is the set:
is the set: ![]() is denoted by
is denoted by![]() .
.
Supremum of ![]() is denoted by
is denoted by![]() . Supremum of
. Supremum of ![]() is denoted by
is denoted by![]() . Note that [6]
. Note that [6]
![]()
Let ![]() be a subset of
be a subset of ![]() bounded above. Then
bounded above. Then ![]() exists in
exists in ![]() [6] .
[6] .
Example 2.1. 1)![]() , 2)
, 2) ![]()
Remark 2.2. Unfortunately the set ![]() inherits some but by no means all of the algebraic structure on
inherits some but by no means all of the algebraic structure on![]() . For example,
. For example, ![]() is not a group with respect to addition since if
is not a group with respect to addition since if ![]() denotes the addition in
denotes the addition in ![]() then:
then:
![]() Thus
Thus ![]() is not even a ring but pseudo-ring only.
is not even a ring but pseudo-ring only.
Definition 2.2. We define:
1. The additive identity (zero cut) ![]() often denoted by
often denoted by ![]() or simply 0 is
or simply 0 is
![]()
2. The multiplicative identity ![]() often denoted by
often denoted by ![]() or simply 1 is
or simply 1 is
![]()
Given two Dedekind hyperreal numbers ![]() and
and ![]() we define:
we define:
3. Addition ![]() of
of ![]() and
and ![]() often denoted by
often denoted by ![]() is
is
![]()
It is easy to see that ![]() for all
for all ![]()
It is easy to see that ![]() is again a cut in
is again a cut in ![]() and
and ![]()
Another fundamental property of cut addition is associativity:
![]()
This follows from the corresponding property of![]() .
.
4. The opposite ![]() of
of![]() , often denoted by
, often denoted by ![]() or simply by
or simply by![]() , is
, is
![]()
5. We say that the cut ![]() is positive if
is positive if ![]() or negative if
or negative if ![]()
The absolute value of![]() , denoted
, denoted![]() , is
, is![]() , if
, if ![]() and
and ![]() if
if ![]()
6. If ![]() then multiplication
then multiplication ![]() of
of ![]() and
and ![]() often denoted
often denoted ![]() is
is
![]()
In general, ![]() if
if ![]() or
or![]() ,
, ![]() if
if ![]() or
or ![]()
![]() if
if ![]() or
or ![]()
7. The cut order enjoys on ![]() the standard additional properties of:
the standard additional properties of:
(i) transitivity: ![]()
(ii) trichotomy: eizer ![]() or
or ![]() but only one of the three
but only one of the three
(iii) translation: ![]()
2.2. The Wattenberg Embeding ![]() into
into ![]()
Definition 2.3. [6] . Wattenberg hyperreal or #-hyperreal is a nonepty subset ![]() such that:
such that:
(i) For every ![]() and
and ![]()
![]()
(ii) ![]()
(iii) ![]() has no greatest element.
has no greatest element.
Definition 2.4. [6] . In paper [6] Wattenberg embed ![]() into
into ![]() by following way:
by following way:
If ![]() the corresponding element,
the corresponding element, ![]() of
of ![]() is
is
![]() (2.1)
(2.1)
Remark 2.3. [6] . In paper [6] Wattenberg pointed out that condition (iii) above is included only to avoid nonuniqueness. Without it ![]() would be represented by both
would be represented by both ![]() and
and ![]()
Remark 2.4. [7] . However in paper [7] H. Gonshor pointed out that the definition (2.1) in Wattenberg paper [6] is technically incorrect. Note that Wattenberg [6] defines ![]() in general by
in general by
![]() (2.2)
(2.2)
If ![]() i.e.
i.e. ![]() has no mininum, then there is no any problem with definitions (2.1) and (2.2). However if
has no mininum, then there is no any problem with definitions (2.1) and (2.2). However if ![]() for some
for some ![]() i.e.
i.e. ![]() then according to the latter definition (2.2)
then according to the latter definition (2.2)
![]() (2.3)
(2.3)
whereas the definition of ![]() requires that:
requires that:
![]() (2.4)
(2.4)
but this is a contradiction.
Remark 2.5. Note that in the usual treatment of Dedekind cuts for the ordinary real numbers both of the latter sets are regarded as equivalent so that no serious problem arises [7] .
Remark 2.6. H. Gonshor [7] defines ![]() by
by
![]() (2.5)
(2.5)
Definition 2.5. (Wattenberg embeding) We embed ![]() into
into ![]() of the following way: (i) if
of the following way: (i) if ![]() the corresponding element
the corresponding element ![]() of
of ![]() is
is
![]() (2.6)
(2.6)
and
![]() (2.7)
(2.7)
or in the equivalent way,i.e. if ![]() the corresponding element
the corresponding element ![]() of
of ![]() is
is
![]() (2.8)
(2.8)
Thus if ![]() then
then ![]() where
where
![]() (2.9)
(2.9)
Such embeding ![]() into
into ![]() Such embeding we will name Wattenberg embeding and to designate by
Such embeding we will name Wattenberg embeding and to designate by![]() .
.
Lemma 2.1. [6] .
(i) Addition ![]() is commutative and associative in
is commutative and associative in![]() .
.
(ii) ![]()
(iii) ![]()
Remark 2.7. Notice, here again something is lost going from ![]() to
to ![]() since
since ![]() does not imply
does not imply ![]() since
since ![]() but
but ![]()
Lemma 2.2. [6] .
(i) ![]() a linear ordering on
a linear ordering on ![]() often denoted
often denoted![]() , which extends the usual ordering on
, which extends the usual ordering on![]() .
.
(ii) ![]()
(iii) ![]()
(iv) ![]() is dense in
is dense in![]() . That is if
. That is if ![]() in
in ![]() there is an
there is an ![]() then
then ![]()
(v) Suppose that ![]() is bounded above then
is bounded above then ![]() exist in
exist in![]() .
.
(vi) Suppose that ![]() is bounded below then
is bounded below then ![]() exist in
exist in![]() .
.
Remark 2.8. Note that in general case ![]() In particular the formula for
In particular the formula for ![]()
given in [6] on the top of page 229 is not quite correct [7] , see Example 2.2. However by Lemma 2.2 (vi) this is no problem.
Example 2.2. [7] . The formula ![]() says
says
![]()
Let ![]() be the set
be the set ![]() where
where ![]() runs through the set of all positive numbers in
runs through the set of all positive numbers in![]() , then
, then ![]() However
However ![]()
Lemma 2.3. [6] .
(i) If ![]() then
then ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
Proof. (v) By (iv): ![]()
(1) Suppose now ![]() this means
this means
(2) ![]() and therefore
and therefore
(3) ![]()
(4) Note that: ![]() (since
(since ![]() and
and ![]() imply
imply ![]() but this is a contradiction)
but this is a contradiction)
(5) Thus ![]() and therefore
and therefore ![]()
(6) By similar reasoning one obtains: ![]()
(7) Note that: ![]() and therefore
and therefore
![]()
Lemma 2.4. (i) ![]()
(ii) ![]()
Proof. (i) For ![]() the statement is clear. Suppose now without loss of generality
the statement is clear. Suppose now without loss of generality ![]() By Lemma 2.3. (iv):
By Lemma 2.3. (iv): ![]()
(1) Suppose ![]() and therefore
and therefore ![]() but this means
but this means
(2) ![]() and therefore
and therefore
(3) ![]()
(4) Note that: ![]() (since
(since ![]() and
and ![]() imply
imply ![]() but this is a contradiction)
but this is a contradiction)
(5) Thus ![]() and therefore
and therefore ![]()
(6) By similar reasoning one obtains: ![]()
(7) Note that: ![]() and therefore
and therefore
![]()
(ii) Immediately follows from (i) by Lemma 2.3.
Definition 2.6. Suppose![]() . The absolute value of
. The absolute value of ![]() written
written ![]() is defined as follows:
is defined as follows:
![]()
Definition 2.7. Suppose ![]() The product
The product![]() , is defined as follows: Case (1)
, is defined as follows: Case (1)![]() :
:
![]() (2.10)
(2.10)
Case (2) ![]()
Case (3) ![]()
![]() (2.11)
(2.11)
Lemma 2.5. [6] . (i) ![]()
(ii) Multiplication ![]() is associative and commutative:
is associative and commutative:
![]() (2.12)
(2.12)
(iii) ![]()
![]() where
where ![]()
(iv) ![]()
(v)![]() (2.13)
(2.13)
(vi)![]() (2.14)
(2.14)
Lemma 2.6. Suppose ![]() and
and ![]() Then
Then
![]() (2.15)
(2.15)
Proof. We choose now:
(1) ![]() such that:
such that: ![]()
(2) Note that ![]()
Then from (2) by Lemma 2.4. (ii) one obtains
(3) ![]() Therefore
Therefore
(4) ![]()
(5) Then from (4) by Lemma 2.5. (v) one obtains
(6) ![]()
Then from (6) by Lemma 2.4. (ii) one obtains
(7) ![]()
Definition 2.8. Suppose ![]() then
then ![]() is defined as follows:
is defined as follows:
(i) ![]()
(ii) ![]()
Lemma 2.7. [6] .
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
![]()
(v) ![]()
(vi) ![]()
Lemma 2.8. [6] . Suppose that ![]() Then
Then
![]()
Theorem 2.1. Suppose that ![]() is a non-empty subset of
is a non-empty subset of ![]() which bounded from above, i.e.
which bounded from above, i.e. ![]() exist and suppose that
exist and suppose that ![]() Then
Then
![]() (2.16)
(2.16)
Proof. Let ![]() Then
Then ![]() is the smallest number such that, for any
is the smallest number such that, for any ![]() Let
Let ![]() Since
Since ![]() for any
for any ![]() Hence
Hence ![]() is bounded above by
is bounded above by ![]() Hence
Hence ![]() has a supremum
has a supremum ![]() Now we have to prove that
Now we have to prove that ![]() Since
Since ![]() is an upper bound for
is an upper bound for ![]() and
and ![]() is the smallest upper bound for
is the smallest upper bound for![]() ,
, ![]() Now we repeat the argument above with the roles of
Now we repeat the argument above with the roles of ![]() and
and ![]() reversed. We know that
reversed. We know that ![]() is the smallest number such that, for
is the smallest number such that, for
any ![]() Since
Since ![]() it follows that
it follows that ![]() for any
for any ![]() But
But ![]() Hence
Hence ![]() is an upper bound for
is an upper bound for![]() . But
. But ![]() is a supremum for
is a supremum for![]() . Hence
. Hence ![]() and
and ![]() We have shown that
We have shown that ![]() and also that
and also that ![]() Thus
Thus ![]()
2.3. Absorption Numbers in ![]()
One of standard ways of defining the completion of ![]() involves restricting oneself to subsets, which have the following property
involves restricting oneself to subsets, which have the following property ![]()
![]() . It is well known that in this case we obtain a field. In fact the proof is essentially the same as the one used in the case of ordinary Dedekind cuts in the development of the standard real numbers,
. It is well known that in this case we obtain a field. In fact the proof is essentially the same as the one used in the case of ordinary Dedekind cuts in the development of the standard real numbers, ![]() , of course, does not have the above property because no infinitesimal works.This suggests the introduction of the concept of absorption part
, of course, does not have the above property because no infinitesimal works.This suggests the introduction of the concept of absorption part ![]() of a number
of a number ![]() for an element
for an element ![]() of
of ![]() which, roughly speaking, measures how much
which, roughly speaking, measures how much ![]() departs from having the above property [7] .
departs from having the above property [7] .
Definition 2.9. [7] . Suppose ![]() then
then
![]() (2.17)
(2.17)
Example 2.5.
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
Lemma 2.9. [7] .
(i) ![]() and
and ![]()
(ii) ![]() and
and ![]()
Remark 2.9. By Lemma 2.7 ![]() may be regarded as an element of
may be regarded as an element of ![]() by adding on all negative elements of
by adding on all negative elements of ![]() to
to![]() . Of course if the condition
. Of course if the condition ![]() in the definition of
in the definition of ![]() is deleted we automatically get all the negative elements to be in
is deleted we automatically get all the negative elements to be in ![]() since
since ![]() The reason for our
The reason for our
definition is that the real interest lies in the non-negative numbers. A technicality occurs if![]() . We then identify
. We then identify ![]() with 0. [
with 0. [![]() becomes
becomes ![]() which by our early convention is not in
which by our early convention is not in![]() ].
].
Remark 2.10. By Lemma 2.7(ii), ![]() is additive idempotent.
is additive idempotent.
Lemma 2.10. [7] .
(i) ![]() is the maximum element
is the maximum element ![]() such that
such that ![]()
(ii) ![]() for
for ![]()
(iii) If ![]() is positive and idempotent then
is positive and idempotent then ![]()
Lemma 2.11. [7] . Let ![]() satsify
satsify ![]() Then the following are equivalent. In what follows assume
Then the following are equivalent. In what follows assume ![]()
(i) ![]() is idempotent,
is idempotent,
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]() for all finite
for all finite ![]()
Theorem 2.2. [7] . ![]()
Theorem 2.3. [7] . ![]()
Theorem 2.4. [7] .
(i) ![]()
(ii) ![]()
Theorem 2.5. [7] . Suppose ![]() then
then
(i) ![]()
(ii) ![]()
Theorem 2.6. [7] . Assume ![]() If
If ![]() absorbs
absorbs ![]() then
then ![]() absorbs
absorbs![]() .
.
Theorem 2.7. [7] . Let ![]() Then the following are equivalent
Then the following are equivalent
(i) ![]() is an idempotent,
is an idempotent,
(ii) ![]()
(iii) ![]()
(iv) Let ![]() and
and ![]() be two positive idempotents such that
be two positive idempotents such that ![]() Then
Then ![]()
2.4. Gonshor Types of a with Given ab.p.(a).
Among elements of ![]() such that
such that ![]() one can distinguish two many different types following [7] .
one can distinguish two many different types following [7] .
Definition 2.10. [7] . Assume ![]()
(i) ![]() has type 1 if
has type 1 if ![]()
(ii) ![]() has type 2 if
has type 2 if ![]() i.e.
i.e. ![]() has type 2 iff
has type 2 iff ![]() does not have type 1.
does not have type 1.
(iii) ![]() has type 1A if
has type 1A if ![]()
(iv) ![]() has type 2A if
has type 2A if ![]()
2.5. Robinson Part ![]() of Absorption Number
of Absorption Number ![]()
Theorem 2.8. [6] . Suppose ![]() Then there is a unique standard
Then there is a unique standard ![]() called Wattenberg stan- dard part of
called Wattenberg stan- dard part of ![]() and denoted by
and denoted by ![]() such that:
such that:
(i) ![]()
(ii) ![]() implies
implies ![]()
(iii) The map ![]() is continuous.
is continuous.
(iv) ![]()
(v) ![]()
(vi) ![]()
(vii) ![]() if
if ![]()
Theorem 2.9. [7] .
(i) ![]() has type 1 iff
has type 1 iff ![]() has type 1A,
has type 1A,
(ii) ![]() cannot have type 1 and type 1A simultaneously.
cannot have type 1 and type 1A simultaneously.
(iii) Suppose ![]() Then
Then ![]() has type 1 iff
has type 1 iff ![]() has the form
has the form ![]() for some
for some![]() .
.
(iv) Suppose![]() .
. ![]() has type 1A iff
has type 1A iff ![]() has the form
has the form ![]() for some
for some![]() .
.
(v) If ![]() then
then ![]() has type 1 iff
has type 1 iff ![]() has type 1.
has type 1.
(vi) If ![]() then
then ![]() has type 2 iff either
has type 2 iff either ![]() or
or ![]() has type 2.
has type 2.
Proof (iii) Let ![]() Then
Then![]() . Since
. Since ![]() (we chose
(we chose ![]() such that
such that ![]() and write
and write ![]() as
as![]() ).
).
It is clear that ![]() works to show that
works to show that ![]() has type 1.
has type 1.
Conversely, suppose ![]() has type 1 and choose
has type 1 and choose ![]() such that:
such that: ![]() Then we claim that:
Then we claim that: ![]()
By definition of ![]() certainly
certainly![]() . On the other hand by choice of
. On the other hand by choice of![]() , every element of
, every element of ![]() has the form
has the form ![]() with
with![]() .
.
Choose ![]() such that
such that ![]() then
then![]() .
.
Hence ![]() Therefore
Therefore ![]()
Examples.
(i) ![]() has type 1 and therefore
has type 1 and therefore ![]() has type 1A. Note that also
has type 1A. Note that also ![]() has type 2. (ii) Suppose
has type 2. (ii) Suppose ![]() Then
Then ![]() has type 1 and therefore
has type 1 and therefore ![]() has type 1A.
has type 1A.
(ii) Suppose ![]() i.e.
i.e. ![]() has type 1 and therefore by Theorem 2.9
has type 1 and therefore by Theorem 2.9 ![]() has the form
has the form ![]() for some unique
for some unique ![]() Then, we define unique Robinson part
Then, we define unique Robinson part ![]() of absor- ption number
of absor- ption number ![]() by formula
by formula
![]() (2.18)
(2.18)
(iii) Suppose ![]() i.e.
i.e. ![]() has type 1A and therefore by Theorem 2.9
has type 1A and therefore by Theorem 2.9 ![]() has the form
has the form ![]() for some unique
for some unique ![]() Then we define unique. Robinson part
Then we define unique. Robinson part ![]() of absorption number
of absorption number ![]() by formula
by formula
![]() (2.19)
(2.19)
(iv) Suppose ![]() and
and ![]() has type 1A, i.e.
has type 1A, i.e. ![]() has the form
has the form ![]() for some
for some ![]() Then, we define Robinson part
Then, we define Robinson part ![]() of absorption number
of absorption number ![]() by formula
by formula
![]() (2.20)
(2.20)
(v) Suppose ![]() and
and ![]() has type 1A, i.e.
has type 1A, i.e. ![]() has the form
has the form ![]() for some
for some ![]() Then, we define Robinson part
Then, we define Robinson part ![]() of absorption number
of absorption number ![]() by formula
by formula
![]() (2.21)
(2.21)
Remark 2.11. Note that in general case, i.e. if ![]() Robinson part
Robinson part ![]() of absorption number
of absorption number ![]() is not unique.
is not unique.
Remark 2.12. Suppose ![]() and
and ![]() has type 1 or type 1A. Then by definitions above one obtains the representation
has type 1 or type 1A. Then by definitions above one obtains the representation
![]()
2.6. The Pseudo-Ring of Wattenberg Hyperintegers ![]()
Lemma 2.12. [6] . Suppose that ![]() Then the following two conditions on
Then the following two conditions on ![]() are equivalent:
are equivalent:
(i) ![]()
(ii) ![]()
Definition 2.11. [6] . If ![]() satisfies the conditions mentioned above
satisfies the conditions mentioned above ![]() is said to be the Wattenberg hyperinteger. The set of all Wattenberg hyperintegers is denoted by
is said to be the Wattenberg hyperinteger. The set of all Wattenberg hyperintegers is denoted by ![]()
Lemma 2.13. [6] . Suppose ![]() Then
Then
(i) ![]()
(ii) ![]()
(iii) ![]()
The set of all positive Wattenberg hyperintegers is called the Wattenberg hypernaturals and is denoted by ![]()
Definition 2.12. Suppose that (i) ![]() (ii)
(ii) ![]() and (iii)
and (iii) ![]()
If ![]() and
and ![]() satisfies these conditions then we say that
satisfies these conditions then we say that ![]() is divisible by
is divisible by ![]() and we denote this by
and we denote this by ![]()
Definition 2.13. Suppose that (i) ![]() and (ii) there exists
and (ii) there exists ![]() such that
such that
(1) ![]() or
or
(2) ![]()
If ![]() satisfies the conditions mentioned above then we say that
satisfies the conditions mentioned above then we say that ![]() is divisible by
is divisible by ![]() and we denote this by
and we denote this by![]() .
.
Theorem 2.10. (i) Let ![]()
![]() be a prime hypernaturals such that (i)
be a prime hypernaturals such that (i)![]() . Let
. Let ![]() be a Wattenberg hypernatural such that (i)
be a Wattenberg hypernatural such that (i)![]() . Then
. Then ![]()
(ii) ![]() has type 1 iff
has type 1 iff ![]() has type 1A,
has type 1A,
(iii) ![]() cannot have type 1 and type 1A simultaneously.
cannot have type 1 and type 1A simultaneously.
(iv) Suppose ![]() Then
Then ![]() has type 1 iff
has type 1 iff ![]() has the form
has the form ![]() for some
for some ![]()
(v) Suppose ![]()
![]()
![]() has type 1A iff
has type 1A iff ![]() has the form
has the form ![]() for some
for some ![]()
(vi) Suppose ![]() If
If ![]() then
then ![]() has type 1 iff
has type 1 iff ![]() has type 1.
has type 1.
(vii) Suppose ![]() If
If ![]() then
then ![]() has type 2 iff either
has type 2 iff either ![]() or
or ![]() has type 2.
has type 2.
Proof. (i) Immediately follows from definitions (2.12)-(2.13).
(iv) Let ![]() Then
Then![]() . Since
. Since ![]() (we chose
(we chose ![]() such that
such that ![]() and write a as
and write a as![]() ).
).
It is clear that a works to show that ![]() has type 1.
has type 1.
Conversely, suppose ![]() has type
has type ![]() and choose
and choose ![]() such that:
such that: ![]() Then we claim that:
Then we claim that: ![]()
By definition of ![]() certainly
certainly![]() . On the other hand by choice of a, every element of
. On the other hand by choice of a, every element of ![]() has the form
has the form ![]() with
with![]() .
.
Choose ![]() such that
such that ![]() then
then![]() .
.
Hence ![]() Therefore
Therefore ![]()
2.7. The Integer Part Int.p(a) of Wattenberg Hyperreals ![]()
Definition 2.14. Suppose ![]() Then, we define
Then, we define ![]() by formula
by formula
![]()
Obviously there are two possibilities:
1. A set ![]() has no greatest element. In this case valid only the
has no greatest element. In this case valid only the
Property I: ![]()
Since ![]() implies
implies ![]() such that
such that ![]() But then
But then ![]() which implies
which implies ![]() contradicting
contradicting ![]()
2. A set ![]() has a greatest element,
has a greatest element, ![]() In this case valid the
In this case valid the
Property II: ![]() and obviously
and obviously ![]()
Definition 2.15. Suppose ![]() Then, we define
Then, we define ![]() by formula
by formula
![]()
Note that obviously: ![]()
2.8. External Sum of the Countable Infinite Series in ![]()
This subsection contains key definitions and properties of summ of countable sequence of Wattenberg hyperreals.
Definition 2. 16. [4] . Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that
(i) ![]() or (ii)
or (ii) ![]() or
or
(iii) ![]()
![]()
Then external sum (#-sum) ![]() of the corresponding countable sequence
of the corresponding countable sequence ![]() is defined by
is defined by
![]() (2.22)
(2.22)
Theorem 2.11. (i) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that ![]() and
and ![]() Then
Then![]() .
.
(ii) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that ![]() and
and ![]() Then
Then![]() .
.
(iii) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that ![]()
![]() and infinite series
and infinite series ![]() absolutely converges to
absolutely converges to ![]() in
in ![]() Then
Then
![]() (2.23)
(2.23)
(iv) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that ![]()
![]() and infinite series
and infinite series![]() absolutely converges to
absolutely converges to ![]() in
in ![]() Then
Then
![]() (2.24)
(2.24)
(v) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that
(1) ![]()
![]() and
and
(2) ![]()
Then
![]() (2.25)
(2.25)
Proof. (i) Let ![]() and
and ![]() Then obviously:
Then obviously: ![]()
Thus ![]() there exists
there exists ![]() such that (1)
such that (1)
(1) ![]()
Therefore from (1) by Robinson transfer one obtains (2)
(2)![]()
Using now Wattenberg embedding from (2) we obtain (3)
(3) ![]()
From (3) one obtains (4)
(4) ![]()
Note that ![]() obviously
obviously ![]()
(5) ![]()
From (4) and (5) one obtains (6)
(6) ![]()
Thus (i) immediately from (6) and from definition of the idempotent![]() .
.
Proof.(ii) Immediately from (i) by Lemma 2.3 (v).
Proof.(iii) Let![]() . Then obviously:
. Then obviously: ![]() and
and![]() . Thus
. Thus ![]() there exists
there exists ![]() such that (1)
such that (1)
(1) ![]()
Therefore from (1) by Robinson transfer one obtains (2)
(2) ![]()
Using now Wattenberg embedding from (2) we obtain (3)
(3) ![]()
From (3) one obtains (4)
(4) ![]()
From (4) by Definition 2.16 (i) one obtains
(5) ![]()
Note that ![]() obviously
obviously
(6) ![]()
From (5)-(6) follows (7)
(7) ![]()
Thus Equation (2.23) immediately from (7) and from definition of the idempotent![]() .
.
Proof.(iv) Immediately from (iii) by Lemma 2.3 (v).
Proof.(v) From Definition 2.16.(iii) and Equation (2.23)-Equation (2.24) by Theorem 2.7.(iii) one obtains
![]()
Theorem 2.12. Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in![]() . Let
. Let ![]() be external sum of the corresponding countable sequence
be external sum of the corresponding countable sequence![]() . Let
. Let ![]() be a countable sequence where
be a countable sequence where ![]() is any rearrangement of terms of the sequence
is any rearrangement of terms of the sequence![]() . Then external sum
. Then external sum ![]() of the corresponding countable sequence
of the corresponding countable sequence ![]() has the same value s as external sum of the countable sequence
has the same value s as external sum of the countable sequence![]() , i.e.
, i.e. ![]()
Theorem 2.13. (i) Let ![]() be a countable sequence
be a countable sequence ![]() such that (1)
such that (1) ![]() (2) infinite series
(2) infinite series ![]() absolutely converges to
absolutely converges to ![]() in
in ![]() and let
and let ![]() be external sum of the corresponding sequence
be external sum of the corresponding sequence![]() . Then for any
. Then for any ![]() the equality is satisfied
the equality is satisfied
![]() (2.26)
(2.26)
(ii) Let ![]() be a countable sequence
be a countable sequence ![]() such that (1)
such that (1) ![]() (2) infinite series
(2) infinite series ![]() absolutely converges to
absolutely converges to ![]() in
in ![]() and let
and let ![]() be external sum of the corresponding sequence
be external sum of the corresponding sequence![]() . Then for any
. Then for any ![]() the equality is satisfied:
the equality is satisfied:
![]() (2.27)
(2.27)
(iii) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that
(1) ![]()
![]()
(2) infinite series ![]() absolutely converges to
absolutely converges to ![]() in
in![]() ,
,
(3) infinite series ![]() absolutely converges to
absolutely converges to ![]() in
in![]() .
.
Then the equality is satisfied:
![]() (2.28)
(2.28)
Proof. (i) From Definition 2.16. (i) by Theorem 2.1, Theorem 2.11. (i) and Lemma (2.4) (ii) one obtains
![]()
(ii) Straightforward from Definition 2.16. (i) and Theorem 2.1, Theorem 2.11. (ii) and Lemma (2.4) (ii) one obtains
![]()
(iii) By Theorem 2.11. (iii) and Lemma (2.4). (ii) one obtains
![]()
But other side from (i) and (ii) follows
![]()
Definition 2.17. Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() We assume now that:
We assume now that:
(i) there exists ![]() such that
such that ![]() or
or
(ii) there exists ![]() such that
such that ![]() or
or
(iii) there exists infinite sequence ![]() such that
such that
(a) ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() and
and
(b) there exists infinite sequence ![]() such that
such that ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to![]() .
.
Then: (i) external upper sum (#-upper sum) of the corresponding countable sequence ![]() is defined by
is defined by
![]() (2.29)
(2.29)
(ii) external lower sum (#-lower sum) of the corresponding countable sequence ![]() is defined by
is defined by
![]() (2.30)
(2.30)
Theorem 2.14. (1) Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() We assume now that:
We assume now that:
(i) there exists ![]() such that
such that ![]() or
or
(ii) there exists ![]() such that
such that ![]() or
or
(iii) there exists infinite sequence ![]() such that
such that
(a) ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() and
and
(b) there exists infinite sequence ![]() such that
such that ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to![]() .
.
Then
![]() (2.31)
(2.31)
and
![]() (2.32)
(2.32)
Proof. (i), (ii), (iii) straightforward from definitions.
Theorem 2.15. (1) Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() We assume now that:
We assume now that:
(i) there exists ![]() such that
such that ![]() or
or
(ii) there exists ![]() such that
such that ![]() or
or
(iii) there exists infinite sequence ![]() such that
such that
(a) ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() and
and
(b) there exists infinite sequence ![]() such that
such that ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to![]() .
.
Then for any ![]() the equalities is satisfied
the equalities is satisfied
![]() (2.33)
(2.33)
and
![]() (2.34)
(2.34)
Proof. Copy the proof of the Theorem 2.13.
Theorem 2.16. (1) Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() We assume now that:
We assume now that:
(i) there exists ![]() such that
such that ![]() or
or
(ii) there exists ![]() such that
such that ![]() or
or
(iii) there exists infinite sequence ![]() such that
such that
(a) ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() and
and
(b) there exists infinite sequence ![]() such that
such that ![]() and infinite series
and infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]()
Then for any ![]() the equalities is satisfied
the equalities is satisfied
![]() (2.35)
(2.35)
and
![]() (2.36)
(2.36)
Proof. (1) From Equation (2.31) we obtain
![]() (2.37)
(2.37)
From Equation (2.37) by Theorem 2.1 we obtain directly
![]() (2.38)
(2.38)
(2) From Equation (2.32) we obtain
![]() (2.39)
(2.39)
From Equation (2.39) by Theorem 2.1 we obtain directly
![]() (2.40)
(2.40)
Remark 2.13. Note that we have proved Equation (2.35) and Equation (2.36) without any reference to the Lemma 2.4.
Definition 2.18. (i) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that
![]() (2.41)
(2.41)
Then external countable upper sum (#-sum) of the countable sequence ![]() is defined by
is defined by
![]() (2.42)
(2.42)
In particular if ![]() where
where ![]() the external countable upper sum (#-sum) of the countable sequence
the external countable upper sum (#-sum) of the countable sequence ![]() is defined by
is defined by
![]() (2.43)
(2.43)
(ii) Let ![]() be a countable sequence
be a countable sequence ![]() such that
such that
![]() (2.44)
(2.44)
Then external countable lower sum (#-sum) of the countable sequence ![]() is defined by
is defined by
![]() (2.45)
(2.45)
In particular if ![]() where
where ![]() the external countable lower sum (#-sum) of the countable sequence
the external countable lower sum (#-sum) of the countable sequence ![]() is defined by
is defined by
![]() (2.46)
(2.46)
Theorem 2.17. (i) Let ![]() be a countable sequence
be a countable sequence ![]() such that valid the property (2.41). Then for any
such that valid the property (2.41). Then for any ![]() the equality is satisfied
the equality is satisfied
![]() (2.47)
(2.47)
(ii) Let ![]() be a countable sequence
be a countable sequence ![]() such that valid the property (2.44).
such that valid the property (2.44).
Then for any ![]() the equality is satisfied
the equality is satisfied
![]() (2.48)
(2.48)
Proof. Immediately from Definition 2.18 by Theorem 2.1.
Definition 2.19. Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in![]() . Then external countable complex sum (#-sum) of the corresponding countable sequence
. Then external countable complex sum (#-sum) of the corresponding countable sequence ![]() is defined by
is defined by
![]() (2.49)
(2.49)
correspondingly.
Note that any properties of this sum immediately follow from the properties of the real external sum.
Definition 2.20. (i) We define now Wattenberg complex plane ![]() by
by ![]() with
with![]() . Thus for any
. Thus for any ![]() we obtain
we obtain![]() , where
, where![]() , (ii) for any
, (ii) for any ![]() such that
such that ![]() we define
we define ![]() by
by![]() .
.
Theorem 2.18. Let ![]() be a countable sequence
be a countable sequence ![]() such that infinite series
such that infinite series ![]() absolutely converges in
absolutely converges in ![]() to
to ![]() and
and![]() . Then
. Then
(i) ![]()
(ii) ![]()
2.9. Gonshor Transfer
Definition 2.21. [7] . Let![]() .
.
Note that ![]() satisfies the usual axioms for a closure operator,i.e. if (i)
satisfies the usual axioms for a closure operator,i.e. if (i) ![]() and
and
(ii) S has no maximum, then ![]()
Let f be a continuous strictly increasing function in each variable from a subset of ![]() into
into![]() . Specifically, we want the domain to be the cartesian product
. Specifically, we want the domain to be the cartesian product ![]() where
where ![]() for some
for some ![]() By Robin- son transfer f extends to a function
By Robin- son transfer f extends to a function ![]() from the corresponding subset of
from the corresponding subset of ![]() into
into ![]() which is also strictly increasing in each variable and continuous in the Q topology (i.e.
which is also strictly increasing in each variable and continuous in the Q topology (i.e. ![]() and
and ![]() range over arbitrary positive elements in
range over arbitrary positive elements in![]() ). We now extend
). We now extend ![]() to
to ![]()
![]() (2.50)
(2.50)
Definition 2.22. [7] . Let ![]()
![]()
![]() then
then
![]() (2.51)
(2.51)
Theorem 2.19. [7] . If f and g are functions of one variable then
![]() (2.52)
(2.52)
Theorem 2.20. [7] . Let f be a function of two variables. Then for any ![]() and
and ![]()
![]() (2.53)
(2.53)
Theorem 2.21. [7] . Let f and g be any two terms obtained by compositions of strictly increasing continuous functions possibly containing parameters in![]() . Then any relation
. Then any relation ![]() or
or ![]() valid in
valid in ![]() extends to
extends to ![]() i.e.
i.e.
![]() (2.54)
(2.54)
Remark 2.14. For any function ![]() we often write for short
we often write for short ![]() instead of
instead of![]() .
.
Theorem 2.22. [7] . (1) For any ![]()
![]() (2.55)
(2.55)
For any ![]()
![]() (2.56)
(2.56)
(2) For any ![]()
![]() (2.57)
(2.57)
(3) For any ![]()
![]() (2.58)
(2.58)
(4) For any ![]()
![]() (2.59)
(2.59)
Note that we must always beware of the restriction in the domain when it comes to multiplication.
Theorem 2.23. [7] . The map ![]() maps the set of additive idempotents onto the set of all multiplicative idempotents other than 0.
maps the set of additive idempotents onto the set of all multiplicative idempotents other than 0.
3. The Proof of the #-Transcendene of the Numbers ![]()
In this section we will prove the #-transcendence of the numbers ![]() Key idea of this proof reduction of the statement of
Key idea of this proof reduction of the statement of ![]() is #-transcendental number to equivalent statement in
is #-transcendental number to equivalent statement in ![]() by using pseudoring of Wattenberg hyperreals
by using pseudoring of Wattenberg hyperreals ![]() [6] and Gonshor idempotent theory [7] . We obtain this reduction by three steps, see Subsections 3.2.1 - 3.2.3.
[6] and Gonshor idempotent theory [7] . We obtain this reduction by three steps, see Subsections 3.2.1 - 3.2.3.
3.1. The Basic Definitions of the Shidlovsky Quantities
In this section we remind the basic definitions of the Shidlovsky quantities [8] . Let ![]() and
and ![]() be the Shidlovsky quantities:
be the Shidlovsky quantities:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
where ![]() this is any prime number. Using Equations (3.1)-(3.3.) by simple calculation one obtains:
this is any prime number. Using Equations (3.1)-(3.3.) by simple calculation one obtains:
![]() (3.4)
(3.4)
and consequently
![]() (3.5)
(3.5)
Lemma 3.1. [8] . Let p be a prime number. Then ![]()
Proof. ([8] , p. 128) By simple calculation one obtains the equality
![]() (3.6)
(3.6)
where p is a prime. By using equality ![]() where
where ![]() from Equations (3.1) and (3.6) one obtains
from Equations (3.1) and (3.6) one obtains
![]() (3.7)
(3.7)
Thus
![]() (3.8)
(3.8)
Lemma 3.2. [8] . Let p be a prime number. Then ![]()
![]()
![]() .
.
Proof. ([8] , p. 128) By subsitution ![]() from Equation (3.3) one obtains
from Equation (3.3) one obtains
![]() (3.9)
(3.9)
By using equality
![]() (3.10)
(3.10)
and by subsitution Equation (3.10) into RHS of the Equation (3.9) one obtains
![]() (3.11)
(3.11)
Lemma 3.3. [8] . (i) There exists sequences ![]() and
and ![]() such that
such that
![]() (3.12)
(3.12)
where sequences ![]() and
and ![]() does not depend on number p. (ii) For any
does not depend on number p. (ii) For any ![]() if
if![]() .
.
Proof. ([8] , p. 129) Obviously there exists sequences ![]() and
and ![]() such that
such that ![]() and
and ![]() does not depend on number p
does not depend on number p
![]() (3.13)
(3.13)
and
![]() (3.14)
(3.14)
Substitution inequalities (3.13)-(3.14) into RHS of the Equation (3.3) by simple calculation gives
![]() (3.15)
(3.15)
Statement (i) follows from (3.15). Statement (ii) immediately follows from a statement (ii).
Lemma 3.4. [8] . For any ![]() and for any
and for any ![]() such that
such that ![]() there exists
there exists ![]() such that
such that
![]() (3.16)
(3.16)
Proof. From Equation (3.5) one obtains
![]() (3.17)
(3.17)
From Equation (3.17) by using Lemma 3.3. (ii) one obtains (3.17).
Remark 3.1. We remind now the proof of the transcendence of ![]() following Shidlovsky proof is given in his book [8] .
following Shidlovsky proof is given in his book [8] .
Theorem 3.1. The number ![]() is transcendental.
is transcendental.
Proof. ([8] , pp. 126-129) Suppose now that ![]() is an algebraic number; then it satisfies some relation of the form
is an algebraic number; then it satisfies some relation of the form
![]() (3.18)
(3.18)
where ![]() integers and where
integers and where ![]() Having substituted RHS of the Equation (3.5) into Equation (3.18) one obtains
Having substituted RHS of the Equation (3.5) into Equation (3.18) one obtains
![]() (3.19)
(3.19)
From Equation (3.19) one obtains
![]() (3.20)
(3.20)
We rewrite the Equation (3.20) for short in the form
![]() (3.21)
(3.21)
We choose now the integers ![]() such that:
such that:
![]() (3.22)
(3.22)
and![]() . Note that
. Note that ![]() Thus one obtains
Thus one obtains
![]() (3.23)
(3.23)
and therefore
![]() (3.24)
(3.24)
By using Lemma 3.4 for any ![]() such that
such that ![]() we can choose a prime number
we can choose a prime number ![]() such that:
such that:
![]() (3.25)
(3.25)
From (3.25) and Equation (3.21) we obtain
![]() (3.26)
(3.26)
From (3.26) and Equation (3.24) one obtains the contradiction.This contradiction finalized the proof.
3.2. The Proof of the #-Transcendene of the Numbers![]() . We Will Divide the Proof into Four Parts
. We Will Divide the Proof into Four Parts
3.2.1. Part I. The Robinson Transfer of the Shidlovsky Quantities ![]()
In this subsection we will replace using Robinson transfer the Shidlovsky quantities ![]() by corresponding nonstandard quantities
by corresponding nonstandard quantities ![]()
![]() The properties of the nonstandard quantities
The properties of the nonstandard quantities ![]() one obtains directly from the pro-
one obtains directly from the pro-
perties of the standard quantities ![]() using Robinson transfer principle [4] [5] .
using Robinson transfer principle [4] [5] .
1. Using Robinson transfer principle [4] [5] from Equation (3.8) one obtains directly
![]() (3.27)
(3.27)
From Equation (3.11) using Robinson transfer principle one obtains![]() :
:
![]() (3.28)
(3.28)
Using Robinson transfer principle from inequality (3.15) one obtains![]() :
:
![]() (3.29)
(3.29)
Using Robinson transfer principle, from Equation (3.5) one obtains![]() :
:
![]() (3.30)
(3.30)
Lemma 3.5. Let![]() , then for any
, then for any ![]() and for any
and for any ![]() there exists
there exists ![]() such that
such that
![]() (3.31)
(3.31)
Proof. From Equation (3.30) we obtain![]() :
:
![]() (3.32)
(3.32)
From Equation (3.32) and (3.29) we obtain (3.31).
3.2.2. Part II. The Wattenberg Imbedding ![]() into
into ![]()
In this subsection we will replace by using Wattenberg imbedding [6] and Gonshor transfer the nonstandard quantities ![]() and the nonstandard Shidlovsky quantities
and the nonstandard Shidlovsky quantities ![]()
![]() by correspond- ing Wattenberg quantities
by correspond- ing Wattenberg quantities ![]() The properties of the Wattenberg quantities
The properties of the Wattenberg quantities ![]() one obtains directly from the properties of the co- rresponding nonstandard quantities
one obtains directly from the properties of the co- rresponding nonstandard quantities ![]() using Gonshor transfer principle [4] [7] .
using Gonshor transfer principle [4] [7] .
1. By using Wattenberg imbedding ![]() from Equation (3.30) one obtains
from Equation (3.30) one obtains
![]() (3.33)
(3.33)
2. By using Wattenberg imbedding ![]() and Gonshor transfer (see Subsection 2.9 Theorem 2.19) from Equation (3.27) one obtains
and Gonshor transfer (see Subsection 2.9 Theorem 2.19) from Equation (3.27) one obtains
![]() (3.34)
(3.34)
3. By using Wattenberg imbedding ![]() from Equation (3.28) one obtains
from Equation (3.28) one obtains
![]() (3.35)
(3.35)
Lemma 3.6. Let ![]() then for any
then for any ![]() and for any
and for any ![]() there exists
there exists ![]() such that
such that
![]() (3.36)
(3.36)
Proof. Inequality (3.36) immediately follows from inequality (3.31) by using Wattenberg imbedding ![]() and Gonshor transfer.
and Gonshor transfer.
3.2.3. Part III. Reduction of the Statement of e Is #-Transcendental Number to Equivalent Statement in ![]() Using Gonshor Idempotent Theory
Using Gonshor Idempotent Theory
To prove that ![]() is #-transcendental number we must show that e is not w-transcendental, i.e., there does not exist real
is #-transcendental number we must show that e is not w-transcendental, i.e., there does not exist real ![]() -analytic function
-analytic function ![]() with rational coefficients
with rational coefficients ![]() such that
such that
![]() (3.37)
(3.37)
Suppose that e is w-transcendental, i.e., there exists an ![]() -analytic function
-analytic function ![]() with rational coefficients:
with rational coefficients:
![]() (3.38)
(3.38)
such that the equality is satisfied:
![]() (3.39)
(3.39)
In this subsection we obtain an reduction of the equality given by Equation (3.39) to equivalent equality given by Equation (3). The main tool of such reduction that external countable sum defined in Subsection 2.8.
Lemma 3.7. Let ![]() and
and ![]() be the sum correspondingly
be the sum correspondingly
![]() (3.40)
(3.40)
Then ![]()
Proof. Suppose there exists k such that ![]() Then from Equation (3.39) follows
Then from Equation (3.39) follows ![]() There- fore by Theorem 3.1 one obtains the contradiction.
There- fore by Theorem 3.1 one obtains the contradiction.
Remark 3.2. Note that from Equation (3.39) follows that in generel case there is a sequence ![]() such that
such that
![]() (3.41)
(3.41)
or there is a sequence ![]() such that
such that
![]() (3.42)
(3.42)
or both sequences ![]() and
and ![]() with a property that is specified above exist.
with a property that is specified above exist.
Remark 3.3. We assume now for short but without loss of generelity that (3.41) is satisfied. Then from (3.41) by using Definition 2.17 and Theorem 2.14 (see Subsection 2.8) one obtains the equality [4]
![]() (3.43)
(3.43)
Remark 3.4. Let ![]() and
and ![]() be the upper external sum defined by
be the upper external sum defined by
![]() (3.44)
(3.44)
Note that from Equation (3.43)-Equation (3.44) follows that
![]() (3.45)
(3.45)
Remark 3.5. Assume that ![]() and
and![]() . In this subsection we will write for a short
. In this subsection we will write for a short ![]() iff
iff ![]() absorbs
absorbs![]() , i.e.
, i.e. ![]()
Lemma 3.8. ![]()
Proof. Suppose there exists ![]() such that
such that ![]() Then from Equation(3.45) one obtains
Then from Equation(3.45) one obtains
![]() (3.46)
(3.46)
From Equation (3.46) by Theorem 2.11 follows that ![]() and therefore by Lemma 3.7 one obtains the contradiction.
and therefore by Lemma 3.7 one obtains the contradiction.
Theorem 3.2. [4] The equality (3.43) is inconsistent.
Proof. Let us consider hypernatural number ![]() defined by countable sequence
defined by countable sequence
![]() (3.47)
(3.47)
From Equation (3.43) and Equation (3.47) one obtains
![]() (3.48)
(3.48)
Remark 3.6. Note that from inequality (3.27) by Wattenberg transfer one obtains
![]() (3.49)
(3.49)
Substitution Equation (3.30) into Equation (3.48) gives
![]() (3.50)
(3.50)
Multiplying Equation (3.50) by Wattenberg hyperinteger ![]() by Theorem 2.13 (see subsec- tion 2.8) one obtains
by Theorem 2.13 (see subsec- tion 2.8) one obtains
![]() (3.51)
(3.51)
By using inequality (3.49) for a given ![]()
![]() we will choose infinite prime integer
we will choose infinite prime integer ![]() such that:
such that:
![]() (3.52)
(3.52)
Now using the inequality (3.49) we are free to choose a prime hyperinteger ![]() and
and ![]()
![]() in the Equation (3.51) for a given
in the Equation (3.51) for a given ![]() such that:
such that:
![]() (3.53)
(3.53)
Hence from Equation (3.52) and Equation (3.53) we obtain
![]() (3.54)
(3.54)
Therefore from Equations (3.51) and (3.54) by using definition (2.15) of the function ![]() given by Equation (2.20)-Equation (2.21) and corresponding basic property I (see Subsection 2.7) of the function
given by Equation (2.20)-Equation (2.21) and corresponding basic property I (see Subsection 2.7) of the function ![]() we obtain
we obtain
![]() (3.55)
(3.55)
From Equation (3.55) using basic property I of the function ![]() finally we obtain the main equality
finally we obtain the main equality
![]() (3.56)
(3.56)
We will choose now infinite prime integer ![]() in Equation (3.56)
in Equation (3.56) ![]() such that
such that
![]() (3.57)
(3.57)
Hence from Equation (3.34) follows
![]() (3.58)
(3.58)
Note that ![]() Using (3.57) and (3.58) one obtains:
Using (3.57) and (3.58) one obtains:
![]() (3.59)
(3.59)
Using Equation(3.35) one obtains
![]() (3.60)
(3.60)
3.2.4. Part IV. The Proof of the Inconsistency of the Main Equality (3.56)
In this subsection we wil prove that main equality (3.56) is inconsistent. This prooff based on the Theorem 2.10 (v), see Subsection 2.6.
Lemma 3.9. The equality (3.56) under conditions (3.59)-(3.60) is inconsistent.
Proof. (I) Let us rewrite Equation (3.56) in the short form
![]() (3.61)
(3.61)
where
![]() (3.62)
(3.62)
From (3.59)-(3.60) follows that
![]() (3.63)
(3.63)
Remark 3.7. Note that ![]() Otherwise we obtain that
Otherwise we obtain that ![]() But the other hand from Equation (3.61) follows that
But the other hand from Equation (3.61) follows that ![]() But this is a contradic- tion. This contradiction completed the proof of the statement (I).
But this is a contradic- tion. This contradiction completed the proof of the statement (I).
(II) Let ![]() and
and ![]() be the external sum correspondingly
be the external sum correspondingly
![]() (3.64)
(3.64)
Note that from Equation (3.61) and Equation (3.64) follows that
![]() (3.65)
(3.65)
Lemma 3.10. Under conditions (3.59)-(3.60)
![]() (3.66)
(3.66)
and
![]() (3.67)
(3.67)
Proof. First note that under conditions (3.59)-(3.60) one obtains
![]() (3.68)
(3.68)
Suppose that there exists an ![]() such that
such that ![]() Then from Equation (3.65) one obtains
Then from Equation (3.65) one obtains
![]() (3.69)
(3.69)
From Equation (3.69) by Theorem 2.17 one obtains
![]() (3.70)
(3.70)
Thus
![]() (3.71)
(3.71)
From Equation (3.71) by Theorem 2.11 follows that ![]() and therefore by Lemma 3.7 one obtains the contradiction. This contradiction finalized the proof of the Lemma 3.10.
and therefore by Lemma 3.7 one obtains the contradiction. This contradiction finalized the proof of the Lemma 3.10.
Part (III)
Remark 3.8. (i) Note that from Equation (3.62) by Theorem 2.10 (v) follws that ![]() has the form
has the form
![]() (3.72)
(3.72)
where
![]() (3.73)
(3.73)
(ii) Substitution by Equation (3.72) into Equation (3.61) gives
![]() (3.74)
(3.74)
Remark 3.9. Note that from (3.74) by definitions follows that
![]() (3.75)
(3.75)
Remark 3.10. Note that from (3.73) by construction of the Wattenberg integer ![]() obviously follows that there exists some
obviously follows that there exists some ![]() such that
such that
![]() (3.76)
(3.76)
Therefore
![]() (3.77)
(3.77)
Note that under conditions (3.59)-(3.60) and (3.73) obviously one obtains
![]() (3.78)
(3.78)
From Equation(3.74) follows that
![]() (3.79)
(3.79)
Therefore
![]() (3.80)
(3.80)
From (3.78) follows that
![]() (3.81)
(3.81)
Note that by Theorem 2.8 (see Subsection 2.5) and Formula (3.44) one otains
![]() (3.82)
(3.82)
From Equation (3.81)-Equation (3.82) follows that
![]() (3.83)
(3.83)
Thus
![]() (3.84)
(3.84)
and therefore
![]() (3.85)
(3.85)
But this is a contradiction. This contradiction completed the proof of the Lemma 3.9.
4. Generalized Shidlovsky Quantities
In this section we remind the basic definitions of the Shidlovsky quantities, see [8] pp. 132-134.
Theorem 4.1. [8] Let ![]() be a polynomials with coefficients in
be a polynomials with coefficients in![]() . Assume that for any
. Assume that for any ![]() algebraic numbers over the field
algebraic numbers over the field ![]()
![]() form a complete set of the roots of
form a complete set of the roots of ![]() such that
such that
![]() (4.1)
(4.1)
and ![]() Then:
Then:
![]() (4.2)
(4.2)
Let ![]() be a polynomial such that
be a polynomial such that
![]() (4.3)
(4.3)
Let ![]() and
and ![]() be the quantities [8] :
be the quantities [8] :
![]() (4.4)
(4.4)
where in (4.4) we integrate in complex plane ![]() along line
along line ![]() see Picture 1 .
see Picture 1 .
![]() (4.5)
(4.5)
where ![]() and where in (4.5) we integrate in complex plane
and where in (4.5) we integrate in complex plane ![]() along line with initial point
along line with initial point ![]() and which are parallel to real axis of the complex plane
and which are parallel to real axis of the complex plane![]() , see Picture 1 .
, see Picture 1 .
![]() (4.6)
(4.6)
where ![]() and where in (4.6) we integrate in complex plane
and where in (4.6) we integrate in complex plane ![]() along contour
along contour ![]() see Picture 1 .
see Picture 1 .
From Equation (4.3) one obtains
![]() (4.7)
(4.7)
where ![]() Now from Equation (4.4) and Equation (4.7) using formula
Now from Equation (4.4) and Equation (4.7) using formula
![]()
![]()
Picture 1. Contour ![]() in complex plane
in complex plane![]() .
.
one obtains
![]() (4.8)
(4.8)
where ![]() We choose now a prime p such that
We choose now a prime p such that ![]() Then from Equation (4.8) follows that
Then from Equation (4.8) follows that
![]() (4.9)
(4.9)
From Equation (4.3) and Equation (4.5) one obtains
![]() (4.10)
(4.10)
where ![]() By change of the variable integration
By change of the variable integration ![]() in RHS of the Equation (4.10) we obtain
in RHS of the Equation (4.10) we obtain
![]() (4.11)
(4.11)
where ![]() Let us rewrite now Equation (4.11) in the following form
Let us rewrite now Equation (4.11) in the following form
![]() (4.12)
(4.12)
Let ![]() be a ring of the all algebraic integers. Note that [8]
be a ring of the all algebraic integers. Note that [8]
![]() (4.13)
(4.13)
Let us rewrite now Equation (4.12) in the following form
![]() (4.14)
(4.14)
where ![]() From Equation (4.14) one obtains
From Equation (4.14) one obtains
![]() (4.15)
(4.15)
The polinomial ![]() is a symmetric polynomial on any system
is a symmetric polynomial on any system ![]() of variables
of variables ![]() where
where
![]() (4.16)
(4.16)
It well known that ![]() [8] and therefore
[8] and therefore
![]() (4.17)
(4.17)
From Equation (4.15) and Equation (4.17) one obtains
![]() (4.18)
(4.18)
Therefore
![]() (4.19)
(4.19)
Let ![]() be a circle wth the centre at point
be a circle wth the centre at point![]() . We assume now that
. We assume now that![]() . We will designate now
. We will designate now
![]() (4.20)
(4.20)
From Equation (4.6) and Equation (4.20) one obtains
![]() (4.21)
(4.21)
where ![]() Note that
Note that
![]() (4.22)
(4.22)
From (4.22) follows that for any ![]() there exists a prime number p such that
there exists a prime number p such that
![]() (4.23)
(4.23)
where ![]() From Equation (4.4)-Equation (4.6) follows
From Equation (4.4)-Equation (4.6) follows
![]() (4.24)
(4.24)
where ![]() Assume now that
Assume now that
![]() (4.25)
(4.25)
Having substituted RHS of the Equation (4.24) into Equation (4.25) one obtains
![]() (4.26)
(4.26)
From Equation (4.26) by using Equation (4.19) one obtains
![]() (4.27)
(4.27)
We choose now a prime ![]() such that
such that ![]() and
and ![]() Note that
Note that ![]() and therefore from Equation (4.19) and Equation (4.27) one obtains the contradiction. This contradiction com- pleted the proof.
and therefore from Equation (4.19) and Equation (4.27) one obtains the contradiction. This contradiction com- pleted the proof.
5. Generalized Lindemann-Weierstrass Theorem
Theorem 5.1. [4] Let ![]() be a polynomials with coefficients in
be a polynomials with coefficients in![]() . Assume that for any
. Assume that for any ![]() algebraic numbers over the field
algebraic numbers over the field ![]()
![]() form a complete set of the roots of
form a complete set of the roots of ![]() such that
such that
![]() (5.1)
(5.1)
and![]() . We assume now that
. We assume now that
![]() (5.2)
(5.2)
Then
![]() (5.3)
(5.3)
We will divide the proof into three parts.
Part I. The Robinson transfer
Let ![]() be a nonstandard polynomial such that
be a nonstandard polynomial such that
![]() (5.4)
(5.4)
Let![]() ,
, ![]() and
and ![]() be the quantities:
be the quantities:
![]() (5.5)
(5.5)
where in (5.5) we integrate in nonstandard complex plane ![]() along line
along line ![]() see Picture 1 .
see Picture 1 .
![]() (5.6)
(5.6)
where ![]() and where in (5.6) we integrate in nonstandard complex plane
and where in (5.6) we integrate in nonstandard complex plane ![]() along line with initial point
along line with initial point ![]() and which are parallel to real axis of the complex plane
and which are parallel to real axis of the complex plane![]() , see Picture 1 .
, see Picture 1 .
![]() (5.7)
(5.7)
where ![]() and where in (5.7) we integrate in nonstandard complex plane
and where in (5.7) we integrate in nonstandard complex plane ![]() along contour
along contour ![]() see Picture 1 .
see Picture 1 .
1. Using Robinson transfer principle [4] -[6] from Equation (5.5) and Equation (4.8) one obtains directly
![]() (5.8)
(5.8)
where ![]() We choose now infinite prime
We choose now infinite prime ![]() such that
such that
![]() (5.9)
(5.9)
2. Using Robinson transfer principle from Equation (5.6) and Equation (4.19) one obtains directly
![]() (5.10)
(5.10)
and therefore
![]() (5.11)
(5.11)
3. Using Robinson transfer principle from Equation (5.7) and Equation (4.21) one obtains directly
![]() (5.12)
(5.12)
where ![]() Note that
Note that ![]() there exists
there exists![]()
![]() (5.13)
(5.13)
4. From (5.13) follows that for any ![]() there exists an infinite prime
there exists an infinite prime ![]() such that
such that
![]() (5.14)
(5.14)
where ![]()
5. From Equation (5.5)-Equation (5.7) we obtain
![]() (5.15)
(5.15)
where ![]()
Part II. The Wattenberg imbedding ![]() into
into ![]()
1. By using Wattenberg imbedding ![]() and Gonshor transfer (see Subsection 2.8 Theorem 2.17) from Equation (5.8) one obtains
and Gonshor transfer (see Subsection 2.8 Theorem 2.17) from Equation (5.8) one obtains
![]() (5.16)
(5.16)
where ![]() We choose now an infinite prime
We choose now an infinite prime ![]() such that
such that
![]() (5.17)
(5.17)
2. By using Wattenberg imbedding ![]() and Gonshor transfer from Equation (5.10) one obtains directly
and Gonshor transfer from Equation (5.10) one obtains directly
![]() (5.18)
(5.18)
and therefore
![]() (5.19)
(5.19)
3. By using Wattenberg imbedding ![]() and Gonshor transfer from Equation (5.14) one obtains directly
and Gonshor transfer from Equation (5.14) one obtains directly
![]() (5.20)
(5.20)
4. By using Wattenberg imbedding ![]() and Gonshor transfer from Equation (5.15) one obtains directly
and Gonshor transfer from Equation (5.15) one obtains directly
![]() (5.21)
(5.21)
where ![]()
Part III. Main equality
Remark 5.1. Note that in this subsection we often write for a short ![]() instead
instead ![]() For example we write
For example we write
![]()
instead Equation (5.21).
Assumption 5.1. Let ![]() be a polynomials with coefficients in
be a polynomials with coefficients in![]() . Assume that for any
. Assume that for any ![]() algebraic numbers over the field
algebraic numbers over the field![]() :
: ![]()
![]()
![]() form a complete set of the roots of
form a complete set of the roots of ![]() such that
such that
![]() (5.22)
(5.22)
![]()
Note that from Assumption 5.1 follows that algebraic numbers over the field![]() :
: ![]()
![]() for any
for any ![]() form a complete set of the roots of
form a complete set of the roots of
![]() (5.23)
(5.23)
Assumption 5.2. We assume now that there exists a sequence
![]() (5.24)
(5.24)
and rational number
![]() (5.25)
(5.25)
such that
![]() (5.26)
(5.26)
and
![]() (5.27)
(5.27)
Assumption 5.3. We assume now for a short but without loss of generality that the all numbers ![]()
![]() are real.
are real.
In this subsection we obtain an reduction of the equality given by Equation (5.27) in ![]() to some equivalent equality given by Equation (3) in
to some equivalent equality given by Equation (3) in![]() . The main tool of such reduction that external countable sum defined in Subsection 2.8.
. The main tool of such reduction that external countable sum defined in Subsection 2.8.
Lemma 5.1. Let ![]() and
and ![]() be the sum correspondingly
be the sum correspondingly
![]() (5.28)
(5.28)
Then ![]()
Proof. Suppose there exists r such that ![]() Then from Equation (5.27) follows
Then from Equation (5.27) follows ![]() There- fore by Theorem 4.1 one obtains the contradiction.
There- fore by Theorem 4.1 one obtains the contradiction.
Remark 5.2. Note that from Equation (5.27) follows that in generel case there is a sequence ![]() such that
such that
![]() (5.29)
(5.29)
or there is a sequence ![]() such that
such that
![]() (5.30)
(5.30)
or both sequences ![]() and
and ![]() with a property that is specified above exist.
with a property that is specified above exist.
Remark 5.3. We assume now for short but without loss of generelity that (5.29) is satisfied. Then from (5.29) by using Definition 2.17 and Theorem 2.14 (see Subsection 2.8) one obtains the equality [4]
![]() (5.31)
(5.31)
Remark 5.4. Let ![]() and
and ![]() be the upper external sum defined by
be the upper external sum defined by
![]() (5.32)
(5.32)
Note that from Equation (5.31)-Equation (5.32) follows that
![]() (5.33)
(5.33)
Remark 5.5. Assume that ![]() and
and ![]() In this subsection we will write for a short
In this subsection we will write for a short ![]() iff
iff ![]() absorbs
absorbs![]() , i.e.
, i.e. ![]()
Lemma 5.2. ![]()
Proof. Suppose there exists ![]() such that
such that ![]() Then from Equation (5.33) one obtains
Then from Equation (5.33) one obtains
![]() (5.34)
(5.34)
From Equation (5.34) by Theorem 2.11 follows that ![]() and therefore by Lemma 5.1 one obtains the contradiction.
and therefore by Lemma 5.1 one obtains the contradiction.
Theorem 5.2. [4] The equality (5.31) is inconsistent.
Proof. Let us considered hypernatural number ![]() defined by countable sequence
defined by countable sequence
![]() (5.35)
(5.35)
From Equation (5.31) and Equation (5.35) one obtains
![]() (5.36)
(5.36)
where
![]() (5.37)
(5.37)
Remark 5.6. Note that from inequality (5.12) by Gonshor transfer one obtains
![]() (5.38)
(5.38)
Substitution Equation (5.21) into Equation (5.36) gives
![]() (5.39)
(5.39)
Multiplying Equation (5.39) by Wattenberg hyperinteger ![]() by Theorem 2.13 (see sub- section 2.8) we obtain
by Theorem 2.13 (see sub- section 2.8) we obtain
![]() (5.40)
(5.40)
By using inequality (5.38) for a given ![]()
![]() we will choose infinite prime integer
we will choose infinite prime integer ![]() such that:
such that:
![]() (5.41)
(5.41)
Therefore from Equations (5.40) and (5.41) by using definition (2.15) of the function ![]() given by Equation (2.20)-Equation (2.21) and corresponding basic property I (see Subsection 2.7) of the function
given by Equation (2.20)-Equation (2.21) and corresponding basic property I (see Subsection 2.7) of the function ![]() we obtain
we obtain
![]() (5.42)
(5.42)
From Equation (5.42) finally we obtain the main equality
![]() (5.43)
(5.43)
We will choose now infinite prime integer ![]() in Equation (3.56)
in Equation (3.56) ![]() such that
such that
![]() (5.44)
(5.44)
Hence from Equation (5.16) follows
![]() (5.45)
(5.45)
Note that ![]() Using (5.44) and (5.45) one obtains:
Using (5.44) and (5.45) one obtains:
![]() (5.46)
(5.46)
Using Equation (5.11) one obtains
![]() (5.47)
(5.47)
Part IV. The proof of the inconsistency of the main equality (5.43)
In this subsection we wil prove that main equality (5.43) is inconsistent. This proof is based on the Theorem 2.10 (v), see Subsection 2.6.
Lemma 5.3. The equality (5.43) under conditions (5.46)-(5.47) is inconsistent.
Proof. (I) Let us rewrite Equation (5.43) in the short form
![]() (5.48)
(5.48)
where
![]() (5.49)
(5.49)
From (5.46)-(5.47) follows that
![]() (5.50)
(5.50)
Remark 5.7. Note that ![]() Otherwise we obtain that
Otherwise we obtain that
![]() (5.51)
(5.51)
But the other hand from Equation (5.48) follows that
![]() (5.52)
(5.52)
But this is a contradiction. This contradiction completed the proof of the statement (I).
(II) Let ![]() and
and ![]() be the external sum correspondingly
be the external sum correspondingly
![]() (5.53)
(5.53)
Note that from Equation (5.43) and Equation (5.53) follows that
![]() (5.54)
(5.54)
Lemma 5.4. Under conditions (5.46)-(5.47)
![]() (5.55)
(5.55)
and
![]() (5.56)
(5.56)
Proof. First note that under conditions (5.46)-(5.47) one obtains
![]() (5.57)
(5.57)
Suppose that there exists ![]() such that
such that ![]() hen from Equation (5.54) one obtains
hen from Equation (5.54) one obtains
![]() (5.58)
(5.58)
From Equation (5.58) by Theorem 2.17 one obtains
![]() (5.59)
(5.59)
Thus
![]() (5.60)
(5.60)
From Equation (5.60) by Theorem 2.11 follows that ![]() and therefore by Lemma 5.2 one obtains the contradiction. This contradiction finalized the proof of the Lemma 5.4.
and therefore by Lemma 5.2 one obtains the contradiction. This contradiction finalized the proof of the Lemma 5.4.
(III)
Remark 5.8. (i) Note that from Equation (5.49) by Theorem 2.10 (v) follws that ![]() has the form
has the form
![]() (5.61)
(5.61)
where
![]() (5.62)
(5.62)
(ii) Substitution by Equation (5.61) into Equation (5.48) gives
![]() (5.63)
(5.63)
Remark 5.9. Note that from (5.63) by definitions follows that
![]() (5.64)
(5.64)
Remark 5.10. Note that from (5.62) by construction of the Wattenberg integer ![]() obviously follows that there exists some
obviously follows that there exists some ![]() such that
such that
![]() (5.65)
(5.65)
Therefore
![]() (5.66)
(5.66)
Note that under conditions (5.46)-(5.47) and (5.66) obviously one obtains
![]() (5.67)
(5.67)
From Equation (5.63) follows that
![]() (5.68)
(5.68)
Therefore
![]() (5.69)
(5.69)
From (5.69) follows that
![]() (5.70)
(5.70)
Note that from (5.70) by Theorem 2.8 (see Subsection 2.5) and Formula (5.32) one otains
![]() (5.71)
(5.71)
From Equation (5.70)-Equation (5.71) follows that
![]() (5.72)
(5.72)
Thus
![]() (5.73)
(5.73)
and therefore
![]() (5.74)
(5.74)
But this is a contradiction. This contradiction completed the proof of the Lemma 5.3.
Remark 5.11. Note that by Definition 2.18 and Theorem 2.18 from Assumption 5.1 and Assumption 5.2 follows
![]()
Theorem 5.3.The equality (5.75) is inconsistent.
Proof. The proof of the Theorem 5.3 obviously copies in main details the proof of the Theorem 5.3.
Theorem 5.3 completed the proof of the main Theorem 1.6.