Extension of Generalized Bernoulli Learning Models

B. S. El-Desouky, F. A. Shiha, A. M. Magar

Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt.

DOI: 10.4236/ojmsi.2015.31003                

Abstract

In this article, we study the generalized Bernoulli learning model based on the probability of success p_i = a_i /n where i = 1,2,...n 0<a₁<a₂<...<a_n<n and n is positive integer. This gives the previous results given by Abdulnasser and Khidr [1], Rashad [2] and EL-Desouky and Mahfouz [3] as special cases, where p_i = i/n p_i = i²/n² and p_i = i^p/n^p respectively. The probability function P(W_n = k) of this model is derived, some properties of the model are obtained and the limiting distribution of the model is given.

Keywords

Stirling Numbers, Bernoulli Learning Models, Comtet Numbers, Inclusion-Exclusion Principle

1. Introduction

In industry, training programmes are conducted with the aim of training new workers to do particular job repeatedly every day. It is assumed that a particular trainee will show progress proportional to the number of days he attends the program, otherwise his ability will be different from one day to another, see [1] [4] .

Let 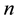be the length of a programme in days and the number of repetitions of the job per day a trainee has to do. If a trainee is responding to the instructions, it would be reasonable to assume the probability that he will do a single job right, i.e. the probability of success on the 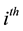day is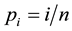, see Abdulnasser and Khidr [1] ,

and hence the probability that he will do 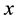jobs correctly out of jobs on the day is 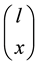, and.

When a trainee is not responding to the instructions, will be a constant, To test whether a trainee is responding or not, we test if is varying or sustaining a constant value This can be done by computing the total number of jobs that have been done correctly over the whole period of the program.

Let stand for the number of jobs done correctly out of jobs on day, and ,. In case, , the distribution of will be.

In this article, we study a generalization of Bernoulli learning model based on probability of success where positive integer, are real numbers, and and is positive integer. This gives the previous results given in [1] - [3] as special cases, where and respectively. In Section 2, the probability function of this model and some properties of the model are obtained. In Section 3, we derive the limiting distribution of the model. Finally, in Section 4, we discuss some special cases.

2. The Generalized Bernoulli Learning Model

Theorem 1. The distribution function of is

(1)

where .

Proof. To derive the distribution of Bernoulli learning model based on the sum of the independent random variable ,

where the probability of success is we define the event as the event, see [5] , and the sum

where the generalized Stirling number of the first kind (Comtet numbers), defined by Comtet in [6] [7] as follows

where, for more details, see [8] and [9] .

Employing the inclusion-exclusion principle, see [5] , we get

then

hence

this yields (1).

Lemma 1.

(2)

(3)

Proof. Consider the pair of inverse relation, see [10]

(4)

Then using (1), let

Hence from (4), we get

(5)

and setting, we have

(6)

But we have, see [7]

(7)

Thus and this yields (2).

If putting in (5), we get

using (7), we have, then

hence

this yields (3).

3. Limiting Distribution of the Bernoulli Learning Model

In this section we study the limiting distribution of the Bernoulli learning model based on the probability with success

Theorem 2. Let where and are independent random variables. Then where i.e. is as

Proof. The moment generating function of is

and the moment generating function of is

therefore, we have

by using (2) and (3), we obtain

(8)

which is the moment generating function of standard normal distribution

4. Some Special Cases

In this section we discuss some special cases as follows.

i) Setting the probability of successes we have the results derived in [1] , as special case

Theorem 3. The distribution of is given by [1]

(9)

where are the usual stirling numbers of the first kind, see [10] .

Also, they obtained the limiting distribution of learning model, mean and variance as follows.

Theorem 4. Let where and’s are independent random variables. Then where i.e. has as

Lemma 2.

(10)

ii) Setting the probability of successes we have the results derived in [2] , as special case

Theorem 5. The distribution of is given by [2]

(11)

Lemma 3.

iii) Setting the probability of successes we have the results derived in [3] , as special case

Theorem 6.

(12)

where, and p-Stirling numbers, see [11] [12] .

Theorem 7. Let where and are independent random variables. Then where i.e. has as

Lemma 4.

5. Conclusion

Our main goal of this work is concerned with studying the extension of generalized Bernoulli learning model with probability of success and is positive integer. Some previous results, see [1] - [3] , are concluded as special cases of our result, that is for and respectively. The mean and variance of the model are obtained. Finally, the limiting distri- bution of the general model is derived. This model has many applications in industry, specially for training pro- grammes.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Abdulnasser, T. and Khidr, A.M. (1981) On the Distribution of a Sum of Non-Identical Independent Binomials. Journal of University of Kuwait, 8, 109-115.
[2]	Rashad, A.M. (1998) On the Sum of Non-Identical Random Variables. M.Sc. Thesis, Faculty of Science, Aswan.
[3]	EL-Desouky, B.S. and Mahfouz, K.M. (2012) A Generalization of Bernolli Learning Models. Kuwait Journal of Science and Engineering, 39, 31-44.
[4]	Janardan, K.G. (1997) Bernoulli Learing Models: Uppulur numbers. In: Balakrishnan, N., Ed., Advances in Combinatorial Methods and Applications to Probability and Statistics, Birkhäuser. Statistics for Industry and Technology, Boston, 471-480. http://dx.doi.org/10.1007/978-1-4612-4140-9_29
[5]	Parzen, E. (1960) Modern Probability Theory and Its Applications. John Wiley & Sons, Hoboken.
[6]	Comtet, M.L. (1972) Nombers de Stirling generoux et functions symetriques. C. R. Acad. Sci. Paris, Ser. A, 275, 747-750.
[7]	Comtet, M.L. (1974) Advanced Combinatorics. Reidel, Dordrecht-Holland. http://dx.doi.org/10.1007/978-94-010-2196-8
[8]	EL-Desouky, B.S. and Cakic, N.P. (2011) Generalized Higher Order Stirling Numbers. Mathematical and Computer Modelling, 54, 2848-2857. http://dx.doi.org/10.1016/j.mcm.2011.07.005
[9]	EL-Desouky, B.S., Cakic, N.P. and Mansour, T. (2010) Modified Approach to Generalized Stirling Numbers via Differential Operators. Applied Mathematics Letters, 23, 115-120. http://dx.doi.org/10.1016/j.aml.2009.08.018
[10]	Riordan, J. (1968) Combinatorial Identities. John Wiley & Sons, New York. London, and Sydney.
[11]	Beardon, A.F. (1996) Sums of Powers of Integers. The American Mathematical Monthly, 103, 201-213. http://dx.doi.org/10.1016/j.aml.2009.08.018
[12]	Sun, Y. (2006) Two Classes of p-Stirling Numbers. Discrete Mathematics, 306, 2801-2805. http://dx.doi.org/10.1016/j.disc.2006.05.016