1. Introduction
Disturbances propagation in the boundary layers is associated with the processes of convection and diffusion [1] . Analysis of three-dimensional boundary layer equations [2] showed that the characteristics of this system of equations are lines normal to the streamlined surface. The appearance of these characteristics corresponds to the disturbances propagation with infinite velocity normal to the surface. These effects are associated with the pro- cesses of diffusion, which in reduced boundary layer equations take place in one direction. To describe the pro- cesses of disturbances propagation associated with convection, we should analyze the characteristics of the boundary layer equations without oldest derivatives (subcharacteristics). The equations of 2D unsteady boundary layer also allow the analysis of the characteristics and subcharacteristics [2] . However, because of the no slip condition on the surface, the flow near wall is subsonic, so there is a physical possibility for disturbances spread upstream. The results of experimental investigation of an upstream disturbances propagation are presented in [3] . Mathematical model describing disturbances propagation, implies that the pressure distribution is determined by viscous-inviscid interaction processes. At the same time, the classical theory of the boundary layer does not allow to describe such processes as the pressure distribution is prescribed. Effects of strong local viscous-inviscid interaction allow as well describing local separated flows [4] [5] , and flows with large local gradients [6] [7] .
Analysis of disturbances propagation in three-dimensional boundary layers for strong interaction led to determination of appropriate subcharacteristic surfaces [8] , separating the field of subcritical flow (subsonic in average) and supercritical flow (supersonic in average) in hypersonic boundary layer near the delta wing. Below unsteady flows in laminar boundary layers are investigated for the regime of strong viscous-inviscid interaction with the special emphasis on Prandtl number and specific heat ratio influence. Such results have not been obtained before.
2. Problem Formulation
It is supposed that flat plate is placed in hypersonic flow at zero angle of attack. It is supposed as well that strong viscous-inviscid interaction regime is realyzed [9] , for which next limits are valid:
 (1)
(1)
where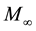 : Mach number of external glow,
: Mach number of external glow, 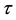 is the nondimensional boundary layer thickness
is the nondimensional boundary layer thickness
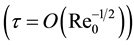 . For Cartesian coordinates directed along the surface and normally to the plate surface, time,
. For Cartesian coordinates directed along the surface and normally to the plate surface, time,
velocity vector components, density, pressure, full enthalpy, dynamic viscosity coefficient next definitions are intorduced: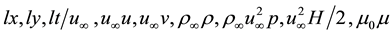 , correspondingly. Parameter
, correspondingly. Parameter 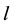 is a characteristic plate length. Index
is a characteristic plate length. Index  corresponds to the dimensional external undisturbed flow values, index 0 corresponds to the dimensional value of dynamic viscosity coefficient at stagnation temperature. It is supposed that Reynolds number
corresponds to the dimensional external undisturbed flow values, index 0 corresponds to the dimensional value of dynamic viscosity coefficient at stagnation temperature. It is supposed that Reynolds number 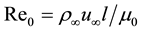 is large but doesn’t exceed critical value corresponding to the laminar-turbulent transition. It was shown that for large Mach numbers critical Reynolds number is large [10] .
is large but doesn’t exceed critical value corresponding to the laminar-turbulent transition. It was shown that for large Mach numbers critical Reynolds number is large [10] .
Corresponding to the strong viscous-inviscid interaction theory disturbed flow region near the plate contains two-subregions: 1―inviscid flow between shock wave and boundary layer exteral edge, 2―viscous flow in the boundary layer.
In the subregion 1 next asymptotic expansions are valid:
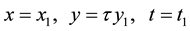 (2)
(2)
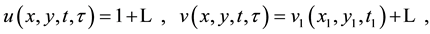

Substitution of (2) expansions into the Navier-Stokes equations and limiting procedure (1) leads to the next system of equations
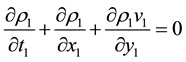
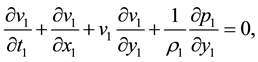
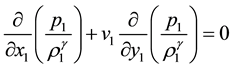
With the next boundary conditions on the shock wave:
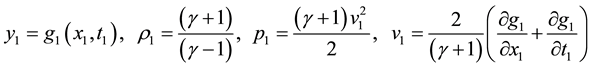
And on external edge of the boundary layer
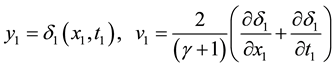
For subsequent analysis it is needed to get expression connecting boundary layer thickness ![]() or vertical velocity
or vertical velocity ![]() and induced pressure
and induced pressure![]() . Approximate formula is used
. Approximate formula is used
![]() (3)
(3)
which is the tangent wedge formula generalization for unsteady regime.
For subregion 2 next expansions are valid:
![]() (4)
(4)
![]()
![]()
![]()
Substitution (4) into the Navier-Stokes equations and limiting procedure (1) give unsteady boundary layer equations. Next transformation
![]()
![]()
leads corresponding mathematical problem to the next form
![]() (5)
(5)
![]()
![]() ,
,
![]()
![]()
where is supposed that dynamic viscosity coefficient linearly depends on the temperature.
The last boundary condition corresponds to the prescribed base pressure value.
3. Subcharacteristics Determination
Let us determine characteristic (subcharacteristic) surfaces![]() , associated with the induced pressure
, associated with the induced pressure![]() , which is not prescribed and should be determined as a result of solution.
, which is not prescribed and should be determined as a result of solution.
After transformation
![]() (6)
(6)
Boundary problem (5) takes the form
![]() (7)
(7)
where
![]()
![]()
Interaction condition connecting pressure distribution and boundary layer thickness may be transformed to get next relation
![]() (8)
(8)
Derivative in the left part of (8) may be expressed in accordance with the boundary layer thickness
![]()
The problem formulation (5) may be used to determine derivatives on the ![]() variable
variable
![]()
After some transformations using (7)-(8) relations, the next expression may be obtained
![]() (9)
(9)
where
![]()
Relation determining subcharacteristic surface has then the form
![]() (10)
(10)
where a is an average speed of sound or velocity of subcharacteristic surface
![]()
Expression (10) is in fact known integral Pearson generalization [11] .
![]() (11)
(11)
The sign of ![]() depends on average Mach number value in the boundary layer. Supersonic (in average ) flow is characterized by the negative L value, at the same time positive L value corresponds to the subsonic (in average) flow.
depends on average Mach number value in the boundary layer. Supersonic (in average ) flow is characterized by the negative L value, at the same time positive L value corresponds to the subsonic (in average) flow.
Relation (10) has simple physical explanation. In hypersonic boundary layer exists average velocity value. If average speed of sound is larger than this average velocity than the flow inside boundary layer is subcritical and disturbances can propagate upstream, otherwise the flow will be supercritical.
Relataion (10) may be deduced from (11) by easy way. If we will use moving coordinate ![]() system instead of steady system
system instead of steady system ![]()
![]()
In the moving coordinate system velocity in the boundary layer equals![]() , while difference
, while difference ![]()
![]() is proportional to the temperature and doesn’t change. Introducing expressions for
is proportional to the temperature and doesn’t change. Introducing expressions for ![]() и
и![]() to the (11) we can arrive at (10) expression.
to the (11) we can arrive at (10) expression.
4. Solution Examples
As an example we can get dependence of an upstream disturbances propagation on specific heat ratio and on
![]()
Figure 1. Upstream disturbances propagation velocity a as a specific heat ratio ![]() and Prandtl number Pr function.
and Prandtl number Pr function.
Prandtl number for self similar boundary layer equations solution.
Velocity and full enthalpy profiles were obtained as a result of the next boundary problem solution
![]()
![]() (12)
(12)
![]()
![]()
These profiles have been used to obtain upstream disturbances propagation velocity![]() .
.
Dependences of an upstream disturbances propagation velocity ![]() on specific heat ratio
on specific heat ratio ![]() are presented on the Figure 1. Three curves correspond to different values of the Prandtl number. One curve corresponds to small Prandtl number value
are presented on the Figure 1. Three curves correspond to different values of the Prandtl number. One curve corresponds to small Prandtl number value![]() . Second curve corresponds to the
. Second curve corresponds to the ![]() and the third one corresponds to large Prandtl value
and the third one corresponds to large Prandtl value![]() .
.
We may conclude that Prandtl number influence on ![]() parameter is small. In fact Prandtl number influences on average velocity and full enthalpy profiles in the boundary layer.
parameter is small. In fact Prandtl number influences on average velocity and full enthalpy profiles in the boundary layer.
It was supposed that specific heat ratio changes from unity (for polyatomic gas) up to the value 5/3 (for monoatomic gas). It may be concluded that speed of upstream disturbances propagation is larger for larger ![]() values. It may be shown that parameter
values. It may be shown that parameter ![]() tends to zero if specific heat ratio
tends to zero if specific heat ratio ![]() tends to unity.
tends to unity.
Acknowledgements
This work was partially supported by the Russian Foundation for Basic Research (project № 13-01-06249).