The Stability of Highly Pathogenic Avian Influenza Epidemic Model with Saturated Contact Rate ()
1. Introduction
Avian influenza virus belongs to the influenza A virus. According to the difference of the pathogenic Avian influenza virus in chicken and turkey, we divided it into three levels: high, medium, low/non pathogenic. Because of the bird flu virus hemagglutinin structure characteristics, general infected birds, when the virus genetic reassortment during replication, causing structural changes. The Avian influenza virus which acquires the ability to infect people, can make adult infect the Avian influenza disease. The highly pathogenic Avian influenza has a high death rate, which is about 100 percent for birds and more than 70 percent for humans [1] .
Up to now, we found that Avian influenza virus subtypes which can directly infect human are: H5N1, H7N1, H7N2, H7N3, H7N7, H9N2, H7N9, subtype. Among them, the new subtype Avian influenza virus H7N9 subtype, which was first discovered in 2013 March, and the high pathogenic Avian influenza H5N1 subtype, are particularly noteworthy. The Avian influenza virus not only caused human casualties, but also hit the poultry industry.
Avian influenza virus (H5N1 subtype Avian influenza virus) had 12 human infections in Hongkong, including 6 deaths. According to the WHO’s statistics, 393 people around the world in more than 15 countries and regions were infected, including 248 deaths; the mortality rate was 0.63. Since 2003, 31 people have been infected with Avian influenza in China, including 21 deaths. Although people infection probability is not high, the mortality rate is very high. By March 2013, the world has reported a total of human infection of highly pathogenic H5N1 Avian influenza in 622 cases, including 371 deaths. The distribution of cases in 15 countries, including China, is found in 45 cases, 30 cases of death. Most of human infections with H5N1 Avian influenza are young people and children. In March 2013, human infection with H7N9 Avian influenza was first found in China. By May 1, 2013, Shanghai, Anhui, Jiangsu, Zhejiang, Beijing, Henan, Shandong, Jiangxi, Hunan, Fujian and other 10 provinces (city) have reported 127 confirmed cases, including 26 death cases. The cases in the majority are with the elderly, men more than women [2] .
The present study found that people are infected with bird flu infection for the virus’s birds, but the transmission is still to be defined. Research suggests that the main way of human infection with the H5N1 Avian influenza is in close contact with poultry, high-risk behavior, including the slaughter, feathers and processing of infected poultry. In a few cases, when children frequently play in the backyard poultry regional, the exposure poultry manure was also thought to be a source of infection. At present, most of the researched evidences indicate the presence of bird-human transmission; there may be an environment-human (birds excrement pollution) transmission, and a few non sustained human-human transmission of H5N1. Now H7N9 Avian influenza patients are infected through direct contact with poultry or the items, environment which are contaminated by feces. Human infection with H7N9 Avian influenza is still sporadic, although there have been cases of aggregation of individual families; but it is not currently found that the virus has sustained human-human transmission capacity.
At present, some authors have researched some Avian influenza model [3] [4] , they had constructed a mathe- matical model which interprets the spread of Avian influenza from the bird world to the human world. Literature [5] has introduced a piecewise treatment function. When the number of the infective had not exceeded the maxi- mum treatment capacity, the treatment rate was proportional to the number of the infective. When the number of the infective had exceeded the maximum treatment capacity, it took maximum saturation treatment value. Lit- erature [6] -[8] have studied of SIR model with saturated treatment rate. In the literature [8] , the saturated
treatment rate is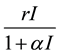 , where r is the cure rate and
, where r is the cure rate and  is the parameters of infection which is due to delayed
is the parameters of infection which is due to delayed
treatment. The conclusion had indicated that in the prevention and treatment of Avian flu drugs under the condition of limited, culling of infected poultry was the most effective way to control the spread of Avian flu in humans. Literature [9] [10] have proposed the model of highly pathogenic Avian influenza.
In this paper, the authors propose a Avian influenza model with saturated contact rate [11] ,
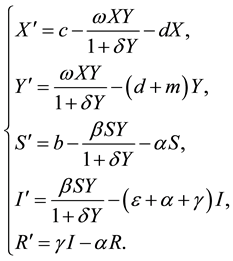 (1.1)
(1.1)
In system (1.1), the human is divided into three compartments: Susceptible (S), infected (I), recovery (R). The birds are divided into susceptible poultry (X) and infected poultry (Y). The parameters c and b are respectively the natural birth rate of Avian and human. d and  are respectively the natural mortality of poultry and human. m and
are respectively the natural mortality of poultry and human. m and  are respectively the poultry and human mortality due to illness.
are respectively the poultry and human mortality due to illness. 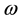 stands for infectious rate of susceptible poultry to infected poultry.
stands for infectious rate of susceptible poultry to infected poultry. 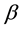 stands for infected poultry of the infection rate of susceptible individuals.
stands for infected poultry of the infection rate of susceptible individuals. 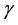 is the recovery rate that infects individuals through treatment. When Y is small, the contact ratio, infected poultry and susceptible poultry, is approximatively proportional to the Y; With the increase of Y, the con-
is the recovery rate that infects individuals through treatment. When Y is small, the contact ratio, infected poultry and susceptible poultry, is approximatively proportional to the Y; With the increase of Y, the con-
tact rate gradually reaches saturation. When Y is very large, it is close to a constant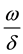 . The same way to ex-
. The same way to ex-
plain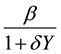 , that is to say,
, that is to say, 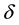 is a parameter, which is effects of infectious diseases, when the contact rate of
is a parameter, which is effects of infectious diseases, when the contact rate of
the disease is saturated. The transmission process of the disease is shown in Figure 1.
2. The Existence of the Equilibrium Point
The first four equations of system (1.1) do not contain R, by the method of van den Driessche and Watmough Diekmann [12] , we only need to study the following system:
 (2.1)
(2.1)
It’s easy to get a disease-free equilibrium of the system (2.1)  is
is , by the method of van den Driessche and Watmough, we can get the basic reproductive number of the system (2.1)
, by the method of van den Driessche and Watmough, we can get the basic reproductive number of the system (2.1)

By the positive of the endemic equilibrium point, we can get that if R0 > 1, there is a unique endemic equilibrium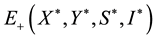 , which satisfied:
, which satisfied:
![]()
![]()
So, we can get the following theorem:
Theorem 2.1 If R0 ≤ 1, the system (2.1) only exists the disease-free equilibrium![]() ; when R0 > 1, there exists only one endemic equilibrium
; when R0 > 1, there exists only one endemic equilibrium
![]() .
.
3. The Stability of the Disease-Free Equilibrium
The Jacobian matrix of system (2.1) is
![]() ,
,
which in the disease-free equilibrium E0, is
![]()
The characteristic equation of the Jacobian matrix ![]() is
is
![]()
Here, ![]() , λ denotes the indeterminate of the polynomial. If and only if R0 ≤
, λ denotes the indeterminate of the polynomial. If and only if R0 ≤
1, all roots of this characteristic equation have negative real parts. It implies that E0 is locally asymptotically stable. Then we can get the following theorem:
Theorem 3.1 If R0 ≤ 1, the disease-free equilibrium E0 is locally asymptotically stable; if R0 > 1, the disease- free equilibrium E0 is unstable.
Next, we discuss the global stability of E0, considering the Liapunov function [13] ![]() , then
, then
![]()
when![]() , we can get
, we can get![]() , and
, and ![]() has no other closed trajectory in addition to E0. Then we can get the following theorem:
has no other closed trajectory in addition to E0. Then we can get the following theorem:
Theorem 3.2 If![]() , the disease-free equilibrium E0 is globally asymptotically stable.
, the disease-free equilibrium E0 is globally asymptotically stable.
4. The Stability of the Endemic Equilibrium
The Jacobian matrix of system (2.1), which in the endemic equilibrium E+, is
![]()
where
![]()
![]()
![]()
Thus, ![]() evaluated is stable if and only if so are A and C. Then the characteristic equation of the matrix A is
evaluated is stable if and only if so are A and C. Then the characteristic equation of the matrix A is
![]()
where,
![]()
Obviously, when R0 > 1, h1 > 0, h2 > 0. By the Harwize criterion, it implies that the characteristic roots of matrix A have negative real parts. then, we analyze the characteristics equation of the matrix C
![]()
Easily, if and only if R0 > 1, all roots of this characteristic equation have negative real parts. So, we can get the following theorem:
Theorem 4.1 If R0 > 1, the endemic equilibrium E+ is locally asymptotically stable.
Next, we discuss the global stability of E+, considering the Liapunov function
![]() , then derivated W2 about system (2.1),
, then derivated W2 about system (2.1),
![]()
By the relationship of arithmetic mean and geometric mean, we can know![]() . That is to say,
. That is to say,
![]() . If and only if
. If and only if![]() ,
,![]() . Thus, by LaSalle Invariance Principle [14] , we can get the following theorem:
. Thus, by LaSalle Invariance Principle [14] , we can get the following theorem:
Theorem 4.2 If R0 > 1, the endemic equilibrium E+ is globally asymptotically stable.
5. The Numerical Simulations
In this section, the model has been analyzed numerically by using MAT-LAB 7.5.0, to confirm the results we have obtained. For this purpose we have used the following set of parameter values:
When c = 2; β = 0.01; d = 0.03; ω = 0.014; m = 0.97; b = 1; α = 0.069; ε = 0.63; γ = 0.301; δ = 0.05, then R0 = 0.9333. These parameters values satisfy the condition R0 < 1. Thus, the two images of Figure 2 show that if R0 < 1, the disease-free equilibrium E0 is global asymptotically stable.
When c = 2; β = 0.01; d = 0.03; ω = 0.02; m = 0.97; b = 1; α = 0.069; ε = 0.63; γ = 0.301; δ = 0.05 then R0 = 1.3333; These parameters values satisfy the condition R0 > 1. Thus, the two image of Figure 3 shows that if R0 > 1, the unique endemic equilibrium E* is global asymptotically stable.
6. Conclusion
In this paper we have discussed the stability of highly pathogenic Avian influenza epidemic model with saturated contact rate. We get the reproduction number R0; it is the threshold which is endemic or not. If R0 ≤ 1,
![]()
![]() (a) (b)
(a) (b)
Figure 2. c = 2; β = 0.01; d = 0:03; ω = 0.014; m = 0.97; b = 1; α = 0.069; ε = 0.63; γ = 0.301; δ = 0.05; R0 = 0.9333.
![]()
![]() (a) (b)
(a) (b)
Figure 3. c = 2; β = 0.01; d = 0.03; ω = 0.02; m = 0.97; b = 1; α = 0.069; ε = 0.63; γ = 0.301; δ = 0.05; R0 = 1.3333.
the disease-free equilibrium is global asymptotic stability which implies that the disease will be extinct. If R0 > 1, the endemic equilibrium E+ is globally asymptotically stable, that implies that the disease will sustain and lead to epidemic disease eventually. In order to prevent epidemics, through the analysis of the model, we can get: reducing the activities of the poultry market; culling or burying the infected poultry. That the infected poultry feces get disinfected or burned can prevent the pollution of the surrounding water. The government must strictly manage cooked poultry meat, and meat sources. Traditional farming poultry from backyard changes the concentration of scale breeding, slaughter processing and scientific transport, raising poultry breeding, circulation biological safety level, thereby reduces the population of live poultry or poultry exposure opportunity. Early discovery, early diagnosis of Avian influenza are the implementation of case isolation and diagnosis and treatment timely, effectively and reasonably.
NOTES
*Corresponding author.