A Geometric Approach to the Design of Serial and Parallel Manipulators with Passive Joints ()
1. Introduction
Serial and parallel robots are widely used in remote and harsh environments where humans cannot or do not want to operate. The need for a rigorous theory on what happens when joint failure occurs is thus important to be able to cope with unforeseen events such as actuation failure. This paper endeavors to convey a complete theory of the effects that passive joints have on serial and parallel manipulators when external forces are present. We start by looking at how joint failure affects the mobility of closed chain manipulators. We are interested in the undesired motion generated by the passive joints that cannot be compensated for by the active joints. For parallel manipulators, joint failure may or may not allow a motion generated by the passive joints. If the mani- pulator does not allow such a passive motion, we will denote it equilibrated. In this case it can resist a wrench in an arbitrary direction either through kinematic constraints or through actuator torques. We obtain this if the manipulator, considering the passive joints only, has mobility equal to zero, i.e. we do not want the passive joints to allow any motion when the active joints are locked. If this property is satisfied the manipulator does not have an unstable singularity, following the classification in Matone and Roth [1] . On the other hand, for serial manipulators joint failure will always result in an undesired motion if an arbitrary external force is present. In this case we investigate under what conditions, i.e. for what external forces and for what configurations, the external forces do not affect the motion of the passive joints. We will say that the manipulator is conditionally equilibrated with respect to an external force at all configurations for which the passive joints are not affected by the given force.
Many papers discussing the mobility of parallel manipulators and the relation between the active and passive joints can be found in literature. The Jacobian of the parallel manipulator is investigated in Liu et al. [2] and Bicchi and Prattichizzo [3] where the passive joint accelerations are found from the active joint accelerations by dividing the Jacobian into an active and a passive part. For non-overconstrained mechanisms, i.e. when there are no redundant constraints, we can find the mobility by the well known Grübler formula [4] . For overconstrained mechanisms there are many approaches to determine the mobility. In Dai et al. [5] the mobility of the mecha- nism is found from the constraint space. The constraints of the system are found systematically and the redun- dant constraints are identified. The mobility is then found by adding the degrees of freedom represented by these redundant constraints to the Grübler formula for non-overconstrained mechanisms. This approach illustrates well the effect of redundant constraints in the mechanism.
The mobility can also be found by the motion space as in Rico et al. [6] [7] . The degree of freedom of the motion of the end effector is first found. Then the degree of freedom of the self-motion manifold of each chain is added. By this approach the redundant constraints are not found directly, but this approach gives valuable in- sight into where to place redundant actuators in the mechanism.
Even though the mobility of closed chain manipulators is given a lot of attention in literature, there does not seem to be a thorough treatment of mobility in the light of joint failure. In this paper we are mainly concerned with the effects of torque failure [1] , also known as free-swinging joint faults (FSJF), see English and Macie- jewski [8] and Tinós et al. [9] [10] . This occurs when an active joint suddenly loses its actuation and starts behaving like a passive joint. For a comprehensive treatment on how to identify joint failures see Tinós et al. [10] . Once these are identified the appropriate control actions should be applied to minimise damage to the surroundings.
Passive joints will in general not be an intrinsic property of an open chain manipulator as this would make the manipulator collapse due to gravity or other external forces. In the case of free-swinging joint faults, however, the study of passive joints is important also for serial manipulators in order to prevent damage from the free- swinging joint. FSJF may occur for any joint and for any configuration of the manipulator. A systematic and rigorous description is thus essential in order to find a good and fast solution and to prevent damage to the surroundings. For serial manipulators the strongest property we can obtain is that the robot is conditionally equilibrated, i.e. a set of configurations for which the manipulator is equilibrated with respect to a given external force. Passive joints in serial manipulators are treated only briefly in literature, see for example Oriolo and Nakamura [11] and Arai and Tachi [12] , and case studies such as the Acrobot [13] .
Parallel manipulators can be designed such that all the degrees of freedom of the motion remain controllable when joint failure occurs for an arbitrary joint. This will, however, require more active joints than necessary to control the degrees of freedom of the manipulator. This actuator redundancy is in many cases undesirable due to manufacturing and maintenance costs, weight, performance, and so on. If the fault tolerance problem is not addressed in the design process it must be handled in the control of the manipulator in the case of such an occurrence. In this case the serial and parallel manipulators are treated in a similar manner and we search the configuration space of the manipulator for a set of joint positions for which the manipulator remains equilibrated for a given external force.
The approach presented in this paper is in itself very simple. First, we use Grübler’s formula or a generic method based on the results in Rico et al. [6] [7] to verify whether the manipulator, considering the passive joints only, generates a non-trivial motion. This is based on the results found in From and Gravdahl [14] . Then, if the passive joints of the manipulator allow a motion, we investigate what kind of motion it implements. From this we can conclude the two main results of this paper: 1) given a mechanism, with respect to what kind of external forces is the manipulator equilibrated; and 2) given an external force, what kind of mechanism and for what configurations is the mechanism equilibrated with respect to the external force.
In Meng et al. [15] , a precise geometric theory for analysis and synthesis of sub-6 DOF manipulators was presented. The low dimensional subgroups or submanifolds of 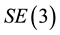 were used to represent the lower pairs, or primitive generators, while the high dimensional subgroups were used to represent the desired end-effector motion types. Given a desired end-effector motion type as a Lie subgroup or a submanifold, the synthesis problem was solved for serial and parallel manipulators. Then, from a pre-specified list of primitive generators, all possible serial and parallel arrangements of the primitive generators so that the resulting manipulator has the desired end-effector motion type were found. Using the formalism of [15] , we find that a mechanism is con- ditionally equilibrated with respect to an external force if the mechanism considering the passive joints only, is a motion generator of a motion for which the reciprocal product with the external force vanishes. Thus, while [15] uses the general concept of motion type (reference frame not specified) in their definition of motion generator, we will use a motion defined in a specific coordinate frame in our definitions. This allows us to verify resistance with respect to a specific external force, as opposed to a type or class of forces.
were used to represent the lower pairs, or primitive generators, while the high dimensional subgroups were used to represent the desired end-effector motion types. Given a desired end-effector motion type as a Lie subgroup or a submanifold, the synthesis problem was solved for serial and parallel manipulators. Then, from a pre-specified list of primitive generators, all possible serial and parallel arrangements of the primitive generators so that the resulting manipulator has the desired end-effector motion type were found. Using the formalism of [15] , we find that a mechanism is con- ditionally equilibrated with respect to an external force if the mechanism considering the passive joints only, is a motion generator of a motion for which the reciprocal product with the external force vanishes. Thus, while [15] uses the general concept of motion type (reference frame not specified) in their definition of motion generator, we will use a motion defined in a specific coordinate frame in our definitions. This allows us to verify resistance with respect to a specific external force, as opposed to a type or class of forces.
2. Preliminaries
This section presents a brief overview of mathematical modelling of rigid body motion and the definition of motion type. For a detailed treatment of the topic, the reader is referred to Murray et al. [4] , Meng et al. [15] , and From et al. [16] .
2.1. Rigid Body Motion
The special Euclidean group 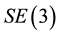 represents the configuration space of a rigid body. In addition to its group structure,
represents the configuration space of a rigid body. In addition to its group structure, 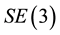 is a differentiable manifold, and is what is known as a Lie group.
is a differentiable manifold, and is what is known as a Lie group. 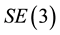 as a matrix Lie group can be written by homogeneous coordinates
as a matrix Lie group can be written by homogeneous coordinates
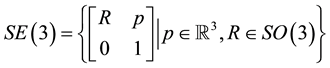 (1)
(1)
where 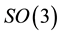 is the 3-dimensional special orthogonal group. An element
is the 3-dimensional special orthogonal group. An element 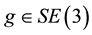 represents a rotation and a displacement of a rigid body relative to a reference configuration. Associated with every Lie group
represents a rotation and a displacement of a rigid body relative to a reference configuration. Associated with every Lie group  is its Lie algebra
is its Lie algebra 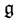 which is defined as the tangent space of
which is defined as the tangent space of 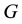 at the identity
at the identity  and is written as
and is written as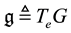 . The Lie algebra
. The Lie algebra 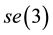 of
of 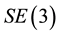 consists of all
consists of all 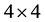 matrices
matrices
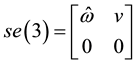 (2)
(2)
where ![]() and
and ![]() is the skew-symmetric matrix representation of
is the skew-symmetric matrix representation of ![]() given by
given by
![]() (3)
(3)
An element of ![]() can be represented by the twist coordinates
can be represented by the twist coordinates ![]() which can be iden-
which can be iden-
tified with the twist ![]() by the map1
by the map1
![]() (4)
(4)
Let Q be the configuration space of the constrained system. In our case ![]() so an element
so an element ![]()
can be represented by![]() . Then
. Then ![]() defines the set of allowed velocities of the constrained system at
defines the set of allowed velocities of the constrained system at![]() . We will write an element of the constraint forces as
. We will write an element of the constraint forces as![]() . The set of constraint forces
. The set of constraint forces
at ![]() is then defined as the vanishing of the reciprocal product with
is then defined as the vanishing of the reciprocal product with![]() , i.e.
, i.e.
![]() (5)
(5)
where![]() .
.
Denote by Lg and Rg the left and right translation maps, respectively. The differential ![]() of
of ![]() defines the body velocity and the differential
defines the body velocity and the differential ![]() of
of ![]() defines spatial2 velocity of a rigid body. Then for a trajectory
defines spatial2 velocity of a rigid body. Then for a trajectory![]() , the body velocity of the rigid body is given by
, the body velocity of the rigid body is given by
![]() (6)
(6)
while the spatial velocity is given by![]() . The body and spatial velocities are related by the Adjoint map
. The body and spatial velocities are related by the Adjoint map
![]() (7)
(7)
where ![]() and
and
![]() . (8)
. (8)
For a robotic mechanism with several sub-chains![]() , we will write the twist of joint
, we will write the twist of joint ![]() as
as ![]() and the twist system of chain
and the twist system of chain ![]() as
as
![]() (9)
(9)
where we use the second notation ![]() when we need to clarify what chain the joints belong to in a parallel mechanism. We use the same notation for the joint positions, i.e.
when we need to clarify what chain the joints belong to in a parallel mechanism. We use the same notation for the joint positions, i.e.![]() . The twist system describes the motion of the end effector for the open chain.
. The twist system describes the motion of the end effector for the open chain.
Let the parallel manipulator
![]() (10)
(10)
consist of ![]() serial manipulator sub-chains that share a common base and a common end effector. The set of end-effector motions is defined as [15]
serial manipulator sub-chains that share a common base and a common end effector. The set of end-effector motions is defined as [15]
![]() (11)
(11)
where ![]() is the set of rigid transformations that the subchain
is the set of rigid transformations that the subchain ![]() generates without loop constraints.
generates without loop constraints. ![]() defines the configurations of the end effector with the loop constraints imposed.
defines the configurations of the end effector with the loop constraints imposed.
We are interested in the passive motion, i.e. the motion due to the passive joints when the active joints are fixed. We denote this by
![]() (12)
(12)
where ![]() consists of only the passive joints of chain
consists of only the passive joints of chain![]() .
.
Although only the passive joints are considered, the twists of the passive joints depend on the configuration of the active joints. The twist of joint ![]() is given by
is given by
![]() (13)
(13)
where ![]() is the transformation from the base to joint
is the transformation from the base to joint![]() . We will assume it implicitly understood that the twists, as written in (9), are transformed according to (13), and thus write
. We will assume it implicitly understood that the twists, as written in (9), are transformed according to (13), and thus write ![]() for
for![]() . Similarly when we write
. Similarly when we write![]() , we mean
, we mean
![]() (14)
(14)
2.2. Motion Type
We now define motion type as in Meng et al. [15] . Motion type describes a class of motions, that is the con- jugacy class of a normal form subgroup or submanifold of ![]() under the similarity transformation.
under the similarity transformation.
Definition 2.1. The group of similarity transformations of![]() , denoted
, denoted![]() , consists of matrices of the form
, consists of matrices of the form
![]() (15)
(15)
Under the group of similarity transformations, helical motion with distinct pitches belong to the same conjugacy class. This is desirable in the definition of motion type as defined in [15] . We will need the following definition from Meng et al. [15] .
Definition 2.2. Let ![]() be a mechanism that consists of a system of coupled rigid bodies, one of which is identified with the base and one as the end-effector. Choose a reference configuration of
be a mechanism that consists of a system of coupled rigid bodies, one of which is identified with the base and one as the end-effector. Choose a reference configuration of ![]() and identify the joint variables with zero. Attach a coordinate frame to the end-effector and denote by
and identify the joint variables with zero. Attach a coordinate frame to the end-effector and denote by ![]() the set of rigid motions generated (or attainable) by the end-effector relative to the reference configuration, i.e.
the set of rigid motions generated (or attainable) by the end-effector relative to the reference configuration, i.e.![]() . Let
. Let ![]() be a normal form subgroup or submanifold of
be a normal form subgroup or submanifold of ![]() and
and![]() , the conjugacy class of
, the conjugacy class of ![]() under
under![]() .
. ![]() is said to have the motion type (or finite motion property) of
is said to have the motion type (or finite motion property) of ![]() if there exists
if there exists ![]() such that
such that ![]() agrees with
agrees with ![]() in an open neighbourhood
in an open neighbourhood ![]() of
of![]() , i.e.
, i.e.
![]() (16)
(16)
Equivalently we can write
![]() (17)
(17)
We are now ready to give the conditions for which serial and parallel manipulators have the motion type of Q.
Definition 2.3. We will denote a serial manipulator ![]() a motion generator of a subgroup or submanifold
a motion generator of a subgroup or submanifold ![]() of
of ![]() if
if ![]() contains an open neighbourhood of e in Q. If Q is a subgroup3 of
contains an open neighbourhood of e in Q. If Q is a subgroup3 of![]() , then
, then ![]() is a motion generator of
is a motion generator of ![]() if there exists a configuration such that
if there exists a configuration such that![]() .
.
For parallel manipulators the corresponding definition of a Parallel Motion (PM) generator is given by
Definition 2.4. A parallel manipulator ![]() is a Parallel Motion (PM) generator of
is a Parallel Motion (PM) generator of ![]() if there exists an open neighbourhood U of
if there exists an open neighbourhood U of ![]() in
in ![]() such that
such that![]() , where
, where![]() .
.
The conditions for which ![]() is a PM generator of the subgroup
is a PM generator of the subgroup ![]() is given in the following proposition [15] :
is given in the following proposition [15] :
Theorem 2.1. Given a motion type![]() . Assume that each
. Assume that each ![]() contains a connected open subset
contains a connected open subset ![]() of
of ![]() around
around![]() ,
,
![]() (18)
(18)
and consequently![]() . If the following condition
. If the following condition
![]() (19)
(19)
or the dual condition
![]() (20)
(20)
holds, where
![]() (21)
(21)
denotes the set of constraint forces for![]() , then,
, then, ![]() is a PM generator of
is a PM generator of![]() .
.
Proof. The proof is given in [15] . □
In the setting of this paper the following is also important. If for every![]() ,
,
![]() (22)
(22)
or its dual holds, then there exists a connected open subset ![]() of
of ![]() around
around ![]() such that
such that![]() , i.e.
, i.e. ![]() agrees with
agrees with ![]() in
in![]() .
.
Thus, alternatively we can write (19) in the transformed form as
![]() (23)
(23)
3. Equilibrated and Conditionally Equilibrated Serial and Parallel Manipulators
A parallel manipulator for which the mobility of ![]() is zero, can resist any external force. Specifically, we will denote a mechanism equilibrated if the following is satisfied:
is zero, can resist any external force. Specifically, we will denote a mechanism equilibrated if the following is satisfied:
Definition 3.1. A parallel manipulator ![]() is denoted equilibrated if
is denoted equilibrated if![]() , either through kinematic con-
, either through kinematic con-
straints or through actuator torques, can resist an arbitrary external wrench![]() . In the case
. In the case
that an arbitrary wrench can be accommodated by the kinematic constraints, we will say that the manipulator is passively sustained. When an arbitrary wrench can be produced by the actuation torque, we will denote it actively equilibrated.
A parallel manipulator is equilibrated with respect to an arbitrary wrench if and only if the mobility is equal to zero. To guarantee fault tolerance the mobility needs to remain zero when torque failure occurs for an arbitrary joint. This will require redundant actuators to be implemented. We note that a serial manipulator with passive joints can never be equilibrated.
When the mobility is not zero, the best result we can obtain is that the mechanism is conditionally equili- brated with respect to a given external wrench. This applies both to serial and parallel manipulators.
Definition 3.2. A manipulator ![]() is denoted conditionally equilibrated with respect to a given external wrench
is denoted conditionally equilibrated with respect to a given external wrench![]() , if
, if![]() , either through kinematic constraints or through actuator torques, can produce a wrench opposite to
, either through kinematic constraints or through actuator torques, can produce a wrench opposite to![]() , i.e.
, i.e. ![]() can produce the wrench
can produce the wrench ![]() for some
for some![]() .
.
Note that in this case we do not require that the manipulator can resist any external wrench, only that it can produce a wrench of a given type and direction. This can for example be used to verify if a mechanism can resist forces in the direction of the gavitational forces, but not necessarily gravitational forces of an arbitrary magnitude.
We see that we will need a different definition of motion than the one given in Section 2. While Definition 2.2 requires the existence of some![]() , we need to check for stability of an external force in one given direction, i.e. an external disturbance fixed in one given frame. Hence, we will define motion, as opposed to motion type, as all
, we need to check for stability of an external force in one given direction, i.e. an external disturbance fixed in one given frame. Hence, we will define motion, as opposed to motion type, as all ![]() that agree with
that agree with ![]() for a specific
for a specific![]() .
.
Definition 3.3. Let ![]() be a normal form subgroup or submanifold of
be a normal form subgroup or submanifold of ![]() and
and ![]() the homogeneous transformation of
the homogeneous transformation of ![]() for a given
for a given![]() .
. ![]() is said to have the motion of
is said to have the motion of ![]() if
if ![]() agrees with
agrees with ![]() in an open neighbourhood
in an open neighbourhood ![]() of
of![]() , i.e.
, i.e.
![]() (24)
(24)
or equivalently
![]() (25)
(25)
Note that ![]() is a motion type while
is a motion type while ![]() determines in what coordinate frame the motion is given, i.e. the “direction” of the motion. Hence, like
determines in what coordinate frame the motion is given, i.e. the “direction” of the motion. Hence, like ![]() in Definition 2.2,
in Definition 2.2, ![]() is a motion type. However, while
is a motion type. However, while ![]() (in Definition 2.2) is the conjugacy class of
(in Definition 2.2) is the conjugacy class of ![]() under
under![]() ,
, ![]() is a homogeneous transformation of
is a homogeneous transformation of ![]() under
under![]() . We then get the following important result.
. We then get the following important result.
Definition 3.4. A manipulator ![]() is conditionally equilibrated with respect to external forces
is conditionally equilibrated with respect to external forces ![]() if and only if
if and only if ![]() is not a motion generator of any component of
is not a motion generator of any component of![]() , i.e.
, i.e. ![]() is a motion generator of some
is a motion generator of some ![]() where
where![]() . We write this as
. We write this as![]() .
.
Thus we want the mechanism ![]() to generate the required motion
to generate the required motion ![]() and at the same time we want the passive mechanism
and at the same time we want the passive mechanism ![]() to generate motions that lie in
to generate motions that lie in![]() . We can summarise this as follows:
. We can summarise this as follows:
To get the desired properties for a parallel manipulator, we choose ![]() such that
such that
・ ![]() is a motion generator of (the motion type)
is a motion generator of (the motion type)![]() ,
,
・ ![]() is a motion generator of (the motion)
is a motion generator of (the motion)![]() .
.
When joint failure occurs in a parallel mechanism we want the second property to remain true. We note that ![]() includes both passive and active joints and will thus not change if torque failure occurs.
includes both passive and active joints and will thus not change if torque failure occurs.![]() , however, will change and therefore, to guarantee fault tolerance, the mobility of
, however, will change and therefore, to guarantee fault tolerance, the mobility of ![]() must be checked against joint failure in all joints. If the manipulator allows any motion we need to look into if we can guarantee that the mechanism remains conditionally stable with respect to a given external force.
must be checked against joint failure in all joints. If the manipulator allows any motion we need to look into if we can guarantee that the mechanism remains conditionally stable with respect to a given external force.
For parallel manipulators we start the analysis by finding the mobility ![]() considering the passive joints only. If the mobility of the mechanism is zero we can conclude that the mechanism is equilibrated with respect to any external force. Mobility in the setting of fault tolerance is discussed briefly in Section 4, and examples are given in From and Gravdahl [14] . On the other hand, if the mobility
considering the passive joints only. If the mobility of the mechanism is zero we can conclude that the mechanism is equilibrated with respect to any external force. Mobility in the setting of fault tolerance is discussed briefly in Section 4, and examples are given in From and Gravdahl [14] . On the other hand, if the mobility ![]() for parallel manipulators and similarly for serial manipulators with passive joints, an additional condition needs to be satisfied for the mechanism to be equilibrated. The requirement for which
for parallel manipulators and similarly for serial manipulators with passive joints, an additional condition needs to be satisfied for the mechanism to be equilibrated. The requirement for which ![]() is conditionally equilibrated is treated in Section 5 for serial manipulators and Section 6 for parallel manipulators together with several examples.
is conditionally equilibrated is treated in Section 5 for serial manipulators and Section 6 for parallel manipulators together with several examples.
4. Fault Tolerance
In this section, we look into the effect of free-swinging joint failure (FSJF), or torque failure, in parallel mani- pulators and in particular how the results found in From and Gravdahl [14] can be used to prevent that the mechanism turns unequilibrated when this occurs. For a general treatment and an approach on how to identify joint failure see [10] In this case, as the number of passive joints in the manipulator increases by one, the mobility of ![]() may remain zero or increase by one. Let
may remain zero or increase by one. Let ![]() be the number of active joints in
be the number of active joints in![]() . When
. When ![]() does not allow any motion after the joint failure, we have
does not allow any motion after the joint failure, we have
![]() (26)
(26)
and the mechanism remains equilibrated with respect to all external forces. When ![]() allows a 1 DOF motion as a result of the joint failure, i.e.
allows a 1 DOF motion as a result of the joint failure, i.e.
![]() (27)
(27)
the mechanism is not fault tolerant. In this case the mechanism can at best be conditionally equilibrated, this is discussed in the remainder of the paper.
5. Robustness to External Forces for Serial Manipulators
The results presented in Section 2 let us quickly verify if a given serial or parallel manipulator has the desired type of end-effector motion. We will now use the same approach to analyse if a manipulator allows an undesired motion due to passive joints. We will start with a motivating example for the serial case.
Example 5.1. Consider a serial manipulator with one passive revolute joint at the end of the manipulator chain in Figure 1.
Attach a coordinate frame at the base of the manipulator and choose the reference configuration so that the revolute axis of the last joint and the ![]() -axis of the inertial frame are parallel. Assume that the joint revolutes about the
-axis of the inertial frame are parallel. Assume that the joint revolutes about the ![]() -axis with unit velocity, i.e.
-axis with unit velocity, i.e.![]() , and let
, and let ![]() be a point on the
be a point on the ![]() -axis
-axis
![]() . Then the twist is given by
. Then the twist is given by
![]() (28)
(28)
Assume further two external (linear) forces
![]() (29)
(29)
![]()
Figure 1. A serial manipulator with one passive re- volute joint at the end of the manipulator chain.
For the chosen reference configuration the set of constraint forces for the twist ![]() is given by all forces
is given by all forces ![]() that satisfy
that satisfy![]() , and we conclude that
, and we conclude that
![]() (30)
(30)
Thus, for the twist describing a joint that revolutes about the ![]() -axis and an external force
-axis and an external force ![]() the reciprocal product vanishes and the joint is not affected by the external force
the reciprocal product vanishes and the joint is not affected by the external force![]() . For a force in the direction of the
. For a force in the direction of the ![]() - axis, however, this is not the case and the configuration of the last joint is affected by this external force. We see that for a serial manipulator the set of external forces for which the passive joint maintains its posture is, as already noted, very limited.
- axis, however, this is not the case and the configuration of the last joint is affected by this external force. We see that for a serial manipulator the set of external forces for which the passive joint maintains its posture is, as already noted, very limited.
From the simple example presented above, we see that the end-effector configuration is equilibrated with respect to one “type” or group of external forces, but not to others. We will denote the mechanism conditionally equilibrated when it is equilibrated with respect to a specific type of external force, e.g. gravity. In the following we will generalise this using the formalism presented in Meng et al. [15] .
We will restrict ourselves to![]() , i.e. linear forces and the moments that result from these. The extension to
, i.e. linear forces and the moments that result from these. The extension to ![]() is straight forward. This is for example the case when the base moves with an angular velocity, for example ships or a moving vehicle (From et al. [17] ).
is straight forward. This is for example the case when the base moves with an angular velocity, for example ships or a moving vehicle (From et al. [17] ).
Example 5 is special in the sense that the axis of the passive joint is constant. This is obviously not always the case, for example when the passive joint is at the end of a manipulator chain. Thus, we will divide the problem into two parts: 1) when the mechanism is locally equilibrated (at reference configuration); and 2) when the mechanism is globally equilibrated (for any position of the active joints). A mechanism can be equilibrated with respect to an external disturbance for one configuration but not for another. We will start by looking at the local case and look at how external disturbances affect the mechanism at the reference configuration. In Section 5.2 we will extend this to the entire workspace of the manipulator.
5.1. A Local Solution
To analyse the manipulator when it is in the reference configuration is very much related to the work presented in [15] , and their results can be applied with a few simple modifications. From Example 5 we see that another definition of motion than the one given in Definition 2.2 is needed. We need to define the motion with respect to a given reference frame.
Thus, for a given external wrench, the equilibrated motion represents all the “directions” in which we can allow the manipulator to move, i.e. the directions that are not affected by the external force. This is formalised in the following.
Definition 5.1. For a given nominal external wrench ![]() the set of equilibrated motions is defined as all twists for which the reciprocal product with
the set of equilibrated motions is defined as all twists for which the reciprocal product with ![]() vanishes, i.e.
vanishes, i.e.
![]() (31)
(31)
We see that ![]() gives us a complete description of all the motions the mechanism can generate and still be conditionally equilibrated with respect to the external wrench. The complete description of the equilibrated motion is then given by choosing the external wrench F0 represented in the inertial frame, i.e. the type of the dis- turbance, and the coordinate frame
gives us a complete description of all the motions the mechanism can generate and still be conditionally equilibrated with respect to the external wrench. The complete description of the equilibrated motion is then given by choosing the external wrench F0 represented in the inertial frame, i.e. the type of the dis- turbance, and the coordinate frame ![]() of
of ![]() and we write
and we write![]() . Similarly, we get
. Similarly, we get![]() .
.
Assume now a manipulator with ![]() joints, which of
joints, which of ![]() are passive. Without loss of generality we assume that the passive joints are at the end of the manipulator chain. We denote by
are passive. Without loss of generality we assume that the passive joints are at the end of the manipulator chain. We denote by ![]() the
the ![]() first active joints and by
first active joints and by ![]() the last
the last ![]() passive joints of the manipulator, so we have
passive joints of the manipulator, so we have
![]() (32)
(32)
For a mechanism to be resistant to an external force it can only allow motions in![]() . From this observation and the fact that active joints themselves are always equilibrated with respect to external forces, we conclude the following:
. From this observation and the fact that active joints themselves are always equilibrated with respect to external forces, we conclude the following:
Definition 5.2. Given ![]() and a corresponding equilibrated motion
and a corresponding equilibrated motion![]() . A serial manipulator
. A serial manipulator ![]() is equilibrated with respect to external forces
is equilibrated with respect to external forces ![]() if and only if
if and only if ![]() generates a motion
generates a motion![]() .
.
This becomes clearer with the following proposition:
Proposition 5.1. Let ![]() and
and ![]() so that each
so that each ![]() represents the twist of joint
represents the twist of joint ![]() and the
and the![]() ’s are
’s are ![]() external forces. Then
external forces. Then ![]() is conditionally equilibrated with respect to
is conditionally equilibrated with respect to ![]() if and only if
if and only if
![]() (33)
(33)
This proposition states that the external force must lie in the constraint motion of each joint and that each joint can be looked at independently. We will write this on a more compact form as
![]() . (34)
. (34)
We will say that when Equation (34) is satisfied, ![]() is conditionally equilibrated with respect to all external forces in
is conditionally equilibrated with respect to all external forces in![]() .
.
5.2. A Global Solution
The results presented in the previous section give a simple condition for the mechanism to be equilibrated with respect to an external force around the reference configuration. We now expand this to the entire workspace, i.e. for what positions of the active joints is the mechanism conditionally equilibrated. We start with a simple example.
Example 5.2. Assume we want to check if a mechanism is equilibrated with respect to the gravitational forces, i.e.![]() . Let the last passive joint revolute around the inertial
. Let the last passive joint revolute around the inertial ![]() -axis at reference con- figuration Figure 2.
-axis at reference con- figuration Figure 2.
We have
![]() (35)
(35)
Then the problem amounts to finding all configurations ![]() for which
for which
![]() (36)
(36)
where
![]() (37)
(37)
where ![]() means
means ![]() and
and ![]() means
means![]() .
.
The solution is obtained by a rotation ![]() around the
around the ![]() -axis. We see that the mechanism is equilibrated
-axis. We see that the mechanism is equilibrated
with respect to forces working in the same direction as the axis of the revolute joint only. Note in addition to these there are certain positions of the passive joint for which the external forces do not affect the configuration,
![]()
Figure 2. A serial manipulator with one passive re- volute joint at the end of the manipulator chain.
such as the stable and unstable equilibrium of a pendulum, but we require that the mechanism can resist external forces for all positions in order to denote it conditionally equilibrated and isolated points in the configuration space are thus not included in the solution.
For serial manipulators the formulation described can give us a restriction on the configuration of the last “active link” for the manipulator to be conditionally equilibrated. By last active link we mean the link after the last active joint. This is formalized in the following.
A transformation from the reference configuration to a joint can be given as a rigid transformation ![]() by the Adjoint map
by the Adjoint map![]() . We will introduce the following notation
. We will introduce the following notation ![]() which describes the twists of the passive joints under the influence (rigid transformation) of the active joints. Hence,
which describes the twists of the passive joints under the influence (rigid transformation) of the active joints. Hence,
![]() (38)
(38)
where ![]() is the rigid transformation from the base to joint
is the rigid transformation from the base to joint ![]() and thus depends on the joint positions. Further we will assume that the passive joint, if equilibrated at the reference configuration, is equilibrated for all posi- tions of the passive joint. Note that we can only control the position of the active joints
and thus depends on the joint positions. Further we will assume that the passive joint, if equilibrated at the reference configuration, is equilibrated for all posi- tions of the passive joint. Note that we can only control the position of the active joints ![]() while the position of the passive joints
while the position of the passive joints ![]() can move freely. An example is given in the next section.
can move freely. An example is given in the next section.
5.3. Free Swinging Joint Faults in Serial Manipulators
For a serial manipulator free-swinging joint fault is extremely serious and will in general cause the manipulator to collapse, or at least lose its controllability. This can cause damage both to humans and the surroundings. In this case we will need an additional requirement on the active joint positions so that the manipulator is condi- tionally equilibrated.
Definition 5.3. A serial manipulator ![]() is conditionally equilibrated with respect to an external force
is conditionally equilibrated with respect to an external force ![]() (e.g. gravity) if and only if the active joints
(e.g. gravity) if and only if the active joints ![]() are chosen such that
are chosen such that
![]() (39)
(39)
When joint failure occurs for any of the joints close to the base, this requirement is practically impossible to satisfy. Due to the kinematics of many commonly used manipulators such as the Motoman DIA or ABB IRB, this condition is, on the other side, quite easy to satisfy when the joint error occurs for one of the last joints. Examples of this are given below.
Example 5.3. Assume a manipulator with one active and one passive revolute joint and where the passive joint is parallel to the disturbance (gravity) ![]() at reference configuration. We have
at reference configuration. We have
![]() (40)
(40)
We are to verify under what condition, i.e. for what configurations of![]() , the mechanism remains equili- brated. We will consider two cases
, the mechanism remains equili- brated. We will consider two cases
・ when the active joint rotates about the ![]() -axis Figure 3,
-axis Figure 3,
・ when the active joint rotates about the ![]() -axis Figure 4.
-axis Figure 4.
In both cases, the twist of the passive joint is written as
![]() (41)
(41)
![]()
Figure 3. A serial manipulator with one active and one passive revolute joint.
![]()
Figure 4. A serial manipulator with one active and one passive revolute joint.
The rotational and translational displacements due to the active joint in the two cases are given by
![]()
![]()
where ![]() means
means ![]() and
and ![]() means
means![]() . For the first case when the active joint is parallel to the disturbance,
. For the first case when the active joint is parallel to the disturbance, ![]() is given by
is given by
![]()
and we get that
![]() (42)
(42)
As (39) is always satisfied, the mechanism is equilibrated for all configurations and no further action is required.
For the second case, we have
![]()
and we get that
![]() (43)
(43)
We see that in the second case, the manipulator is conditionally equilibrated with respect to Fext if and only if
![]() (44)
(44)
This is the case when![]() , which is the reference configuration and when
, which is the reference configuration and when ![]() which is when the first link points in the exact opposite direction of the reference configuration. Thus, if joint failure occurs, we should strive to reach one of the configurations represented by
which is when the first link points in the exact opposite direction of the reference configuration. Thus, if joint failure occurs, we should strive to reach one of the configurations represented by
![]() (45)
(45)
in order to minimise damage to the surroundings.
Example 5.4. Assume a manipulator with two active (![]() - and
- and ![]() -axes in reference configuration) and one passive (
-axes in reference configuration) and one passive (![]() -axis) joint in Figure 5.
-axis) joint in Figure 5.
In this case the set of equilibrated configurations![]() , is given by
, is given by
![]() (46)
(46)
![]()
Figure 5. A serial manipulator with two active (z- and y-axes in reference configuration) and one passive (z- axis) joint.
We see that the stability depends on the position of ![]() while the position of
while the position of ![]() can be chosen freely.
can be chosen freely.
6. Robustness to External Forces for Parallel Manipulators
From From and Gravdahl [14] and Section 4, we learned that when ![]() does not allow any motion after the joint failure, i.e. we have
does not allow any motion after the joint failure, i.e. we have![]() , the mechanism is passively sustained with respect to any external force. However, when the mechanism allows a motion due to the joint failure, i.e.
, the mechanism is passively sustained with respect to any external force. However, when the mechanism allows a motion due to the joint failure, i.e.
![]() (47)
(47)
an additional requirement needs to be satisfied for the mechanism to be equilibrated. In this case the mechanism cannot be equilibrated with respect to an arbitrary external force, as there will always exist a force that results in the free motion. Thus, the strongest result we can obtain in this case is to guarantee that the mechanism is passively sustained with respect to a given external force.
As for the serial case, we get that this is true when the allowed motion lies in the annihilating space of the external forces. Finally we look at the global case and find for what configurations, i.e. positions of the active joints, this is true.
6.1. A Local Solution
Again we start by choosing a reference configuration and identify the joint positions with zero. In this section we apply the same modifications to the results presented in [15] as for serial manipulators. Recall that our definition of motion differs from the definition of motion type in [15] in that ![]() relates to
relates to ![]() by a (specific) homogeneous transformation and not by the conjugacy class of the similarity transformation. We need to verify if the constrained motion of the end effector
by a (specific) homogeneous transformation and not by the conjugacy class of the similarity transformation. We need to verify if the constrained motion of the end effector ![]() lies in the equilibrated motion
lies in the equilibrated motion![]() . We thus assume that each
. We thus assume that each ![]() contains a connected open subset
contains a connected open subset ![]() of
of ![]() around
around![]() ,
,
![]() (48)
(48)
and consequently,![]() . Due to the kinematic constraints, the configuration space of the end effector is forced to be
. Due to the kinematic constraints, the configuration space of the end effector is forced to be
![]() (49)
(49)
Recall that ![]() represents the equilibrated motions with respect to
represents the equilibrated motions with respect to ![]() represented in the coordinate frame
represented in the coordinate frame![]() .
.
Proposition 6.1. Let ![]() be the equilibrated motion with respect to
be the equilibrated motion with respect to![]() . The parallel manipulator
. The parallel manipulator ![]() is resistant to the external forces
is resistant to the external forces ![]() if
if ![]() is contained in
is contained in![]() , i.e.
, i.e.
![]() (50)
(50)
Alternatively we can verify that ![]() is contained in the constraint forces of
is contained in the constraint forces of![]() , i.e.
, i.e.
![]() (51)
(51)
holds, which means that every component of ![]() is restrained by the constraint forces of
is restrained by the constraint forces of![]() .
.
This guarantees that the end-effector motion is not affected by the external forces. Note that we also have to check for the internal motion of each chain. Hence, if joint failure occurs in chain![]() , we also need to verify that the internal motion of this chain is contained in
, we also need to verify that the internal motion of this chain is contained in![]() .
.
6.2. A Global Solution
In this section we generalise the results from the previous section to find all configurations for which the mecha- nism is conditionally equilibrated with respect to a given external force. We will first assume that all the passive joints are at the end of the sub-chains
![]() (52)
(52)
Again we need to verify if the mechanism, considering the passive joints only, is equilibrated with respect to an external force![]() . We denote the transformation of
. We denote the transformation of ![]() by the active joints as
by the active joints as![]() . We then need to find the set
. We then need to find the set
![]() (53)
(53)
where
![]() (54)
(54)
is the attainable spatial velocities of ![]() at
at ![]() and
and ![]() is the equilibrated motion with respect to
is the equilibrated motion with respect to ![]() in a given reference frame
in a given reference frame![]() .
.
The main observation here is that the infinitesimal motions attainable by![]() , when
, when ![]() is at the end of the chains, are transformed by a rigid transformation
is at the end of the chains, are transformed by a rigid transformation ![]() which depends on the active joints only. Thus, we can write
which depends on the active joints only. Thus, we can write
![]() (55)
(55)
and we can use ![]() for
for ![]() in Equation (50).
in Equation (50).
We will divide the motion of the mechanism into two motions. First, ![]() is the motion due to the passive joints. This motion is affected by the external disturbances. The other motion is
is the motion due to the passive joints. This motion is affected by the external disturbances. The other motion is ![]() which is due to the active joints. This is not affected by the external disturbance. The aim of this section is to find the configurations of the active joints so that
which is due to the active joints. This is not affected by the external disturbance. The aim of this section is to find the configurations of the active joints so that![]() .
.
We will write
![]() (56)
(56)
where ![]() is the transformation from the base to joint
is the transformation from the base to joint ![]() of chain
of chain![]() . In the previous sections the active joints were considered fixed. Now, the direction of the twists of the passive joints will depend on the position of the active joints, i.e.
. In the previous sections the active joints were considered fixed. Now, the direction of the twists of the passive joints will depend on the position of the active joints, i.e. ![]() depends on the position of the active joints.
depends on the position of the active joints.
We need to verify if
![]() (57)
(57)
where ![]() and
and![]() . We will represent the set of conditionally equilibrated configurations as
. We will represent the set of conditionally equilibrated configurations as
![]() (58)
(58)
which is found by
![]() (59)
(59)
which is the set of all equilibrated configurations for![]() .
.
6.3. Free Swinging Joint Faults in Parallel Manipulators
Free swinging joint faults affect parallel manipulators differently than serial manipulators. For serial manipula- tors joint faults is extremely serious while this is not always the case for closed chain manipulators due to the kinematic constraints. In this section we present several examples illustrating the effects of torque failure in pa- rallel mechanisms.
Consider the parallel manipulator in Figure 6. We consider two cases when joint failure occurs in![]() ;
;
・ the actuated joints are chosen as in Figure 6,
・ the actuated joints are chosen as in Figure 6 but with ![]() actuated instead of
actuated instead of![]() .
.
Example 6.1. Assume that the actuated joints are chosen as in Figure 6 and joint failure occurs in![]() . We choose a reference configuration as in Figure 6 and the twists of each chain is given by
. We choose a reference configuration as in Figure 6 and the twists of each chain is given by
![]() (60)
(60)
and we get
![]() (61)
(61)
Thus for the chosen reference configuration, ![]() is not conditionally equilibrated with respect to the gravitational forces. It is, however, conditionally equilibrated with respect to all forces in the
is not conditionally equilibrated with respect to the gravitational forces. It is, however, conditionally equilibrated with respect to all forces in the ![]() -plane, e.g.
-plane, e.g.
![]()
We now look into for what configurations this is true. This is straight forward due to the observation
![]() (62)
(62)
and thus the twists of the passive joints are independent of positions of the active joints. The set of joint posi- tions for which the manipulator is conditionally equilibrated with respect to ![]() is thus given by
is thus given by
![]() (63)
(63)
Similarly, the set of joint positions for which the manipulator is conditionally equilibrated with respect to ![]() is thus given by
is thus given by
![]() (64)
(64)
Example 6.2. Again we assume that the actuated joints are chosen as in Figure 6 and joint failure occurs in![]() , but with
, but with ![]() actuated instead of
actuated instead of![]() . We choose a reference configuration as in Figure 6 and the twists of each chain is given by
. We choose a reference configuration as in Figure 6 and the twists of each chain is given by
![]() (65)
(65)
and we get
![]() (66)
(66)
Thus for the chosen reference configuration, ![]() is conditionally equilibrated with respect to the gravi- tational forces only, e.g.
is conditionally equilibrated with respect to the gravi- tational forces only, e.g.
![]()
We now look into for what configurations this is true. Again we have that Equation (62) is true and that the twists of the passive joints are independent of positions of the active joints. The set of joint positions for which the manipulator is conditionally equilibrated with respect to ![]() is thus given by
is thus given by
![]() (67)
(67)
Similarly, the set of joint positions for which the manipulator is conditionally equilibrated with respect to ![]() is thus given by
is thus given by
![]() (68)
(68)
This example illustrates the difference between the effects of joint failure in serial and parallel manipulators. For serial manipulators we can often take the manipulator to a certain configuration for which it is conditionally equilibrated. For parallel manipulators, however, we find that this requirement is either satisfied for all con- figurations, as in (67), or it is not satisfied at all, as in (68). Thus, if the parallel mechanism is conditionally equilibrated, this is an intrinsic property of the mechanical design and only in very special cases can it be taken care of in the control. For serial manipulators, however, the design of the manipulator does affect the condition to a certain extent, but we have more freedom to deal with external disturbances in the control when joint failure occurs.
7. Conclusions
A mathematically rigorous framework for analysing the effects of joint failure in serial and parallel manipulators is presented. For serial manipulators we find that for certain configurations the manipulator remains con- ditionally equilibrated with respect to a specific external force, such as gravity, even after joint failure occurs. This must thus be handled in the control algorithms as there is no way to guarantee fault tolerance through a fault tolerant design of the mechanism.
For parallel manipulators, however, we can find a set of active joints for which the design itself is fault tolerant. In this sense, the parallel manipulators are more robust than their serial counterparts. On the other hand, when actuator failure occurs and this allows for a motion in the passive joints, we have less flexibility to deal with this in the control algorithms than for serial manipulators. In general we find that the parallel manipulator is either conditionally equilibrated for all configurations, or it is never conditionally equilibrated. Fault tolerance of parallel manipulators should thus be addressed in the design of the mechanism.
NOTES
1For simplicity we will write twist for both twist coordinates and twists.
![]()
2In this context, spatial means that the velocity is given with respect to a globally defined coordinate system. We will also use spatial for the 3-dimensional space, as opposed to the 2-dimensional space.
![]()
3The case when ![]() is a submanifold of
is a submanifold of ![]() is treated in detail in [15] .
is treated in detail in [15] .