Determining Critical Submergence in Tanks by Means of Reynolds & Weber Numbers ()
1. Introduction
The physical problem under analysis is free fluid surface deformation, or to put it more clearly, the challenge is to explain how the separation surface of two immiscible fluids evolve under specific conditions. Narrowing it down even more, the actual issue is to do with the way in which tank drainage through a boundary nozzle deforms the surface of the liquid in the tank at atmospheric pressure.
Conceptually speaking, submergence refers to the level of liquid required above the suction section to avoid vortexing/swirls, hence preventing the entry of gas (air) that may affect pump operation in the form of cavitation, vibration and/or performance shortfalls.
Closer analysis of the problem reveals the role played by two additional processes: tank drainage and free fluid surface deformation. The first process, tank drainage, depends on fluid-related shear forces, nozzle size and outlet flow or velocity, with the Reynolds number (Equation (1)) and Froude number (Equation (2)) being the representative dimensionless numbers.
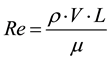 (1)
(1)
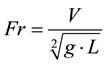 (2)
(2)
where:
“g” is the gravity acceleration.
“V” is fluid velocity at the outlet nozzle.
“L” is the representative dimension (outlet nozzle diameter in this case).
“µ” is dynamic fluid viscosity.
“r” is fluid density.
Free fluid surface deformation and vortexing is the other process, which is conditioned or determined by fluid surface tension. The dimensionless number for this process is the Weber number, considered very useful to analyze multiphase flows, curved surface flows, thin layer flows, as well as drop and bubble formation. It is re- presented as:
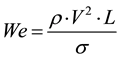 (3)
(3)
In this case, “V” is the velocity at which tank level decreases, “L” is the tank diameter and “σ” is the superficial stress.
It is possible to determine the critical submergence value using many formulas, some of which are included in Table 1.
![]()
Table 1. List including some of the most commonly used for- mulas for calculating critical submergence.
The previous table indicates that under identical velocity and diameter values, critical submergence varies and can be quite sparse, with oscillations ranging between 1 to 3.5 meters depending on the conditions. Under the same conditions abovementioned, vortexing occurred at 0.5 meters during a hydraulic model test. So in light of this uncertainty, the question is: Would it be possible to calculate critical submergence more accurately?
A rather promising piece of information is that in 2012, the University of Stellenborg tested a hydraulic model with the aim of comparing actual test results to formulations, including those in Table 1 and some additional ones based on experimental tables [7] . It was observed that vortexing height was similar to the data in KSB and Metcalf & Eddie and quite different to the calculated values; thus, the possibility of real adjustment is forecasted. A weakness of these tests is that only water was used, meaning that conclusions are only valid for one type of fluid (represented in Figure 1).
Another important topic is to physically determine submergence with the aim of standardizing the concept and performing subjectivity-free measurements and evaluations, especially in hydraulic model cases. Hence, submergence is related to a massive suction pump air entry affecting pump performance. If the possibility of cavitation is eliminated, air entering a suction line occurs due to vortexing, with the vortex vertex affecting pump suction and causing suction pressure and subsequently NPSH to be reduced. From this it is possible to conclude that submergence is related to vortexing, which results from free liquid surface deformation [8] .
Vortices are described and categorized depending on their morphology in a document by the Hydraulic Institute [1] . This classification can be seen in Figure 2.
![]()
Figure 1. Critical submergence (calculated and average).
![]()
Figure 2. Vortex typology according to the hydraulic institute.
In terms of operation and effectiveness, bubble-based phenomena will not be considered because bubble air, in small quantities, can be assimilated by the fluid and does result in significant performance losses. Besides, bubble behavior is very complicated to simulate using software packages and its analysis depends largely on observer subjectivity. Thus, type 5 vortex is discarded. As for superficial vortices, they have no impact on pump suction, which means type 1 and 2 vortices will not be considered. This all means that there are only three different types of vortices potentially impacting submergence: 3, 4 & 6. The first two do not imply air entry and so they are discarded because of their very morphological nature. Hence, submergence is conditioned by type 6 vortex. Critical submergence is determined when the type 6 vortex vertex reaches the upper part of the suction structure. In that moment, a massive entry of air occurs, as represented in Figure 3.
2. Methodology
The methodology used in this survey is based mostly on the use of numerical methods (CFD) to simulate the critical submergence level or height [9] [10] . This methodology is not purely numeric because to validate the numerical method, the number obtained through it and the hydraulic model test result, need to be compared.
Simulation conditions have taken into condition eleven suction scenarios, two fluids at different temperatures and six tank geometries. The cases can be seen in Table 2.
Numerical method validation will be based on cases 9, 10 and 11, for which there is a physical model. The assumption will be made that if the result is adequate and in line with the observations, the remaining simulations will be equally valid.
![]()
Figure 3. Type 6 vortex reaching the upper part of the outlet nozzle.
![]()
Table 2. Simulation and test conditions.
Once critical submergence results are determined by means of numerical methods, the above-mentioned process for canals with flow will be used to compare the resulting value to the dimensionless numbers of Reynolds and Weber [11] . For the purposes of this paper it is considered that the fluid is laterally confined and that lateral flow is impossible. The following equation illustrates this relationship:
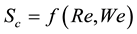 (4)
(4)
2.1. Determination of Dimensionless Numbers
Historically (Table 1) only the Froude number was considered to estimate critical submergence. A few studies on suction lines have used some other number, such as that of Reynolds. The number of Weber has rarely been used because its dependence only applies when fluids have different properties or when the surface tension of one of the fluids is heavily dependent on temperature. In some of the cases analyzed, the numbers of Reynolds and Weber have a lower value when associated to problems affecting one single liquid, at one single temperature or with a configuration in which the fluid in the suction area moves transversely (in the canals). As a result of this approach, only suction velocity, gravity acceleration and a characteristic length (outlet nozzle diameter), have been taken into consideration. Thus, this fundamental parameter and scheme does not take into account fluid properties (density, viscosity) or air-liquid interfaces (surface tension).
It may appear that this approach to the problem is completely opposite to the historical perspective, but that is certainly not the case. In fact, this approach is aimed at including fluid and interface variables developed using the Froude number in the formulations. However, since that would result in excessively complex formulas, additional dimensionless numbers are used. Equation (4) shows the equivalence between the dimensionless numbers introduced:
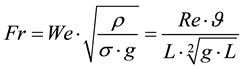 (5)
(5)
Another historical aspect to be considered is that Weber, Reynolds and Froude numbers were calculated using the same parameters, meaning the outlet nozzle diameter was always taken as the characteristic length. This paper intends to differentiate two processes impacting critical submergence calculation: (1) the effect of suction on liquid motion and (2) the effect of tank drainage. Free fluid surface deformation is the process relating both of them. Hence, the number of Reynolds (question 2) is related to suction, which means “V” will refer to fluid velocity in the outlet nozzle and “L” to outlet nozzle diameter. As for the number of Weber (Equation (3)), and taking into consideration that this concept is affected by surface tension, the diameter will be that of the tank, whereas the velocity will refer to how quickly the tank is drained (outlet flow divided by tank section).
These considerations result in the dimensionless number values included in Table 3.
![]()
Table 3. Dimensionless number values.
2.2. Numerical Method
The numerical method selected is a finite element scheme (described in previous studies) considered reliable and validated by the industry [12] . The differences between the physical properties and dimensions of the fluids (liquid and gas) determine the selection of the mathematical models to be used.
In order to ensure accurate simulation, it is essential to know if the flow is turbulent, and if so, to estimate the level of turbulence so as to determine mesh size. Another key aspect to consider is the free surface. Considering that movement is mostly vertical, that is, since liquid level will potentially decrease causing suction areas and vortexing near the outlet nozzle, it will be necessary to use large cells of reduced thickness in areas far from the nozzle and small cells (size and thickness) in areas near the nozzle (Figure 4).
Although meshing depends on the specific geometry of each tank, there are common features to be considered. The model is comprised mostly (85%) of hexahedral cells, as well as a very small percentage of tetraedric cells located mostly in the overlap area between the tank and the outlet nozzle. Mesh quality has been improved by means of a methodology intended to:
Transform tetraedric cells into polyhedral cells so as to reduce the number of cells and enhance mesh quality (Figure 5).
Protect the suction area in a semi-cylinder to limit the region where the cells of lower quality are located (Figure 6).
The mesh was also improved by making it thinner in the outlet nozzle than in the rest of the tank (Figure 7).
![]()
Figure 4. Different cell sizes in plant meshing.
![]()
Figure 5. Detailed picture of an enhanced mesh with polyhedral cells.
![]()
Figure 6. Detailed picture of a mesh with a semi-cylindrical area.
![]()
Figure 7. Detailed picture of the outlet nozzle and its mesh.
Once the mesh is determined, it is possible to establish the following simulation characteristics:
・ Single phase suction flow. (simulation until air entry)
・ K-ε turbulence model
・ Turbulence model for “Enhanced Wall Treatment” (EWT)
The K-ε model is intended for turbulent flows and vortexing. As for the EWT model, it provides an estimate for the film boundary layer, favoring mesh optimization near the walls.
The validation and control parameter for the model developed will be Y+, which is the distance between the first cell and the viscous film boundary layer. The value of the K-ε and the EWT should range between 1 and 60 for the simulation to be considered accurate and reliable. An example of this can be seen in the suction pipe of case 2, represented in Figure 8.
After describing the domain model the numerical value is strictly analyzed, that is, the differential equation governing this process is approached. The method selected is the Volume of Fluid (VOF) scheme, with numeri-
![]()
Figure 8. Y+ value limits in outlet nozzle.
cal discretization―modified HRIC. This model was selected to simulate tank drainage over a long period of time. In parallel and related to this, a resolution using an explicit model and numerical discretization―geo-re- construct, was also carried out. The calculation time in this method is much longer because the free surface is simulated more thoroughly.
Hence, the value of numerical discretizations of superior or second-order differential equations in the time domain is 0.1 seconds, with 30 iterations per time step. In this scheme the numeric error is below 10−4 for the velocity, continuity, and turbulence equations, and below 10−5 for the VOF equation. In the case of explicit free surface simulation, the time step is variable at about 0.0005 seconds with 20 iterations per time step.
As mentioned in previous paragraphs, the numerical model needs to be validated and calibrated using real values. With this in mind, the results of a hydraulic model for critical submergence determination developed for this specific purpose, were considered. The model included a tank, a suction line and a piping network. The entire installation was simulated using the above-mentioned numerical method. Table 4 shows the results associated to hydraulic model testing and simulation values. As can be seen, the data measured in the hydraulic lab and the value obtained using a definite element method, were very accurate, with a simulation error lower than 5%. Thus, this model is rendered highly representative. Therefore, the finite element method will be a sort of lab generating accurate submergence values suitable for usage in the development of adjustment equations.
3. Results
Considering the previously described methodology as well as the geometry of the tanks, fluids and suction pipes, critical submergence for each specific case was determined. The critical submergence value above the height or level of the last suction section was calculated. With the aim of ensuring analysis coherence and homogeneity between the different case scenarios, the zero determination applicable to the submergence measurement is as follows: In a straight outlet nozzle, submergence is measured at the upper nozzle generatrix whereas in a suction nozzle with an elbow or curved pipe, the zero value is considered to be in the elbow's upper generatrix of the suction point (Figure 9).
Under these considerations, two submergence values were determined: one for critical submergence (Sc) and the other for efficient submergence (Se) defined at the level where free liquid surface deformation equals 10%. The relevant values can be seen in Table 5.
Equation Adjustment
The selected adjustment process is a multivariate regression model including two inlet values corresponding to the dimensionless numbers (Re, We) and an outlet value for critical submergence. The process will be extended to the values of both effective submergence and critical submergence.
To determine critical submergence, which is the first value to be calculated, a second degree polynomial is used. The coefficients are determined by means of the regression process. Thus, the adjustment equation is that represented by Equation (6).
![]() (6)
(6)
![]()
Table 4. Comparison between the submergence calculation method (VOF) and the lab test.
1The reference for this calculation is taken at the bottom of the tank.
![]()
Table 5. Values for critical and effective submergence.
![]()
Figure 9. Schematic situation of effective and critical submergence
Using the data in Table 3 and Table 5, as well as a regression process (non-linear least squared method), the adjustment parameter values associated to Equation (6) are those included in Table 6.
The adjustment coefficient values in Table 6 are used to compare the values obtained using Equation (6) with those obtained by means of simulation (using the finite element method and validating by means of hydraulic testing results). A summarized graphical result is represented in Figure 10.
Figure 10 shows that compared to Equation (6) results, submergence values simulated using the VOF method
![]()
Table 6. Polynomial adjustment parameter values for criti- cal submergence.
![]()
Figure 10. Critical submergence simulation quality obtained with Equation (6) in comparison to CFD simulation.
have an excellent accuracy index at 0.99498. It also reveals that this equation overestimates in 0.77 mm the number obtained using the VOF method, which means this type of estimation is always conservative in terms of safety.
Similarly, the effective submergence value was also adjusted. Data relating to the adjusting polynomial coefficients are those included in Table 7.
Figure 11 represents the comparison between values simulated using the two methods: finite element and polynomial.
Figure 11 shows that compared to zz equation results, effective submergence values simulated using the VOF method have an excellent accuracy index at 0.99513. It also reveals that this equation overestimates in 1.1 mm the number obtained using the VOF method, which means this type of estimation is always conservative in terms of safety.
4. Conclusions
This paper presents a method to estimate critical and effective submergence values using the numbers of Reynolds and Weber. The method allows for the introduction of fluid variables (surface tension, density, viscosity) in the calculation, which means effects relating to temperature and the type of fluid can be considered.
A specific equation for tanks with no fluid flow has been provided, and that is important because most formulations under analysis (Table 1) are specific for dam water intake systems and canals, and not so much for tanks.
The Hydraulic Institute formulation significantly overestimates the value of critical submergence for tanks in which the fluid is confined. This was clearly illustrated in the tests carried out in cases 9, 10 and 11 (Figure 12).
It is worth mentioning that the results obtained are also coherent with the outcome of the analysis published by the University of Stellenborg [7] .
![]()
Table 7. Polynomial adjustment parameter values for effective submergence.
![]()
Figure 11. Effective submergence simulation quality obtained with Equation (6) in comparison to CFD simulation.
![]()
Figure 12. Comparison between real values and simulated values (using the VOF, Equation (6) and HI methods).
Practically speaking, a conservative approach is taken to select the critical submergence value; having said that, the need for conservatism would have been more significant if the values of the Hydraulic Institute had been selected. Taking this critical submergence value without compromising generality or safety at any moment, results in a number of benefits, including an increase in the inventory of available fluid. This means that during the design phase, volume size can be reduced for a specific level of available volume.
As a result of all this, it is possible to conclude that the equation for estimating submergence, both critical and effective, based on the numbers of Reynolds and Weber, provides highly reliable, accurate numbers which are also in line with the finite element method simulation results. Thus, using the numbers of Weber and Reynolds as part of the proposed methodology, is a simple, highly efficient option to determine critical and effective submergence values.