The Geometrical Theory of the Structure of Nuclei, Atoms, and Molecules ()
1. Introduction
Democritus, the father of Greek Chemistry, was the originator of the atomic hypothesis. In 4C B.C. he came up with his atomic hypothesis that atoms are elementary indivisible and indestructible particles of which all matter was composed. The ideas of Democritus were expressed in the poem “De Rerum Natura” by Lucretius in the IC B.C.
There was, however, a rival hypothesis due to Aristotle which asserted that all matter was composed of varying proportion of the four Aristotelian elements, namely, earth, water, air, and fire. Because of the authority and overwhelming influence of Aristotle, the Democritian hypothesis was rejected, and the Aristotelian hypothesis was in force for about 2000 years.
Through the pioneering works of restless chemists of the 17, 18, and 19 centuries AD, notably Robert Boyle, Antoine Lavoisier, and John Dalton, the Aristotelian hypothesis was roundly condemned and eventually rejected. Their efforts, backed up by experimental results, helped to reinstate the Democritian hypothesis. Between 1860 and 1913 AD the empirical works of Chemists J.A.R. Newlands, D.I, Mendeleeve, H.G.J. Mosley and many others were summarized in a table called the Periodic Table of the Chemical Elements. The periodic table gave birth to the periodic law: The physical and chemical properties of the chemical elements vary periodically with the atomic number.
The periodic law implied that the atom, unlike the Democritian atom, had to be composite. The desire to determine what basic constituents of the atom could give rise to such a fundamental law brought physicists into the atomic fray. The fundamental experiments done between 1887 and 1932 by H. Hertz, A.H. Becquerel, Marie and Pierre Curie, E. Rutherford, J. Chadwick and many others brought about a new understanding of the structure and the nature of the forces in the atom. The atom consists of a central core called the nucleus surrounded by electrons, and the forces therein are non-Newtonian. By the 1920s classical field theory had made a remarkable transition to quantum field theory through the pioneering works of theorists M. Planck, L. de Broglie, W. Heisenberg, M. Born, P. Jordan, W. Pauli, E. Schrodinger, O. Klein, W. Gordon, P.A.M. Dirac, and others.
In 1926 Erwing Schrodinger took a giant step in the development of quantum mechanics with the construction of the Schrodinger equation which he applied to the Hydrogen atom. Schrodinger’s theory of the hydrogen atom recorded some spectacular results, but was flawed by the fact that it was a non-relativistic theory, amongst many other defects. In 1928 P.A.M. Dirac created his relativistic theory of the hydrogen atom called the Dirac equation [2] . Dirac’s theory is seminal in that it incorporated an internal degree of freedom called the spin of the electron and introduced antimatter into physics. Viewed from recent developments, Dirac’s theory was the first ever formal quantium physical theory in that it was constructed entirely in terms of 4-operators, namely,  ,
, 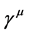 , and
, and .
.
As far as we know, no formal approach exists today for the treatment of many-electron atoms. The problem is so complex that only Schrodinger-based approximation methods have been developed: Variation calculations are used to obtain the ground states of the lightest atoms: for heavier atoms, the central-field approximation, Thomas-Fermi model, Hartree and Hartree-Fock approximations; and for nuclei, various many-body techniques are employed depending on the structure of the system. One major reason why these methods cannot yield satisfactory results is that, as palpably demonstrated by the Dirac’s theory, atoms are embedded in a 4-dimensional pseudoeuclidean background. Further, atoms, nuclei, and molecules are discrete systems, hence differential equations are not applicable. The Schrodinger theory is therefore not expected to apply to many-electron atoms! It is for this reason that we decide to consider other methods for the treatment of many-particle atoms and nuclear systems.
2. The Reducibility Scenario
The situation that confronts us in many-fermion systems is similar to the problem that gave birth to statistical mechanics at the beginning of the 20th century. Like that case a completely new approach is needed here.
Our solution is based on the reducibility theorem according to which a 4-quantum subspace of index  is reducible according to the fundamental formula [1] ,
is reducible according to the fundamental formula [1] ,
 (1)
(1)
The “2” outside the summation sign in (1) comes from the subspace of index  which is reducible to
which is reducible to ―the
―the 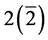 being the dimension of the subspace of index (rank)
being the dimension of the subspace of index (rank) . A 4-quantum space of index
. A 4-quantum space of index 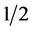 has no classical analogue―physically it is a 2―level cell occupied by fermions (“2”) and antifermions (“
has no classical analogue―physically it is a 2―level cell occupied by fermions (“2”) and antifermions (“ ”); the “2” gives the
”); the “2” gives the 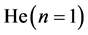 group, and “
group, and “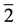 ” the antihelium group of chemical elements. Formula (1) is certainly true for atoms of the
” the antihelium group of chemical elements. Formula (1) is certainly true for atoms of the  etc. groups of chemical elements as we shall see.
etc. groups of chemical elements as we shall see.
3. The Periodic Table
The Formula (1) gives the structural design for all fermion systems in the universe. The structure can be interpreted by analogy with gravitation: Each term (period) gives the “floor” of a “building” in an electrostatic environment established by the nucleus and electrons. The first period (first term) is the “ground floor”, with antifermions (positrons and antineutrinos) forming the “foundation”; the second period (second term), “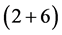 ”, is the “first floor/roof”, with the “2” serving as the “deck” separating the ground floor and the first floor; the third period (third term), “
”, is the “first floor/roof”, with the “2” serving as the “deck” separating the ground floor and the first floor; the third period (third term), “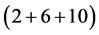 ”, gives the “second floor” with the “2” again serving as the “deck” separating the first floor and the second floor―the “10” cannot constitute another floor in this period because there is no provision for a deck separating it and the second floor, that floor will be built in the 4th period. The other periods are interpreted similarly. We shall now construct the periodic table of the chemical elements using the foregoing prescription and the dimensionality theorem. Here (X(a)) gives element “X” of atomic number
”, gives the “second floor” with the “2” again serving as the “deck” separating the first floor and the second floor―the “10” cannot constitute another floor in this period because there is no provision for a deck separating it and the second floor, that floor will be built in the 4th period. The other periods are interpreted similarly. We shall now construct the periodic table of the chemical elements using the foregoing prescription and the dimensionality theorem. Here (X(a)) gives element “X” of atomic number .
.
First period .
.
Geometrical structure: .
.
This is a “foundation” structure, the “ground floor” of the atomic world built with fermions and antifermions. For the electronic world the structure is (2), the s-shell having two levels, with the electronic configuration.
 .
.
State Kets:  where we have suppressed
where we have suppressed  from
from  from here on.
from here on.
Chemical elements:

Second period .
.
This is the first floor which has two levels (s-shell) as the deck and six levels (p-shell) as the first floor, with electronic configuration
 .
.
State Kets: .
.
Chemical elements:




Third period .
.
The admissible structure here is

with the 3d-shell outstanding, as explained before.
State Kets: 
Chemical elements:




4th period n = 4: .
.
Taking cognizance of the 3d-shell, the admissible structure is

with 4d and 4f shells outstanding because there is no provision for “decks” for them.
State Kets: 
Chemical elements:









5th period 
The procedure now has a familiar ring: The admissible structure is

 shells are outstanding there being no decks on which these floors would stand.
shells are outstanding there being no decks on which these floors would stand.
State Kets: 
Chemical elements:









6th period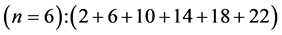 .
.
Given the deck “2” here “structural” stability requires that the 4f, 5d, and 6p shells constitute part of a floor on the 6s deck. Thus, the admissible structure is

with the  shells outstanding.
shells outstanding.
State Kets: 
Chemical elements:


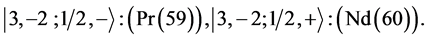




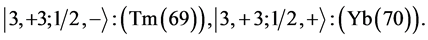








7th period 
The 7th period is similar to the 6th period.
The structure (electronic configuration) that improves stability is


State Kets: 
Chemical elements:
















This procedure can in principle be continued indefinitely so that one can construct any atom one desires; but the atomic structures become progressively unstable. Actual laboratory “construction” of these unstable atoms is possible but they have only a fleeting existence.
4. Conclusions
We infer from the foregoing that fermions reside in definite quantum states of definite angular momentum:  for the ground state and
for the ground state and  for all other states. Since
for all other states. Since  takes discrete values
takes discrete values , there are no fermion states for which
, there are no fermion states for which  This conclusion is in complete disagreement with conventional atomic and nuclear model (informal) theories. Further, because
This conclusion is in complete disagreement with conventional atomic and nuclear model (informal) theories. Further, because  takes all discrete values from
takes all discrete values from 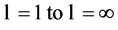 nature admits in principle infinite number of atoms. Finally, the labeling of atoms within each multiplex defined by
nature admits in principle infinite number of atoms. Finally, the labeling of atoms within each multiplex defined by  and s is arbitrary; here we have labeled the atoms consistently as follows:
and s is arbitrary; here we have labeled the atoms consistently as follows:

The fermion ground state, a pure quantum state, is described geometrically by  “2” for particle and “
“2” for particle and “ ” for antiparticle. The physical states, consistent with the dimensionality theorem, are
” for antiparticle. The physical states, consistent with the dimensionality theorem, are  for lepton ground state and
for lepton ground state and , for nucleon ground state. From these two states one builds atoms and antiatoms, consistent with the electrical neutrality of physical states [1] ,
, for nucleon ground state. From these two states one builds atoms and antiatoms, consistent with the electrical neutrality of physical states [1] ,  , which gives hydrogen and its two isotopes and helium and its two isotopes, and
, which gives hydrogen and its two isotopes and helium and its two isotopes, and 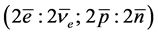 which gives antihydrogen and its two isotopes and antihelium and its two isotopes. We call the ground state
which gives antihydrogen and its two isotopes and antihelium and its two isotopes. We call the ground state  the helium group of chemical elements.
the helium group of chemical elements.
The so called first excited state  is the Neon group of chemical elements. Neutrinos are absent from this state and all other states
is the Neon group of chemical elements. Neutrinos are absent from this state and all other states 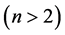 because on account of their very tiny mass they are not bound in these states [3] . There are a total of two electrons in the 2s-shell and six electrons in the 2p-shell. In the corresponding nucleus there are a total of 8 protons and 8 neutrons: 2 protons and 2 neutrons in the 2s-shell, and 6 protons and 6 neutrons in the 2p-shell. This gives a total of 8 chemical elements, and a number of isotopes. Other groups of chemical elements and the associated nuclei are treated similarly.
because on account of their very tiny mass they are not bound in these states [3] . There are a total of two electrons in the 2s-shell and six electrons in the 2p-shell. In the corresponding nucleus there are a total of 8 protons and 8 neutrons: 2 protons and 2 neutrons in the 2s-shell, and 6 protons and 6 neutrons in the 2p-shell. This gives a total of 8 chemical elements, and a number of isotopes. Other groups of chemical elements and the associated nuclei are treated similarly.
The electronic states of molecules are more complex than the atomic and nuclear states. These states can, however, be deduced from the electronic states of atoms. As an example we consider Hz-molecule. The state ket of H2 is just the tensor product of state kets of two hydrogen atoms  The term “bond” used by chemists has no physical meaning etc.
The term “bond” used by chemists has no physical meaning etc.
Our theoretically derived periodic table (PT) confirms and generalizes the conventional PT of the chemical elements. The horizontal rows of elements are called periods, numbered from  instead of from 1 to 7. The first period has a total of 8 levels corresponding to 2 elements, 2 antielements, 2 neutrinos, and 2 antineutrinos, whereas the conventional PT has just 2 levels corresponding to just 2 elements. The second and third periods each has 8 levels (8 elements); the fourth and fifth periods each has 18 levels (18 elements); and the sixth and seventh periods each has 32 levels (32 elements), etc. The period, defined as the number of levels of a particular period, irrespective of the number of levels belonging to other earlier periods appearing in that period, is 8. This is in complete agreement with the dimensionality law.
instead of from 1 to 7. The first period has a total of 8 levels corresponding to 2 elements, 2 antielements, 2 neutrinos, and 2 antineutrinos, whereas the conventional PT has just 2 levels corresponding to just 2 elements. The second and third periods each has 8 levels (8 elements); the fourth and fifth periods each has 18 levels (18 elements); and the sixth and seventh periods each has 32 levels (32 elements), etc. The period, defined as the number of levels of a particular period, irrespective of the number of levels belonging to other earlier periods appearing in that period, is 8. This is in complete agreement with the dimensionality law.
The vertical columns define families of elements: The first 2 columns correspond to elements of angular momentum (spin) , the last 6 columns correspond to elements of angular momentum
, the last 6 columns correspond to elements of angular momentum , and the 10 columns lying between the first 2 and the last 6 columns correspond to elements of angular momentum
, and the 10 columns lying between the first 2 and the last 6 columns correspond to elements of angular momentum 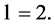 Further the 14 columns of the Rare Earths (Lanthanide Series) and Actinide Series correspond to elements of angular momentum
Further the 14 columns of the Rare Earths (Lanthanide Series) and Actinide Series correspond to elements of angular momentum  etc. Thus, the index n of the quantum space (principal quantum number, period) enumerates the groups of chemical elements and angular momentum
etc. Thus, the index n of the quantum space (principal quantum number, period) enumerates the groups of chemical elements and angular momentum enumerates the families of chemical elements.
enumerates the families of chemical elements.
Lastly, we call the world constructed with leptons and nucleons matter world. A world analogous with the matter world, called antimatter world, can be constructed in a similar way with antileptons and antinucleons. Thus, there exists matter―antimatter symmetry in the fermion world.