Application of Classification of Traveling Wave Solutions to the Zakhrov-Kuznetsov-Benjamin-Bona-Mahony Equation ()
1. Introduction
The nonlinear partial differential equation (PDE) is widely used to describe physical phenomena in various fields of sciences, especially in fluid mechanics, solid state physics, plasma physics, plasma waves, biology and so on. During the past few decades, various methods have been developed by researchers to find the solutions for the NLEEs.
In this article, we will use complete discrimination system for polynomial proposed by Liu [1] -[4] to study the traveling wave solutions of the ZK-BBM equation. The generalised form of the (2 + 1) dimensional ZK-BBM equation is given as:
 (1)
(1)
where  and
and  are arbitrary constants.
are arbitrary constants.
Equation (1) arises as a description of gravity water waves in the long-wave regime [5] [6] . The solutions of Equation (1) have been studied in various aspects. For example, Sadaf Bibi [7] used the Sine-cosine method to obtain the travelling wave solutions of Equation (1). Rajesh Kumar Gupta [8] used the  -expansion method to find some hyperbolic, trigonometric and rational solutions, and so on. It is worth mentioning that Wazwaz [9] [10] made a detailed study for compact and noncompact physical structures and calculated the exact solutions of compact and noncompact structures by the extended tanh method for the ZK-BBM equation.
-expansion method to find some hyperbolic, trigonometric and rational solutions, and so on. It is worth mentioning that Wazwaz [9] [10] made a detailed study for compact and noncompact physical structures and calculated the exact solutions of compact and noncompact structures by the extended tanh method for the ZK-BBM equation.
2. Classification
Taking the traveling wave transformation  and
and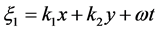 , we can obtain the corresponding reduced ODE of Equation (1).
, we can obtain the corresponding reduced ODE of Equation (1).
 (2)
(2)
Integrating Equation (2) with respect to  once, we yield
once, we yield
 (3)
(3)
where  is an integral constant.
is an integral constant.
Equation (3) can be written as
 (4)
(4)
where .
.
From Equation (4) we have
 (5)
(5)
where  is an integral constant.
is an integral constant.
We use the complete discrimination system for the third order polynomial and have the following solving process.
Let
 (6)
(6)
Then Equation (5) becomes
 (7)
(7)
where  is a function of
is a function of . The integral form of Equation (7) is
. The integral form of Equation (7) is
 (8)
(8)
Denote
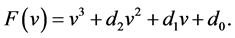 (9)
(9)
 (10)
(10)
According to the complete discrimination system, we give the corresponding single traveling wave solutions to Equation (1).
Case 1.  has a double real root and a simple real root. Then we have
has a double real root and a simple real root. Then we have
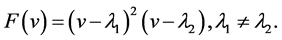 (11)
(11)
when , the corresponding solutions are
, the corresponding solutions are
 (12)
(12)
 (13)
(13)
 (14)
(14)
Case 2.  has a triple root. Then we have
has a triple root. Then we have
 (15)
(15)
The corresponding solution is
 (16)
(16)
Case 3.  has three different real roots. Then we have
has three different real roots. Then we have
 (17)
(17)
when , we take the transformation as follows
, we take the transformation as follows
 (18)
(18)
According to the Equation (8), we have
 (19)
(19)
where .
.
On the basis of Equation (19) and the definition of the Jacobi elliptic sine function, we have
 (20)
(20)
The corresponding solution is
 (21)
(21)
when  we take the transformation as follows
we take the transformation as follows
 (22)
(22)
The corresponding solutions is
 (23)
(23)
where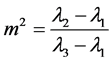 .
.
Case 4.  has only a real root. Then we have
has only a real root. Then we have
 (24)
(24)
when , we take the transformation as follows
, we take the transformation as follows
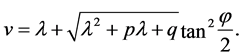 (25)
(25)
According to the Equation (8), we have
 (26)
(26)
where .
.
On the basis of Equation (26) and the definition of the Jacobi elliptic cosine function, we have
 (27)
(27)
The corresponding solutions is
 (28)
(28)
In Equations (12), (13), (14), (16), (21), (23) and (28), the integration constant 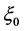 has been rewritten, but we still use it. The solutions
has been rewritten, but we still use it. The solutions  are all possible exact traveling wave solutions to Equation (1). We can see it is easy to write the corresponding solutions to the ZK-BBM equation.
are all possible exact traveling wave solutions to Equation (1). We can see it is easy to write the corresponding solutions to the ZK-BBM equation.
3. Conclusion
In this article, the traveling wave solutions to ZK-BBM equation were obtained by the complete discrimination system for polynomial and direct integral method. This method has the characteristics of simple steps and clear effectivity. In this way we can solve a lot of other equations.
Acknowledgements
I would like to thank the referees for their valuable suggestions.