A Simple Way to Prove the Characterization of Differentiable Quasiconvex Functions ()
1. Introduction
Quasiconvex functions play an important role in several branches of applied mathematics (e.g. mathematical programming, minimax theory, games theory, etc.) and of economic analysis (production theory, utility theory, etc.). De Finetti [1] was one of the first mathematicians to define quasiconvex functions as those functions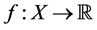
, 
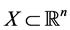being a convex set, having convex lower level sets, i.e. the set
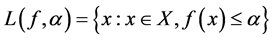
is convex for every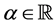
.
De Finetti did not name this class of functions: the term “quasiconvex (quasiconcave) function” was given subsequently by Fenchel [2] . It is well-known that the above characterization is equivalent to
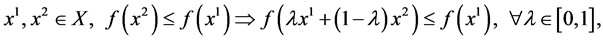
i.e., in a more symmetric way,
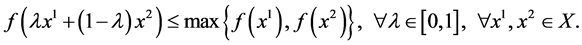
When f is differentiable on the open convex set 
we have the following characterization of a quasiconvex function.
Theorem 1. Let 
be differentiable on the open convex set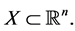 
Then f is quasiconvex on X if and only if
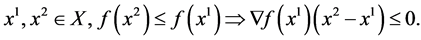(1)
Theorem 1 was given by Arrow and Enthoven [3] ; however, these authors prove, in a short and easy way, only the necessary part of the theorem, but not the converse property, whose proof is indeed presented in a quite intricate way by several authors (see, e.g. [4] -[11] ). Here we present an easy proof of Theorem 1, by exploiting some results on quasiconvexity of functions of one variable, results therefore suitable for geometrical illustrations. We need two lemmas.
Lemma 1. Let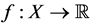
, 
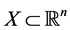a convex set. Then f is quasiconvex on X if and only if the restriction of f on each line segment contained in X is a quasiconvex function, i.e. if and only if the function 
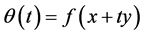is quasiconvex on the interval
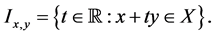
Proof. The quasiconvexity of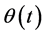 
is equivalent to the implication
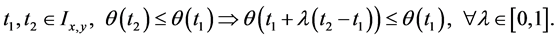
By setting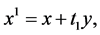 
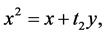we have 
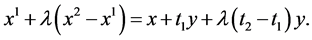The thesis follows by noting that 
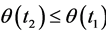and the logical implication
, 
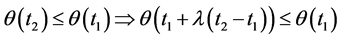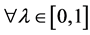are equivalent to 
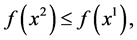and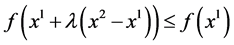
, 
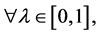respectively. 
The next lemma is proved in Cambini and Martein [12] and is given also by Crouzeix [13] , without proof.
Lemma 2. Let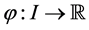 
be differentiable on the interval
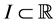; then 
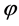is quasiconvex on I if and only if
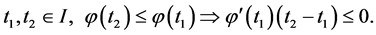(2)
Proof. Let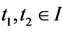 
such that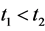 
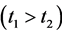and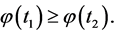 
The quasiconvexity of 
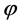implies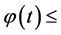 
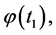
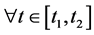
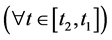so that 
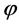is locally non-increasing (locally non-decreasing) at t1 and consequently (2) holds. Assume now that (2) holds. If 
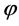is not quasiconvex, there exist 
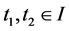with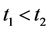 
such tha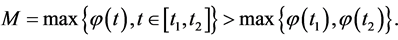t 
Let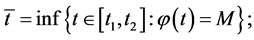 
the continuity of
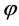implies the existence of 
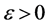such that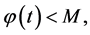 
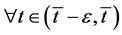and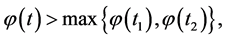 
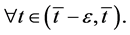The mean value theorem applied to the interval 
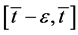implies the existence of
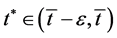such that 
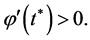Consequently, we have 
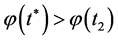with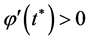 
and this contradicts (2). 
Proof of Theorem 1.
It is sufficient to note that if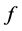 
is differentiable on the open and convex set 
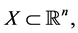then we have, with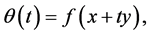 
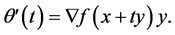
Therefore, on the ground of Lemmas 1 and 2, if we put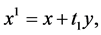 
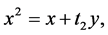we have 
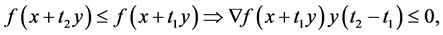i.e. 
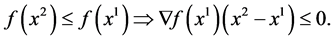
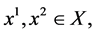
Finally, we point out that the proof of Ponstein [10] can be shortened as follows:
1) Let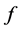 
be quasiconvex (and differentiable) on the open and convex set 
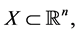i.e. let
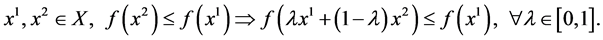
By the mean value theorem there exists a number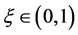 
such that
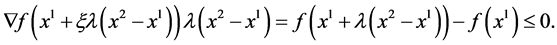
Dividing by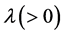 
and letting 
we have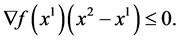 
2) Assume conversely that (1) holds and that for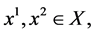 
with 
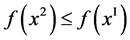there exists a point 
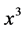between 
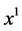and 
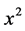with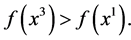 
Then there exists near 
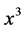(e.g. between 
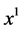and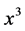
) also a point 
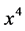with 
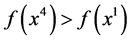and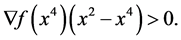 
Indeed, if for all x between 
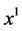and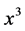 
it would hold 
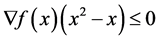or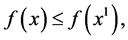 
then we would have 
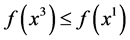but not 
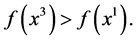But, being
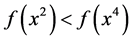, this implies
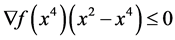, in contradiction with the inequality previously obtained. 