1. Introduction
There are many observations to suggest that neutrinos may be superluminal particles although OPERA has claimed an error for measuring the speed of neutrinos. [1,2]. In recent years, many convincing evidences for neutrino oscillation come from the solar and atmospheric neutrino data have shown that neutrinos have tiny mass (about 1 eV) or mass-square difference [3-6].
It was recorded from SN 1987A that 24 neutrinos observed in the Kamioka and Baksan detectors arrived about 3 hours before the light. This early arrival was presumably due to the delay experienced by photons emitted from the collapsing SN core, which was not the case for the emitted neutrinos. However, the value of the photon delay does not need the entire 3 hours, therefore the early neutrino arrival is normally assumed to set only an upper limit on any excess above c for their speed, the ratio < 2 × 10−9. One cannot rule out neutrinos as superluminal particles [7-11].
Parity violation is a specific feature of the weak interaction. It was first argued by T.D. Lee and C.N. Yang in 1956 [12] and experimentally established by C.S. Wu in beta-transition of polarized Cobalt nuclei [13]. In the standard model, neutrinos have naturally zero mass. Three flavors of neutrinos are purely left-handed, but anti-neutrinos are right-handed. If the neutrino has a tiny rest mass, it would move slower than light. When taking a Lorentz boost with a speed faster than the neutrino, the helicity of the neutrino would change its sign in the new reference frame. In another word, parity would not be violated in the weak interactions.
In order to solve this dilemma, the hypothesis that neutrinos may be superluminal particles is further investigated in this paper. To keep causality for superluminal particles, a kinematic time under a non-standard form of the Lorentz transformation is introduced, which is related to a preferred frame.
2. Negative Mass-Square of Neutrino
The square of the neutrino mass is measured in tritium beta decay experiments by fitting the shape of the beta spectrum near endpoint. In many experiments, it has been found to be negative.
The masssquare of the electron neutrino, m2(ne), is measured in tritium beta decay experiments (3H ® 3He + e + ne). In most recent experiments, the results have shown negative values. These data are listed in “Review of Particle Physics 2010”, and the average value of m2(ne) = -1.1 ± 2.4 eV2. The corresponding document sources can be also found in [14].
The negative value of the electron neutrino masssquare measurement simply means:
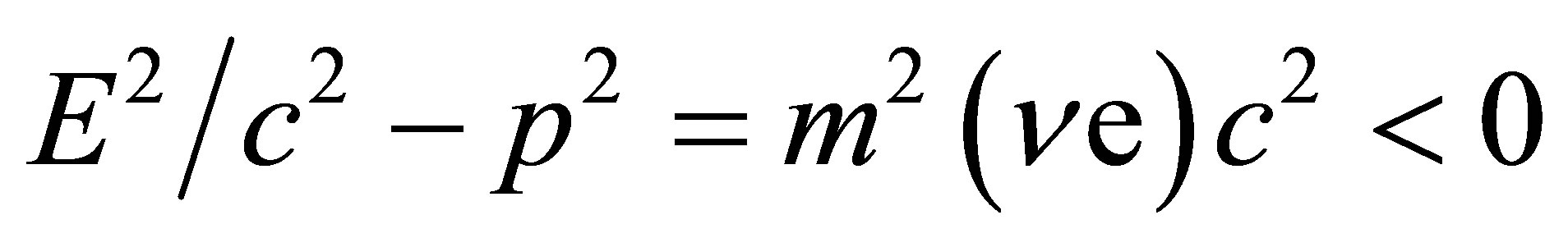(1)
These results strongly suggest that electron neutrinos might be tachyons, namely, particles that are faster than light. Furthermore, not only electron neutrinos have negative value of mass-square, but also muon neutrinos. From the pion decay experiment (p+ ® m+ + nm) [14], the recent measurement of the muon neutrino masssquare is m2(nm) = -0.016 ± 0.024 MeV2.
Besides neutrino oscillations, the cosmic ray spectrum at E ≈ 1 − 4 PeV [15,16] has suggested that the electron neutrino is a tachyon. Using a model to fit data, it yields a value for m2(νe) ≈ −3 eV2, which is consistent with the results from the measurements in tritium beta decay experiments.
In an early paper [17,18], the neutrinos is suggested to be a candidate as superluminal particles. The reasons are as follows:
1) Neutrinos have peculiar properties which are quite different from all other particles. They are electrically neutral, and only have weak interactions with other particles.
2) The proper mass of a neutrino is very close to zero. As we know, there are two kinds of neutrinos at least: νe and νμ (now we know one more type, ντ). Although they have very similar properties, they certainly are different particles. On the other hand, photons with many different frequencies are still considered as one kind of particle because they have zero mass. From the viewpoint of the existing tachyons, the answer is simple: νe and νμ do have different non-zero mass, thus they are two kinds of particles. In this way, we can give a natural explanation why the numbers of e-lepton and μ–lepton are conservative, respectively.
3) In order to explain the famous experiment of parity non-conservation, the two-component neutrino theory has been introduced. The positive neutrino is given a left-hand spin and the negative a right-hand spin. It means the speed of an observer in any frame must be less than the speed of neutrino, otherwise the direction of the neutrino’s spin will be changed. In other words, the neutrino must be a particle with the speed of light or faster than light.
3. Three Classes of Particle
Based on SR, superluminal particles were proposed by Bilaniuk et al. [17] as well as Feinberg and Recami et al. [18,19]. The sign of 4-D line element, ds2, is associated with three classes of particles. For simplicity, let dy = dz = 0, then Class I (conventional particles)
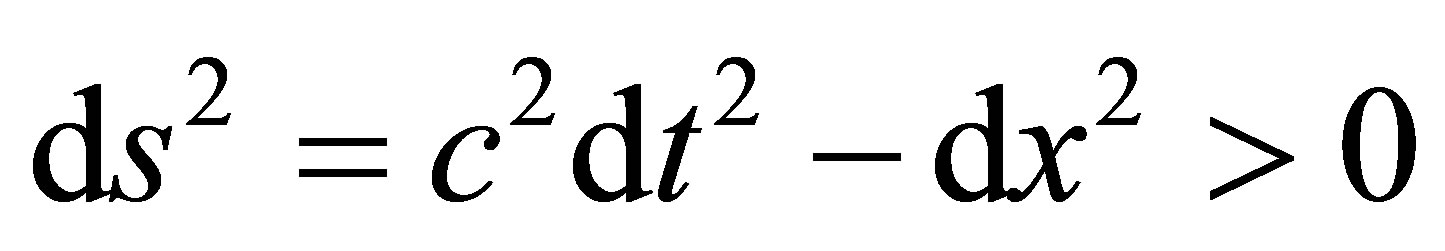
Class II (photon)
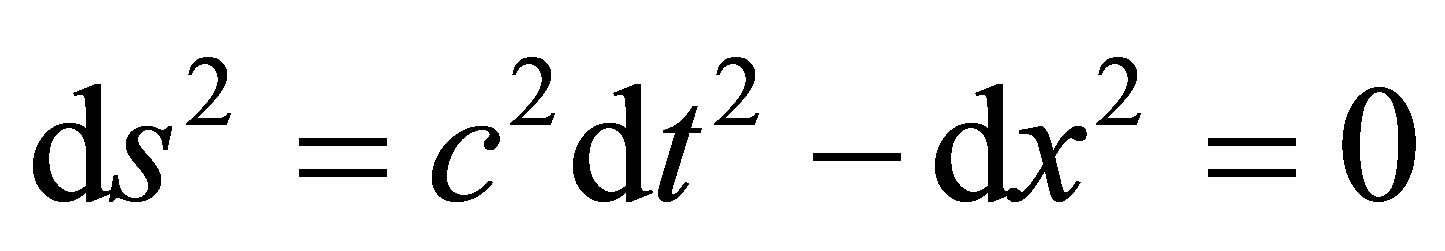(2)
Class III (tachyon) ds2 < 0 According to SR, all of particles with a rest mass mo (Class I) cannot travel faster than light. For Class I particle, the relation of energy and momentum in any inertial frame is as follows:
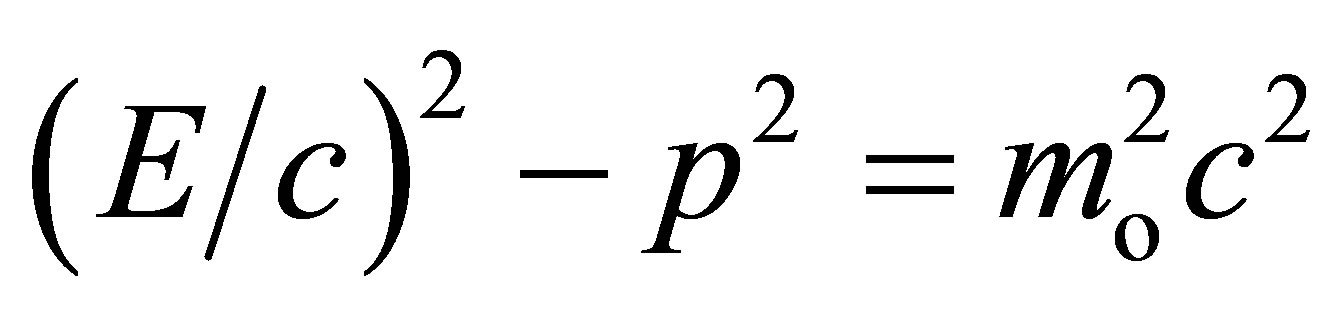(3)
The photon is a Class II particle: a quantum particle of light. Whatever energy a photon has, it always travels with the speed of light in vacuum. People usually consider the photon to have zero rest mass. In fact, “rest mass” is not a good term for a photon because there is no such reference frame that a photon becomes a stationary particle. As a good term, we may say that a photon has zero mass.
As far as Class III particles, that is superluminal particles or simply tachyons, the relation of momentum and energy is shown in Equation (1). Notice the minus sign on the right hand side of Equation (1) for superluminal particles. It means that a superluminal particle has a non-zero proper mass, and p2 is always greater than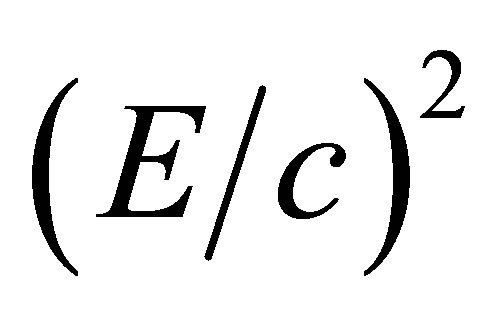
. Because the speed of a superluminal particle, us, is always greater than the speed of light, the momentum and energy in terms of us are as follows:
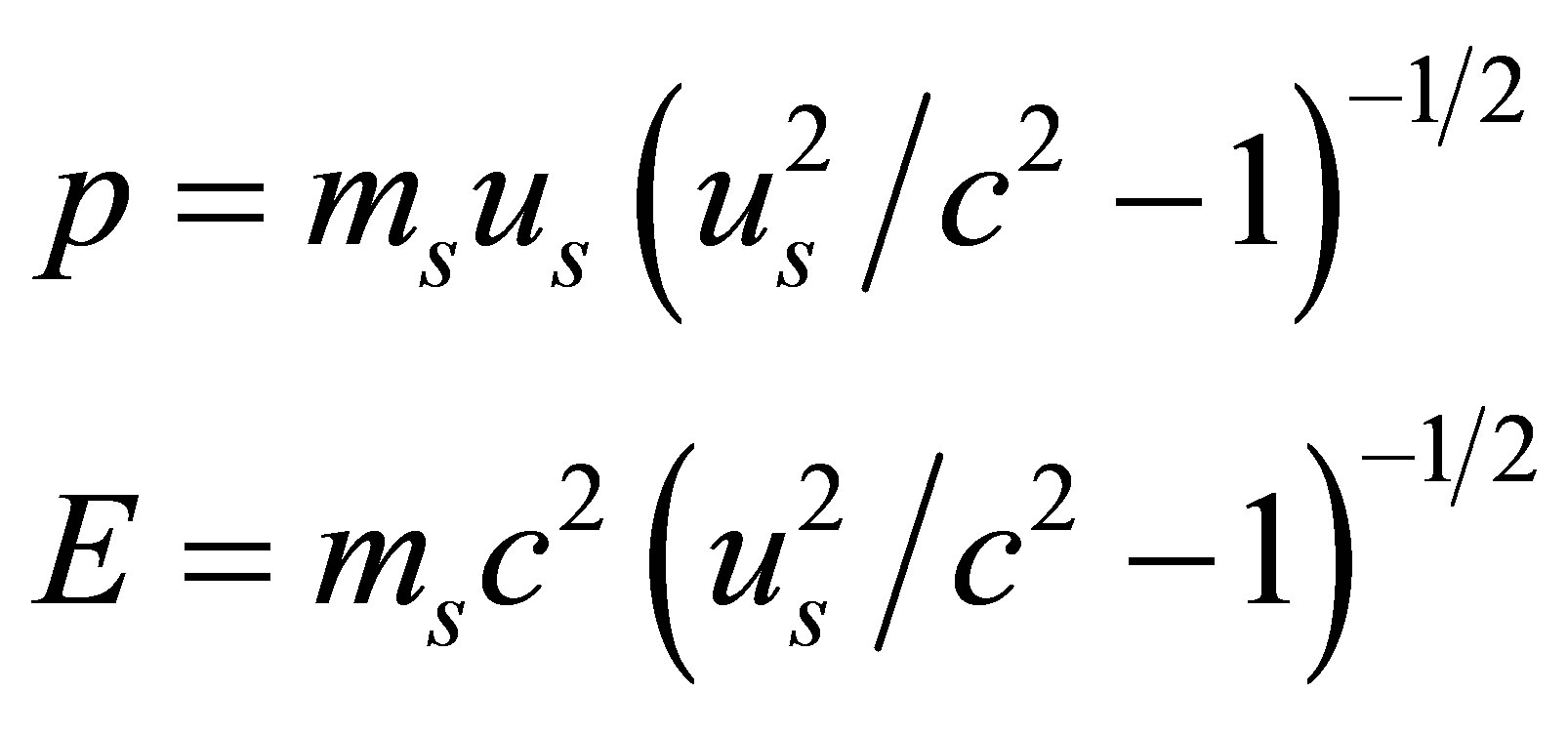(4)
where ms is the non-zero proper mass. From Equation (4), it is easily seen that when us is increased, p and E would be decreased. This property is opposite to that of a Class I particle. An illustration of energy vs. velocity for three classes of particles is shown in Figure 1.
Because any physical reference system is built by Class I particles (atoms, molecules etc.), it is assumed that any reference frame moves with a speed slower than light. On the other hand, once a tachyon is created in an interaction, its speed is always greater than the speed of light. The main problem in introducing a tachyon existing in SR is as follows: Suppose that a tachyon is seen by an observer. Then under the Lorentz transformation, another moving observer might see this tachyon to travel
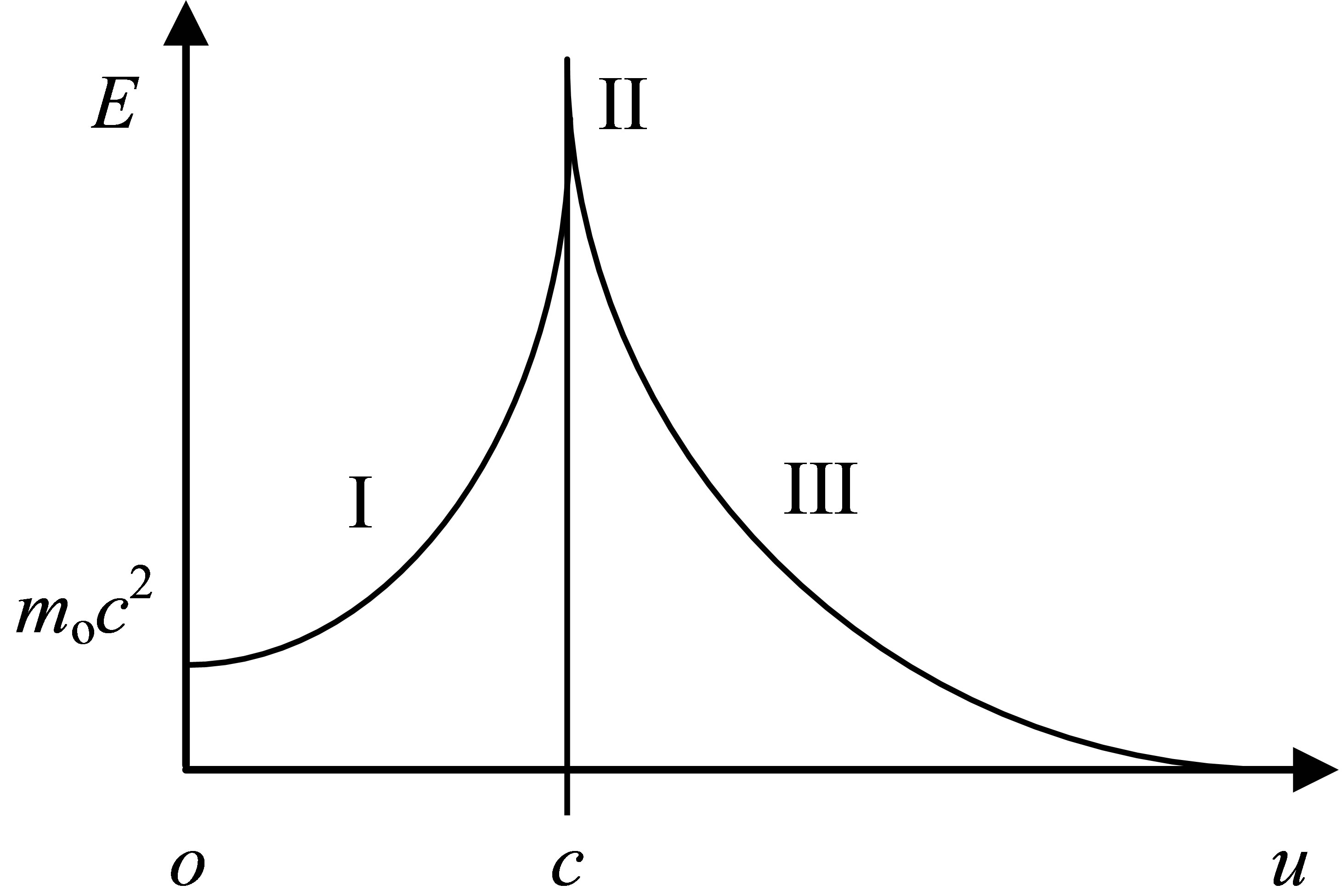
Figure 1. Energy vs. velocity for three classes of particles.
backward in time. To keep causality for superluminal particles, a non-standard form of the Lorentz transformation has been studied, which is called the generalized Galilean transformation (GGT).
4. GGT and a Preferred Frame
Within the context of the variation principle, it is well known that there is the freedom to choose different types of physical time [21,22]. The invariant four-line element can be written in arbitrary coordinates.
In general, the invariant four-line element can be written in arbitrary coordinates
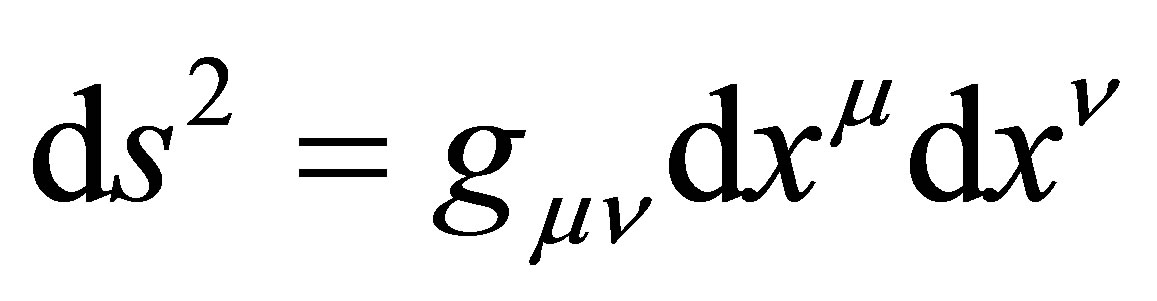(5)
where index m (or n) = 0,1,2,3. The 0th coordinate is called the time coordinate, which is related to the measured time, but is usually not identical to it. The action integral for a free particle has a form:
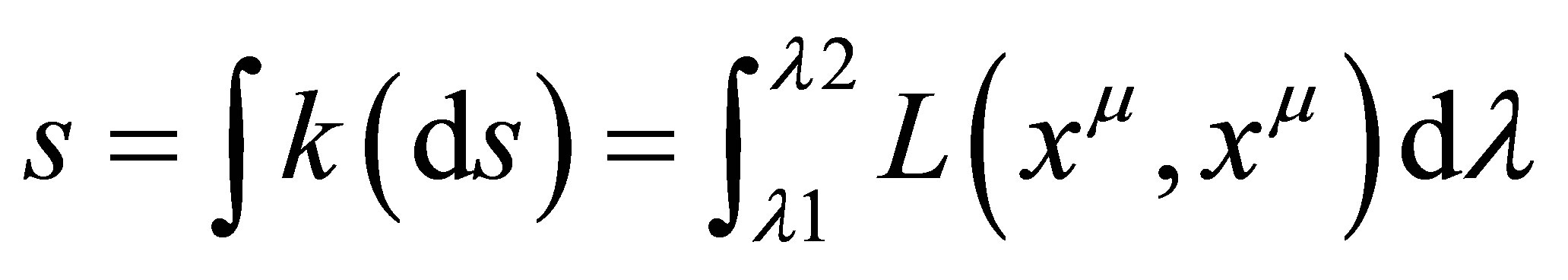(6)
where the constant k = mc, xm =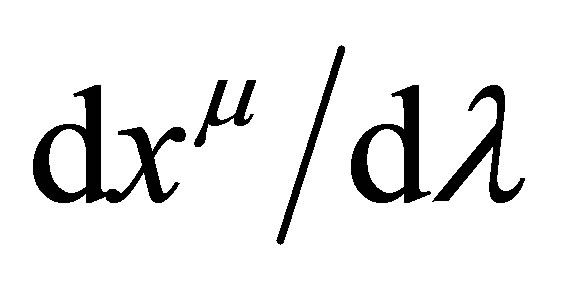 
and l is called the evolution parameter, which also plays roll of time. 
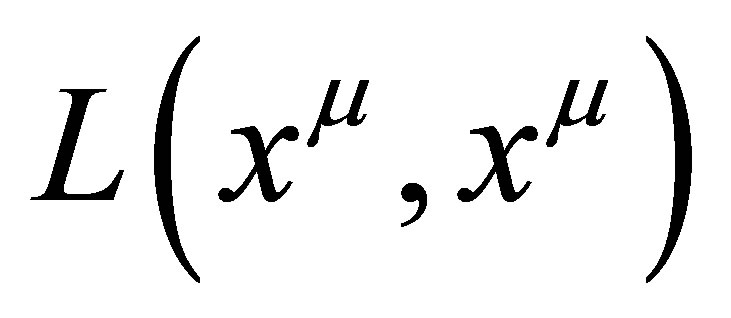is the Lagrangian in four-dimensional space,
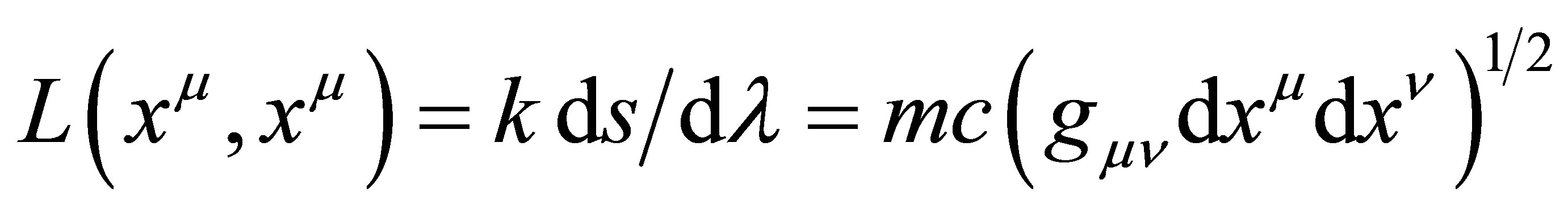(7)
Using the Eular-Lagrange equation in terms of the variation principle, we can obtain the geodesic equations:
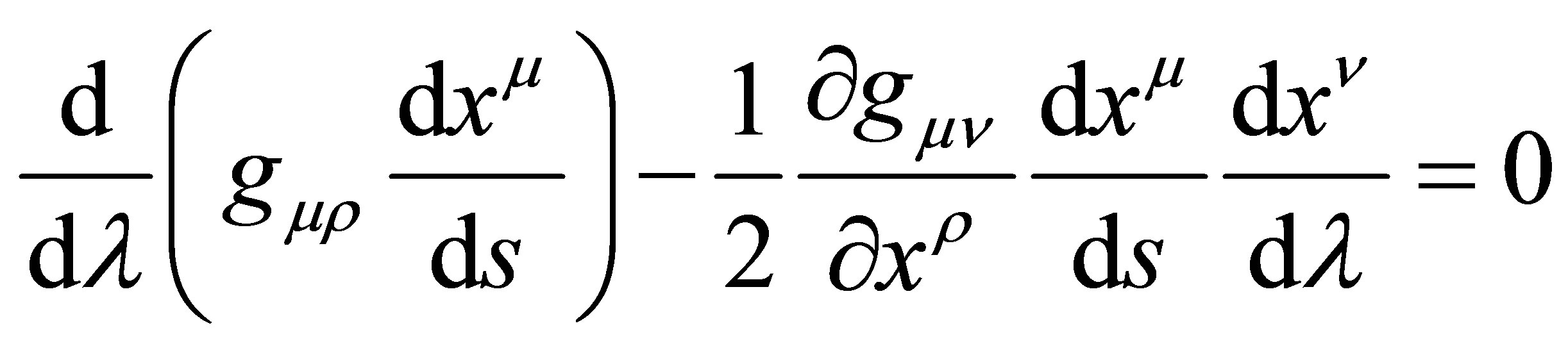(8)
This equation is valid for any choice of the evolution parameter l. The above method can be applied to the space-time theories in flat space although it is frequently used in general relativity. Furthermore, when we consider a specific evolution parameter as the physical time in all of the inertial frames, certain consistent rule must be imposed. Under this constraint, the definitions of physical time are not arbitrary, but there are only a few choices.
Besides the definition of relativistic time, another natural time defined by a generalized Galilean transformation (GGT) has been studied [23-26]. It has been shown that GGT is a non-standard form of the Lorentz transformation (LT). It means that GGT and LT are equivalent if we describe particles with speed less than (or equal to) light. On the other hand, when describing superluminal particles, GGT is better than LT.
Let us start with a simplified 4-D line element, ds2 = c2dT2 − dX2, in a preferred inertial frame S(X, T). Consider another inertial frame, S(x ,t), which moves with a constant velocity v < c along x axis respect to S. The 2-D form of GGT can be written in
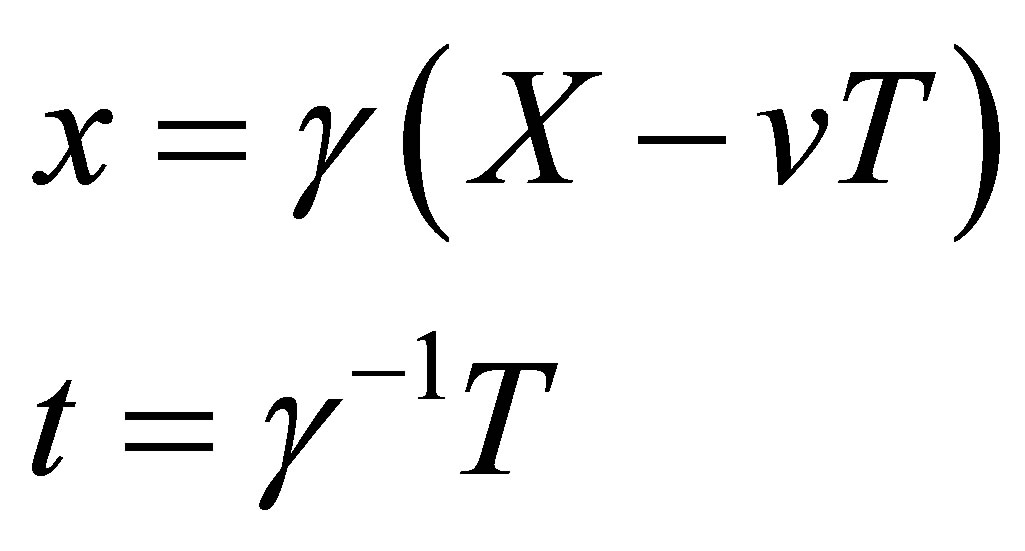(9)
where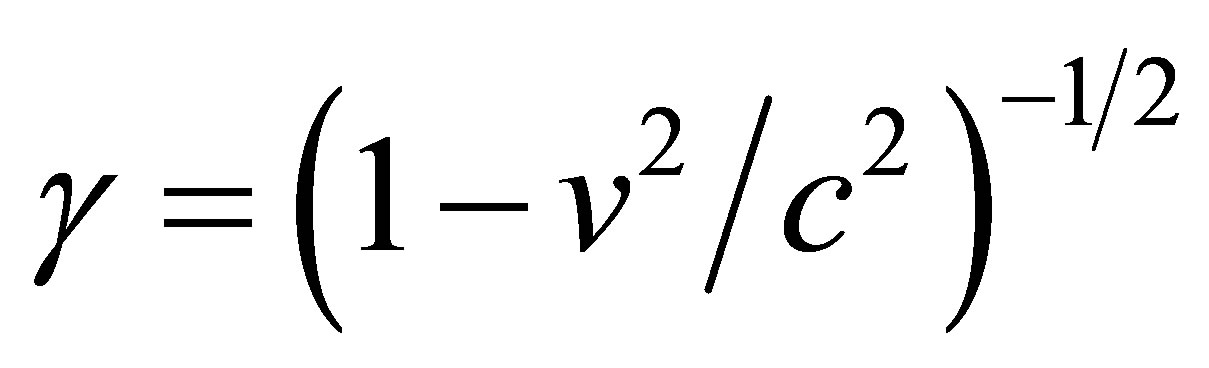 
is the factor of time dilation or length contraction. It is easily seen from Equation (9) that the synchronization of distant events is absolute, independent of the choice of the reference frame. A simplified 2-D illustration of GGT is shown in Figure 2. Therefore, GGT represents a non-rectangular transformation.
From the second equation of GGT in Equation (9), the time arrow is always positive in any reference frame. This property can also be seen in Figure 2: both of TA and tA are positive for a tachyon. The problem of backward time travel does not happen here. Since the synchronization is absolute under GGT, causality holds for all three types of particles including tachyons.
If the first equation of GGT is divided by the second equation in Equation (9), then we get the velocity transformation in x direction. It is
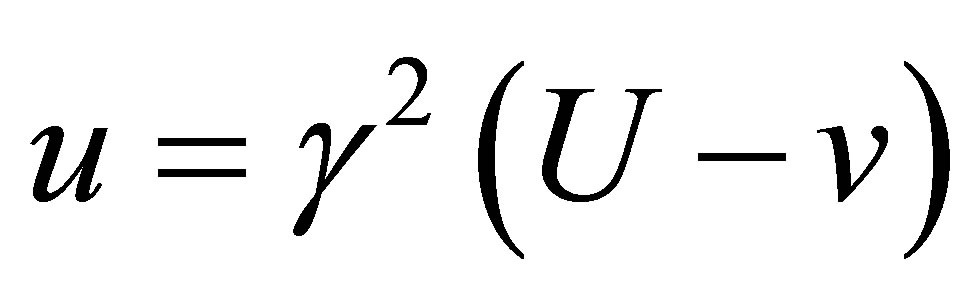(10)
where u =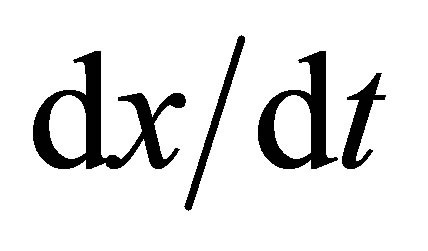
, and U =
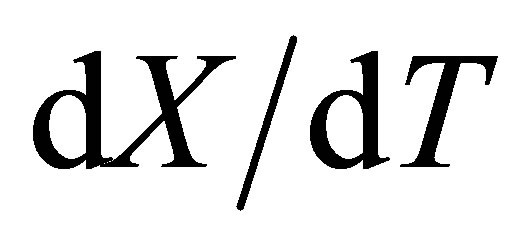. For example, the speed of light in the Frame S is a constant U = c, then the speed of light in a frame S along the x direction is
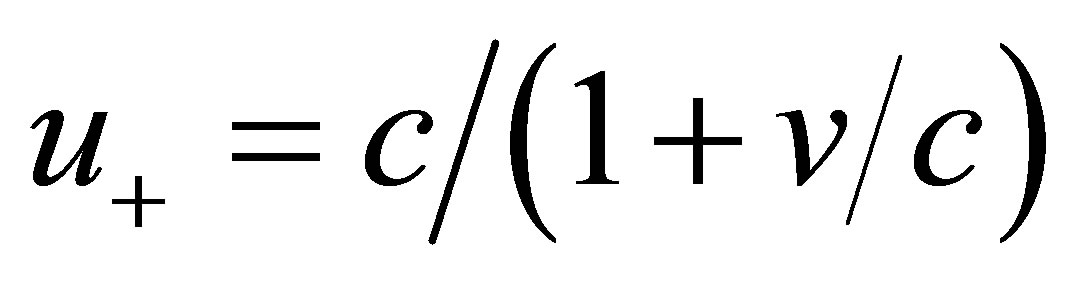. On the other hand, when the light moves along the −x direction, then
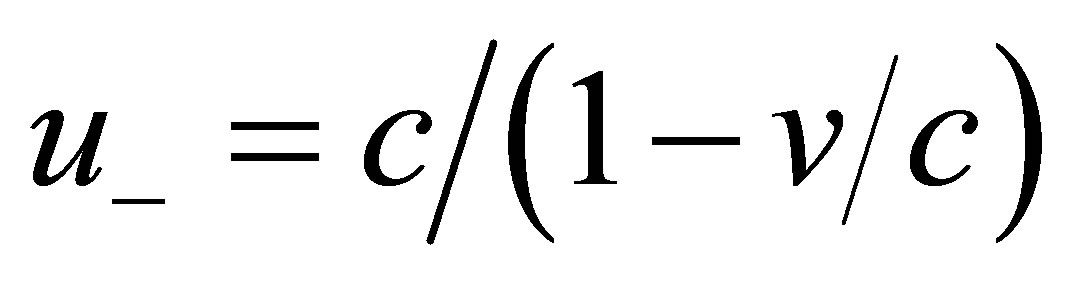. It means that the speed of light is directiondependent. Using these two expressions, the famous MichesonMorley (M-M) experiment can easily be explained. In fact, the light travels forth and back in M-M experiment. Let the lightpath in the frame S along the x direction be L, then the total travel time is
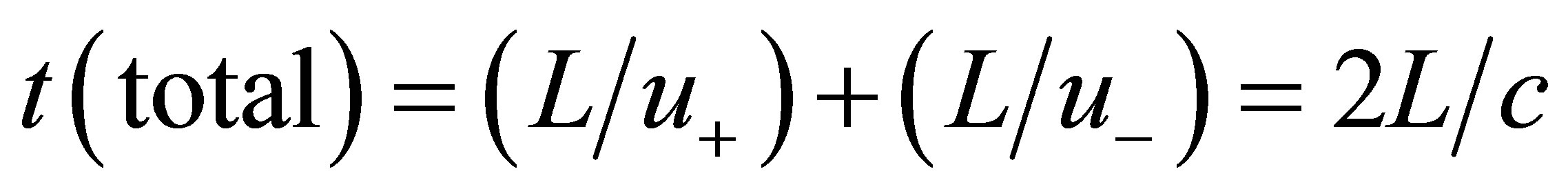(11)
Therefore, the total travel time is a constant for a round trip. It has been shown that the v is always cancelled out and GGT is equivalent to SR in known optical experiments [27].
The formulation of energy and momentum under GGT In terms of GGT, 4-D line element can be written in a more general form.
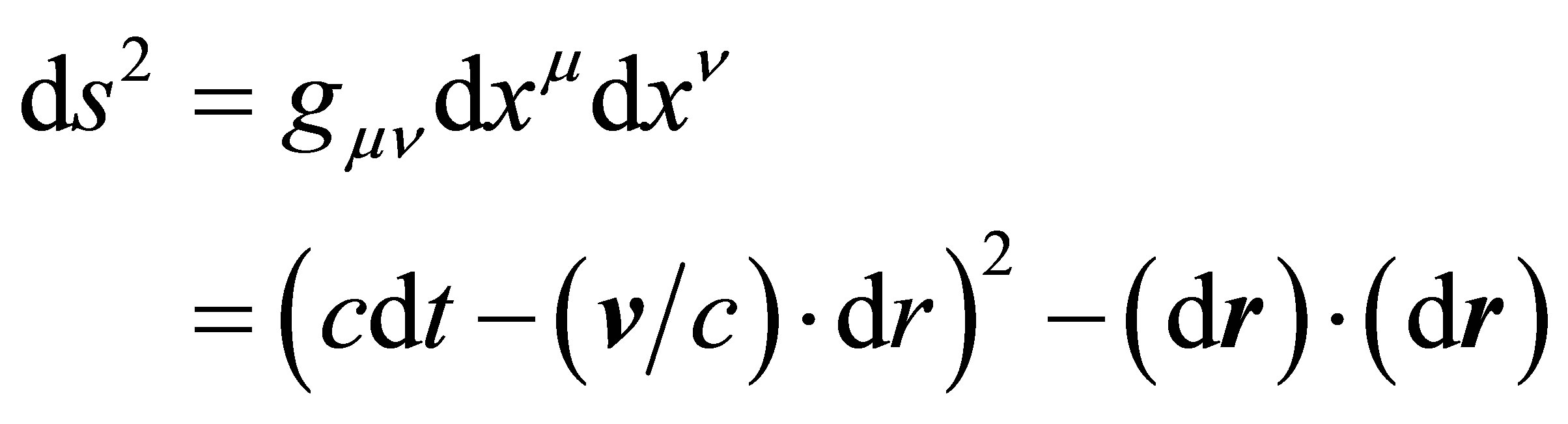(12)
For Class I particles, its 4-D momentum can be defined as
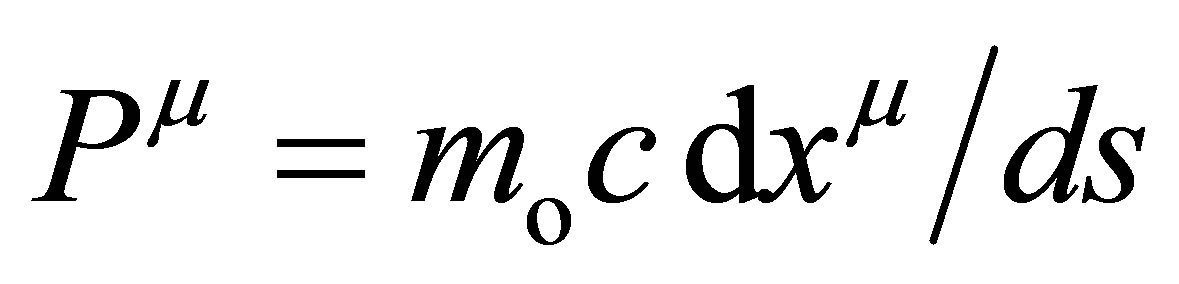(13)
where the contravariant 4-D momentum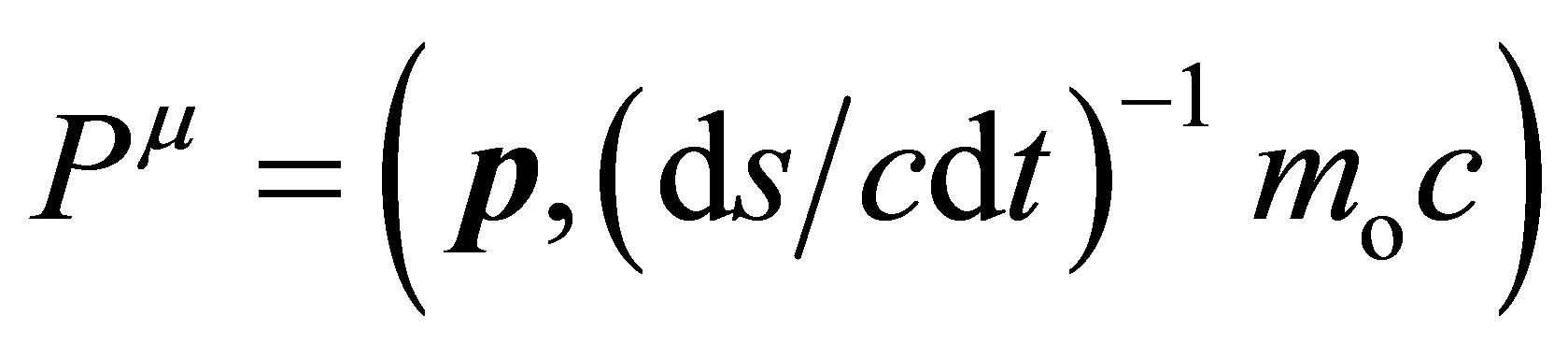 
. Using tensor calculus, the covariant 4-D momentum can be obtained as Pm = gmnPn. It can be easily proven that the relation of energy and momentum under GGT can be expressed as Equation (3), which is the same as from SR.
For Class III particles, since ds2 < 0, we need to introduce an invariant,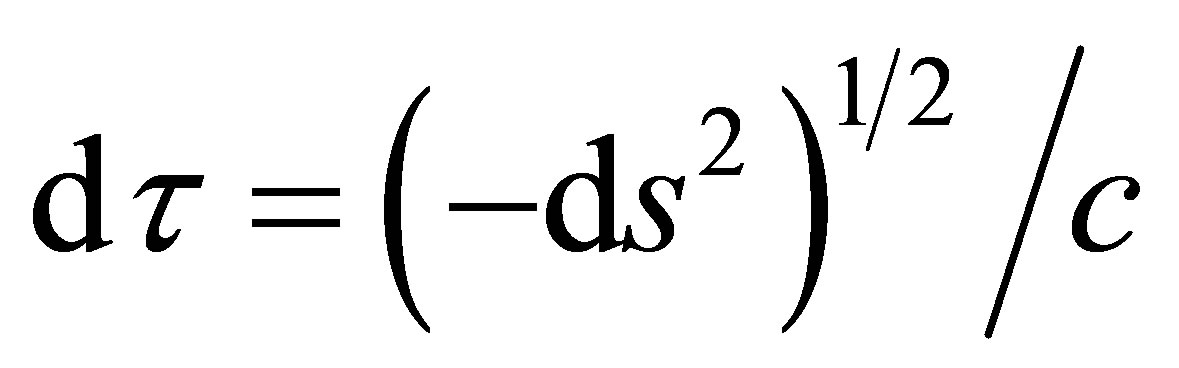 
, then the contravariant 4-D momentum for a tachyon can be defined as
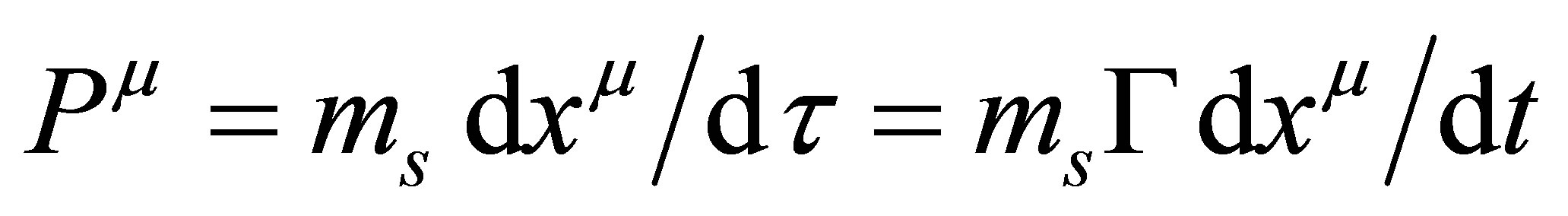(14)
where ms is the proper mass, and the coefficient
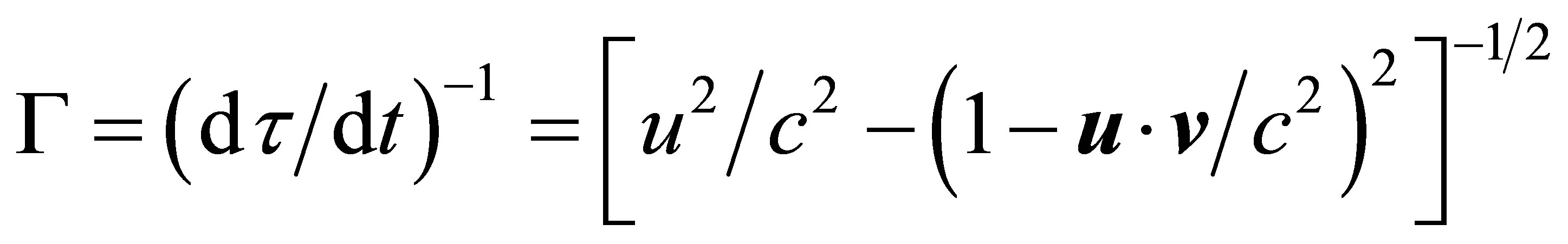(15)
Then the 3-D momentum of a tachyon becomes
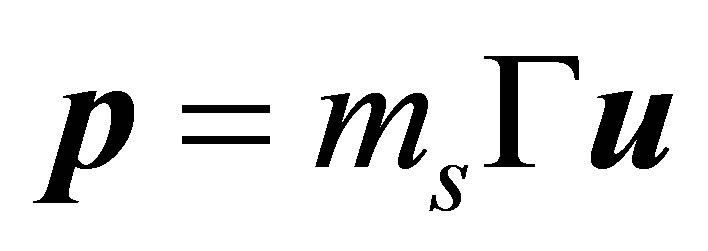(16)
and the energy
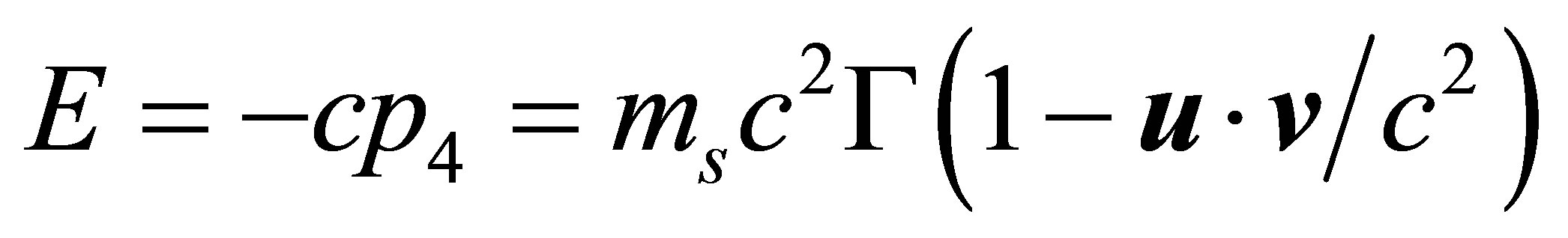(17)
Only in the preferred inertial frame S, Equations (16) and (17) are reduced to Equation (3). We assume that a tachyon has only a positive energy in S. From the above two equations, it is easily seen that when u is increased, p and E would be decreased. Furthermore, it can be proven that for tachyons we have
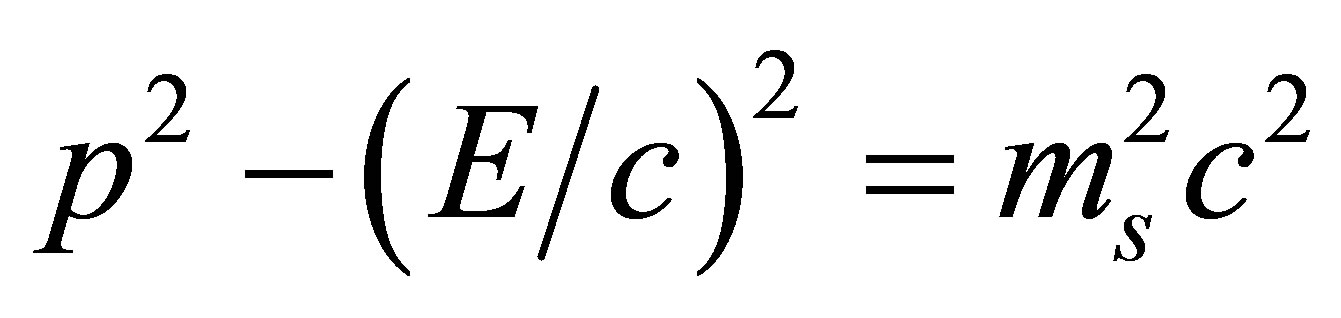(18)
Equation (18) is valid in any inertial frame. Thus the property of invariance for three classes of particles are preserved under the GGT framework.
Notice that from Equations (16) and (17), the two curves for a tachyon are not symmetric. This is because in a non-preferred reference frame, the lower limit values of momentum and energy for tachyons are different. This can be derived from Equations (16) and (17) when velocity u ® ¥. They become
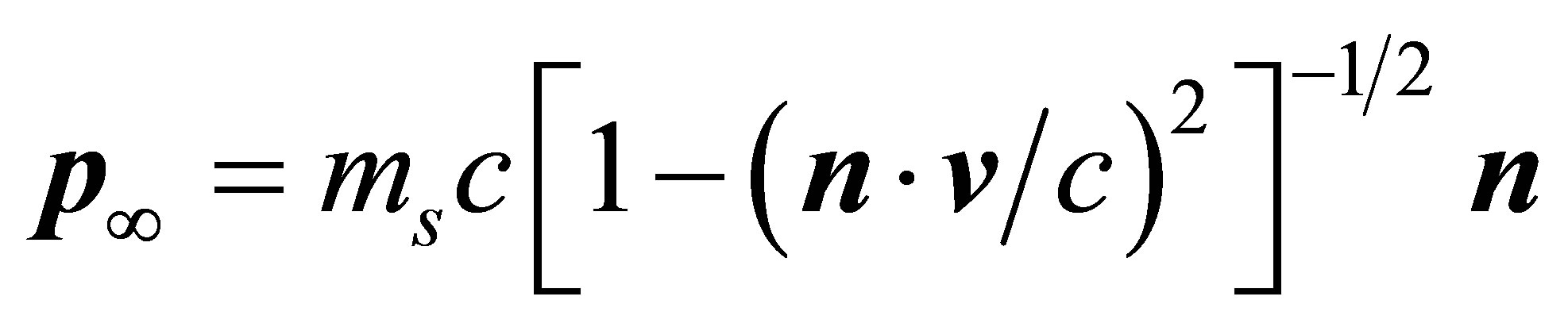(19)
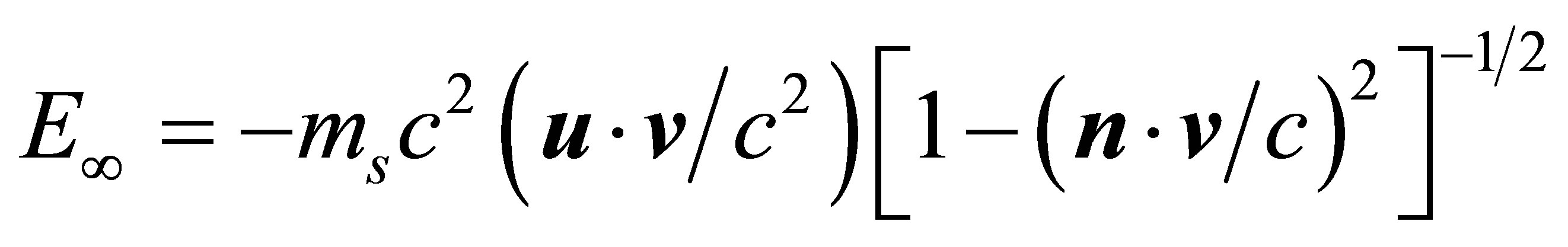(20)
where the unit vector n = u/u. In the preferred inertial frame, v = 0, then the low limit p¥ = mscn, and E¥ = 0. In other inertial frames, the lowest energy might become negative, but it is a limited value, which is different from the old superluminal theory where infinite negative energy was introduced [18]. In Equations (19) and (20), when the unit vector n changes its direction from x to –x, the sigh of (u ×v) is changed. This causes the asymmetric curves in weak-interactions. Because neutrinos are created in a weak-interaction, the asymmetry means that the principle of relativity would be weakly broken in the weak-interaction. This asymmetry is a new consequence under the framework of GGT. Combining Equation (20) with the principle of indeterminacy, the time interval Dt/t will have the same magnitude of DE/E. Considering v/c ≈ 2 × 10-3 from the date of anisotropy in cosmic background radiation [28,29]. The above value is close to the experimental date from CP violation [30].
5. Dirac-Type Equations for Tachyons
Considering neutrinos are superluminal particles, a Dirac-type quantum equation has been discussed in our other papers [31-33]. It is usually to introduce an imaginary mass to consider neutrinos as tachyons, but these efforts could not reach the point of constructing a consistent quantum theory. An alternative approach was investigated by Chodos et al. [34]. A form of the lagrangian density for superluminal neutrinos was proposed, although they did not obtain a satisfactory quantum theory for superluminal fermions. More theoretical work can be found in [35,36].
To follow Dirac’s approach, the Hamiltonian form of superluminal Dirac-type equation for neutrinos can be written in:
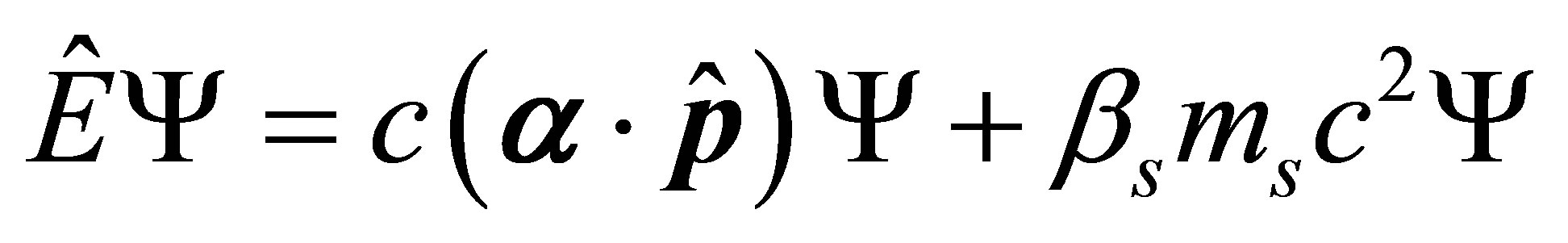(21)
with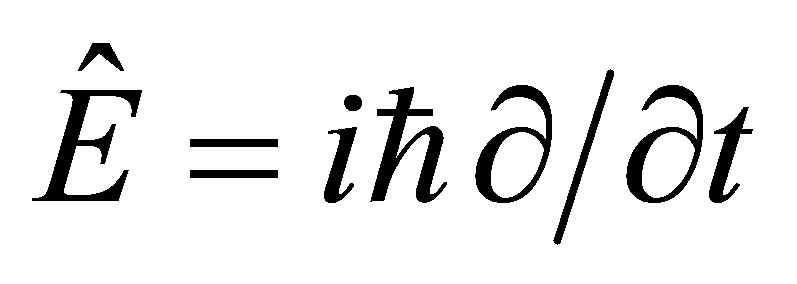
, 
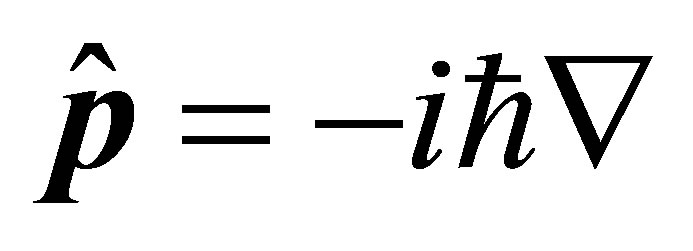and βs are 4 × 4 matrix, which are defined as
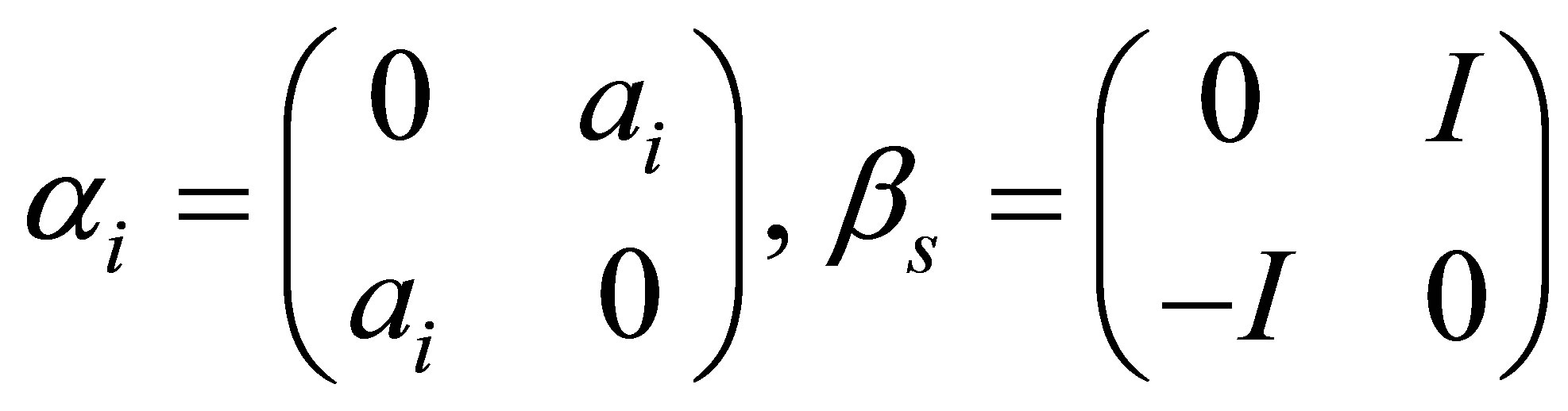(22)
where σi is 2 × 2 Pauli matrix, I is 2 × 2 unit matrix. The commutation relations are as follows:
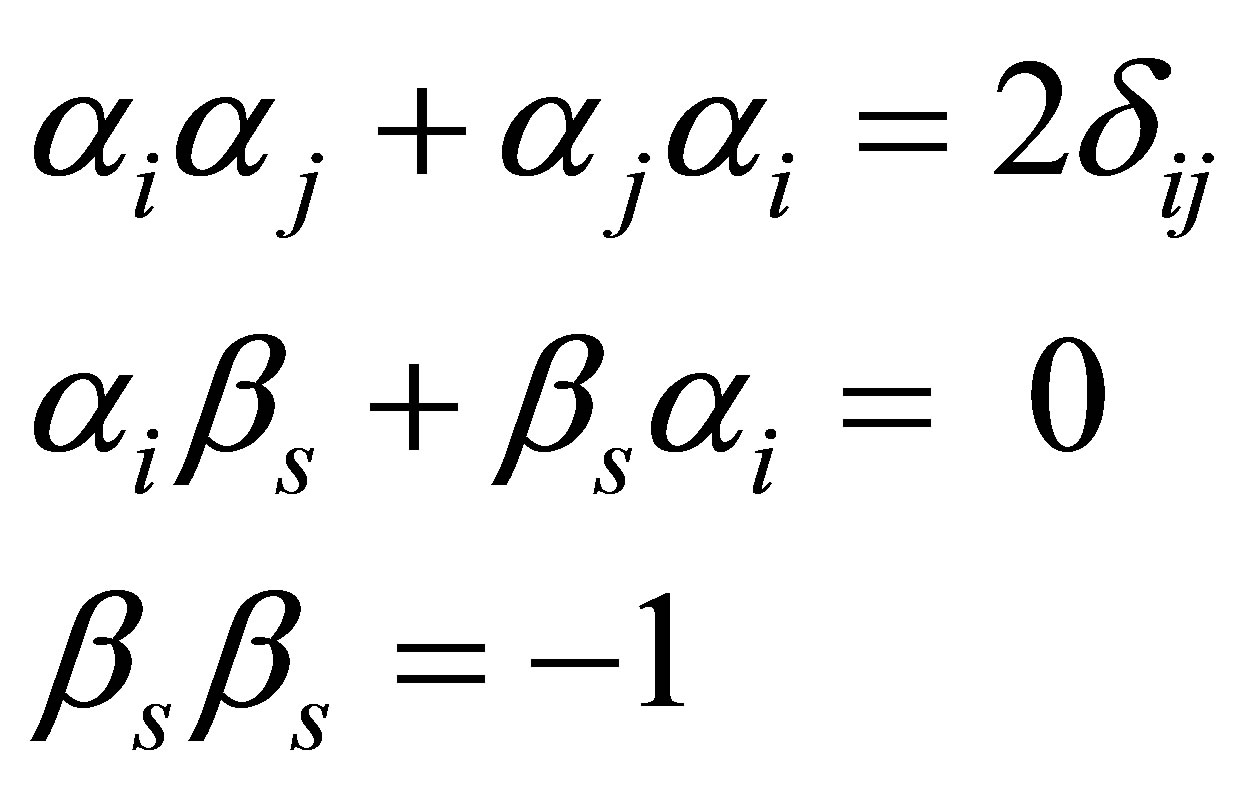(23)
where βs = βγ5. The superluminal Dirac-type Equation (21) can be rewritten in covariant forms by multiplying matrics β and γ5. Denote the bi-spinor function by two spinor functions: ϕ and χ, then Equation (21) can be rewritten as a pair of two-component equations:
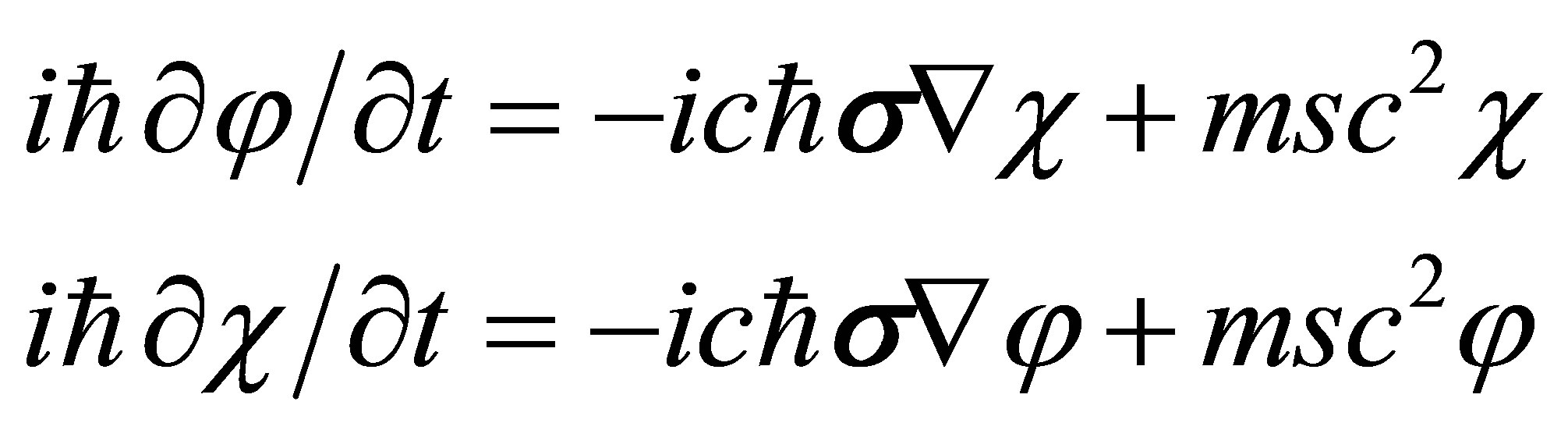(24)
We can get
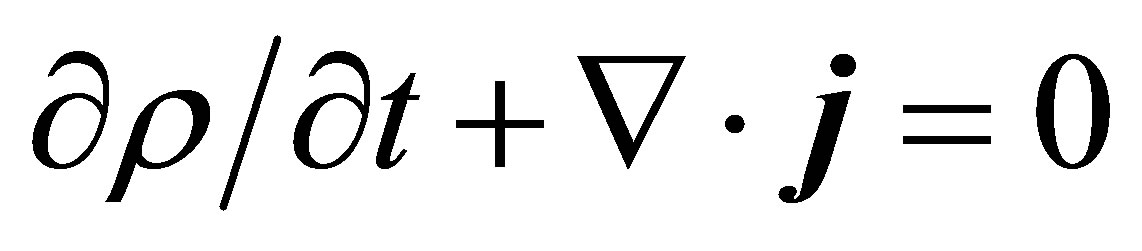(25)
and
,
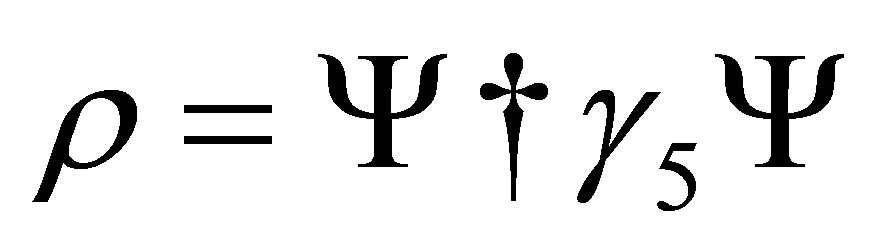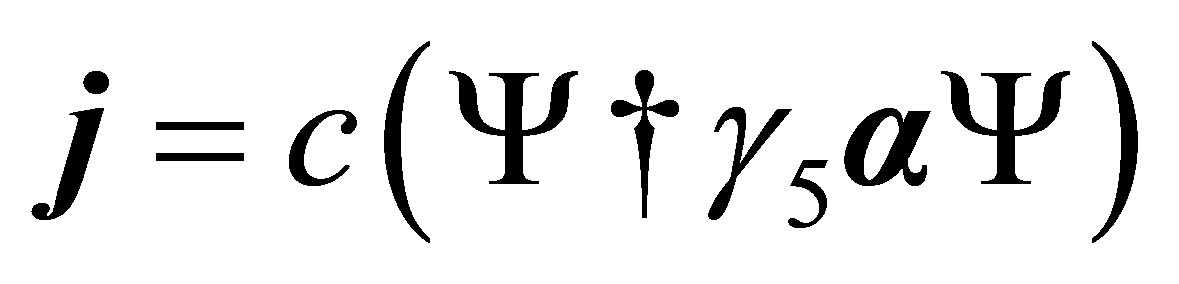(26)
where ρ and j are probability density and current density.; † is the Hermitian adjoint.
6. Conclusions
Based on parity violation in the weak interaction and evidences from neutrino oscillation, a natural choice is that neutrinos may be Superluminal particles with tiny mass. To keep causality for Superluminal particles, a kinematic time under a non-standard form of the Lorentz transformation is introduced.
It has been shown that GGT is a non-standard form of the Lorentz transformation (LT). It means that GGT and LT are equivalent if we describe particles with velocity less than (or equal to) light. On the other hand, when describing superluminal particles, GGT is better than LT. In the framework of GGT, the theoretical difficulties of superluminal motion existing in the traditional theory of special relativity can be removed, such as causality violation, infinite negative energy and others. The GGT framework requires a preferred inertial frame. From observation, the frame defined by the 2.7 K cosmic background radiation might be a good candidate. In dynamics, GGT has obtained the same formula as SR for the relation of energy and momentum.
From the measurement of negative mass-square, neutrinos might be superluminal particles. A Dirac-type equation for Superluminal neutrinos is further investigated, and its solution is brief discussed. This equation can be written in two spins or equations coupled together via tiny mass while respecting maximum parity violation. As a consequence, parity violation implies that the principle of relativity is weakly violated in the weak interaction.
7. Acknowledgements
Thanks are due to Professor D.G. Torr for helpful discussions.