Received 13 July 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT

A numerical scheme based on hybrid central finite-volume and finite-difference method is pre- sented to model Green-Naghdi water wave equations. The governing equations are reformulated into the conservative form, and the convective flux is estimated using a Godunov-type finite vo- lume method while the remaining terms are discretized using finite difference method. To en- hance the robustness of the model, a central-upwind flux evaluation and a well-balanced non- negative water depth construction are incorporated. Numerical tests demonstrate that present model has the advantages of stability preserving and numerical efficiency.

Keywords:

Green-Naghdi Equations, Finite-Volume Method, Solitary Wave

1. Introduction

Water wave is an important dynamic factor in ocean, coastal and port engineering. Accurate simulation of the propagation, breaking and runup of coastal waves has been the research topic for engineers and scientists. Serre [1] derived a one-dimensional system of shallow water equations including frequency dispersion for fully nonlinear and weakly dispersive wave over flat bottom. Green and Naghdi [2] developed the corresponding two- dimensional equations for wave propagation over non-flat bottom topography. Incorporating both weak dispersion and full nonlinearity, the Green-Naghdi equations are applicable to a wide range of problems such as small to large amplitude waves on both shallow and deep water. Until recently, finite difference (FD) method is the main approach to numerically solve Green-Naghdi equations though other methods are also proposed in the literature. Finite volume (FV) method requires significantly less computational effort than the finite element (FE) method and can treat nonlinear advection terms more easily compared to the FD method. However, the application of FV or hybrid FV/FD to fully nonlinear Green-Naghdi is rather limited [3]-[5]. Moving shoreline dominates the wave motion in the swash zone and its accurate simulation is another issue that should be address when developing numerical scheme for Green-Naghdi equations [6].

This paper aims to propose an efficient numerical scheme to 1D Green-Naghdi equations. A hybrid FV/FD scheme is used to solve the governing equations in conservative form. A central upwind scheme is used to com- pute the convective flux, which is simple to implement and free of solving complex Riemann problem, while the rest terms are solved by the FD scheme. Anon-hydrostatic reconstructiontechnique [7] is incorporated to enhance the robustness of the model for dealing with wet-dry fronts. The resulting numerical code is validated for its accuracy and efficiency.

2. Model Description

2.1. Governing Equations

According to [2], the 1D Green-Naghdi equations can be written in the following form

(1)

where d = h + η is the total water depth, h is still water depth and η is the free surface elevation, u is the depth averaged velocity, z_b is the bottom topography and g is the gravity acceleration. The subscripts x and t denote the partial derivative with respect to the spatial variable x and the time variable t. The linear operator T[d, z_b] and the quadratic form Q[d, z_b](・) for arbitrary function ω are defined as

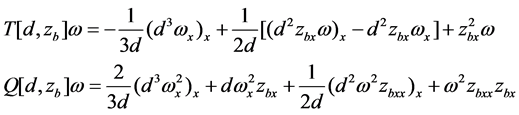(2)

To facilitate the FV method implementation, Equation (1) is rewritten in the following conservative form [6]

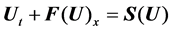(3)

where U is vector variable and F is flux vector along x direction, they are expressed as

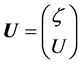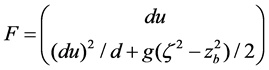,. (4)

with

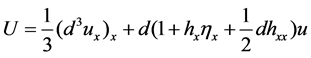. (5)

In Equation (4), a new variable, the water level ζ = z_b + d, is introduced. This rearrangement is done in such a way the linear construction technique proposed by Wang et al. [7] for nonlinear shallow water (NSW) equations can be easily incorporated, which aids present model in handling wet-dry fronts accurately and efficiently. S in Equation (3) is the source vector and can be grouped in three parts namely, bottom slope S_b, bottom friction S_f and dispersive terms S_d

(6)

where the superscript x denotes the value of variable in x direction. And the bottom friction term is expressed as, in which f is the bottom friction coefficient. The dispersive term ψ^x in Equation (6) is written as

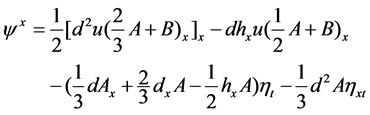(7)

where A = du_x and B = h_xu.

2.2. Well-Balanced Central Finite Volume Method

In present model, the flux terms are solved using Godunov-type FV method while the rest terms are discretized using FD method [6]. The central upwind scheme is used for flux evaluation, which is efficient than the usually used HLL scheme or Roe scheme without the loss of accuracy.

We discretize the computation domain into finite rectangular cells indexed as x_i = i ∆x (i = 1, … M) (M is the gird number in x direction, whereas ∆x is the grid size). Taking the numerical flux through the right-cell interface (F_i+1/2) as an example, its calculation using the central upwind scheme is given by 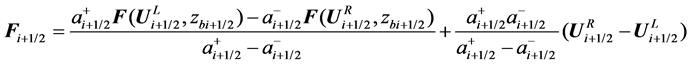[8]

. (8)

where the superscripts L and R denote the left and right states at the cell interface respectively and the one-sided local speeds of the propagation are calculated as

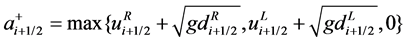(9)

(10)

Evidently, the central upwind scheme is free of solving complex Riemann problem and quite easy to implement than the commonly used upwind Roe, HLL or central MUSTA scheme.

The aforementioned flux calculation method is only first order, which is not sufficiently accurate for approximating the convective flux embodied in Green-Naghdi formulations, hence the fourth-order MUSCLis used for variable construction [6]. The hydrostatic construction technique proposed byWang et al. [7] is used during variable construction to obtain a well-balanced scheme for both wet cells and wet-dry fronts, which helps to capture the moving shore line in an accurate and efficient manner, see [6] and [7] for details.

2.3. Time Integration

The third-order strong stability preserving Runge-Kutta scheme with TVD property is applied to performing time integration of Equation (3). The velocities can then be obtained by solving atridiagonal system, resulting from discretizing Equation (5) using a second-order finite difference formula [6]. The time increment Δt is restricted by the courant number, which is 0.2 for all the simulations.

3. Model Validations and Discussions

3.1. Exact Solitary Wave Propagation

The one-dimensional Green-Naghdi equations have an exact solitary wave solution for horizontal bottom [9], which can be used to test the accuracy of the present numerical scheme.

In this test, the long-time propagation of a highly nonlinear solitary wave with a height of H = 0.6 m over a constant water depth 1.0 m is performed. The computational domain is 450 m in length and discretized with the grid size Δx = 0.10 m. The single solitary wave is initially centered at x₀ = 50 m with the exact surface and velocity profiles and then it propagates from left to right. Bottom friction is neglected and solid wall boundary conditions are used in this simulation.

Figure 1(a) shows the computed results using at different instants t = 0 s, 20 s, 40 s, 60 s and 80 s. The free surface elevations are deliberately shifted to illustrate the evolution of the solitary wave in time. The amplitude

and shape of the solitary wave are well preserved during the long-time propagation, indicating that the governing equations have been correctly discretized and accurately time marched. The computed results at t = 80 s is further compared to the analytical solution in Figure 1(b), they are in excellent agreement.

3.2. Head-On Collision of Two Solitary Waves

This simulation concerns an experiment of collision between two solitary waves propagating in opposite directions (head-on collision), which is described in detail in [10]. Numerical and experimental studies of this problem have been performed by many researchers with different models and numerical methods. The experimental data of this case is only from the carriage window with 1.6 min length as described by Craig et al. [10]. So the computational domain is set 3.6 m long for the simplification and discretized using a grid size of Δx = 0.01 m. The still water depth h is 5 cm. The left wave is initially located at x = 0.5 m with the wave height H₁ = 1.063 cm while the right one is initially located at x = 3.1 m with the wave height H₂ = 1.217 cm.

Figure 2 shows the profiles of the head-on collision at different experimental time. The numerical simulations computed by present model are compared with the experimental data and the numerical simulating results of Li et al. [5]. It shows that there is a very good agreement these three results. The collision wave reaches a maximum height at the time t = 19.50109 s. The wave amplitude during the head-on collision is larger than the sum of the amplitudes of the two incident solitary waves. After the collision, two main waves appear with amplitudes below their initial amplitudes in the beginning. Then they regain amplitude and return to the initial form of two solitary waves when separating from each other finally. As a conscience of the collision, the height of the two forming solitary waves are slightly smaller than the initial amplitudes and the phase has a slightly lag. Meanwhile, there is a small residual from the inelastic nature of the collision.

3.3. Overtaking Collision of Two Solitary Waves

This example concerns the propagation of the collision between two solitary waves travelling in the same direction. The length of computational domain in this case is 13 m and grid size Δx is 0.01 m. Figure 3 displays the overtaking collision at different experimental time. The numerical results obtained from present model are compared with the experimental data form Craig et al. [10] and numerical solution from Li et al. [5]. What should be noted is that the comparison is shown in a relative location along the wave interaction (see [10] for more details). From Figure 3, one can see that the process of this overtaking collision simulation using present model seems to occur faster and the emerging waves have larger amplitude than the experimental data. Despite that, the overall features of the collision shows a good agreement with the experimental data and previous numerical results. Since the overtaking collision expresses a relatively long period of time, it is expected that the accumulated dispersive effects play an important role. Meanwhile, the experimental date after the interaction shows much lower wave amplitude, which is contribute to the dissipative mechanisms in the wave tank [10].

3.4. The Simulation of Solitary Wave Runup

The proposed model is tested for solitary wave runup on a sloping beach following the experimental work of Synolakis [11]. The bottom consists of a plan beach with a slope of 1:19.85.The present model is used to simulate Synolakis’ experimental cases for testing the accuracy of the numerical scheme in modeling solitary wave runup. The experimental data are obtained from [11] and the bed friction coefficient is c_f = 0.001 in all cases. A non-breaking solitary wave run up modeling, the wave amplitude H = 0.0185 m and the still water depth h is 1.0 m.

The length of computational domain is 90 m and the grid size Δx is 0.05 m.

Figure 4 shows the free surface evaluation comparison of the numerical results with experimental data and simulation results by Li et al. at different non-dimensional times t* = t(g/h)^0.5 = 30, 40, 50, 60, 70 from (a) to (e).

One can see that the results computed by present model match the experimental data and previous numerical results well in runup and rundown phases. Differences appear at (e) near the shoreline where the water surface and the sloping beach meet. These differences are likely the consequences of viscous effects [5]. Despite that, the present Green-Naghdi model appears sufficiently to predict the features of non-breaking solitary wave runup on the sloping beach.

4. Conclusion

In this paper, an efficient hybrid central finite volume and finite difference method is proposed to solve the one- dimensional Green-Naghdi equations. The flux terms are discretized using the central upwind flux evaluation which is a simple and free of solving complex Riemann problem. The rest terms are handed with finite difference

scheme. In addition, the hydrostatic reconstruction method is applied to ensure well-balanced and non-negative water depth during computation. The accuracy and efficiency of present model are demonstrated through simulating a series of experiments. The numerical results presented in this paper agree well with the experimental data and the numerical results from other schemes, confirming the capability of the model to simulate coastal water waves accurately and efficiently.

Cite this paper

Kezhao Fang,Zifeng Jiao,Jing Yin,Jiawen Sun, (2015) A Central Numerical Scheme to 1D Green-Naghdi Wave Equations. Journal of Applied Mathematics and Physics,03,1032-1037. doi: 10.4236/jamp.2015.38127

References