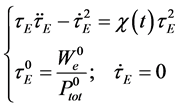Journal of Modern Physics
Vol.07 No.12(2016), Article ID:69653,11 pages
10.4236/jmp.2016.712130
Determination of the Dynamic ITER Energy Confinement Time Scalings
Giorgio Sonnino1,2, Alberto Sonnino3, Jarah Evslin4, Pasquale Nardone1, György Steinbrecher5
1Department of Theoretical Physics and Mathematics, Université Libre de Bruxelles (U.L.B.), Campus Plaine, Brussels, Belgium
2Royal Military School (RMS), Brussels, Belgium
3Ecole Polytechnique de Louvain (EPL), Université Catholique de Louvain (UCL), Louvain-la-Neuve, Belgium
4High Energy Nuclear Physics Group, Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou, China
5Physics Department, University of Craiova, Craiova, Romania

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2016; accepted 8 August 2016; published 11 August 2016
ABSTRACT
We derive the differential equation, which is satisfied by the ITER scalings for the dynamic energy confinement time. We show that this differential equation can also be obtained from the differential equation for the energy confinement time, derived from the energy balance equation, when the plasma is near the steady state. We find that the values of the scaling parameters are linked to the second derivative of the power loss, estimated at the steady state. As an example of an application, the solution of the differential equation for the energy confinement time is compared with the profile obtained by solving numerically the balance equations (closed by a transport model) for a concrete Tokamak-plasma.
Keywords:
Fusion Reactors, Theory, Design, and Computerized Simulation

1. Introduction
Global scaling expressions for the energy confinement time, 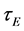 , or the stored energy, W, are powerful tools for predicting the confinement performance of burning plasmas [1] - [3] . The fusion performance of ITER is predicted using three different techniques: statistical analysis of the global energy confinement data in the parameters (simple (multivariate) linear regression tools can be used to determine the parameters from a set of data) [4] [5] , a dimensionless scaling analysis, based on dimensionless physics parameters [5] - [7] , and theory- based on transport models and modelling the plasma profiles [8] - [10] . Although the three methods give overlapping predictions for the performance of ITER, the confidence interval of all of the techniques is still quite wide [11] . The Confinement Database and Modelling Expert Group recommended for ITER design the so-called
, or the stored energy, W, are powerful tools for predicting the confinement performance of burning plasmas [1] - [3] . The fusion performance of ITER is predicted using three different techniques: statistical analysis of the global energy confinement data in the parameters (simple (multivariate) linear regression tools can be used to determine the parameters from a set of data) [4] [5] , a dimensionless scaling analysis, based on dimensionless physics parameters [5] - [7] , and theory- based on transport models and modelling the plasma profiles [8] - [10] . Although the three methods give overlapping predictions for the performance of ITER, the confidence interval of all of the techniques is still quite wide [11] . The Confinement Database and Modelling Expert Group recommended for ITER design the so-called 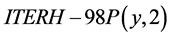 confinement scaling [5] [12] :
confinement scaling [5] [12] :
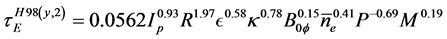 (1)
(1)
Here, the parameters are the plasma current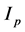 , the major radius R, the inverse aspect ratio
, the major radius R, the inverse aspect ratio 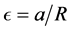 (with a denoting the minor radius of the Tokamak), the elongation
(with a denoting the minor radius of the Tokamak), the elongation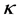 , the toroidal magnetic field (at the major radius R)
, the toroidal magnetic field (at the major radius R)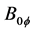 , the central line averaged electron density
, the central line averaged electron density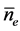 , the loss power P, and the ion mass number M, respectively. The expression (1) is valid for the ELMy H-mode thermal energy confinement time. The 2log-linear interval was determined to be 20%. By recent analyzing the enlarged
, the loss power P, and the ion mass number M, respectively. The expression (1) is valid for the ELMy H-mode thermal energy confinement time. The 2log-linear interval was determined to be 20%. By recent analyzing the enlarged 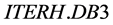 dataset, the practical reliability of the
dataset, the practical reliability of the 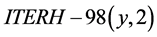 scaling was confirmed and 2log-linear interval was reduced to 14% [13] . Tables showing some of the most generally used sets of scaling parameters for the ELMy H-mode and L-mode can be found in Refs [5] [14] - [16] .
scaling was confirmed and 2log-linear interval was reduced to 14% [13] . Tables showing some of the most generally used sets of scaling parameters for the ELMy H-mode and L-mode can be found in Refs [5] [14] - [16] .
For stellarators, a similar scaling has been obtained [17] [18]
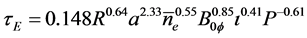 (2)
(2)
where 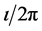 is the rotational transform (or the field line pitch).
is the rotational transform (or the field line pitch).
The confinement time is defined as
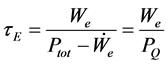 (3)
(3)
where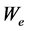 ,
, 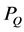 and
and 





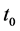

The main objective of this work is to estimate the energy confinement time, close to the steady state. 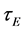
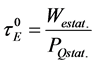
where 

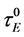


where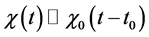
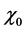


In this work, we shall also justify the dynamic scaling laws, like
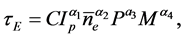
where C is a constant and M is the effective mass, respectively (note that when the plasma is a mixture, due to the dependence of particle transport properties on particle mass and charge, M is also time dependent). In particular, we shall prove that the dynamic expression for the energy confinement time, like Equation (6), is solution of the differential equation for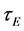
The paper is organized as follows. In Section (2), we show that Equation (6) satisfies a nonlinear differential equation of the second order in time, tacking into account the (experimentally established) slow variation in time of the coefficient entering in this equation. Successively, we show that this equation can also be derived from the energy balance equation, combined with definition (3). This will allow a linking of the scaling coefficients with the (measurable) second time derivatives of the heat power loss, which at the leading order may also be estimated at the stationary state. These tasks will be accomplished in the Section (3). As an example of an application, in the Section (4), we compare the solution obtained by solving the differential equation for the energy confinement time with the numerical simulations obtained using the code JETTO [20] , for the specific case of IGNITOR-plasmas. Concluding remarks can be found in Section (5).
2. Differential Equation Satisfied by the ITER Scalings
The expression for the energy confinement time, obtained by scaling laws, raises several questions. Firstly, Equation (1) applies quite well to a large number of Tokamaks (ASDEX, JET, DIII-D, ALCATOR C-Mod, COMPASS, etc.) and it is currently used for predicting the energy confinement time for Tokamaks, which are presently in construction (ITER) or will be constructed in the future (DEMO). Hence, the first objective of this work is to understand the main reason for such a “universal” validity. Secondly, it is legitimate to ask “where does this expression originate from ?”. More concretely, “Is it possible to determine the (minimal) differential equation which is satisfied by expression (6)?”. In case of a positive answer, “Is it possible to re-obtain this (minimal) differential equation from the balance equations and, in particular, from the energy balance equations ?”. Finally, “How can we estimate the values of the scaling coefficients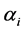
The equations of one-dimensional plasma dynamics, in toroidal geometry, assuming the validity of the standard model, can be brought into the form (see, for example, [21] )

with r and 
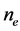
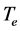



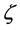






with

where the “dot” over the variables stands for the (total) time derivative (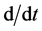
The energy confinement time is defined as
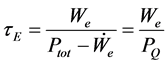
From definition (10), we find

Note that the stationary state is reached when


At the steady state, we find

where 

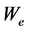

Equation (6) may be re-written in the generic form:

where 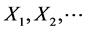





Unless stated otherwise, in the sequel we shall adopt the summation convention on the repeated indexes. By taking the logarithm of Equation (14) we find
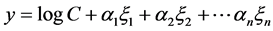
with 
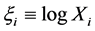
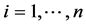


In terms of variable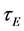

The differential equation with respect to time is easily obtained by tacking into account the identities

By multiplying the second equation of Equation (18) by 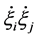

Equation (20) should be solved with the initial conditions (13):
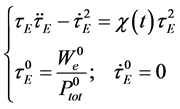
with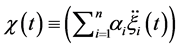
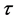
equation of Equation (19) which is first order and also Equation (20) which is second order. It may appear hopeless to solve these equations, as they depend on 



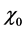


It is not difficult to check that the nonlinear Equation (21) is the “minimal” differential equation, in the sense that Equation (21) admits one, and only one, solution (i.e., the nonlinear differential Equation (21) does not generate additional solutions).
It may appear hopeless to solve Equation (21), as it depends on the coefficient
turn depend on the full dynamics of the system. The critical fact which makes our approach useful is that the second time derivatives of the logarithm of 
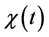
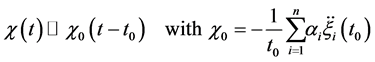
Hence, all of the dependence on the machine is reduced to just a number, 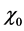
3. Differential Equation for the Energy Confinement Time
The aim of this Section is to obtain the differential equation for the energy confinement time from the balance equations. In analogy with Equation (21), the coefficients of this differential equation should be expressed only in terms of the internal energy 
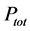

with

Note that the dimensions of 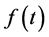


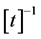
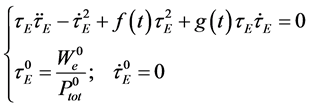
We might object that the previous equation has the same degree of difficulty as the initial expression, Equation (10). However, as we shall see more in detail in the next Subsection, the coefficients 

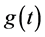
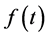
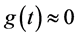
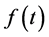
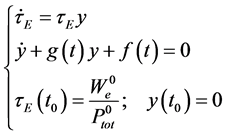
showing that the differential equation for the energy confinement time may be expressed as two quasi-decoupled differential equations of first order in time derivative. The general solution of Equations (26) may be brought into the form
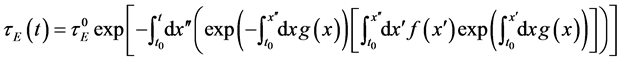
By taking into account that 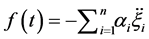
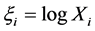
laws out of the steady state, reducing to Equation (14) close to the stationary state. Equation (27) shows that close to the steady state, the leading contribution to the mathematical expression for the energy confinement time is provided by the power laws. However, when we deviate from the steady state, supplementary con- tributions, which are different from the power ones, may modify the mathematical form of the power laws significantly. Generally, for ITER, these contributions tend to lower the numerical value of the energy con- finement time. This can be easily checked by setting in Equation (27)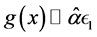
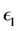
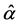
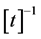


・ Differential Equation for the Energy Confinement Time Near the Steady State
The term 
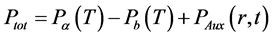
where 

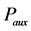


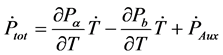
At the steady state 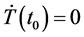

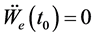
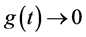
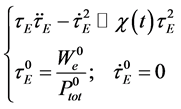
with
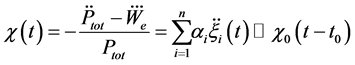
where Equation (22) has been used. As shown in the Section (2), Equation (30) admits one (and only one) solution, corresponding to the ITER scalings Equation (6). Note that Equation (31) provides the desired relation between the exponent coefficients 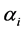

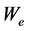
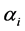
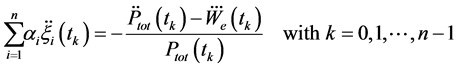
Equation (32) link the exponent coefficients with variables which, at least in principle, are under the control of the experimental physicist.
・ Analysis in the “Physics” Variables
As mentioned, Equations (1) and (2) are composed by several variables independent of time (e.g., major and minor radii, elongation etc.). In this case, it is more convenient to express the energy confinement time only in terms of the time-dependent variables. Let us suppose that m variables are time-dependent and the remaining 
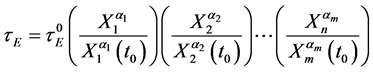
where, now, the independent variables 
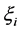



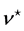
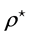
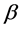
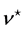

with 

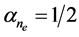
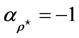
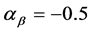
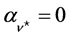
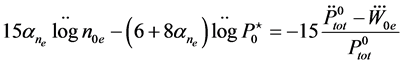
where Equation (33) has been taken into account. We find
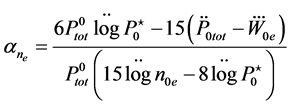
4. Comparison with the Numerical Simulation of the Balance Equations for an L-Mode Tokamak-Plasma
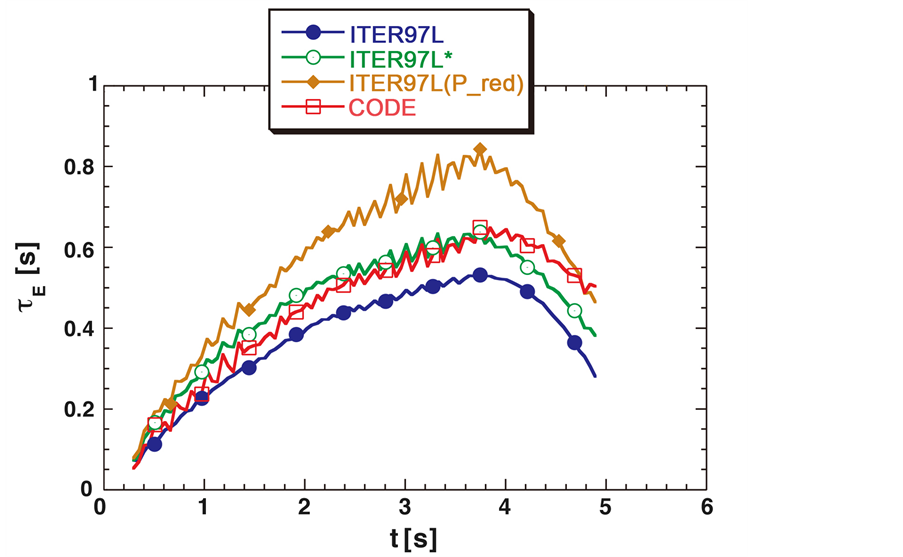
As an example application, we consider in this Section the case of one of the simplest L-mode Tokamak-plasma where the evolution of the energy confinement time has been estimated by solving numerically the balance equations, completed with a transport model. In [20] we find the profile of 
solution of Equation (21), we should firstly estimate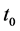

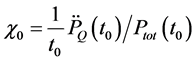
and (24)]. In [19] , we have estimated the values of these parameters for Ignitor subject to ICRH power (i.e.,
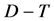
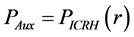
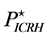
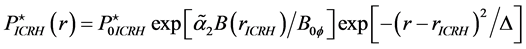
with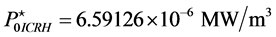
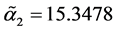
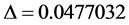
The value of 

with 


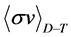
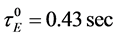

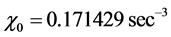


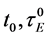



Note that in [20] the authors evaluate the ITER scalings by using the reduced power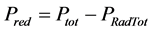

5. Conclusions
A large database on plasma energy confinement in Tokamaks can be summarized in single empirical value of


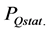
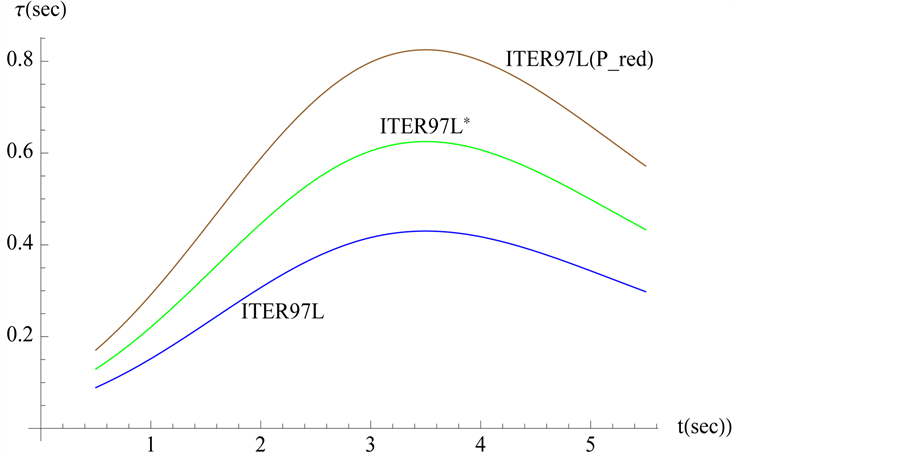
Figure 1. Solutions of Equation (21) at the three values of




Figure 2. Energy confinement time evolution estimated in [20] by solving with JETTO the balance equations (completed with a transport model): ITER97L scaling (full dots-blue line), 
time, we determined the differential equation for 
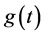
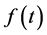

where “at the leading order” 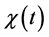

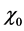

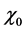
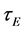

Acknowledgements
Giorgio Sonnino is very grateful to Dr Philippe Peeters for his useful suggestions. Jarah Evslin is supported by NSFC MianShang grant 11375201. The reproduction of Figure 2, reported in Ref. [20] , has been authorized by the review Nuclear Fusion (IoP).
Cite this paper
Giorgio Sonnino,Alberto Sonnino,Jarah Evslin,Pasquale Nardone,György Steinbrecher, (2016) Determination of the Dynamic ITER Energy Confinement Time Scalings. Journal of Modern Physics,07,1429-1439. doi: 10.4236/jmp.2016.712130
References
- 1. Kardaun, O.J.W.F. (2005) Classical Methods of Statistics: With Applications in Fusion-Oriented Plasma Physics. Springer Science & Business, Heidelberg.
- 2. Tsunematsu, T. (1991) Fusion Engineering and Design, 15, 309.
http://dx.doi.org/10.1016/0920-3796(92)90016-W - 3. Doyle, E.J., Houlberg, W.A., Kamada, Y., Mukhovatov, V., Osborne, T.H., Polevoi, A., Bateman, G., Connor, J.W., Cordey, J.G., Fujita, T., Garbet, X., Hahm, T.S., Horton, L.D., Hubbard, A.E., Imbeaux, F., Jenko, F., Kinsey, J.E., Kishimoto, Y., Li, J., Luce, T.C., Martin, Y., Ossipenko, M., Parail, V., Peeters, A., Rhodes, T.L., Rice, J.E., Roach, C.M., Rozhansky, V., Ryter, F., Saibene, G., Sartori, R., Sips, A.C.C., Snipes, J.A., Sugihara, M., Synakowski, E.J., Takenaga, H., Takizuka, T., Thomsen, K., Wade, M.R. and Wilson, H.R., ITPA Pedestal (2007) Nuclear Fusion, 47, S18.
- 4. Wagner, F. (2009) The Physics Basis of ITER Confinement. 2nd ITER Int. Summer School (Kyushu University, Japan, 2009) (New York: AIP) AIP Conf. Proc., 31, 1095.
http://dx.doi.org/10.1063/1.3097319 - 5. ITER Physics Expert Groups on Confinement and Transport and Confinement Modelling and Database, ITER Physics Basis Editors and ITER EDA, Naka Joint Work Site, Mukouyama, Nakamachi, Nakagun, Ibaraki-Ken, Japan (1999) Nuclear Fusion, 39, 2137.
- 6. Luce, T.C., Petty, C.C. and Cordey, J.G. (2008) Plasma Physics and Controlled Fusion, 50, 043001.
- 7. Kadomtsev, B.B. (1975) Soviet Journal of Plasma Physics, 1, 295.
- 8. Kritz, A.H., Kinsey, J., Onjun, T., Voitsekhovich, I., Bateman, G., Waltz, R. and Staebler, G. (2001) Burning Plasma Projections with Internal Transport Barriers. ITPA Meeting on Burning Plasma Transport, NIFS, Tokio, 10-12 September 2001, 964-974.
- 9. Weiland, J. (2001) Predictive Simulations of ITER-FEAT Performance. 28th EPS Conference, Madeira, 18-22 June 2001, P2.039.
- 10. Bateman, G., Kritz, A.H., Onjun, T. and Pankin, A. (2001) Private Communication, 7 Dec.
- 11. Cordey, J.-G. (1997) Plasma Physics and Controlled Fusion, 39, B115.
http://dx.doi.org/10.1088/0741-3335/39/12B/009 - 12. Scaling Law, FusionWiki, jointly hosted by LNF and FuseNet. It is associated with two domains: fusionwiki.ciemat.es (http://fusionwiki.ciemat.es/wiki/Scaling_law) and wiki.fusenet.eu.
- 13. Kardaun, O. (2002) Nuclear Fusion, 42, 841.
http://dx.doi.org/10.1088/0029-5515/42/7/307 - 14. Cordey, J.G., Snipes, J.A., Greenwald, M., Sugiyama, L., Kardaun, O.J.W.F., Ryter, F., Kus, A., Stober, J., DeBoo, J.C., Petty, C.C., Bracco, G., Romanelli, M., Cui, Z., Liu, Y., Cordey, J.G., Thomsen, K., McDonald, D.C., Miura, Y., Shinohara, K., Tsuzuki, K., Kamada, Y., Takizuka, T., Urano, H., Valovic, M., Akers, R., Brickley, C., Sykes, A., Walsh, M.J., Kaye, S.M., Bush, C., Hogewei, D., Martin, Y., Cote, A., Pacher, G., Ongena, J., Imbeaux, F., Hoang, G.T., Lebedev, S., Chudnovskiy, A. and Leonov, V. (2004) IAEA 20th Fusion Energy Conference, Vilamoura, paper IAEA-CN-116/IT/P3-32.
- 15. Yushmanov, P.N., Takizuka, T., Riedel, K.S., Kardaun, O.J.W.F., Cordey, J.G., Kaye, S.M. and Post, D.E. (1990) Nuclear Fusion, 30, 1999.
http://dx.doi.org/10.1088/0029-5515/30/10/001 - 16. Kaye, S.M., Greenwald, M., Stroth, U., Kardaun, O., Kus, A., Schissel, D., DeBoo, J., Bracco, G., Thomsen, K., Cordey, J.G., Miura, Y., Matsuda, T., Tamai, H., Takizuda, T., Hirayama, T., Kikuchi, H., Naito, O., Chudnovskij, A., Ongena, J. and Hoang, G. (1997) Nuclear Fusion, 37, 1303.
http://dx.doi.org/10.1088/0029-5515/37/9/I10 - 17. Dinklage, A., Maaβberg, H., Preuss, R., Turkin, Yu.A., Yamada, H., Ascasibar, E., Beidler, C.D., Funaba, H., Harris, J.H., Kus, A., Murakami, S., Okamura, S., Sano, F., Stroth, U., Suzuki, Y., Talmadge, J., Tribaldos, V., Watanabe, K.Y., Werner, A., Weller, A. and Yokoyama, M. (2007) Nuclear Fusion, 47, 1265.
- 18. Yamada, H., Harris, J.H., Dinklage, A., Ascasibar, E., Sano, F., Okamura, S., Stroth, U., Kus, A., Talmadge, J., Murakami, S., Yokoyama, M., Beidler, C.D., Tribaldos, V. and Watanabe, K.Y. (2004) 31st EPS Conference on Plasma Physics, London, 28 June-2 July 2004, ECA Vol. 28G, 5.099.
- 19. Cardinali, A. and Sonnino, G. (2014) Analysis of the Thermonuclear Instability Including Low-Power ICRH Minority Heating in IGNITOR. Submitted for publication in EPJD.
- 20. Airoldi, A. and Cenacchi, G. (2001) Nuclear Fusion, 41, 687.
http://dx.doi.org/10.1088/0029-5515/41/6/303 - 21. Balescu, R. (1988) Transport Process in Plasmas—Vol. II. Elsevier Science Publication, North-Holland.
- 22. Kadomtsev, B.B. (1975) Soviet Journal of Plasma Physics, 1, 295.
- 23. Sauter, O. and Martin, Y. (2000) Nuclear Fusion, 40, 955.
http://dx.doi.org/10.1088/0029-5515/40/5/308