ABSTRACT

Recovery by Equilibrium in Patches (REP) is a recovery method introduced by B. Boroomand. This method is using patch as recovery media as is used by Superconvergent Patch Recovery (SPR) which is well known as a good recovery method. In this research, a numerical study of REP implementation is held to estimate error in finite element analysis using DKMQ element. The numerical study is performed with both uniform and adaptive h-type mesh refinement. The result is compared with three other recovery method, i.e. SPR method, averaging method, and projection method.

1. Introduction

Solution error is unavoidable in finite element method application, either caused by inappropriate model, numerical integration usage, inaccuracy of numerical solution, or rounding error accumulation in numerical process. A complex problem usually has no exact solution, therefore, the error happened is also difficult to determine. Error estimator is developed to gain solution as close as possible compared to exact solution.

Error estimation procedure based on recovery method gives good result for various plate problem. A widely used error estimator is superconvergent method which has known giving high error convergence rate. The first superconvergent method is Superconvergent Patch Recovery (SPR) method which is developed by ZienkiewiczZhu [1,2]. The basic principle of this method is recovering element nodal forces by least square fit method analogy on some internal force sample which is known more accurate.

A study developed by Zhang [3] showed that the Zienkiewicz-Zhu patch recovery technique gives ultraconvergent result when even-order finite element spaces and local uniform meshes are used.

The next super-convergent method is Recovery by Equilibrium in Patches (REP) which is developed by Boroomand [4-6]. This method is based on equilibrium of solution formulation to produce recovered internal forces field. Like SPR, REP uses patches as calculation media.

Estimation error a posteriori continues to develop because it is more easily and efficiently.

Zhang [7] in 2004 named the method as a method of Polynomial Preserving Gradient Recovery, sometimes referred as the Polynomial Preserving Recovery (PPR).

Zienkiewicz O.C. [8] in 2006 summarized the present state of the art concerning error estimation and adaptive re-meshing in finite element computation. He found that the residuals of the original solution need not be calculated to obtain the best answers, because process of recovery has important role in error estimation and its accuracy.

Duster [9] in 2007 presented a pq-adaptive finite element procedure for three-dimensional computation of thinwalled structures. He used for the application plates and shells and this approach is using the hexahedral element with high-order shape functions.

Destuynder [10] in 2008 presented a strategy concerning mesh refinements for thin shells computation especially adaptive mesh refinements for thin shells whose middle surface is not exactly known.

Ainsworth [11] in 2009 gave an overview of recent progress in developing a framework for the derivation of fully computable guaranteed posteriori error bounds for finite element approximation. He focused his study on conforming, non-conforming, mixed and discontinuous finite element schemes.

Nie [12] in 2009 found that the CPU time cost greatly increases if we use the overall mesh refinement thus the adaptive mesh is refined only in the localization region.

Lukin [13] in 2011 used the HiFi/SEL high-order finite element code to study the effects of various mesh distortions on solution quality of analytic problems. He uses the problems for spatial discretizations with different order of finite elements. He found that the total error increases with the degree of distortion.

Bathe [14] in 2011 introduced a novel approach of stress calculations in finite element analysis using the element nodal point forces. It is very simple than using the stress assumption employed in establishing the stiffness matrix. Also, it is very simple to enhance the finite element stress predictions at a low computational cost.

In this paper, a comparative study is held to evaluate the several stress recovery method in estimating error of finite element result using DKMQ (Discrete Kirchoff Mindlin Quadrilateral) element [15], which has been acknowledged internationally and implemented in commercial software of MIDAS. The performance of REP is then compared with other method, i.e. SPR method, projection method and averaging method.

2. The Recovery Method

While FEM solution has been known to give continuity in displacement at nodal points, it yields discontinuity and inaccuracy problems when used to calculate internal forces at joined sides of the boundary elements [16]. By theory or analytical solution, the problem should not happen as adjacent elements maintains uniformity in form and characteristics. Yet, the nature of FEM solution which calculates internal forces using the derivation of displacement function has created such problem (Figure 1).

Displacement continuity resulted by FEM solution at nodal points does not occur to the internal forces at joined sides of the boundary elements. These internal forces are calculated from the derivation of displacement function which causes problems in continuity and accuracy. By theory or analytical solution, the problem should not happen as the geometry maintains the continuity of shape. This problem occurs in the finite element method that later being the basic approach for estimating the error of finite element calculation.

2.1. The Averaging Method

The recovery is taken from the average value of finite element result in each element.

and   (1)

where and are recovered moment and shear forces, and are finite element result of moment and shear forces in node i, while m is number of elements consisting node i.

2.2. The Superconvergent Patch Recovery (SPR)

Superconvergent Patch Recovery method is relative simple and easy-used. The idea is recovering finite element result with least square fit method analogy.

The recovered moment/shear force is assumed as

(2)

where is polinomial expansion function in parametric local coordinate system which assumed as continuous stress field in evaluated patch (Figure 2). The unknown parameter {a_n} is solved by minimizing the following function

(3)

where is Gauss coordinat in patch local coordinate system, n is number of Gauss point in patch, is finite element result.

The minimization yields

(4)

and

(5)

where

(6)

2.3. The Recovery by Equilibrium in Patches (REP)

The Recovery by Equilibrium in Patches uses a weighted form of equilibrium equation to produce recovered solution.

The equilibrium equation of patch is expressed as

(7)

This leads us to a simple requirement that the recovered values satisfy approximately

(8)

Where:

(9a)

(9b)

Hence, Equation (8) can be expressed as:

(10a)

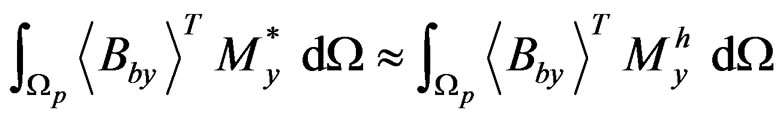(10b)

(10c)

(10d)

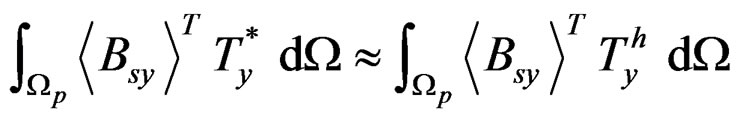(10e)

As an example, in recovering, substituting Equation (2) to Equation (10a) will produce:

(11)

Using Gauss numerical integration, Equation (11) can be expressed as:

(12)

with n is the number of element’s Gauss integration points which included in patch, J is Jacobian matrix and ω is weighting factor.

Equation (12) can also be expressed as

(13)

Where

and          (14)

with m is number of elements in a patch, and

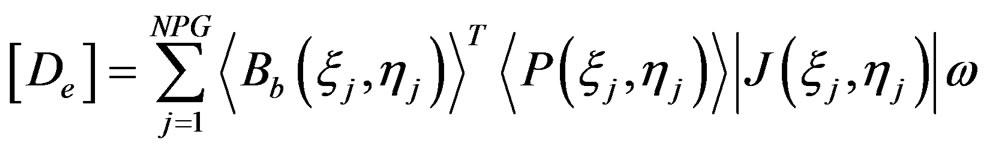(15)

(16)

with NPG is number of Gauss points in each element in a patch, and n = m × NPG. Then, using least square fit method, we define the following function

(17)

And minimizing it to, yields

(18)

In some patch configuration, [D] is probably unstable. This problem can be solved by defining function

(19)

Minimizing that equation to {a_n} will produce:

(20)

or

(21)

with

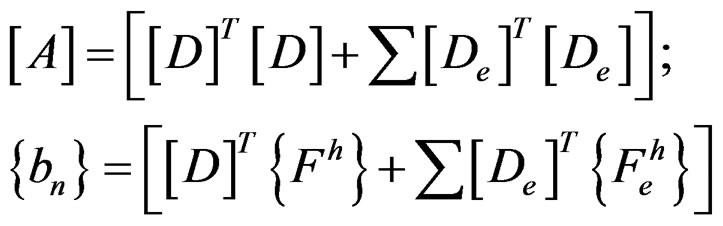; (22)

In above, and have the same expression as and, but the integrals are applied on each element.

2.4. Error Indicator and Refinement

Error estimation will become actual error if element size is set to be very small so as to approach zero, which creates infinite number of elements. Since calculation will never stop if element size is close to zero, we need an effective condition as criteria to terminate discrete process.

Indicator for exact error of a structure is defined by exact error of energy norm that is normalized by exact strain energy norm:

(23)

where is error in energy norm from this equation

(24)

= total exact error in energy norm and m = number of element in structure while is twice as much as exact strain energy of the whole structure, which for plate structure consists of bending and shear energy.

The above indicator can be computed only if exact solution is available which can be estimated by recovering the solution as discussed before.

Indicator for relative error f^* of a structure with recovery method is:

(25)

Value of is obtained from:

; (26)

Error indicator represents value used as criteria to terminate the refinement process. This can be done by setting a condition for, that is whenever then the refinement process will stop. Generally, the value of is taken to be 5%. The permitted error indicator for structure is determined by:

(27)

where is permitted error of global energy norm, given by:

(28)

In an optimal element mesh, distribution of error of energy norm is uniform in all elements, thus:

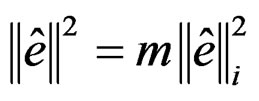(29)

where: m = number of element.

And then, we have:

(30)

Thereby we can set a condition that error in every element i must be equal to or less than:

(31)

where: = permitted error of energy norm estimated for each element i.

Element whose error exceeds the permitted value most probably will be refined. Let us set a ratio:

An element must be refined if:

3. Numerical Study

The following notation is used in the numerical study.

REP1: REP method, element based patch, minimum 3 elements in one patch.

REP2: REP method, element based patch, minimum 5 elements in one patch.

REP3, REP: REP method, element based patch, minimum 7 elements in one patch.

SPR1: SPR method, nodal based patch.

SPR2: SPR method, element based patch.

NELT: number of elements.

A study is held subjected to circular plate under uniform load (Figure 3). The study implements REP methods and covers various patch configurations as classified above. The result shows that all patch configuration give accurate result and close to other recovery methods for moment recovery.

However, external patch usage, happened if we allow minimum 3 or 5 elements in one patch (REP1 and REP2), may produce inaccurate result for shear force (Figure 4). Meanwhile, using only internal patches, which have minimum 7 elements in one patch, gives better result for shear force.

Figure 4 shows that external patches produce very large different results for shear force in the center of the plate. Approaching plate edge/support, the difference between REP1, REP2 and REP3 becomes smaller, but the result differs quite significant compared to other method’s result. It is widely known that bending plate element like DKMQ is developed with an aim to solve shear locking problem, hence, shear force accuracy is not considered important (Figure 5 and Figure 6).

The circular plate study is also analyzed for various plate thickness, including thin and thick plates, with R/h varied from 50, 5, and 2. The study shows similar accuracy characteristic for all R/h (Figure 7 and Figure 8). External patches usage for all R/h values produces inaccurate result for shear force in plate center.

In this numerical study, relative error indicator is studied for various element numbers, i.e. 3, 12, 27, and 48 elements. For thin plate (R/h = 50), all patch configuration including external patch give close relative error indicator result compared to SPR method result (Figure 9). However, for thicker plate with R/h equal 5 and 2 (Figure 10 and Figure 11), only full internal patch usage (REP3) gives very close result compared to SPR, while other patch configurations give fluctuant result. Based on this result, it can be concluded that only full internal patch usage is reliable and hence, for other study, only this patch configuration will be applied for REP method.

Another way to obtain good relative error indicator result is to consider only bending error indicator partially. Partial relative error indicator for bending gives no fluctuant result (Figures 12-14).

The next numerical study is held on fixed supported rectangular plate under uniform load (Figure 15). Uniform mesh refinement is used with 2 × 2, 4 × 4, 8 × 8 and 16 × 16 meshing. Moment recovery is studied at the plate center and at the support. The study shows that REP method gives super convergent result (Figures 16-18).

At plate center, 2 × 2 mesh of REP method gives quite high error percentage, but the result converges rapidly which is less than tolerance limit 5% for only 4 × 4 mesh.

With the same meshing, SPR1 (nodal based patch) has reached that tolerance limit, but SPR2 (element based patch), projection method and averaging method give higher value than tolerance limit.

At plate support, 4 × 4 mesh of REP method still gives much high error percentage (24.5%), but 16 × 16 mesh gives almost exact solution (0.01%) which is much better compared to SPR and averaging method. In this case, projection method gives very poor result compared to others. 

Total relative error indicator produced by REP method shows close result to SPR1, SPR2, and averaging method, while projection method gives poorer result.

Circular plate as shown in Figure 19 is also studied for both uniform and adaptive mesh refinement. The uniforrn mesh refinement scheme is shown in Figure 20 and the adaptive mesh refinement is shown in Figure 21. It has been shown that adaptive mesh refinement gives better result than uniform one. For both refinements, for either fixed nor simply supported circular plate, REP method gives super convergent result, close to SPR result (Figures 22 and 23 for uniform mesh refinement and Figures 24 and 25 for adaptive mesh refinement). REP’s total error indicator for both refinements and both support types are closed to those of SPR1, SPR2 and averaging method, which are much better than that of projection method.

4. Conclusions

Patch type usage is sensitive in REP application. External patches usage gives fluctuant result in shear force recovery in REP application, hence, only internal patches are recommended. External patch usage still gives similar REP relative error indicator for thin plate, but gives higher relative error indicator for thick plate. Full internal patch usage does not give significant REP relative error indicator difference for both thin and thick plates.

Partial relative error indicator for bending gives good result without any fluctuant result for various element numbers.

REP method gives very close result compared to SPR method. Generally, both REP and SPR give better result than averaging and projection method.

5. Acknowledgements

The writer would like to thank to the Indonesian Ministry of National Education, Directorate General of Higher Education (MNE-DGHE) and French Embassy in Jakarta for the research grant given to the writer in the project of International Joint Research between Universitas Indonesia (UI), Indonesia and Université de La Rochelle (ULR), France.

REFERENCES