Open Journal of Fluid Dynamics
Vol.2 No.4A(2012), Article ID:26368,6 pages DOI:10.4236/ojfd.2012.24A044
Transient Hydraulic Performance and Numerical Simulation of a Centrifugal Pump with an Open Impeller during Shutting Down
1The State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou, China
2The Province Key Laboratory of Fluid Transmission Technology, Zhejiang Sci-Tech University, Hangzhou, China
Email: *zhang002@sina.com
Received September 30, 2012; revised November 12, 2012; accepted November 21, 2012
Keywords: Centrifugal Pump; Straight Blade; Shut Down; Negative Impulsion; Flow Inertia
ABSTRACT
In this paper, the transient behavior of a low specific speed centrifugal pump with straight blades during shutting down is studied through the experimental test, theoretical calculation, and numerical simulation. The variations of the rotational speed, flow rate, and head with time are obtained in experiment. Based on the experimental results of the rotational speed and flow rate, the additional theoretical heads are quantitatively calculated and analyzed. The experimental results of the rotational speed and flow rate are worked as the boundary conditions to accurately accomplish the numerical simulation of the transient flow during shutting down. The experimental results show that the decrease history of the flow rate evidently lags behind that of the rotational speed, while the rotational speed slightly lags behind the head. Theoretical analysis shows that there exists a clear negative head impact phenomenon in the process of stopping. The transient behavior of the centrifugal pump with straight blades mainly comes from the rotation deceleration of impeller, and has nothing to do with the fluid deceleration. The numerical simulations show that a large area backflow can be seen when the rotational speed decreases to zero due to the flowing inertia. In conclusion, the numerical simulation of the flow field is in good agreement with the internal flow theory of centrifugal pumps.
1. Introduction
Centrifugal pumps are liable to malfunction when working at unstable states, such as startup and stopping. Meanwhile, the study on transient behavior is very limited by far. The main characteristics of these transient problems are as follows: very short time, intense variation, and unsteady flow. Startup and shut down of fluid machinery are unsteady transient flow problems caused by the movement of the wall. Some researches have shown that transient effect is very obvious during startup [1-6], the distinction between stable and unstable states is evident. Presently, the research on transient behavior has basically concentrated on the startup process of centrifugal and mixed flow pumps, while the studies of the transient behavior of shut down are few. Wang [7] researched the shut down of a mixed flow pumps. These results show the head, flow rate and energy of the piping system rapidly decline during shut down, and proposed an operation method for shut down. Tsukamoto [8] researched the shut down of a centrifugal pump by experimental test and theoretical analysis, his results show that the initial pressure coefficient is greater then falls below the quasistable state value.
With the development of wider application field, it is more necessary to study the interior flow characteristics of centrifugal pumps to reveal their transient performance. As is well known, the instantaneous rotational speed, flow rate, and pressure quickly vary with time during shut down. If these conditions are worked as boudary conditions in simulation, the flow calculation can be accomplished. Therefore, in this work, a calculation mothod is adopted—numerical simulation based on experimental results. In this method, the rotational acceleration is taken into account and experimental results (rotational speed, flow rate etc.) are defined as time functions, which are then written to program by user defined function (UDF). The method can accomplish a precise numerical simulation of transient problem. For the time functions, the rotational speed and flow rate are indispensable.
2. Hydraulic Test
2.1. Experiment Equipment
Test pump is a centrifugal pump with small flow rate, and belongs to super-low-specific-speed range, whose impeller is open and designed with straight blades. Design parameters are as below: flow rate is 2.5 m3/h, head is 120 m, rotational speed is 2900 rpm. Hydraulic tests are carried out by closed-type test rig with B grade precision. Experimental equipments are shown in Figure 1. Power source is the variable-frequency motor, the transient flow rate is measured by LWGY type turbine flowmeter, the transient rotational speed is measured by JC1A rotational speed sensor and JW-2A microcomputer torque meter. Acquisition and disposal of test datum are accomplished by PCI-6023E data acquisition card and LabVIEW virtual instrument platform. Additionally, a KF1851 electric capacity type differential pressure transmitter is also assembled, which may be used to measure the pressure at inlet and outlet of the pump.
2.2. Results and Discussion
During shut down, centrifugal pump abruptly loses the driving power, and impeller begins to decelerate from a stable rotational speed to zero in a very short time. In this process, each parameter would change severely. Due to inertia effects, the rotational speed of impeller does not stop immediately, namely there exists a slowing process. Flow would last for a time interval, so its flow rate does not also abruptly reach zero. In short, with the deceleration of the impeller, the flow rate rapidly declines. When the stable rotational speed is 2930 rpm and the valve opening is 1.44 times rated flow rate, the experimental result is shown in Figure 2.
Result shows that the rotational speed, head, and flow rate rapidly decline with the time during shut down. At the beginning of shut down, three parameters fast decline, and then the speed rate of decrease becomes slow. The
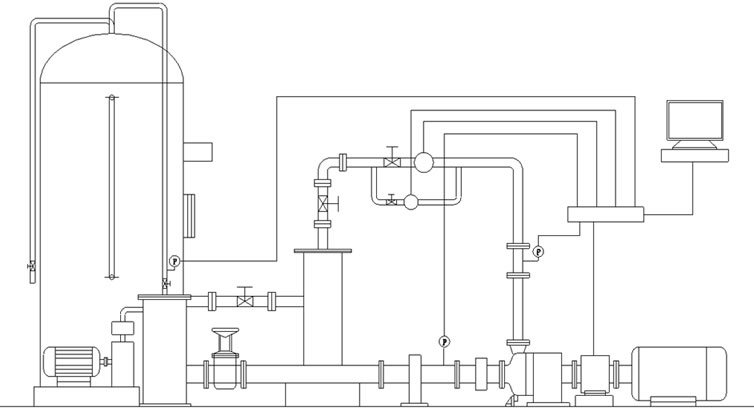
Figure 1. Test rig of external performance.
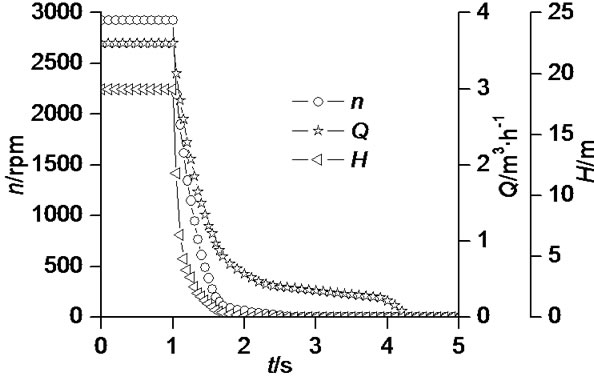
Figure 2. Variations of external performance during shutting down.
attenuation curves present the characteristics of polynomial function. It takes about 0.6 s to accomplish 93% decelerating in the rotational speed. Similarly about 1 s to accomplish 84% decline in the flow rate and 99% decline in the head. For the flow rate and head, it takes about 0.6 s to accomplish 73% and 96%, respectively. The flow rate evidently lags behind the decline process of the rotational speed, while the rotational speed also lags behind that of the head. When the rotational speed declines to zero, the inertia effect would keep fluid flowing, so the flow rate lags behind the rotational speed. The stopping time in head, rotational speed and flow rate are 1.0 s, 2.1 s and 3.3 s, respectively. The following reasons may explain above results: the characteristic of driving power mainly determines decelerating process of the rotational speed. The higher rotational speed, the more surplus energy, so the time spent during shut down would be longer. Besides pump, the decline process of flow rate is closely relates to the piping system, more resistance, less time.
3. Theoretical Calculation of Transient Head
3.1. Generalized Equation
According to the theorem of moment of momentum, the universal equation of centrifugal pump is as below [9].
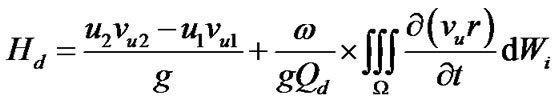 (1)
(1)
The first item in Equation (1) is Euler equation at stable state. The second item is the additional head during transient operation, which would bring transient behavior. In any transient process, angular velocity and flow rate only relate to time, while not relate to coordinate. Therefore
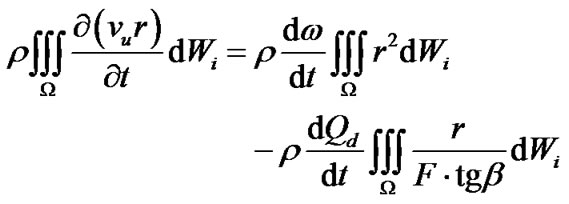 (2)
(2)
where
 (3)
(3)
where D is the nominal diameter of impeller. In centrifugal impeller, D = D2. The rotational inertia coefficient and the flow inertia coefficient of fluid in impeller are respectively as below.
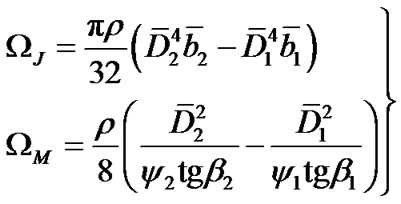 (4)
(4)
where the meaning of each parameter in (4) can be seen in Ref. [9]. The additional heads of centrifugal pump during transient operating periods are as below.
 (5)
(5)
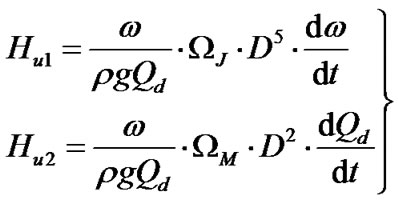 (6)
(6)
where the former in (6) is the additional head brought by the varying rotational speed, the later is another additional head brought by the varying flow rate.
3.2. Transient Head
In this paper, main geometry parameters of centrifugal impeller are shown in Table 1.
According to the experimental results, geometry value in Table 1, and transient theory head Equation (6), the flow inertia coefficient of fluid in impeller can be written.
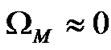 (7)
(7)
The result shows that transient behavior of centrifugal pump with straight blades mainly comes from the rotation deceleration of impeller and has little to do with the fluid deceleration. Figures 3 and 4 show the theoretical results.
It is seen that the additional theoretical head is of a clear negative impulse phenomena. The influence of the rotation acceleration of impeller (actually a negative value) on theory head is very evident. In this process, the influence of the fluid deceleration on theory head is negligible. Due to declining flow rate, the passing relative velocity in impeller channel is also low. Rotational speed declines faster and the fluid inertia generates a large area backflow region, which causes plenty of hydraulic loss and makes head decline quickly. The decline process of
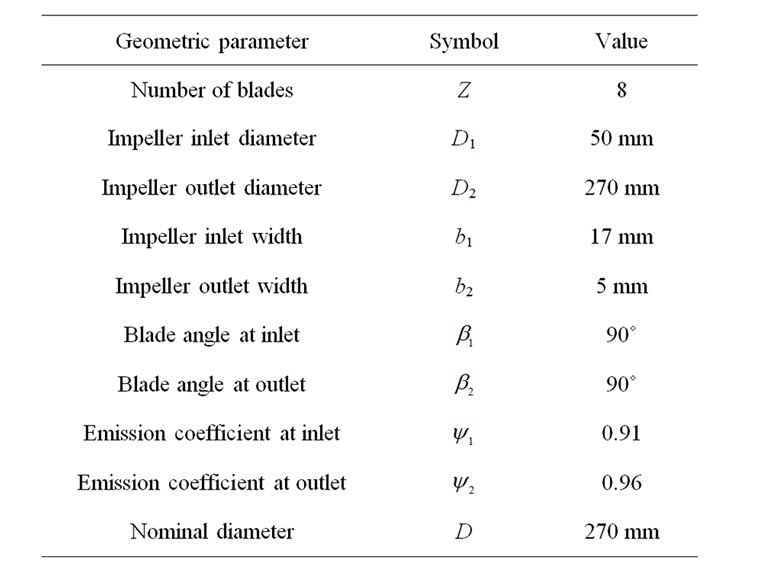
Table 1. Main geometric paramter of impeller.
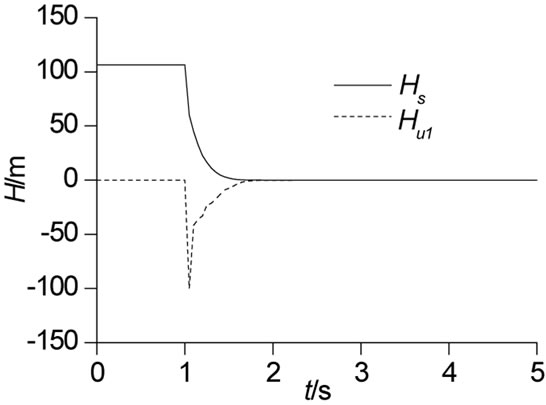
Figure 3. Transient heads during shut down.
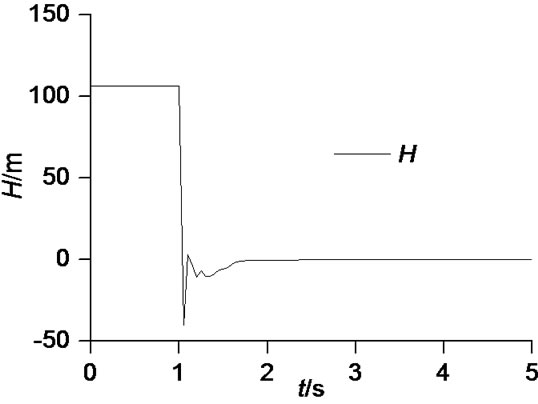
Figure 4. Total theoretical head during shut down.
static theory head is nearly consistent with that of rotational speed. The decrease head brought by the rotation deceleration mainly comes from initial stage of impeller decelerating, which is likely to relate to too high negative acceleration.
4. Numerical Simulation
4.1. Solving Control
To successfully solve the transient flow during shutting down, the flow domain is divided into two region: dynamic and stationary. The governing equation in the dynamic region are described in the arbitrary Lagrangian and Eulerian way (or the dynamic mesh conservation equations described in the FLUENT User’s Guide), whereas the stationary region is governed by ordinary N-S equation. Different regions are separately discretized, so the non-conformal meshes between two regions are linked by a pair of mesh interfaces described in the FLUENT User’s Guide. The sliding mesh technique is used to accomplish data exchange between rotor and stator.
For the flow in the dynamic region, the integral form of the dynamic mesh conservation equations for space, mass, and momentum in an arbitrary control volume V bounded by a closed surface S can be written as
 (8)
(8)
where Q is the conservation variable, F is the convective flux, D is the diffusion term, and Su is the source term of the momentum. They are given in the following expressions:
 (9)
(9)
where ρ is the fluid density, u is the fluid velocity, ub is the boundary velocity of the moving mesh, μ is the dynamic viscosity of the fluid, and p is the pressure of the fluid.
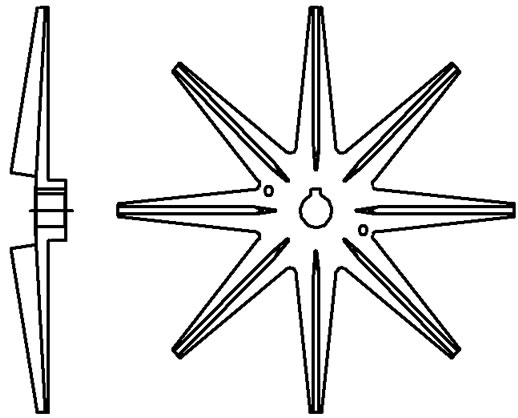
Unsteady flow is calculated by means of CFD software—FLUENT that based on a finite volume method, Yakhoth and Orzag put forward RNG 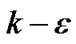 turbulence model in 1986, it is well suited to interior flow of pumps and well disposed for flows of high strain rate and high curve degree. In calculation region, multi-block mesh technology and local mesh refinement technology are used to acquire flow detail, and the total number of grids is 760,000. As is well known, the grid number is not enough for study the some micro flow like in the boundary layer, but is enough for predict the external performance and the basic flow characteristics. Open impeller and pump are shown in Figure 5. Time discretization of transient term adopts one order implicit scheme, space discretization of convection term and diffusion term adopts two order upwind scheme and central difference scheme with second order accuracy, space discretization of source term adopts standard scheme (linearization). The coupling between pressure and speed is accomplished by SIMPLE algorithm in simulations. The con-
turbulence model in 1986, it is well suited to interior flow of pumps and well disposed for flows of high strain rate and high curve degree. In calculation region, multi-block mesh technology and local mesh refinement technology are used to acquire flow detail, and the total number of grids is 760,000. As is well known, the grid number is not enough for study the some micro flow like in the boundary layer, but is enough for predict the external performance and the basic flow characteristics. Open impeller and pump are shown in Figure 5. Time discretization of transient term adopts one order implicit scheme, space discretization of convection term and diffusion term adopts two order upwind scheme and central difference scheme with second order accuracy, space discretization of source term adopts standard scheme (linearization). The coupling between pressure and speed is accomplished by SIMPLE algorithm in simulations. The con-
 (a)
(a)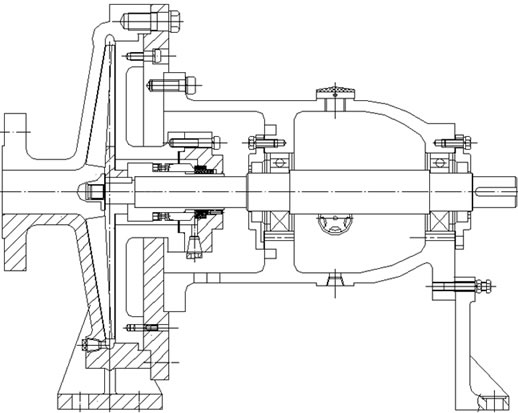 (b)
(b)
Figure 5. Pump model with open impeller. (a) Open impeller; (b) Pump sketch.
vergence criterion is 0.0001. The time step is set to 0.0001 s.
4.2. Boundary Condition
In this paper, time functions of the rotational speed and flow rate would be fit as the boundary condition of numerical simulation. To accomplish precise fitting of the test datum, the sectional fitting is applied.
1) Rotational speed. Time histories of rotational speed are fit by exponential function.
 (10)
(10)
2) Inlet condition. Time histories of flow rate are fit by polynomial function.
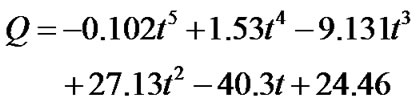 (11)
(11)
3) Outlet condition. The assumption is that flow is fully developed, namely each parameter does not change along flow direction. Outflow condition is applied.
4) Wall condition: no slip boundary condition and standard wall function are adopted at wall.
4.3. Results and Analysis
Definition of static pressure coefficient is as below.
 (12)
(12)
and
 (13)
(13)
therefore
 (14)
(14)
where p is static pressure, ρ is media density. Figure 6 is the distribution of static pressure coefficient on middle section of hub during shut down. Static pressure coefficients gradually decrease from working surface to back surface, while regularly increase from inlet to outlet. Action force and centrifugal force formed by pressure difference between working and back surface are consistent with the rotational direction of centrifugal pump, which completely accords with reality of centrifugal pump. Rotor-stator interaction makes the distribution of static pressure coefficient in channel vary obviously. Static pressure coefficient initially increases to a maximum at 0.5 s, before decreasing. At 1.2 s, static pressure coefficient begins to decrease and present regular character again. But volute tongue makes flow field present unsymmetrical structure. When time is 2 s, the rotational speed is very low, nearly reaches zero. Except for volute tongue region, distribution of static pressure coefficient is uniform.
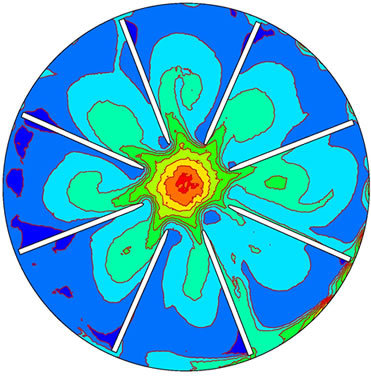
Figure 7 is the distribution of turbulence intensity during shut down. Turbulence intensity is defined as a ratio of root mean square of fluctuation velocity to mean velocity. Its temporal and spatial distributions reflect conversion process of fluctuation velocity during shut down. During shut down, high turbulence intensity converts to low turbulence intensity, i.e., high Reynolds number (may reach to millions) converts low Reynolds number and till zero. Hence the turbulence mode would develop and change.
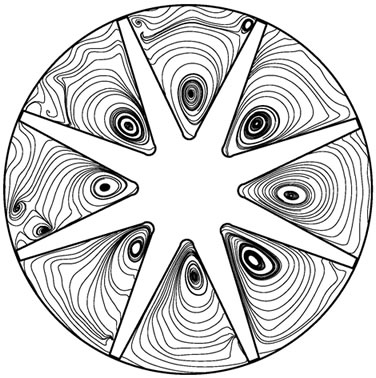
Figure 8 is the streamline on middle section of hub during shut down. At the beginning of startup, no backflow appears, then large area axial eddies appear and the rotational direction is reversed. When time is 2 s, rotational speed is very low and close to zero, but flow rate is still relatively high and backflow region still exists. Meanwhile, backflow region severely decreases and center of every axial eddy close to rotation center. Rotational speed has reached to zero after 3 s, then the flow around vanes leads to a backflow in channel. The Rossby dimensionless number could reflect the influence of vane curvature and rotation on backflow in the impeller.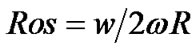 , this formula shows the ratio of inertial force (centrifugal force) to Coriolis force. Where curva-
, this formula shows the ratio of inertial force (centrifugal force) to Coriolis force. Where curva-
 (a)
(a)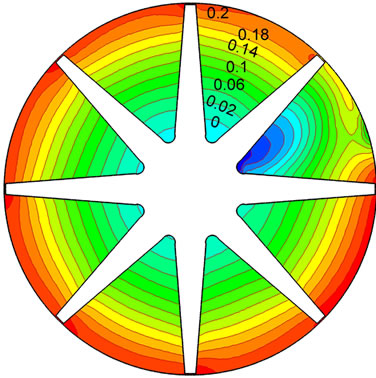 (b)
(b)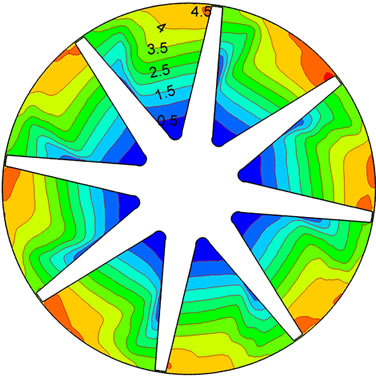 (c)
(c) (d)
(d)
Figure 6. Distribution of static pressure coefficient during shutting down. (a) 0.1 s; (b) 0.5 s; (c) 1.2 s; (d) 2.0 s.
 (a)
(a)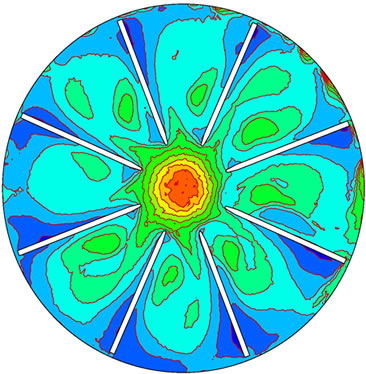 (b)
(b)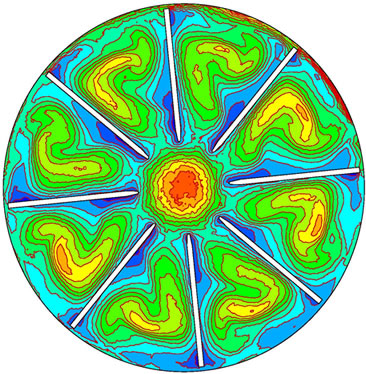 (c)
(c)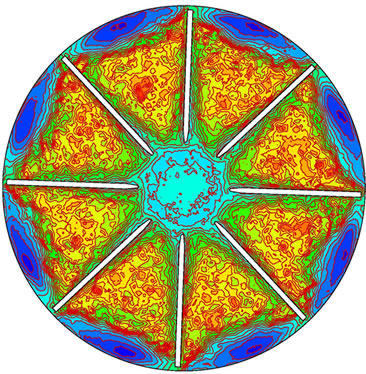 (d)
(d)
Figure 7. Variation of turbulence intensity during shut down. (a) 0.1 s; (b) 1.2 s; (c) 2.0 s; (d) 3.0 s.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 8. Variation of streamline during shutting down. (a) 0.1 s; (b) 1.2 s; (c )2.0 s; (d) 3.0 s.
ture brings inertial force and rotation brings Coriolis force. For flow rates laging behind rotational speed, the Rossby number gradually increases during shut down. In Rossby number, the circular velocity is far lower than its relative velocity. Except above reason, valve type and annular volute may are another two important reasons in this paper.
5. Conclusion
Transient behavior of a low-specific-speed centrifugal pump with an open impeller and straight blades during shut down is researched. Experimental result approves that the decline of the flow rate evidently lags behind that of the rotational speed, which in turn lags behind that of the head, and three parameters decline rapidly initially before slowing. Theoretical analysis shows that transient theory head is of a clear negative-impulsion phenomena. Transient effect of centrifugal pump with straight blades mainly comes from the rotational acceleration of impeller, while the fluid acceleration is negligible. During shut down, the Rossby dimensionless number gradually increases. Flow inertia makes a large area backflow appear when the rotational speed approaches zero. Transformation trend of the flow field in numerical simulation reflects real flow characters of shut down, which are consistent with interior flow theory of centrifugal pumps.
6. Acknowledgements
This study is supported by the National Natural Science Foundation of China (No. 21076198, 51276172) and the National Basic Research Program (“973” Program, No. 2009CB724303).
REFERENCES
- H. Tsukamoto and H. Ohashi, “Transient Characteristics of a Centrifugal Pump during Starting Period,” ASME Journal of Fluids Engineering, Vol. 104, No. 1, 1982, pp. 6-13. doi:10.1115/1.3240859
- P. J. Lefebvre and W. P. Barker, “Centrifugal Pump Performance during Transient Operation,” ASME Journal of Fluids Engineering, Vol. 117, No. 1, 1995, pp. 123-128. doi:10.1115/1.2816801
- K. Farhadi, A. Bousbia-salah and F. D’Auria, “A Model for the Analysis of Pump Start-Up Transients in Tehran Research Reactor,” Progress in Nuclear Energy, Vol. 49, No. 7, 2007, pp. 499-510. doi:10.1016/j.pnucene.2007.07.006
- P. Thanapandi and R. Prasad, “Centrifugal Pump Transient Characteristics and Analysis Using the Method of Characteristics,” International Journal of Mechanical Sciences, Vol. 37, No. 1, 1995, pp. 77-89. doi:10.1016/0020-7403(95)93054-A
- A. Dazin, G. Caignaert and G. Bois, “Transient Behavior of Turbomachineries: Applications to Radial Flow Pump Startups,” ASME Journal of Fluids Engineering, Vol. 129, No. 11, 2007, pp. 1436-1444. doi:10.1115/1.2776963
- S. Duplaa, O. Coutier-Delgosha, A. Dazin, et al., “Experimental Study of a Cavitating Centrifugal Pump during Fast Startups,” ASME Journal of Fluids Engineering, Vol. 132, No. 2, 2010, Article ID: 021301.
- W. Chen, X. W. Ke, D. Z. Wu, et al., “Analysis on Transient Performance of Mixed Flow Pump During Stopping Period,” Fluid Machinery, Vol. 34, No. 12, 2006, pp. 1-4.
- H. Tsukamoto, S. Matsunaga and H. Yoneda, “Transient Characteristics of a Centrifugal Pump during Stopping Period,” ASME Journal of Fluids Engineering, Vol. 108, No. 4, 1986, pp. 392-399. doi:10.1115/1.3242594
- J. S. Chang, “Transients of Hydraulic Machine Installations,” Higher Education Press, Beijing, 2005.
NOTES
*Corresponding author.

