Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21665,6 pages DOI:10.4236/jmp.2012.38111
Propagation of Electrostatic Waves in an Ultra-Relativistic Dense Dusty Electron-Positron-Ion Plasma
Department of Physics, Jahangirnagar University, Dhaka, Bangladesh
Email: niparoybd@gmail.com, mamun_phys@yahoo.co.uk, salim.zobaer@yahoo.com
Received August 26, 2011; revised October 26, 2011; accepted January 5, 2012
Keywords: Degenerate Plasma; Ultra-Relativistic Limit; Solitary Waves; K-dV Equation; Pseudo-Potential Method
ABSTRACT
The nonlinear propagation of waves (specially solitary waves) in an ultra-relativistic degenerate dense plasma (containing ultra-relativistic degenerate electrons and positrons, cold, mobile, inertial ions, and negatively charged static dust) have been investigated by the reductive perturbation method. The linear dispersion relation and Korteweg de-Vries equation have been derived whose numerical solutions have been analyzed to identify the basic features of electrostatic solitary structures that may form in such a degenerate dense plasma. The existence of solitary structures has been also verified by employing the pseudo-potential method. The implications of our results in astrophysical compact objects have been briefly discussed.
1. Introduction
Now-a-days, a great deal of interest has been grown in understanding of the basic properties of matter under extreme conditions (occurred by significant compression of the interstellar medium) [1-6], which are found in some interstellar compact objects. One of these extreme conditions is high density of degenerate matter in these compact objects which have ceased burning thermonuclear fuel, and thereby no longer generate thermal pressure. These interstellar compact objects are contracted significantly, and as a result, the density of their interiors becomes extremely high to provide non-thermal pressure via degenerate fermions/electron-positron pressure and particle-particle interaction. These compact objects support themselves against gravitational collapse by cold, degenerate fermions/electron-positron pressure, having their interiors close to a dense solid (ion lattice surrounded by degenerate electron-positrons, and possibly other heavy particles like dust) or close to a giant atomic nucleus (a mixture of interacting nucleus and electronpositron and possibly other heavy elementary particles and condensate or dust).
The degenerate fermion number density in such a compact object is so high that it follows the equation of state for degenerate fermions mathematically explained by Chandrasekhar [3] for two limits, namely non-relativistic and ultra-relativistic limits. The degenerate electron equation of state of Chandrasekhar is 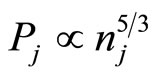 (“j” stands for electron and positron) for non-relativistic limit and
(“j” stands for electron and positron) for non-relativistic limit and  for ultra-relativistic limit, where
for ultra-relativistic limit, where  is the degenerate electron pressure and
is the degenerate electron pressure and  is the degenerate fermion number density. We note that the degenerate pressure depends only on the number density of the species, but not on their temperatures. The quantum effects on linear [7-13] and nonlinear [11,14,15] propagation of electrostatic and electromagnetic waves have been investigated by using the quantum hydrodynamic (QHD) model [13,16], which is an extension of classical fluid model in a plasma, and by using the quantum magnetohydrodynamic (QMHD) model [7,14,15], which involve spin-
is the degenerate fermion number density. We note that the degenerate pressure depends only on the number density of the species, but not on their temperatures. The quantum effects on linear [7-13] and nonlinear [11,14,15] propagation of electrostatic and electromagnetic waves have been investigated by using the quantum hydrodynamic (QHD) model [13,16], which is an extension of classical fluid model in a plasma, and by using the quantum magnetohydrodynamic (QMHD) model [7,14,15], which involve spin- and one-fluid MHD equations.
and one-fluid MHD equations.
Recently, a number of theoretical investigations have also been made of the nonlinear propagation of electrostatic waves in degenerate quantum plasma by a number of authors, e.g. Hass [17], Misra and Samanta [18], Mistra et al. [19] etc. However, these investigations are based on the electron equation of state 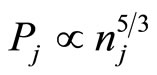 which is valid for the non-relativistic limit. To the best of our knowledge, no investigation for a dusty electron-positron plasma has been made of the nonlinear propagation of electrostatic waves based on the degenerate fermion equation of state (
which is valid for the non-relativistic limit. To the best of our knowledge, no investigation for a dusty electron-positron plasma has been made of the nonlinear propagation of electrostatic waves based on the degenerate fermion equation of state (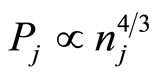 ) which is valid for ultrarelativistic limit. Therefore, in this Brief Communication, we consider a degenerate dense plasma containing cold ion fluid and ultra-relativistic degenerate electrons and positrons following the equation of state
) which is valid for ultrarelativistic limit. Therefore, in this Brief Communication, we consider a degenerate dense plasma containing cold ion fluid and ultra-relativistic degenerate electrons and positrons following the equation of state , and study the basic features of the solitary waves in such an ultra-relativistic degenerate dense plasma. The model is relevant to compact interstellar objects, particularly to white dwarfs which have almost spherical shape.
, and study the basic features of the solitary waves in such an ultra-relativistic degenerate dense plasma. The model is relevant to compact interstellar objects, particularly to white dwarfs which have almost spherical shape.
2. Governing Equations
We consider inertialess ultra-relativistic degenerate electron-positron, cold, mobile, inertial ion fluid, and negatively charged static dust in our four component plasma system. Degenerate pressure of electron-positron fluid has been expressed in terms of density by using the ultra-relativistic limit. The nonlinear dynamics of the electrostatic perturbation mode in such a dusty e-p-i plasma system is described by the following equations.
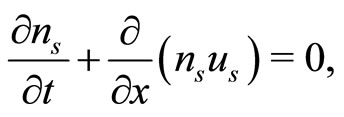 (1)
(1)
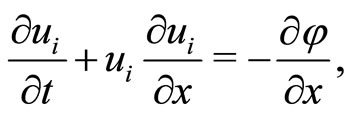 (2)
(2)
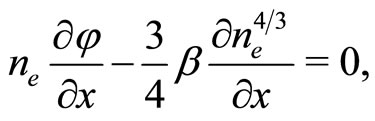 (3)
(3)
 (4)
(4)
 (5)
(5)
where  is the number density of the plasma species “s” (
is the number density of the plasma species “s” ( for electrons, positrons, and ions respectively) normalized by its equilibrium value
for electrons, positrons, and ions respectively) normalized by its equilibrium value ,
, 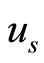 is the fluid speed (of the species s) normalized by the ion-acoustic speed
is the fluid speed (of the species s) normalized by the ion-acoustic speed ,
, 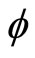 is the electrostatic wave potential normalized by (
is the electrostatic wave potential normalized by (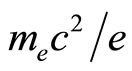 ), x is the space variable normalized by
), x is the space variable normalized by 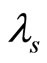
 , t is the time variable normalized by the ion plasma period
, t is the time variable normalized by the ion plasma period
 .
.
The constants  and
and 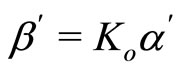 with
with
 ,
, 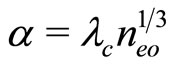 ,
,  (
(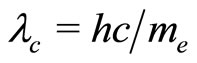 ).
).
We can express 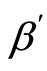 in terms of
in terms of  as
as  with
with . Here,
. Here,  ,
,  , and
, and 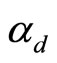 are respectively the density ratio (
are respectively the density ratio (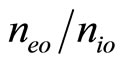 ), (
), ( ), and (
), and (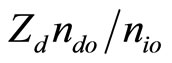 ).
).
3. Derivation of K-dV Equation
To examine electrostatic perturbations propagating in the ultra-relativistic degenerate dense plasma by analyzing the outgoing solutions of Equations (1)-(5), we first introduce the stretched coordinates [20]
 (6)
(6)
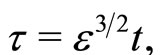 (7)
(7)
where  is the wave phase speed (
is the wave phase speed ( with
with 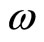 being angular frequency and
being angular frequency and  being the wave number of the perturbation mode), and
being the wave number of the perturbation mode), and 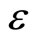 is a smallness parameter measuring the weakness of the dispersion (
is a smallness parameter measuring the weakness of the dispersion (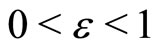 ). We then expand
). We then expand ,
,  ,
, 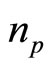 ,
, 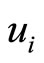 , and
, and , in power series of
, in power series of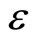 :
:
 (8)
(8)
 (9)
(9)
 (10)
(10)
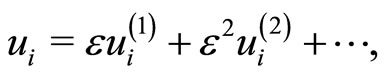 (11)
(11)
 (12)
(12)
and develop equations in various powers of . To the lowest order in
. To the lowest order in , Equations (1)-(12) give
, Equations (1)-(12) give
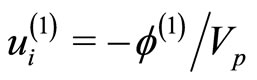 ,
, 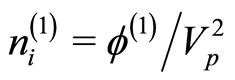 ,
,  ,
,
 , and
, and .
.
We are interested in studying the nonlinear propagation of these dispersive dust ion-acoustic type electrostatic waves in a degenerate plasma. To the next higher order in , we obtain a set of equations
, we obtain a set of equations
 (13)
(13)
 (14)
(14)
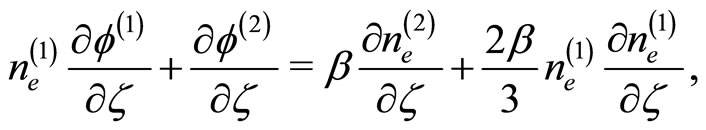 (15)
(15)
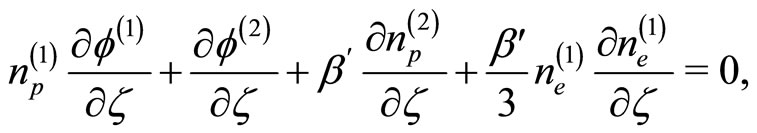 (16)
(16)
 (17)
(17)
Now, combining Equations (13)-(17) we deduce a modified Korteweg-de Vries equation
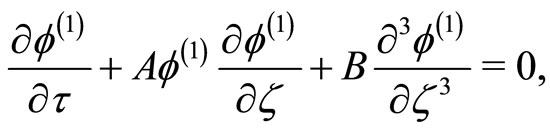 (18)
(18)
where
 (19)
(19)
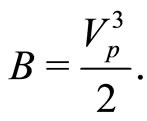 (20)
(20)
For a moving frame moving with a speed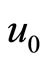 , the stationary solitary wave solution of Equation (18) is
, the stationary solitary wave solution of Equation (18) is
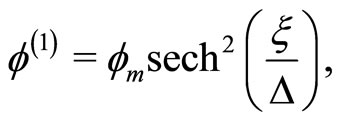 (21)
(21)
where the special stretched coordinates, 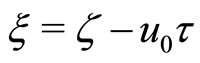 , the potential,
, the potential,  , and the width,
, and the width,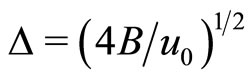 .
.
4. Numerical Analysis
It is obvious from Equation (19) and Equation (21) that the degenerate plasma under consideration supports compressive electrostatic solitary waves which are associated with a positive potential. It is observed from Equations (19)-(21) that the amplitude (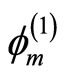 ) of these solitary structures is directly proportional to square root of
) of these solitary structures is directly proportional to square root of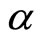 , i.e. proportional to
, i.e. proportional to 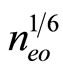 and their width (
and their width ( ) is directly proportional to
) is directly proportional to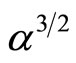 , i.e. to the square root of
, i.e. to the square root of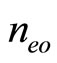 . It is also seen that the amplitude (width) increases (decreases) with the speed
. It is also seen that the amplitude (width) increases (decreases) with the speed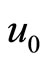 . The electrostatic solitary profiles are shown in Figures 1 and 2. The compressive dust ionacoustic solitary wave (DIASW), which can be treated as positive DIASW in a dusty e-p-i plasma system, is theoretically investigated.
. The electrostatic solitary profiles are shown in Figures 1 and 2. The compressive dust ionacoustic solitary wave (DIASW), which can be treated as positive DIASW in a dusty e-p-i plasma system, is theoretically investigated.

Figure 1. The solitary profile represented by Equation (21) with u0 = 0.1 showing the effect of α.
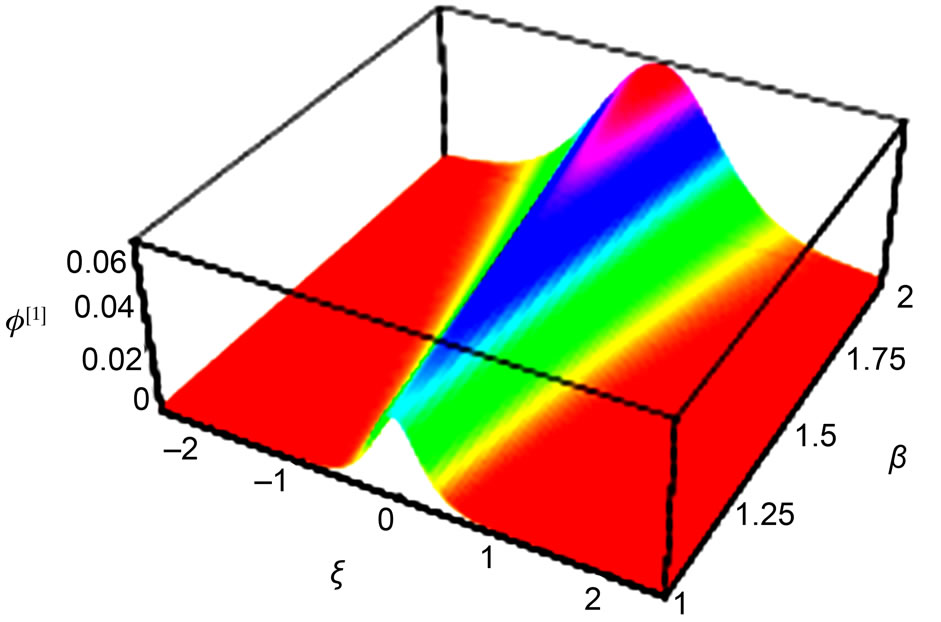
Figure 2. Showing the effect of β on the solitary profiles represented by Equation (21) with u0 = 0.1.
5. Derivation of Energy Integral
The existence of DIASWs can be verified by using pseudo potential approach.To do so we first make all independent variables depend on a single variable  by the transformation
by the transformation  (where
(where 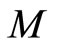 is the Mach number, solitary wave speed/
is the Mach number, solitary wave speed/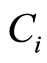 ). This transformation allows the steady state condition (
). This transformation allows the steady state condition ( ), and the appropriate boundary conditions for localized perturbation (viz.
), and the appropriate boundary conditions for localized perturbation (viz.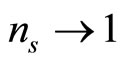 ,
, 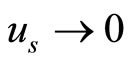 , and
, and  at
at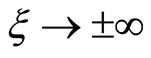 ) allow us to write Equations (1)-(5) as
) allow us to write Equations (1)-(5) as
 (22)
(22)
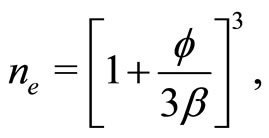 (23)
(23)
 (24)
(24)
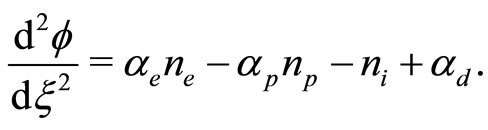 (25)
(25)
Now, substituting Equations (22)-(24) into Equation (25), multiplying the resulting equation by  and applying the boundary condition,
and applying the boundary condition,  at
at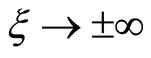 , we obtain
, we obtain
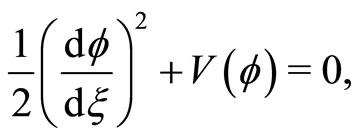 (26)
(26)
where  is given by
is given by
 (27)
(27)
in which  is the integration constant chosen in such a way that
is the integration constant chosen in such a way that 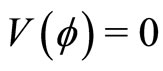 at
at . Equation (26) can be regarded as an “energy integral” [21,22] of an oscillating particle of unit mass, with pseudo-speed
. Equation (26) can be regarded as an “energy integral” [21,22] of an oscillating particle of unit mass, with pseudo-speed , pseudo-position
, pseudo-position , pseudotime
, pseudotime , and pseudo-potential
, and pseudo-potential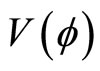 . This equation is valid for DIASWs in a dusty e-p-i plasma.
. This equation is valid for DIASWs in a dusty e-p-i plasma.
6. Numerical Analysis
The expansion of  around
around 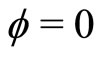 is
is
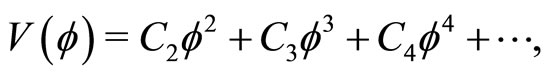 (28)
(28)
where ,
, 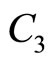 , and
, and  are given by
are given by
 (29)
(29)
 (30)
(30)
 (31)
(31)
with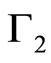 ,
,  , and
, and  are expressed as
are expressed as
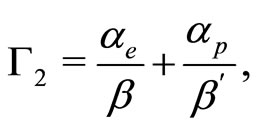 (32)
(32)
 (33)
(33)
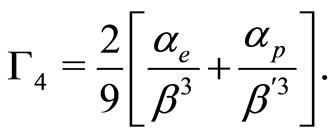 (34)
(34)
We now analyze Equations (27) and (28) with the help of Equations (29)-(31), and investigate the basic properties of SWs in a dusty e-p-i plasma. To study the possibility for the formation of the SWs, as well as their basic features (if they are formed), we first discuss the general conditions for the existence of the SWs. These conditions are
1)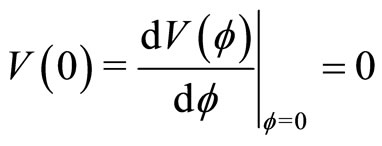 , which are already satisfied by the equilibrium charge neutrality condition, and by the boundary condition chosen to obtain the value of the integration constant (
, which are already satisfied by the equilibrium charge neutrality condition, and by the boundary condition chosen to obtain the value of the integration constant (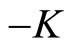 ).
).
2) , which will be satisfied if
, which will be satisfied if
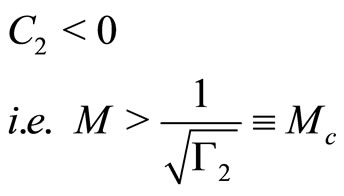 (35)
(35)
where  is the critical Mach number.
is the critical Mach number.
3) , which will be satisfied if
, which will be satisfied if
 (36)
(36)
where  is the amplitude of SWs.
is the amplitude of SWs.
4)  for positive SWs (by positive SWs we mean compressive SWs, i.e. SWs with positive potential),
for positive SWs (by positive SWs we mean compressive SWs, i.e. SWs with positive potential), 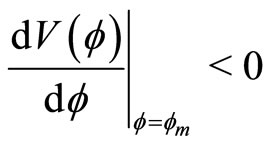 for negative SWs (by negative SWs we mean rarefactive SWs, i.e. SWs with negative potential), and for DLs
for negative SWs (by negative SWs we mean rarefactive SWs, i.e. SWs with negative potential), and for DLs
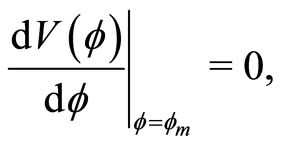 (37)
(37)
which will be satisfied if
 (38)
(38)
Conditions 1)-3) must be satisfied for SWs. However, in addition of these three, the first (second) of 4) is required only for positive (negative) SWs. Therefore, the minimum (critical) value of M for existence of SWs is determined by Equation (35). Hence the final condition reduces to
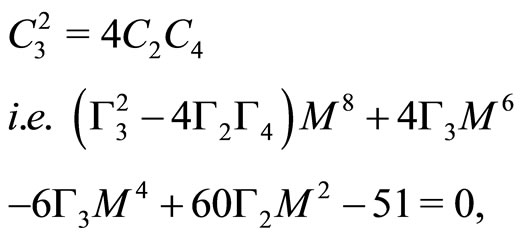 (39)
(39)
Now, using Equations (36) and (38), one can finally obtain
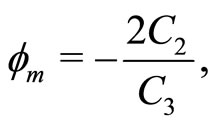 (40)
(40)
It is obvious from condition 2) that . Therefore, polarity of the nonlinear potential structures (SWs) depend on the polarity of
. Therefore, polarity of the nonlinear potential structures (SWs) depend on the polarity of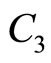 . Thus,
. Thus,  will give the boundaries separating the parametric regimes for the positive and negative SWs.
will give the boundaries separating the parametric regimes for the positive and negative SWs.
The solutions of Equation (39) for low speed DIA waves is plotted for  and
and 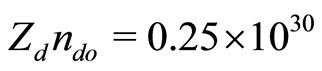 (in Figure 3). It is observed that when
(in Figure 3). It is observed that when  and M exceeds
and M exceeds  (from
(from  to
to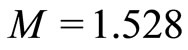 ), the existence of DIASWs can be verified. It can be said that conditions 1)-3) has been satisfied for DIASWs. However, in addition of these three, the first (second) of 4) is satisfied for positive (negative) SWs. In other words, any point above the solid curve (
), the existence of DIASWs can be verified. It can be said that conditions 1)-3) has been satisfied for DIASWs. However, in addition of these three, the first (second) of 4) is satisfied for positive (negative) SWs. In other words, any point above the solid curve ( ) corresponds to the existence of DIASWs; and any point above (below) the dashed (
) corresponds to the existence of DIASWs; and any point above (below) the dashed (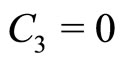 ) curve corresponds to the existence of the negative (positive) SWs. The number densities have been chosen randomly to obtain SWs from the standard value [23]. It has been observed from Figure 4 that both positive and negative solitary waves coexist. Figure 4 also shows the formation of solitary waves everywhere except the boundary condition,
) curve corresponds to the existence of the negative (positive) SWs. The number densities have been chosen randomly to obtain SWs from the standard value [23]. It has been observed from Figure 4 that both positive and negative solitary waves coexist. Figure 4 also shows the formation of solitary waves everywhere except the boundary condition, 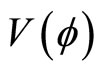 around
around .
.
7. Discussion
The solitary profile from the solution of K-dV equation includes compressive SWs, i.e. SWs with positive potential (shown in Figure 1). It is the exact solitary profile created due to the balance between the nonlinearity and dispersion. But negative SWs (by negative SWs we mean rarefactive SWs, i.e. SWs with negative potential) can occur in seldom. So it is obvious that we need a method which supports the propagation of both positive and negative SWs. Hence the pseudo-potential method is introduced. The small amplitude limit of the pseudopotential (obtained from the derivation of the energy integral) shows the coexistence of both positive and negative DIASWs (shown in Figure 4). For both positive and negative DIASWs, the number density of plasma particles has an important role. The potential of the waves depends on α, as well as β, which implies that an extremely large number density of plasma particles supports the non-linear wave profiles like solitary waves.
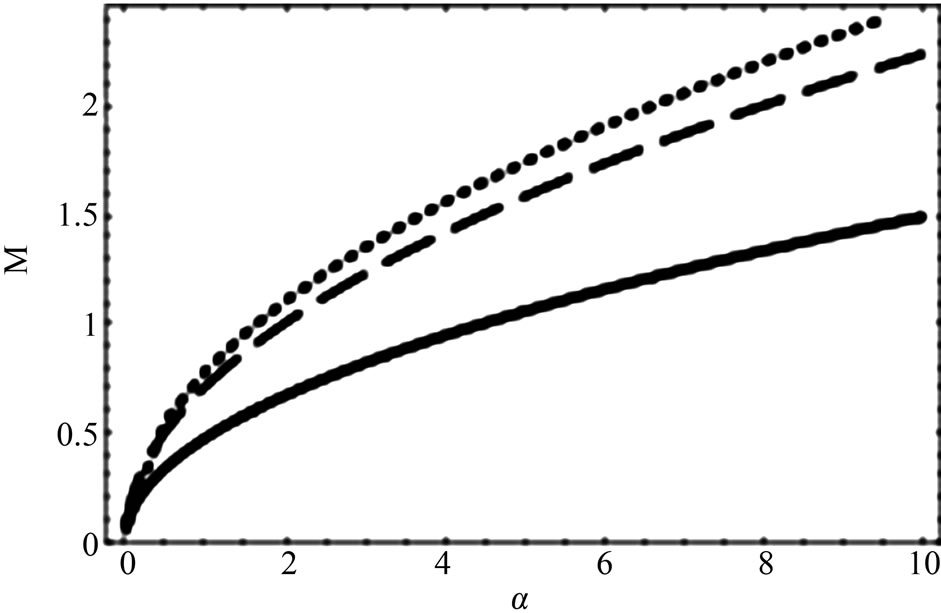
Figure 3. Showing how M varies with α as well as β for different conditions. The solid line represents the C2 = 0 curve, the dotted line represents the solutions of Equation (39) for low speed DIA waves, and the dashed line represents the C3 = 0 curve (for nio = 3.95 × 1030).
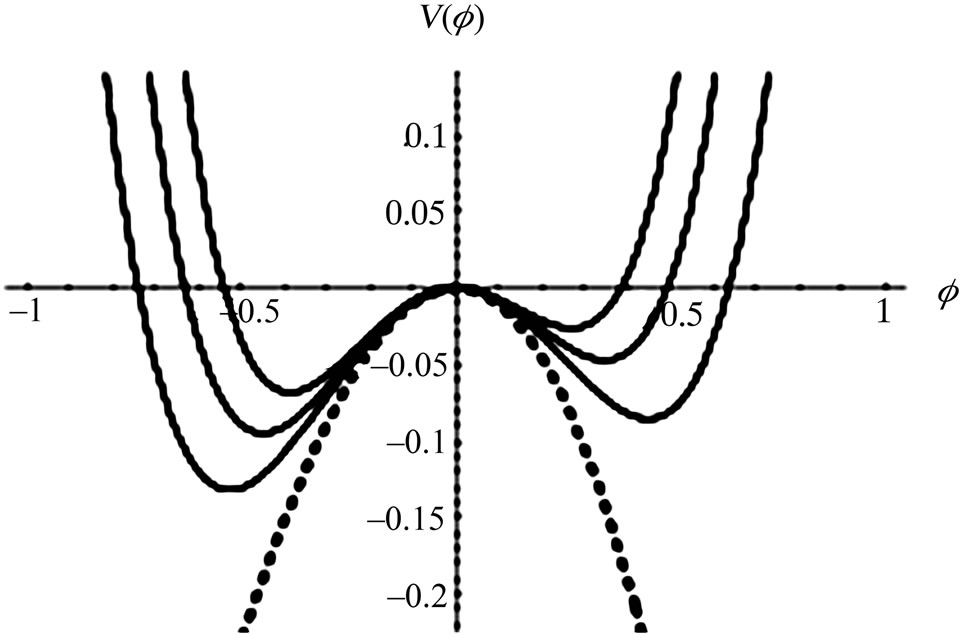
Figure 4. Showing the existence of SWs when α = 4.3 and M exceeds Mc (specifically, M = 0.636, M = 1.104, and M = 1.528), and the dashed line shows V(f) curve around f = 0.
To summarize, we have investigated electrostatic solitary waves in an ultra-relativistic degenerate dense plasma, which is relevant to interstellar spherical compact objects like white dwarfs. The degenerate dense plasma is found to support both positive and negative solitary structures whose basic features (amplitude, width, speed, etc.) depend only on the plasma number density. It has been shown here that the amplitude, width, and speed increase with the increase of the plasma number density, but the electrostatic potential is negative. We finally hope that our present investigation will be useful for understanding the basic features of the localized electrostatic disturbances in an ultra-relativistic ultra-cold degenerate dense dusty plasma which is found in some astrophysical objects, (e.g. white dwarf stars, neutron stars, etc.) Thus the model we have considered in our present investigation (a dusty e-p-i plasma) supports the nonlinear propagation of dust-ion-acoustic solitary waves in extreme conditions for ultra-relativistic limit of density of plasma particles, which are found in many interstellar compact objects.
8. Acknowledgements
The Third World Academy of Science (TWAS) Research Grant for the research equipment are gratefully acknowledged (by M. S. Zobaer and A. A. Mamun).
REFERENCES
- S. Chandrasekhar, “The Density of White Dwarf Stars,” Philosophical Magazine, Vol. 11, No. 7, 1931, pp. 592- 596.
- S. Chandrasekhar, “The Maximum Mass of Ideal White Dwarfs,” Astrophysical Journal, Vol. 74, No. 1, 1931, pp. 81-82. doi:10.1086/143324
- S. Chandrasekhar, “The Highly Collapsed Configurations of a Steller Mass (Second Paper),” Monthly Notics of the Royal Astronmical Science, Vol. 170, No. 1935, 1935, pp. 226-228.
- D. Koester and G. Chanmugam, “Physics of White Dwarf Stars,” Report on Progress in Physics, Vol. 53, No. 7, 1990, p. 837. doi:10.1088/0034-4885/53/7/001
- S. L. Shapiro and S. A. Teukolsky, “Black holes, White dwarfs, and neutron Stars: The Physics of Compact - bjects,” John Wiley and Sons, New York, 1983.
- E. Garcia-Berro, S. Torres, L. G. Althaus, I. Renedo, P. Lorén-Aguiltar, A. H. Córsico R. D. Rohrmann, M. Salaris, and J. Isern, “A White Dwarf Cooling Age of 8 Gyr for NGC 6791 from Physical Separation Process,” Nature, Vol. 465, 2010, pp. 194-196. doi:10.1038/nature09045
- G. Brodin and M. Marklund, “Spin Megnetohydrodynamics,” New Journal of Physics, Vol. 9, No. 8, 2007, pp. 227. doi:10.1088/1367-2630/9/8/277
- P. K. Shukla and B. Eliasson, “Formation and Dynamics of Dark Solitons and Vortices in Quantum ElectrPlasmas,” Physics Review Letter, Vol. 96, No. 24, 2006, Article ID: 245001. doi:10.1103/PhysRevLett.96.245001
- P. K. Shukla and B. Eliasson, “Nonlinear Interactions between Electromagnetic Waves and Electron Plasma Oscillations in Quantum Plasmas,” Physics Review Letter, Vol. 99, No. 9, 2007, Article ID: 096401. doi:10.1103/PhysRevLett.99.096401
- D. Shaikh and P. K.Shukla, “Fluid Turbulance in quantum Plasmas,” Physics Review Letter, Vol. 99, No. 12, 2007, Article ID: 125002. doi:10.1103/PhysRevLett.99.125002
- M. Marklund and G. Brodin, “Dynamics of Spin-1/2 Quantum Plasmas,” Physics Review Letter, Vol. 98, No. 2, 2007, Article ID: 025001. doi:10.1103/PhysRevLett.98.025001
- P. K. Shukla, “A New Spin in Quantum Plasmas,” Nature Physics, Vol. 5, 2009, pp. 92-93. doi:10.1038/nphys1194
- W. Masood, B. Eiasson and P. K. Shukla, “Electromagnetic Wave Equations for Relativistically Degenerate Quantum Magnetoplasmas,” Physics Review E, Vol. 81, No. 6, 2010, Article ID: 066401. doi:10.1103/PhysRevE.81.066401
- G. Brodin and M. Marklund, “Spin Solitons in Magneized Pair Plasmas, Physics of Plasmas, Vol. 14, No. 11, 2007, Article ID: 112107. doi:10.1063/1.2793744
- M. Marklund, B. Eiasson and P. K. Shukla, “Magnetosonic Solitons in a Fermionic Quantum Plasma,” Physics Review E, Vol. 76, No. 6, 2007, Article ID: 067401. doi:10.1103/PhysRevE.76.067401
- G. Manfredi, “How to Model Quantum Plasmas,” Proceedings of the Workshop on Kinetic Theory The Fields Institute Communications Series, Toronto, 29 March-2 April 2004, p. 263.
- F. Hass, “Variational Approach for the Quantum Zakharov System,” Physics of Plasmas, Vol. 14, No. 4, 2007, Article ID: 042309. doi:10.1063/1.2722271
- A. Misra and S. Samanta, “Quantum Electro Acoustic Double Layers in a Magnetoplasma,” Physics of Plasmas, Vol. 15, No. 12, 2008, Article ID: 122307. doi:10.1063/1.3040014
- A. P. Misra, S. Banerjee, F. Haas, P. K. Shukla and L. PG. Assis, “Temporal Dynamics in Quantum Zakharov Equations for Plasmas,” Physics of Plasmas, Vol. 17, No. 3, 2010, Article ID: 032307. doi:10.1063/1.3356059
- S. Maxon and J. Viecelli, “Spherical Solitons,” Physics Review Letter, Vol. 32, No. 1, 1974, pp. 4-6. doi:10.1103/PhysRevLett.32.4
- I. B. Bernstein, J. M. Greene and M. D. Kruskal, “Exact Nonlinear Plasma Oscillations,” Physics Review Letter, Vol. 108, No. 3, 1957, p. 546.
- R. Z. Sagdeev, “Cooperative Phenomena and Shock Waves in Collisionless Plasmas,” Reviews of Plasma Physics, Vol. 4, 1966, p. 23
- A. A. Mamun and P. K. Shukla, “Arbitrary amplitude solitary waves and double layers in an Ultra-Relativistic Degenerate Dense Dusty Plasma,” Physics Letter A, Vol. 374, No. 41, 2010, pp. 4238-4241. doi:10.1016/j.physleta.2010.08.038

