Theoretical Economics Letters
Vol.06 No.03(2016), Article ID:67377,10 pages
10.4236/tel.2016.63060
A Geometric Approach to Temptation and Self-Control
Koji Abe
Graduate School of Business Administration, Kobe University, Kobe, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 4 April 2016; accepted 12 June 2016; published 15 June 2016
ABSTRACT
By making use of a geometry of preferences, Abe (2012) proves the Gul and Pesendorfer’s utility representation theorem about temptation without self-control. This companion paper provides a similar proof for the Gul and Pesendorfer's utility representation theorem about temptation and costly self-control. As a result, the both theorems are proved in the unified way.
Keywords:
Temptation, Self-Control, Utility Representation, Geometric Approach

1. Introduction
There is a large and growing literature on temptation and self-control in economics [1] [2] . Gul and Pesendorfer [3] propose basic models of choice under temptation and provide preference foundations for the models. We provide an alternative proof of the main theorem in [3] , that is, the Gul and Pesendorfer’s utility representation theorem about temptation and costly self-control. The proof makes use of a geometry of preferences and goes as follows. We first extract behaviors that display temptation and self-control. We then characterize the intuitive notions of temptation and self-control geometrically. Finally, we prove the utility representation theorem using the characterization. The proof highlights the reason why the self-control part can be written by sum of commitment utility and temptation utility. The proof also provides the refined testable implications of the Gul and Pesendorfer model.
This geometric approach is taken by the companion paper, [4] , to prove the Gul and Pesendorfer’s utility representation theorem about temptation without self-control. As a result, we prove the two representation theorems by an intuitive and unified approach.
This paper is organized as follows. Section 2 summarizes the Gul and Pesendorfer’s utility representation theorem. In Section 3, we explore our notions of temptation and self-control and derive those cone representations. Section 4 proves the Gul and Pesendorfer’s representation theorem using the result of Section 3. In Section 5, we discuss relation between our approach and the Gul and Pesendorfer’s approach.
2. The Gul and Pesendorfer Theorem
Let Z be a compact metric space of prizes. Let ∆ be the set of all Borel probability measures over Z and be endowed with the topology of weak convergence. Let 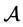 be the set of all compact (with respect to the topology of weak convergence) subsets of ∆ and be endowed with the topology induced by the Hausdorff metric. For any
be the set of all compact (with respect to the topology of weak convergence) subsets of ∆ and be endowed with the topology induced by the Hausdorff metric. For any 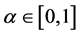 and
and , we let
, we let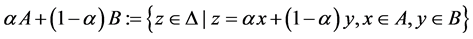 . A typical element A of
. A typical element A of 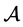 is called a menu (of lotteries).
is called a menu (of lotteries).
Let 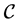 be the set of continuous affine mappings from ∆ to real numbers; that is,
be the set of continuous affine mappings from ∆ to real numbers; that is, 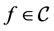 if and only if f is continuous on ∆ and satisfies
if and only if f is continuous on ∆ and satisfies 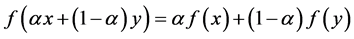 for all
for all 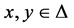 and for all
and for all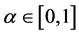 . Throughout this paper, we say that f is cardinally equivalent to a function g when
. Throughout this paper, we say that f is cardinally equivalent to a function g when 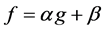 for some positive
for some positive 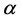 and real
and real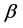 .
.
We call the following model of utility function the Gul and Pesendorfer model.
Definition 1. A utility function U on menus is said to be a Gul and Pesendorfer model if it is a function of the form:
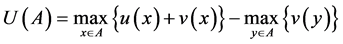 (1)
(1)
for some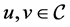 .
.
Gul and Pesendorfer [3] provided preference foundations for this model. Let 


upper semi-continuous if the sets 
lower semi-continuous if the sets 
continuous if it is upper and lower semi-continuous.
We consider the following axioms.
Axiom 1 (Preference). 
Axiom 2 (Continuity). 
Axiom 3 (Independence). 


Axiom 4 (Set Betweenness). 

Axiom 1 is a standard revealed preference axiom. Axioms 2 and 3 are variants of the von Neumann and Morgenstern axioms adapted to the preferences-over-menus setting. Axioms 4 is viewed as intuitive notion of costly self-control behaviors under temptation as we explain below.
Imagine a situation in which an individual first chooses a menu and then selects an alternative from that menu. Suppose that the individual evaluates a menu by its best element. Such an individual's behavior is represented by a utility function U of the form 



Desire for commitment is an implication of temptation. An individual may strictly prefer menu A to menu 

Axiom 4 relaxes Strategic Rationality and allows a possibility that



Gul and Pesendorfer [3] showed the following representation theorem.
Theorem 1. 


3. Geometry of Temptation and Self-Control
This section explores some geometric properties of 
Lemma 0. (Gul and Pesendorfer ( [4] , Lemma 1)). 


We define u by 

Consider a nontrivial preference relation


A weak temptation relation T is defined by 

A strong temptation relation 


A weak resistance relation R is defined by 

A strong resistance relation 


Two temptation relations display a desire for commitment in a binary menu. Suppose




The next fact is worth pointing out, and we may use this fact repeatedly without warning below: When 





The following properties of four relations are the fundamentals for our geometric approach.
Lemma 1. Suppose that satisfies Preference, Continuity, Independence, and Set Betweenness. Then, the following hold.
Four relations T, 

The weak temptation relation T and the weak resistance relation R are Strong Archimedean.6
We now consider geometric representations of the four strict partial orders. Define four cones corresponding to the four relations as follows.7
A weak temptation cone is defined by
A strong temptation cone is defined by
A weak resistance cone is defined by
A strong resistance cone is defined by
Temptation cones are defined as the set of “tempting directions”, and resistance cones are defined as the set of “resisting directions”. Corresponding to Lemma 1, those cones possess the following properties.
Lemma 2. Suppose that 
Then, the following hold.
Four cones




The weak temptation cone 

4. A Geometric Proof for the Gul and Pesendorfer Theorem
In this section, we prove that any regular self-control preference relation admits a Gul and Pesendorfer representation.
If 






We first obtain two functions that represent temptation and self-control.
Lemma 3. There exist 






Proof. We can prove this lemma in much the same way as in Abe ( [4] , Section 4), and hence omit the detail of proof here. A sketch of proof is provided in Appendix. In there, the proof goes as follows. We openly separate 



We call function v a temptation utility and w a self-control utility.Suppose that


Lemma 4. The self-control utility w must be written by 


Proof. As stated above, when









Because 















Therefore, by the Harsanyi additive representation


Lemma 4 means that the indifference curve of w lies between those of u and v when they pass a common point. From Lemma 4 together with Lemma 3, we further find the following fact that the self-control utility and the temptation utility exactly characterize temptation and costly self-control. The proof is immediate and thus omitted.
Lemma 5. 


We now characterize U using w and v. The next lemma essentially characterizes the functional form of U.
Lemma 6. 


Proof. It immediately follows from Lemmas 1 and 5 that 



Let us now show that, for any


























This lemma says that the ranking of 


Suppose



ment utility is the difference between the self-control utility and a scale-normalized temptation utility:

Figure 1. The Marschak-Machina triangle and Indifference curves of
value of 





Formally, we prove the following.
Lemma 7. Define 







Proof. Since 








where the first equality follows from Lemma 6, the second from Lemma 3, and the third and the last from Lemma 4. This completes the proof.
Remark. Until now, we have focused on regular self-control preferences. Let us comment about the other cases. As heretofore, suppose that 
We first consider the case that 









Let us then consider the case of self-control preferences but not regular. There are three cases: (i) 









Consider finally case (iii). In this case, 


5. Discussion
We provided an alternative proof of the Gul and Pesendorfer’s utility representation theorem about temptation and self-control. In what follows, we clarify relations between our geometric approach and the Gul and Pesendorfer’s original approach.
Gul and Pesendorfer [3] proved the theorem in a way different from ours. Their approach is constructive. They directly define the temptation utility by 





The constructive approach and the geometric approach taken here bring us additional but different benefits beyond just establishing the representation theorem.24 The former directly tells us how to calibrate temptation. On the other hand, the latter directly defines temptation and self-control in terms of preferences, so that it directly relates temptation and self-control utilities to particular intuitive properties of the underlying preferences.
The direct link between the two utilities and preferences promotes a better understanding of the Gul and Pesendorfer model. It highlights the reason why the self-control part can be written by sum of commitment utility and temptation utility. It is because we directly proved that all three dynamic considerations have linear structure and self-control considerations lie between commitment and temptation.
Moreover, the link provides the refined testable implications of the model. Our characterization of T, 



Second, more importantly, because temptation utility v and self-control utility w are characterized by T, 



Acknowledgements
I would like to thank Fumio Dei, Hisao Hisamoto, Eiichi Miyagawa, and especially Hideo Suehiro, for their valuable comments and encouragement. I would also like to thank the anonymous reviewers for their many insightful comments and suggestions. Needless to say, the responsibility for any remaining errors rests with the author. This paper was supported by JSPS KAKENHI Grant Number 16K21038.
Cite this paper
Koji Abe, (2016) A Geometric Approach to Temptation and Self-Control. Theoretical Economics Letters,06,539-548. doi: 10.4236/tel.2016.63060
References
- 1. Gul, F. and Pesendorfer, W. (2004) Self-Control, Revealed Preference and Consumption Choice. Review of Economic Dynamics, 7, 243-264.
http://dx.doi.org/10.1016/j.red.2003.11.002 - 2. Lipman, B.L. and Pesendorfer, W. (2013) Temptation. In: Acemoglu, D., Arellano, M. and Dekel, E., Eds., Advances in Economics and Econometrics: Tenth World Congress Volume 1, Cambridge University Press, New York, 243-288.
http://dx.doi.org/10.1017/CBO9781139060011.009 - 3. Gul, F. and Pesendorfer, W. (2001) Temptation and Self-Control. Econometrica, 69, 1403-1435.
http://dx.doi.org/10.1111/1468-0262.00252 - 4. Abe, K. (2012) A Geometric Approach to Temptation. Journal of Mathematical Economics, 48, 92-97.
http://dx.doi.org/10.1016/j.jmateco.2012.01.002 - 5. Kreps, D.M. (1988) Notes on the Theory of Choice. Westview Press, Boulder.
- 6. Kopylov, I. (2009) Temptations in General Settings. The B.E. Journal of Theoretical Economics, 9, (Advances), Article~31.
http://dx.doi.org/10.2202/1935-1704.1558 - 7. Harsanyi, J.C. (1955) Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility. Journal of Political Economy, 63, 309-321.
http://dx.doi.org/10.1086/257678 - 8. Kelly, J.L. (1975) General Topology. Springer-Verlag, New York.
- 9. Chatterjee, K. and Krishna, R.V. (2008) A Geometric Approach to Continuous Expected Utility. Economics Letters, 98, 89-94.
http://dx.doi.org/10.1016/j.econlet.2007.04.011 - 10. Dekel, E., Lipman, B.L. and Rustichini, A. (2009) Temptation-Driven Preferences. Review of Economic Studies, 76, 937-971.
http://dx.doi.org/10.1111/j.1467-937X.2009.00560.x - 11. Kopylov, I. (2009) Finite Additive Utility Representations for Preferences over Menus. Journal of Economic Theory, 144, 354-374.
http://dx.doi.org/10.1016/j.jet.2008.06.003 - 12. MacCrimmon, K.R. and Larsson, S. (1979) Utility Theory: Axioms versus ‘Paradoxes’. In: Allais, M. and Hagen, O. Eds., Expected Utility Hypotheses and the Allais Paradox, D. Reidel Publishing Company, Dordrecht, 333-409.
http://dx.doi.org/10.1007/978-94-015-7629-1_15 - 13. Machina, M.J. (1983) Generalized Expected Utility Analysis and the Nature of Observed Violations of the Independence Axiom. In: Stigum, B.P. and Wenstop, F., Eds., Foundations of Utility and Risk Theory with Applications, D. Reidel Publishing Company, Dordrecht, 263-293.
http://dx.doi.org/10.1007/978-94-017-1590-4_15 - 14. Noor, J. and Takeoka, N. (2015) Menu-Dependent Self-Control. Journal of Mathematical Economics, 61, 1-20.
http://dx.doi.org/10.1016/j.jmateco.2015.07.004 - 15. Holmes, R.B. (1975) Geometric Functional Analysis and Its Applications. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4684-9369-6
Appendix
Proof of Lemma 3 (Sketch). We first claim:
Claim 2.
Since




Claim 3. There are two linear functional 








Note from Lemma 2 that 











Define functions v and w on Δ by 








Claim 4.
For








Similarly, using lower semi-continuity of U and the fact that 

Supplement to the proof of Lemma 6. As we showed in Section 4, 

Let us show that, for any


Step 1. We show that there exist 


By regularity, there are 

















Step 2. Take 





Suppose to the contrary that 

















Consider now translations 


















Fix such a 






where the last equality follows from Lemma 3. This is a contradiction.
Step 3. For any 



By Step 1, there are 






Supplement to the proof of Lemma 7. We legitimate what we wrote in footnote 20. Observe first that there are 

































Then, by proof of Lemma 7, we have







NOTES
1See Kreps [5] .
2Gul and Pesendorfer [3] consider an extended preference relation over lotteries of menus that is defined in an obvious way and show that Axioms 1 to 3 naturally induce the same properties to the extended relation. They then obtain a function U as a von Neumann and Morgenstern preference-scaling function for expected utility representation of that relation and show by construction that U is indeed a continuous affine function.
3Alternatively, we can rely on [6] to prove Lemma 0. Kopylov [6] applies the mixture space theorem to 


4The fact that these orders are strict partial orders is proved in Lemma 1 below.
5A binary relation R is said to be Asymmetric when 






6A binary relation R is Strong Archimedean if 



7We need a linear space for defining those cones. Here, we take the linear space (over
8Consider a binary relation R on a domain. Let




9A face of a convex cone C is a nonempty convex subset F of C such that 



10From Lemma 2, this is equivalent to the fact that there are 


11This commitment utility u is defined in Section 3.
12We can similarly show that 

13To see it, note that 








14Assuming the existence of such 
15There is no loss of generality as for the footnote above. See Appendix for the detail.
16Function f on 





17Similarly, the ranking of 

18Suppose that u and v are continuous affine functions on Δ. Let U be a continuous function that represents some 

19The other cases are straightforward.
20In general, for arbitrarily fixed 






21Take an 



22We note that our geometric approach does not work well in this degenerate case. Specifically, in the proof of Lemma 7, we cannot take a z by which we calibrate utility value of
23Kopylov [6] proved Theorem 1 for a more general choice object than the one considered here and applied it to characterize various models associated with temptation. In his proof, he also constructs the temptation utility directly in the same spirit with Gul and Pesendorfer [3] by




24As Gul and Pesendorfer ( [3] , footnote 6) conjecture, there is another approach to prove Theorem 1 which is based on a representation theorem characterizing a general model called a finite additive expected utility representation. See Dekel, Lipman, and Rustichini [10] for the case of finite Z and Kopylov [11] for a more general choice object.
25As in the literature of non-expected utility theories, identifying the nature of violations of a particular model (expected utility model in the literature) is an important issue in order to develop a new model that accommodates the violations. See MacCrimmon and Larsson [12] and Machina [13] . In the literature of temptation, Noor and Takeoka [14] extend the Gul and Pesendorfer model to admit an individual’s ability to exert self-control to depend on the faced menu. Providing a minimal generalization to the Gul and Pesendorfer model, they retain linearity of temptation utility. To this end, they characterize linear temptation utility in a way similar to ours.








