Journal of Mathematical Finance
Vol.2 No.3(2012), Article ID:22109,11 pages DOI:10.4236/jmf.2012.23024
Pricing Options on Foreign Currency with a Preset Exchange Rate
Department of Economics and Finance, Baruch College, New York, USA
Email: er.wolf@baruch.cuny.edu, Christopher.hessel@baruch.cuny.edu
Received May 4, 2012; revised June 8, 2012; accepted June 15, 2012
Keywords: Garman Kolhagen; Option Pricing; Currency; Foreign Exchange; Hedging; Speculating; Preset Exchange Rate
ABSTRACT
This paper presents a new option that can be used by agents for managing foreign exchange risk. Unlike the Garman Kolhagen model [1], (GK), this paper presents a new model with a preset exchange rate (PE), that allows the agent to take advantage of the his/her view on both the direction and magnitude of rate movement and as such provides this agent with more choices. The model has a provision for an automatic exchange of the payoff at a preset exchange rate, and upon expiration gives the agent the choice of keeping the payoff in the foreign currency or exchanging it back to the pricing currency. At the time of writing, the buyer selects the preset exchange rate. Depending on the value selected, the PE option’s price and payoff will be equal to, greater than or less than those of the GK model. A decision rule for choosing between the PE and GK models is developed by determining the expiration spot rate that equates the two models’ returns. The range of spot rates that makes the PE option’s return greater than the GK’s return is the PE preferred range. If the agent expects the expiration spot rate will be within the preferred range, the PE option is purchased. The size of the preferred range is a decreasing function of time to expiration, a decreasing function of spot rate volatility and an increasing function of the basis point spread between foreign and domestic interest rates.
1. Introduction
The options markets have grown tremendously since the introduction of Chicago Board Options Exchange (CBOE) in 1973. With the introduction of International Securities Exchange (ISE), the first electronic exchange in the USA, the market received a significant boost and the options markets reached new heights. The equity options daily volume in 1997 was 1.079 million contracts, and at the end of the 1st quarter of 2011, the volume was 17.609 million contracts for an average annual growth rate of 21.8%1. The foreign exchange (FX) options also grew rapidly. The FX option notional amount in 1995 was $0.8 billion and by 2010 was $12.1 billion, for an average annual growth rate of 39.74%2.
To a great degree growth of options trading was made possible due to the applicability of options pricing models developed in the seminal papers of Black and Scholes (BS) [3,4], and Merton [5] which created a new era and renewed interest in options pricing and has inspired researchers to expand the pricing model in many directions including correcting for the unrealistic assumption of constant volatility. Hull and White [6,7], Ritchken and Trevor [8] and Wiggins [9] generalized the constant volatility models to allow for stochastic volatility. Heston and Nandi [10] develop a closed-form single lagged GARCH model. Later Christoffersen, Heston and Jacobs [11], and Mercuri [12] extended Heston and Nandi’s model, where Christoffersen et al. utilizes inverse Gaussian innovations and Mercuri utilizes tempered stable innovations. Barone-Adesi, Rasmussen and Ravanelli [13] value the stock option using a GARCH diffusion model. While Badescu and Kulperger [14] capture skewness and leptokurtosis observed in stock price data. Gong, Thavaneswaran and Singh [15,16] model the expiration call price as the expected price of a truncated normal distribution. The need to capture the radical changes in volatility over time lead to the development of jump and switching models. Elliot, Sui and Chan [17] present change in volatility as a switching Markov process with the transition accomplished through an Esscher transformation. Both Thavaneswaran and Singh (TS) [18,19] and Pillay and O’Hara’s [20] (PH) incorporate the lognormal distribution. TS has a jump diffusion model with stochastic volatility, where the expiration price is a moment of a truncated log-normal distribution and PH has the stock price follow a mean reverting log-normal process with stochastic diffusion and jumps and the option’s price determine by fast Fourier transformation methodology. Makate and Sattayatham [21] have stock price follow a jump diffusion process with square root stochastic volatility and mean reversion, and Sarisa Pinkham, Pairote & Sattayatham [22] model change in stock price as a linear combination of the time-change Lévy process and the Vasicek stochastic interest rate process. Much of these innovations are discussed in Gong, Thavanewswaran and Liang [23] where they use partial differential equations for various stochastic diffusion models to study option pricing with the pure jump process, jump diffusion process, stochastic volatility and jump diffusion with stochastic volatility. Ivancevic [24] shifts from the Black and Scholes option pricing equation to a Kolmogorov probability approach to develop an adaptive waveform nonlinear stochastic option pricing model.
Leaving the realm of option pricing for stock and stock indices, GK [1] extended the BS model to price options on foreign currencies. For over a quarter of a century, the GK option-pricing model has been the standard foreign currency option-pricing model in pricing European style options and the base for modified pricing formulation for American style options. In 2007 Ahn, Cho and Park [25] took issue with the constant volatility assumption in GK and modeled volatility as a jump diffusion process to address pricing currency options under shocks such as large changes in the monetary system introduced by central banks or catastrophic events such at 9/11, Hurricane Katrina and the tsunami that struck Japan. This paper moves in a different direction and presents a currency option that enhances the set of choices for the participating agents. Based on economic theory, moving the choice set towards a complete one helps to improve the well-being of the participating agents by allowing them to move to a higher utility function. In this paper, we introduce the Preset Exchange rate option model. The PE option model has three distinct characteristics: 1) The option’s user sets the automatic exchange rate, “E”, which converts the premium currency payoff to the foreign currency payoff; 2) The option’s buyer has the choice of keeping the payoff in the foreign currency or changing it to the premium currency at the spot rate; and 3) If the anticipated spot rate change occurs, the return from the PE option exceeds the return of the GK option.
A specific value of E makes the PE value identical to that of GK. We term that value of E, the breakeven point and designate it EBE. Not only is the price the same, but if the expiration spot rate equals EBE, the payoffs are the same. The agent, who chooses between the PE options or the GK options, bases the decision on whether the agent expects the expiration spot rate will be greater or less than EBE. As with any option, the value paid is lost, if the option expires out-of-the-money. With the PE options setting E > EBE, causes the PE option value < GK value, and setting E < EBE, causes the PE option value > GK value. The agent can alter the price (exposure to loss should the option expire out-of-the-money) by the selection of E. This is a characteristic not available in the GK options. Both price and payoff are inversely related to the size of E. For , the criteria, for choosing between the two option models, is based on percent return on investment. By determining the expiration spot rate,
, the criteria, for choosing between the two option models, is based on percent return on investment. By determining the expiration spot rate,  , that equates the percent return on investments for the two models, the criteria for choosing between the PE model and the GK model is identified. The choice is based on whether the agent expects the expiration spot price will be greater than or less than
, that equates the percent return on investments for the two models, the criteria for choosing between the PE model and the GK model is identified. The choice is based on whether the agent expects the expiration spot price will be greater than or less than . Of importance to the agent is the size of the range of spot rates that makes the PE the favorable choice. Both the value of
. Of importance to the agent is the size of the range of spot rates that makes the PE the favorable choice. Both the value of  and its proximity to the strike rate is a function of the option’s term, rate volatility and the basis point spread between the foreign currency interest rate and the domestic currency interest rate.
and its proximity to the strike rate is a function of the option’s term, rate volatility and the basis point spread between the foreign currency interest rate and the domestic currency interest rate.
The remainder of the paper is organized in five parts. We begin by presenting payoff values for the PE call and put options, and compare them to the payoffs values for the GK calls and puts. Using numerical examples, we demonstrate the impact of changing the value of E on the PE call, put prices, and present the EBE for both options. We start the analysis with the special case E = EBE and present a decision rule for the agent to use to choose between ownership of or writing of PE and GK model options. We then extend the analysis to  that allows the development of a more general decision rule for choosing between ownership or writing of PE or GK options written for differing terms, written during differing levels of volatility and written during differing size spreads between the domestic currency and foreign currency interest rates. Next, we present the procedure for calculating price, payoff, and the necessary decision rule for implementation of the model. The final section is the conclusion.
that allows the development of a more general decision rule for choosing between ownership or writing of PE or GK options written for differing terms, written during differing levels of volatility and written during differing size spreads between the domestic currency and foreign currency interest rates. Next, we present the procedure for calculating price, payoff, and the necessary decision rule for implementation of the model. The final section is the conclusion.
2. Payoff of the PE Options
This section presents the payoffs for both the GK and the PE models. The analysis of the payoff is a necessary step in developing the pricing formula for the PE. As such, the PE payoffs are presented in two stages: first, with the payoff in the foreign currency and second, after converting the foreign denominated payoff to the domestic using the expiration spot rate. We then compare the PE and GK pricing formula. Lastly, we compare the two models in terms of return on investment.
Generally, the payoffs of the call and the put under the PE setting, prior to converting the payoff to the domestic currency are:
 (1)
(1)
 (2)
(2)
where:
S* is the prevailing domestic exchange rate upon expiration, for example in the US could be the US dollar per Euro exchange rate (EUR/$) upon the option’s expiration date.
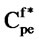 is the PE call payoff in the foreign currency upon expiration.
is the PE call payoff in the foreign currency upon expiration.
 is the PE put payoff in the foreign currency upon expiration.
is the PE put payoff in the foreign currency upon expiration.
K—The strike price.
E—The preset exchange rate.
The payoffs in the domestic currency using the expiration rate S* are:
The call payoff is:
 (3)
(3)
The put payoff in domestic currency is:
 (4)
(4)
where:
 —The PE call payoff in the domestic currency upon expiration and:
—The PE call payoff in the domestic currency upon expiration and:
 —The PE put payoff in the domestic currency upon expiration In comparison, the standard GK expiration date payoff for calls and puts are as follows:
—The PE put payoff in the domestic currency upon expiration In comparison, the standard GK expiration date payoff for calls and puts are as follows:
 (5)
(5)
And:
 (6)
(6)
3. Pricing Formula of the PE Options
Hart and Ross [26] introduced the concept of options with continuous strike prices. In their paper, they constructed a portfolio of European call options with different strike prices, but in all other respects identical. In HR, the strike prices are set so that the most expensive call option is the one constructed with the lowest strike price.
Thereafter, each subsequent option in the portfolio is set with a different strike price that is higher than the previous one by DK.
For all  the portfolio’s payoff upon expiration becomes:
the portfolio’s payoff upon expiration becomes:
 (7)
(7)
As DK, the incremental strike price approaches zero, the approximation of the portfolio’s payoff approaches:
 (8)
(8)
We multiply and divide Equation (8) by E and rearranging it to get:
 (9)
(9)
Based on the above, the PE call option value can approximately be replicated constructing the following portfolio:
A long position in 2/E equally weighted portfolio of European call options where the lowest strike price in this portfolio is K and the strike price of each subsequent call option is greater than its previous one by DK, and a long position in K/E European call option with a strike price of K.
Accuracy of duplicating the payoff of the original call option by constructing the above-mentioned portfolio depends on one’s ability to substantively reduce DK, if possible close to zero, and simultaneously to increasing number of European call options in the approximating portfolio.
With this in mind and using BS [5] pricing setting, the underlying price process S(t) can be described by the following equation:
 (10)
(10)
where:
t—Time to expiration expressed as a fraction of a year.
S—Current exchange rate.
rd—Domestic interest rate.
rf—Foreign interest rate.
s—Standard deviation of S rate of change.
E—Preset expiration exchange rate.
w(t)—Standard Weiner process.
Define y as follows:
 where:
where:

The call option value can be calculated as the expected discounted risk neutral of the option’s payoff:
 (11)
(11)
After integration, we get:
 (12)
(12)
Rearranging terms on the right had side of Equation (12) yields:
 (13)
(13)
where:
 is the cumulative standard normal distribution function of
is the cumulative standard normal distribution function of ; and:
; and:
 (14)
(14)
The put’s price can is derived using the same procedure as the one used for the call:
 (15)
(15)
where:
 (16)
(16)
In comparison, the GK model results in the following pricing formula:
 (17)
(17)
 (18)
(18)
where:
 (19)
(19)
 (20)
(20)
4. Comparison of the PE and GK Models Using Numerical Illustrations
The PE model expands the dimension of possibilities for the participants, including investors, hedgers, and speculators and makes the market more complete. The participant chooses between leaving the payoff in the foreign currency, or converting it to the pricing currency. The participant selects the value of E that determines the price, which is the potential loss, should the option expire out of the money. The participant speculates on more than direction of change, but also magnitude of change. If the expiration spot rate is within a specified range, the owner of the PE option earns a higher return on investment than a comparable investment in the GK option, regardless of the specification of E. All of these differences between the PE and GK models are shown in this section.
4.1. Price Comparisons
We compare call prices using Equations (13) for PE and (17) for GK and put prices using Equations (15) for PE and (18) for GK and then compare the payoffs for calls and puts using Equations (3) and (4) for PE options, and (5) and (6) for GK options.
By selecting the preset exchange rate E, the option buyer sets the price and resulting exposure to losses should the option expire out-of-the-money. Figure 1 focuses attention on the relationship of E on the value of at-the-money PE call option’s value and how the PE option’s value compares with the GK call option’s value. In Figure 2 the analysis is repeated forat-the-money PE and GK putoptions.For the illustrations s = k = 1.00, σ = 10%, t = 1.0 years, rd = rf = 7%.
The intersection of the lines is the value of E that equates price, or exposure, EBE.

Figure 1. Comparison of call prices for differing E values. The horizontal axis shows the preset exchange rates for atthe-money PE and GK call options. While the vertical axis shows the option price. S = K = 1.00, σ = 10%, t = 1.0 years, rd = rf = 7%.
Figure 1 shows the existence of an inverse relationship between E and price. The EBE for our illustration is 1.14. For E greater than 1.14, the PE call costs less than the GK call. While for E less than 1.14, the PE call is more expensive. The line shows slight convexity indicating as E is lowered, the price increases at an increasing rate, albeit it the increase is very small.

Figure 2. Comparison of put prices for differing E values. The horizontal axis shows the preset exchange rates for atthe-money PE and GK put options. While the vertical axis shows the option price. S = 1.00, σ = 10%, t = 1.0 years, rd = rf = 7%.
Figure 2 shows a similar relationship between E and the put price. As in the case of the call, an inverse relationship exists between the E value and put price. There is a value of E that equates the prices of the PE and GK puts. EBE occurs at the intersection of the lines, and for this illustration EBE = 0.88.
For E less than EBE, (0.88), the PE put price exceeds that of the GK put and for E greater than EBE the PE put price is less than the GK put price. As in the case of the call, the E-Price line is slightly convex indicating as E is lowered the price increases at an increasing rate.
4.2. Payoff Comparisons
We continue to use the same values of S, σ, t rf and rd when comparing payoffs. The PE call payoffs are shown for three values of E: E = 0.95, which is below the origination spot rate 1.00, E = 1.05, which is above the origination spot rate and EBE = 1.135.

Figure 3. Comparison of call payoffs. The horizontal axis shows the exchange rates at expiration, which are 0.90, 1.00, 1.05, 1.10, and 1.15. Strike is 1.00. The preset exchange rate E is set to three values, 1.135, the rate that equates the PE and GK prices, 1.05 a little higher than the spot rate at time of writing and 0.95 a little lower than the spot rate at time of writing. The lines are labeled GK and the three values of E for the PE calls. The PE payoff is (S* – K)(S*/E). The (S*/E) component makes the payoff non-linear in S*.
Examination of Figure 3 reveals the payoff lines to the right of 1.00 are slightly curved as compared with the straight 45˚ angle of the conventional call. For the PE call, payoff increases at an increasing rate albeit at a small rate of increase. S* is the spot rate at expiration and K is the strike rate. The call payoff for the GK call is  and for the PE call
and for the PE call . The PE payoff is equal to the GK payoff when S* = E. For all values of S* > E the PE payoff is larger while for S* < E the PE payoff is smaller.
. The PE payoff is equal to the GK payoff when S* = E. For all values of S* > E the PE payoff is larger while for S* < E the PE payoff is smaller.
This relationship is most easily seen at EBE = 1.135, which equates the two models’ values. For expiration spot rate, S* > 1.135, the PE call was purchased for the same price as the GK call, but has a larger payoff than the GK call. For S* < 1.135, the PE call has the smaller payoff. Agents have a basis for choosing between the PE and GK call. If the agent is a hedger that hedges cash flows and has the view that S* > 1.135, he will buy the PE option, while if the view is S* < 1.135 the agent will buy the GK call. An agent willing to write options to increase portfolio income and has the expectation S* < 1.135 will choose to write PE calls over GK calls. This is because the writer receives the same price from both calls, but if S* < 1.135, the PE writer makes a smaller payout to the agent owner then if the GK call had been written.
When E is set for a value less than EBE, both the PE’s price and payoff will exceed those of the GK call while for value of E > EBE, both the PE’s price and payoff will be less than those of the GK call. To determine the value of S* in these situations, a different analysis is required. One involving return on price and is presented in Section 4.3 immediately after the comparison of put payoffs.
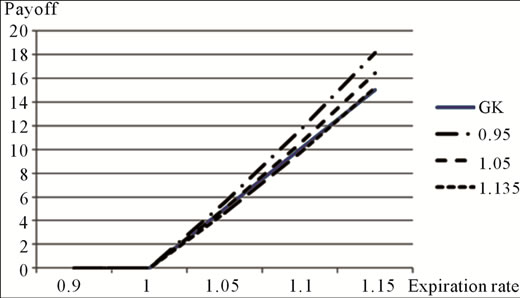
Figure 4. Comparison of put payoffs. The five expiration exchange rates range from 1.05 down to 0.85. For all puts, the strike is 1.00. For the PE puts the preset exchange rate E are 0.95, 0.884 and 0.75 where 0.884 is the value of E that makes the PE put price the same as the GK put price. The GK line is labeled GK while the three PE put lines are labeled based on their E values.
Figure 4 shows a comparison of PE and GK put payoffs for differing values of E. On the horizontal axis, we show five expiration spot rates ranging from 1.05, above the spot rate (1.00), down to 0.85.
Three PE puts are shown differing in E value; E = EBE = 0.884, E = 0.95, between the strike rate and EBE and E = 0.75 which is below EBE. Examining the payoff lines for the PE puts starting at-the-money and moving in-tothe-money, we notice all three lines are nonlinear. Focusing on the payoff line E = EBE = 0.884, the payoff is initially larger than that of the GK put and as the option moves deeper into the money the payoff line crosses the GK payoff line and continues to increase but is be below the GK payoff line. For spot rates where the PE put has the larger payoff, the PE put has the larger return on investment. The PE puts payoff is . The GK put payoff is
. The GK put payoff is . The expiration spot rate that equates payoffs is S* = E and in this illustration is S* = 0.884. For expiration spot rate between the strike and EBE, the PE put payoff exceeds the GK payoff, while for expiration spot rates below EBE, the PE put payoff is less than that of the GK put. This leads to a decision rule. Participants should purchase the PE put or GK put based on whether the participant’s view of the expiration spot rate is that it will be above or below EBE. Writers always expect the payoff will be less than the price received or they would not be writing the option. For this illustration the writer’s breakeven spot rate for the PE put is 0.966 while for the GK put it is 0.963. If the spot rate is expected to fall but not below 0.966, the writer is indifferent to writing either model’s put. If the writer expects the expiration spot rate will be between, 0.966 and 0.963, the writer will prefer to write the GK put. Below 0.963, the writer has returned the full price to the buyer and has begun to lose money. Looking at the put lines for E = 0.95, the payoff is less than the GK payoff but its price is less. While for E = 0.75 the payoff exceeds the GK payoff but so does its price. Analysis of the calls and puts with
. The expiration spot rate that equates payoffs is S* = E and in this illustration is S* = 0.884. For expiration spot rate between the strike and EBE, the PE put payoff exceeds the GK payoff, while for expiration spot rates below EBE, the PE put payoff is less than that of the GK put. This leads to a decision rule. Participants should purchase the PE put or GK put based on whether the participant’s view of the expiration spot rate is that it will be above or below EBE. Writers always expect the payoff will be less than the price received or they would not be writing the option. For this illustration the writer’s breakeven spot rate for the PE put is 0.966 while for the GK put it is 0.963. If the spot rate is expected to fall but not below 0.966, the writer is indifferent to writing either model’s put. If the writer expects the expiration spot rate will be between, 0.966 and 0.963, the writer will prefer to write the GK put. Below 0.963, the writer has returned the full price to the buyer and has begun to lose money. Looking at the put lines for E = 0.95, the payoff is less than the GK payoff but its price is less. While for E = 0.75 the payoff exceeds the GK payoff but so does its price. Analysis of the calls and puts with  is presented next.
is presented next.
4.3. Return on Investment Comparison
For values of , the PE option is either more or less expensive than the GK option. To address financial equality of the two option models, payoff comparisons are not sufficient. Payoff must be related to price. In this section, we compare the PE call to GK call and PE put to GK put by comparing return on investment. To this end, we calculate the PE option’s price for a given value of E and the GK option price. The payoffs for both the PE and GK options are calculated. Using the price and payoff values, we calculate buyer’s percentage return on investment, [(payoff – price)/price]. To compare the returns on investment from the PE and GK options, we calculate excess (percent) return,
, the PE option is either more or less expensive than the GK option. To address financial equality of the two option models, payoff comparisons are not sufficient. Payoff must be related to price. In this section, we compare the PE call to GK call and PE put to GK put by comparing return on investment. To this end, we calculate the PE option’s price for a given value of E and the GK option price. The payoffs for both the PE and GK options are calculated. Using the price and payoff values, we calculate buyer’s percentage return on investment, [(payoff – price)/price]. To compare the returns on investment from the PE and GK options, we calculate excess (percent) return, . Positive excess return means ROIPE > ROIGK, while negative excess return means ROIPE < ROIGK. The expiration spot rate that equates the returns is
. Positive excess return means ROIPE > ROIGK, while negative excess return means ROIPE < ROIGK. The expiration spot rate that equates the returns is . To facilitate the analysis, we relate the expiration spot rate, S* to the origination spot rate S, using a multiplier, M, times the origination time weighted standard deviation,
. To facilitate the analysis, we relate the expiration spot rate, S* to the origination spot rate S, using a multiplier, M, times the origination time weighted standard deviation, . For calls the expiration spot rate is:
. For calls the expiration spot rate is:
 (21)
(21)
and for puts is:
 (22)
(22)
The value of M that results in  is MBE. To determine MBE, optimizing software like Excel’s “Goal Seek” or “Solver” is used to change the value of M until excess return equals zero. For M ≠ MBE,
is MBE. To determine MBE, optimizing software like Excel’s “Goal Seek” or “Solver” is used to change the value of M until excess return equals zero. For M ≠ MBE,  , one of the two option models gives the buyer a higher return on investment, making it the preferred option. Analysis in this section focuses on how each of three variables impacts
, one of the two option models gives the buyer a higher return on investment, making it the preferred option. Analysis in this section focuses on how each of three variables impacts  and by extension
and by extension , thereby impacting the relative attractiveness of PE options. The variables are: origination term, origination σ and the spread between the foreign and the domestic currency interest rates at the time of option writing. We present our findings for calls and puts starting with origination term (Figures 5 and 6), origination volatility (Figures 7 and 8) and spread between interest rates (Figures 9 and 10).
, thereby impacting the relative attractiveness of PE options. The variables are: origination term, origination σ and the spread between the foreign and the domestic currency interest rates at the time of option writing. We present our findings for calls and puts starting with origination term (Figures 5 and 6), origination volatility (Figures 7 and 8) and spread between interest rates (Figures 9 and 10).
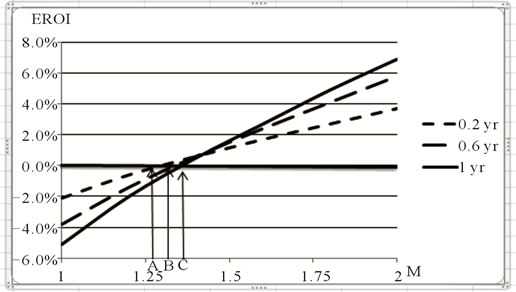
Figure 5. Call excess return versus term. ROEc = (Payoffc – Pricec)/Pricec. Excess return = . Both E = 1.00 and σ = 10% are held constant for the analysis, t = 0.5 years and rd = rf = 7%. The expiration spot rate
. Both E = 1.00 and σ = 10% are held constant for the analysis, t = 0.5 years and rd = rf = 7%. The expiration spot rate , where M is increased from 1.00 to 2.00 causing the S* > S by m time adjusted standard deviations. The excess return, EROI, is on the vertical axis and “M” is the horizontal axis. The lines are for calls with initial terms of 0.2 years, 0.6 years, and 1.0 year. The points where the returns of the two models are the same,
, where M is increased from 1.00 to 2.00 causing the S* > S by m time adjusted standard deviations. The excess return, EROI, is on the vertical axis and “M” is the horizontal axis. The lines are for calls with initial terms of 0.2 years, 0.6 years, and 1.0 year. The points where the returns of the two models are the same,  , are shown at points A (0.20 years) MBE = 1.30, B (0.60 years) MBE = 1.34 and C (1.0 years) MBE = 1.36.
, are shown at points A (0.20 years) MBE = 1.30, B (0.60 years) MBE = 1.34 and C (1.0 years) MBE = 1.36.
Figure 5 shows the excess return lines for three origination maturities, 0.2 years, 0.6 years, and 1.0 years. The vertical axis shows excess return and the horizontal axis shows M values. The solid horizontal line shows excess return equal to zero. The intersections of PE excess return lines with the horizontal line are the MBE values.

Figure 6. Put excess return versus term. ROEp = (Payoffp – Pricep)/Pricep. Excess return = . Expiration rate
. Expiration rate . The percent excess return, EROI, is shown on the vertical axis and the values of M are shown on the horizontal axis. σ = 10% and E = 1.0, t = 1.0 years and rd = rf = 7%. The points where the returns of the two models are the same,
. The percent excess return, EROI, is shown on the vertical axis and the values of M are shown on the horizontal axis. σ = 10% and E = 1.0, t = 1.0 years and rd = rf = 7%. The points where the returns of the two models are the same,  , are shown at points A (0.20 years) M = 1.21, B (0.60 years) M = 1.18 and C (1.0 years) M = 1.16.
, are shown at points A (0.20 years) M = 1.21, B (0.60 years) M = 1.18 and C (1.0 years) M = 1.16.
Figure 6 shows the range of expiration spot rates (M values) for which ROIPE > ROIGK, consists of all values of M > MBE. The smaller the value of MBE, the closer  is to the initial spot rate S, the greater the likelihood
is to the initial spot rate S, the greater the likelihood . The values of S* such that
. The values of S* such that , is called the PE preferred range meaning the PE call is desired over the GK call.
, is called the PE preferred range meaning the PE call is desired over the GK call.

Figure 7. Call percent excess return versus volatility. ROEc = (Payoffc – Pricec)/Pricec. Excess return =  . Both E = 1.00 and term = 1.0 years are held constant for the analysis. The percent excess return, EROI, is on the vertical axis and the number of standard deviations S* > S is on the horizontal axis. Each call is written ATM. Each line represents a different initial volatility. The points where the returns of the two models are the same,
. Both E = 1.00 and term = 1.0 years are held constant for the analysis. The percent excess return, EROI, is on the vertical axis and the number of standard deviations S* > S is on the horizontal axis. Each call is written ATM. Each line represents a different initial volatility. The points where the returns of the two models are the same,  , are shown at points A σ = 5% M = 1.29, B σ = 10% M = 1.33 and C σ = 15% M = 1.37.
, are shown at points A σ = 5% M = 1.29, B σ = 10% M = 1.33 and C σ = 15% M = 1.37.
Figure 7 shows there is an inverse relationship between term and the size of the PE preferred range and
therefore the likelihood the PE call will have higher ROI than the GK call. When the value of MBE changes, the starting point of the preferred range shifts closer to or further away from the spot rate, widening or narrowing the preferred range. The sensitivity of value of MBE to change in time to expiration (term) is weak. Starting at term 0.6 years, a decline in term by 66.7% (0.6 to 0.2 years), cause the value of MBE to decline by 1.46%. While an increase in term by 66.7% (0.6 to 1.0 years), cause the value of MBE to increase by 1.08%3. Since the percentage change in MBE are not the same, the excess return line exhibits slight convexity. As term is shorten, the value of MBE decreases at a decreasing rate, causing the PE preferred range to widen at a decreasing rate. Time to expiration however has no impact on the decision criteria for choosing between PE and GK options. If the agent/portfolio manager is interested in hedging portfolio value or cash flows and believes the expiration spot rate will exceed , the agent should purchase the PE call, while if this agent expects the spot rate will not exceed
, the agent should purchase the PE call, while if this agent expects the spot rate will not exceed , the agent should purchase the GK call.
, the agent should purchase the GK call.
Figure 6 is a parallel analysis for put options.
The vertical axis shows excess return, the horizontal axis shows M values and the solid horizontal line shows excess return equal to zero. The intersection of PE excess return lines with the horizontal line are the MBE values.
In Figure 6 the put’s PE preferred range consists of values of M where M < MBE. The larger the MBE value,
the larger the PE preferred range. For term 0.20 years MBE = 1.21 while at term 1.0 year MBE = 1.16. As origination term is shortened, the put PE preferred range widens, increasing the likelihood ROIPE > ROIGK and the desirability of the PE put option. As with the call, the impact of term is small. Starting at term 0.6 years, a decline in expiration by 66.7% (0.6 to 0.2 years), cause the value of MBE to increase by 2.54%. While an increase in expiration by 66.7% (0.6 to 1.0 years), cause the value of MBE to decrease by 1.69%. Since the percentage change in MBE are not the same the excess return line exhibits slight convexity. As term is shorten, the value of MBE increases at an increasing rate, causing the PE preferred range to increase at an increasing rate. However, change in term has no impact on the criteria to choose between the PE and GK put. If the agent expects the expiration spot rate will be within the preferred range from the K down to , the agent will buy the PE put.
, the agent will buy the PE put.
Figures 7 and 8 reveal the impact of change in initial volatility on the PE preferred range. Figure 7 looks at the call and Figure 8" target="_self"> Figure 8 looks at the put. Three volatilities are considered, 5%, 10%, and 15%, representing small, medium, and high volatility. For calls, in general, the smaller the M value, the closer 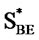 is to S, increasing the likelihood of
is to S, increasing the likelihood of , and widening the PE preferred range by moving its starting value closer to S.
, and widening the PE preferred range by moving its starting value closer to S.
In Figure 7, attention is drawn to two observations, the location of MBE points, and the slopes of the excess return lines. The points of intersections of the excess return lines for the three volatilities and the horizontal zero excess return line, are the MBE values. MBE increases with volatility. At 5% MBE = 1.29 while at 15% MBE is 1.37. However, the relative size of increase in MBE value is small. A 33.3% decrease in initial volatility (10% down to 5%), decreases MBE by 2.56%, while a 33.3% increase in volatility (10% to 15%), increases MBE by 3.01%. As volatility decreases MBE shifts closer to the spot rate, widening the preferred range at a decreasing rate. Shifting attention to the slope of the lines, as S* moves deeper into the preferred range, the slope of the excess line increases at an increasing rate with the rate of increase related to the level of volatility. The 15% excess return line is above and increasing at a faster rate than the 5% excess return line. This raises a tradeoff faced by the agent. As volatility increases the preferred range narrows but the deeper the expiration spot rate moves into the preferred range, the greater the excess return. Although the criteria for choosing between the PE and GK call is the same for all levels of volatility, the agent must evaluate the tradeoff of lower probability of excess return for potentially much larger excess returns as volatility increases.

Figure 8. Put percent excess return verus volatility. ROEp = (Payoffp – Pricep)/Pricep. Excess return = 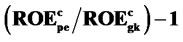 . Expiration rate
. Expiration rate . Percent excess return is shown on the vertical axis and the values of M are shown on the horizontal axis. Term is 0.5 years and E = 1.0. Each put is written ATM. The points where the returns of the two models are the same,
. Percent excess return is shown on the vertical axis and the values of M are shown on the horizontal axis. Term is 0.5 years and E = 1.0. Each put is written ATM. The points where the returns of the two models are the same,  , are shown at points A σ = 5% M = 1.22, B σ = 10% M = 1.19 and C σ = 15% M = 1.15.
, are shown at points A σ = 5% M = 1.22, B σ = 10% M = 1.19 and C σ = 15% M = 1.15.
Figure 8 shows the impact of volatility at time of writing on excess return. As with the call, focus is on both the location of the MBE for each volatility value, and the slope of the lines.
For low levels of volatility (5%), MBE is 1.22 while at high volatility (15%) MBE is at 1.15. The larger the value of MBE, the further  is below the spot rate. Since the range of
is below the spot rate. Since the range of  that makes ROIPE > ROIGK is S* between the strike and
that makes ROIPE > ROIGK is S* between the strike and , larger MBE means larger range for which ROIPE > ROIGK. The PE put is more desirable when the time of writing volatility is low rather than high. If S* at expiration is within the PE preferred range, the excess return is much greater when the option is written during high volatility. As for the call, the relative size of increase in MBE value is small. A 33.3% decrease in volatility at time of writing (10% down to 5%), decreases MBE by 3.36%. While a 33.3% increase in volatility (10% down to 15%), increases MBE by 2.52%. deviations, while at volatility. The asymmetry of the changes in MBE, shows that as volatility increases, MBE increases at a decreasing rate. Turning to the slope of the lines, for increases in spot rate, the slope of the excess return line for volatility 15% is above and much steeper than the excess return line for volatility 5%. The agent’s decision to buy the PE put or the GK put still depends on whether the agent expects the expiration spot rate will be within the PE preferred range or below it. The agent is also confronted with the tradeoff during high volatility of lower likelihood of the spot rate being within the preferred range and the magnitude of excess return if the spot rate is within the preferred range.
, larger MBE means larger range for which ROIPE > ROIGK. The PE put is more desirable when the time of writing volatility is low rather than high. If S* at expiration is within the PE preferred range, the excess return is much greater when the option is written during high volatility. As for the call, the relative size of increase in MBE value is small. A 33.3% decrease in volatility at time of writing (10% down to 5%), decreases MBE by 3.36%. While a 33.3% increase in volatility (10% down to 15%), increases MBE by 2.52%. deviations, while at volatility. The asymmetry of the changes in MBE, shows that as volatility increases, MBE increases at a decreasing rate. Turning to the slope of the lines, for increases in spot rate, the slope of the excess return line for volatility 15% is above and much steeper than the excess return line for volatility 5%. The agent’s decision to buy the PE put or the GK put still depends on whether the agent expects the expiration spot rate will be within the PE preferred range or below it. The agent is also confronted with the tradeoff during high volatility of lower likelihood of the spot rate being within the preferred range and the magnitude of excess return if the spot rate is within the preferred range.
Figures 9 and 10 examine the impact of the spread between the foreign and domestic interest rates on MBE and consequently  and the attractiveness of PE options over GK options. For each set of interest rate values, there is a unique value for MBE. For calls if M > MBE excess return is positive.
and the attractiveness of PE options over GK options. For each set of interest rate values, there is a unique value for MBE. For calls if M > MBE excess return is positive.

Figure 9. Call MBE for combinations of domestic and foreign currency interest rates. For the analysis E = 1.00 and term = 1.0 year, σ = 10%, K = 1.0, S = 1.0 and rf = 7%. The horizontal axis is the value of rd. The vertical axis is MBE. Line “MBE rf = 7%” plots the values of MBE calculated for decreasing values of rd. Line “MBE rd = 7%” plots the values of MBE calculated for decreasing values of rf shown on the horizontal axis.
In Figure 9 there are two lines, solid and dotted. The solid line shows the values of MBE for the foreign rate (rf) fixed at 7.00% and domestic rate (rd) taking on the values on the horizontal axis. Interest rate spread is (rf – rd). At rd = 6% the spread is 7% – 6% = 1%. At rd = 3% the spread is 7% – 3% = 4%. As the spread increases in positive value, the solid line declines, indicating MBE is moving closer to the spot rate. As interest rate spread increases, smaller increases in spot rate are required for ROIPE > ROIGK, making ownership of the PE call more desirable. The reverse is shown by the dashed line, the rd is fixed at 7% and rf takes on values on the horizontal axis. At rf = 6% spread is 6% – 7% = –1% while at 3% the spread is 3% – 7% = –4%. As the spread increases in negativity, MBE increases in size, requiring larger increases in the spot rate for the PE call to be preferred. We have two other observations; first, this finding is independent of the level of the pair of interest rates, and second MBE values are a function of the basis point size of the spread. MBE is 1.27 for a positive spread of 2% regardless of whether pair of rates are rf = 7% and rd = 5% or rf = 5% and rd = 3%.

Figure 10. Put MBE for combinations of domestic and foreign currency interest rates. For the analysis E = 1.00 and term = 1.0 year, σ = 10%, K = 1.0, S = 1.0 and rf = 7%. The horizontal axis is the value of rd. The vertical axis is MBE. Line “MBE rf = 7%” plots the values of MBE calculated for decreasing values of rd. Line “MBE rd = 7%” plots the values of MBE calculated for decreasing values of rf, shown on the horizontal axis.
Figure 10 shows a parallel analysis for the put options. The starting point is where rf = rd =7% and alternately, one of the two rates is lowered. The MBE for each pair of rates is calculated and shown in figure 10. In the case of the put, the spot rate range for which the PE put is preferred to the GK put is from the strike rate down to . As MBE increases in size,
. As MBE increases in size,  shifts further below the strike rate, increasing the range for which ROIPE > ROIGK.
shifts further below the strike rate, increasing the range for which ROIPE > ROIGK.
The solid line shows the values of MBE when the foreign currency interest rate is fixed at 7.00% and domestic currency rate takes on the values on the horizontal axis. Interest rate spread is (rf – rd). As the interest rate spread increases in positive value, MBE increases, (solid line) expanding the expiration spot rate range for which ROIPE > ROIGK. As in the case of the call, the level of interest rates is unimportant but the basis point spread is important. For the same size spread such as 200 basis points, regardless of interest rate level, MBE is the same value.
5. Procedures for the Agent to Follow to Calculate the Breakeven Spot Rate
The general procedure involves four steps using a spreadsheet. First, the price is calculated for each model by incorporating current market data and E value into formula (13) and (17). Second, the payoffs for the two models are calculated using a common spot rate and formula 5 and 6. Third, the returns on investment for the two models are calculated and excess return is calculated by subtracting the GK’s return from the PE’s return. Four, using optimizing software, such as Excel’s goal seek or solver, the expiration spot rate is change until the excess return is zero. The resulting spot rate is the breakeven spot rate, . If the PE option is trading at a price different from the price derived using formula (13), the market price is substituted for the formula price in step 1. If the agent wants
. If the PE option is trading at a price different from the price derived using formula (13), the market price is substituted for the formula price in step 1. If the agent wants  for the special case of the two models having the same price, the procedure involves three steps. First, the price is calculated for each model using formula (13) and (17). Second, the difference in prices is calculated. Third, using an optimizing software change the value of the preset exchange rate, E, until the difference in prices is zero. The value of E that equates prices is also the value of
for the special case of the two models having the same price, the procedure involves three steps. First, the price is calculated for each model using formula (13) and (17). Second, the difference in prices is calculated. Third, using an optimizing software change the value of the preset exchange rate, E, until the difference in prices is zero. The value of E that equates prices is also the value of . For the call the PE preferred range is all rates greater than
. For the call the PE preferred range is all rates greater than , while for the put it consists of all rates between the strike rate and
, while for the put it consists of all rates between the strike rate and . The decision whether to buy the PE options is based on whether the agent believes the expiration spot rate will be within the PE preferred range.
. The decision whether to buy the PE options is based on whether the agent believes the expiration spot rate will be within the PE preferred range.
6. Conclusion
In this paper, we present a new foreign exchange option called the Preset Exchange rate option or PE option. In comparison with GK model, the PE model provides the agent with more choices and under some scenarios allows higher returns for higher risks, which are not possible with the GK model. The PE option differs from the conventional GK in three ways. First, it allows the agent to take advantage of a view on both the direction and magnitude of rate movement. Second, it has a provision for an automatic exchange of the payoff at a preset exchange rate, and upon expiration gives the agent the choice of keeping the payoff in the foreign currency or exchanging it back to the pricing currency. Third, at the time of writing, the agent selects the preset exchange rate. The value chosen determines whether the PE option’s price and payoff are equal to, larger, or smaller than the option prices generated from the GK model. We present a decision rule for choosing between buying the PE or the GK options for all values of preset exchange rate as well as a decision rule for the special case where the PE and GK options have the same price. There is a range of spot rates that make the PE option’s return exceed that of the GK option, which we call the PE preferred range. The agent chooses the PE option, if his/her view is that the spot rate at option expiration will be within the preferred range. The preferred range is identified by calculating the spot rate that makes the returns of the two models equal. We call that spot rate the breakeven spot rate. For the call, the PE preferred range consists of all spot rate values greater than the breakeven rate, while for the put, the PE preferred range consists of all spot rate values between the strike rate and breakeven rate. In the special case where the preset exchange rate is set to a value that equates the PE and GK options prices, the preset exchange rate is also the breakeven spot rate. We analyze the impact on the preferred range, of changing the time to expiration, changing spot rate volatility and changing the spread between the foreign and domestic interest rates. As time to expiration is shortened, the call’s PE preferred range widens at a decreasing rate, and the put’s widens at an increasing rate. Likewise, as volatility decreases, the call’s preferred range widens at a decreasing rate, and put’s widens at an increasing rate. As the basis point spread between the foreign and domestic interest rate widens, the preferred ranges of both the call and put widen at a small decreasing rate. Lastly, we present the procedure for the agent to follow when using market data, to calculate the breakeven spot rate and determine the PE preferred range for choosing between the PE and GK options.
REFERENCES
- M. B. Garman and S. W. Kohlhagen, “Foreign Currency Options Values,” Journal of International Money and Finance, Vol. 2, No. 3, 1983, pp. 231-237. doi:10.1016/S0261-5606(83)80001-1
- Bank for International Settlements, “Triennial Central Bank Survey of Foreign Exchange and Derivatives Market Activity,” 1996-2010. http://www.bis.org/publ/rpfxf10t.htm
- F. Black and M. Scholes, “The Valuation of Option Contracts and a Test of Market Efficiency,” Journal of Finance, Vol. 27, No. 2, 1972, pp. 399-417. doi:10.2307/2978484
- F. Black and M. Scholes, “The Pricing of Options and Corporate Liabilities,” Journal of Political Economy, Vol. 81, No. 3, 1973, pp. 637-654. doi:10.1086/260062
- R. C. Merton, “Theory of Rational Option Pricing,” The Bell Journal of Economics and Management Science, Vol. 4, No. 1, 1973, pp. 141-183. doi:10.2307/3003143
- J. Hull and A. White, “The Pricing of Options on Assets with Stochastic Volatilities,” Journal of Finance, Vol. 42, No. 2, 1987, pp. 281-300. doi:10.2307/232853
- J. Hull and A. White, “An Analysis of the Bias in Option Pricing Caused by a Stochastic Volatility,” Journal of International Economics, Vol. 24, No. 4, 1988, pp. 129- 145.
- P. Ritchken and R. Trevor, “Pricing Options under Generalized GARCH and Stochastic Volatilities,” International Journal of Theoretical and Applied Finance, Vol. 59, No. 1, 1999, pp. 377-402. doi:10.1111/0022-1082.00109
- J. B. Wiggins, “Option Values under Stochastic Volatilities,” Journal of Financial Economics, Vol. 19, 1987, pp. 129-145. doi:10.1016/0304-405X(87)90009-2
- S. L. Heston and S. Nandi, “A Closed-Form GARCH Option Valuation Model,” The Review of Financial Studies, Vol. 13, No. 1, 2000, pp. 585-625. doi:10.1093/rfs/13.3.585
- P. Christoffersen, S. Jeston and K. Jacobs, “Option Valuation with Conditional Skewness,” Journal of Econometrics, Vol. 131, No. 1-2, 2006, pp. 253-284. doi:10.1016/j.jeconom.2005.01.010
- L. Mecuri, “Option Pricing in a GARCH Model with Tempered Stable Innovations,” Finance Research Letter, Vol. 5, No. 3, 2008, pp. 172-182. doi:10.1016/j.frl.2008.05.003
- G. Barone-Adesi, H. Rasmussen and C. Ravanelli, “An Option Pricing Formula for the GARCH Diffusion Model,” Computational Statistics and Data Analysis, Vol. 49, No. 2, 2005, pp. 287-310. doi:10.1016/j.csda.2004.05.014
- A. M. Badescu and R. J. Kulperger, “GARCH Option Pricing: A Semi Parametric Approach,” Insurance Mathematics and Economics, Vol. 43, No. 1, 2008, pp. 69-84. doi:10.1016/j.insmatheco.2007.09.011
- H. Gong, A. Thavaneswaran and J. Singh, “A BlackScholes Model with GARCH Volatility,” The Mathematical Scientist, Vol. 35, No. 1, 2010, pp. 37-42.
- H. Gong, A. Thavaneswaran and J. Singh, “Stochastic Volatility Models with Application in Option Pricing,” Journal of Statistical Theory and Practice, Vol. 4, No. 4, 2010, pp. 541-557. doi:10.1080/15598608.2010.10412003
- R. J. Elliot, T. K. Siu and L. Chan, “Option Pricing for GARCH Models with Markov Switching,” International Journal of Theoretical and Applied Finance, Vol. 9. No. 6, 2006, pp. 825-841. doi:10.1142/SO219024906003846
- A. Thavaneswaran, S. Peiris and J. Singh, “Derivation of Kurtosis and Option Pricing Formula for Popular Volatility Models with Applications to Finance,” Communications in Statistics, Theory and Methods, Vol. 37, 2008, pp. 1223-1258. doi:10.1080/03610920701826435
- A. Thavaneswaran, J. Singh and S. S. Appadoo, “Option for Some Stochastic Volatility Models,” Journal of Risk Finance, Vol. 7, No. 4, 2006, pp. 425-445. doi:10.1108/15265940610688982
- E. Pillay and J. G. O’Hara, “FFT Based Option Pricing under a Mean Reverting Process with Stochastic Volatility and Jumps,” Journal of Computation and Applied Mathematics, Vol. 235, No. 12, 2011, pp. 3378-3384. doi:10.1016/j.cam.2010.10.024
- N. Makate and P. Sattayatham, “Stochastic Volatility Jump-Diffusion Model for Option Pricing,” Journal of Mathematical Finance, Vol. 1, No. 3, 2011, pp. 90-97. doi:10.4236/jmf.2011.13012
- S. Pinkham and P. Sattayatha, “European Option Pricing for a Stochastic Volatility Levy Model,” Journal of Mathematical Finance, Vol. 1, No. 2, 2011, pp. 98-108. doi:10.4236/jmf.2011.13013
- H. Gong, A. Thavaneswaran and Y. Liang, “Recent Developments in Option Pricing,” Journal of Mathematical Finance, Vol. 1, No. 3, 2011, pp. 63-71. doi:10.4236/jmf.2011.13009
- V. G. Ivancevic, “Adaptive Wave Models for Sophisticated Option Pricing,” Journal of Mathematic Finance, Vol. 1, No. 3, 2011, pp. 41-49. doi:10.4236/jmf.2011.13006
- C. M. Ahn, D. C. Cho and K. Park, “The Pricing of Foreign Currency Options under Jump-Diffusion Processes,” Journal of Futures Markets, Vol. 27, No. 7, 2007, pp. 669-695.
- I. Hart and M. Ross, “Striking Continuity,” Risk, Vol. 7, No. 6, 1994, pp. 51-56.
NOTES
1Data for the number of contracts from 1997 to 2011 was provided by e-mail on March 20, 2011.
2Data is from Bank of International Settlements website, “Triennial Central Bank Survey of Foreign Exchange and Derivatives Market Activity” reports for 1996-2010 [2].
3Using  and S = 1.00 to calculate the
and S = 1.00 to calculate the  and the percentage change in
and the percentage change in , the 66.7% change in time to expiration causes 2.92% and –4.14% changes in
, the 66.7% change in time to expiration causes 2.92% and –4.14% changes in , which is small.
, which is small.

