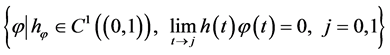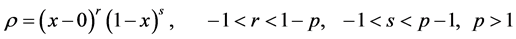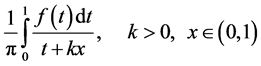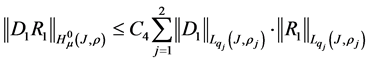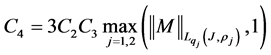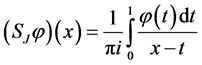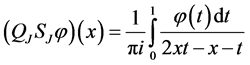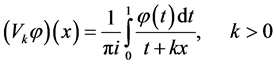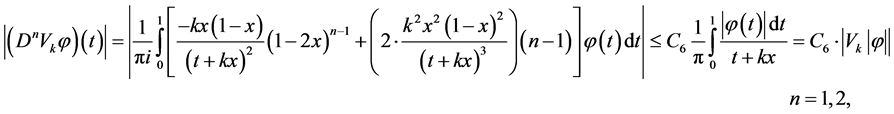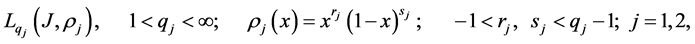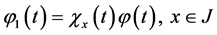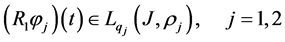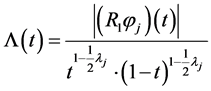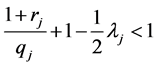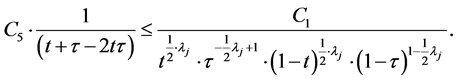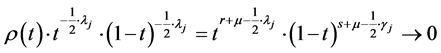Applied Mathematics
Vol.05 No.17(2014), Article ID:50801,6 pages
10.4236/am.2014.517266
Application of Interpolation Inequalities to the Study of Operators with Linear Fractional Endpoint Singularities in Weighted Hölder Spaces
Oleksandr Karelin*, Anna Tarasenko
Institute of Basic Sciences and Engineering, Hidalgo State University, Pachuca, Mexico
Email: *karelin@uaeh.edu.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2014; revised 30 August 2014; accepted 8 September 2014
ABSTRACT
In this paper we consider operators with endpoint singularities generated by linear fractional Carleman shift in weighted Hölder spaces. Such operators play an important role in the study of algebras generated by the operators of singular integration and multiplication by function. For the considered operators, we obtained more precise relations between norms of integral operators with local singularities in weighted Lebesgue spaces and norms in weighted Hölder spaces, making use of previously obtained general results. We prove the boundedness of operators with linear fractional singularities.
Keywords:
Endpoint Singularities, Weighted Holder Space, Weighted Lebesgue Spaces, Relation between Norms, Boundedness

1. Introduction
The solvability theory of singular integral operators has developed independently in Hölder and Lebesgue spaces [1] -[7] , as norms in these spaces differ widely in their structure.
The norm in weighted Hölder spaces is defined in the following way. A function
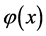 that satisfies the following condition on contour
that satisfies the following condition on contour ,
,
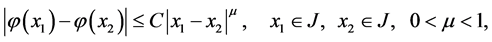
is called Hölder function with exponent
 and constant C on contour J.
and constant C on contour J.
Let J be a power function which has zeros at the endpoints :
:
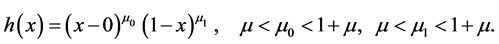
The functions that become Hölder functions and turn into zero at the endpoints, after being multiplied by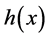 , form a Banach space of Hölder functions with weight h:
, form a Banach space of Hölder functions with weight h:
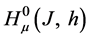 ,
,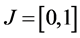 .
.
The norm in space
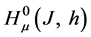 is defined by
is defined by
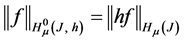
where

and
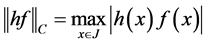 ,
,
 ,
,
specifying that
 .
.
We denote by
 the set of all bounded linear operators mapping the Banach space
the set of all bounded linear operators mapping the Banach space
 into
into
The norm of an operator
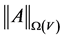
We denote a class of continuous functions on the segment
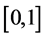
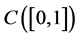
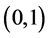
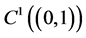
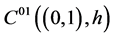
Let us introduce the following notation:
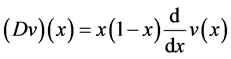
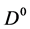
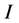
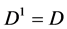
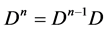
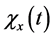
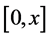
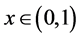
Let

Let
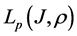
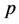
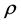
The norm in space
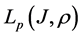
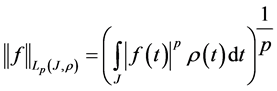
As we can see, the norms in spaces
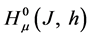
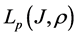
By way of representatives of such types of operators we may consider the following operators with local singularities:
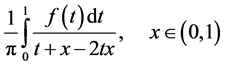
Such operators can be used in the study of boundedness, of belonging of some operators to Banach algebras and of the solvability of operators in weighted Hölder spaces, on the basis of known results for operators in weighted Lebesgue spaces.
2. Inequality Which Connects the Norms in Lebesque and Hölder Weighted Spaces
It is useful to avoid two variables in the second term of the definition of the norm in Hölder spaces, for which we make use of
Lemma 1.
Let
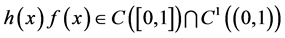
then
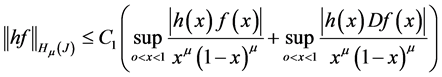
where
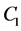
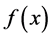
On the basis of Lemma 1 the following theorem can be proved [11] .
Theorem 1.
Let the following conditions hold for some operator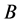
1) Operators
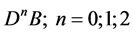
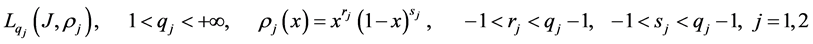
2) For any fixed
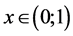
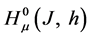
the following properties are fulfilled:
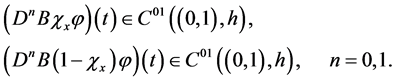
Moreover, inequalities
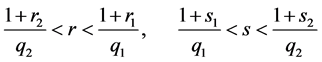
are correct.
It follows that operator
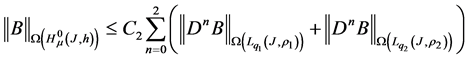
where
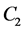
These results can be used in the study of operators in weighted Hölder spaces, on the basis of known results for operators in weighted Lebesgue spaces. In particular, operators with local endpoint singularities can be used in the construction of the left and the right regularizers in the study of Fredholmness of operators in weighted Hölder spaces.
3. Operators with Linear Fractional Endpoint Singularities
We formulate a useful assertion which follows directly from Theorem 1.
Corollary 1. Let properties (1) and (2) be correct for the operator
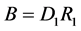
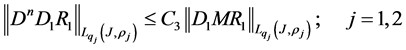
Here
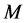
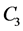
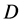
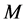
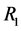
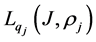
Then
where
We consider the operators
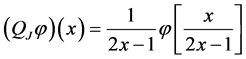
and
We note that for operators

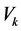
Moreover, the following estimations hold
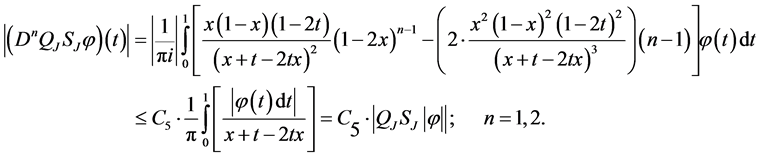
where
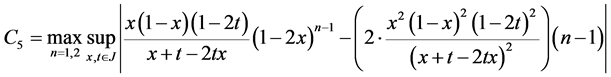
and
where
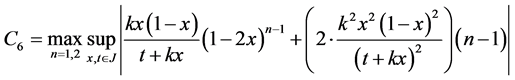
Theorem 2. Let an operator
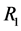
and inequalities (2) be true.
If
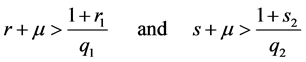
then the operators
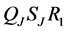

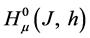
Proof. Let a function
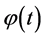
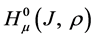
We introduce functions
and
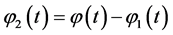
From the fact that
It follows that the function
is summable on segment
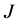
and
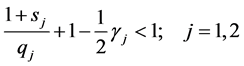
Condition (6) of the theorem makes it possible to choose constants

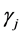
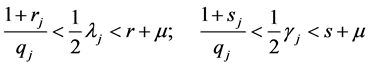
Now, we carry out an estimation of the expression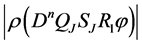
In doing so, we will use inequalities (5),
where
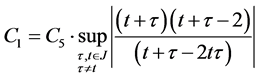
Here we have taken into account that
Since
when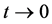

From properties (5), condition (4) follows:
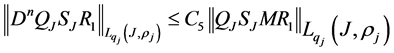
where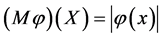
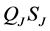
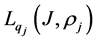
of Corollary 1 are fulfilled and we can apply it. Therefore operator
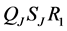
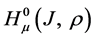
Since operator

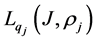
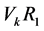
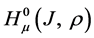
References
- Gakhov, F.D. (1977) Boundary Value Problems. Nauka, Moscow. (in Russian)
- Muskhelishvili, N.I. (2008) Singular Integral Equations, Boundary Value Problems of the Theory of Functions and Some of Their Applications to Mathematical Physics. Dover Publications, Mineola.
- Litvinchuk, G.S. (2000) Solvability Theory of Boundary Value Problems and Singular Integral Equations with Shift. Kluwer Academic Publishers, Dordrecht, Boston, London. http://dx.doi.org/10.1007/978-94-011-4363-9
- Gohberg, I. and Krupnik, N. (1992) One-Dimensional Linear Singular Integral Equations. Operator Theory: Advances and Applications Vol. 53. Birkhauser Verlag, Basel, Boston, Berlin.
- Mikhlin, S.G. and Prossdorf, S. (1986) Singular Integral Operators. Akademie-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-61631-0
- Duduchava, R.V. (1963) Unidimensional Singular Integral Operator Algebras in Spaces of Holder Functions with Weight. Proceedings of A. Razmadze Mathematical Institute, 43, 19-52. (in Russian)
- Karapetiants, N.K. and Samko, S.G. (2001) Equations with Involutive Operator. Birkhauser Verlag, Boston, Basel, Berlin. http://dx.doi.org/10.1007/978-1-4612-0183-0
- Duduchava, R.V. (1979) Convolution Integral Equations with Discontinuous Presymbols, Singular Integral Equations with Fixed Singularities and Their Applications to Problem in Mechanics. Proceedings of A. Razmadze Mathematical Institute, 60, 2-136. (in Russian)
- Karlovich, Yu. and Kravchenko, V. (1981) Singular Integral Equations with Non-Carleman Shift on an Open Contour. Differential Equations, 17, 1408-1417.
- Kravchenko, V.G. and Litvinchuk, G.S. (1994) Introduction to the Theory of Singular Integral Operators with Shift. Kluwer Academic Publishers, Dordrecht, Boston, London. http://dx.doi.org/10.1007/978-94-011-1180-5
- Karelin, A. (1980) On a Boundary Value Problem with Shift for a System of Differential Equations of Elliptichyperbolic Type. Soviet Mathematics-Doklady, 22, 507-512.
NOTES
*Corresponding author.