Regularization Methods to Approximate Solutions of Variational Inequalities

Nguyen Van Kinh

Faculty of Applied Science, Ho Chi Minh City University of Food Industry, Ho Chi Minh City, Vietnam.

DOI: 10.4236/ojop.2023.122004                

Abstract

In this paper, we study the regularization methods to approximate the solutions of the variational inequalities with monotone hemi-continuous operator having perturbed operators arbitrary. Detail, we shall study regularization methods to approximate solutions of following variational inequalities: and with operator A being monotone hemi-continuous form real Banach reflexive X into its dual space X*, but instead of knowing the exact data (y₀, A), we only know its approximate data  satisfying certain specified conditions and D is a nonempty convex closed subset of X; the real function f defined on X is assumed to be lower semi-continuous, convex and is not identical to infinity. At the same time, we will evaluate the convergence rate of the approximate solution. The regularization methods here are different from the previous ones.

Keywords

Ill-Posed Problem, Variational Inequality, Regularization Method, Monotone Operator, Hemi-Continuous Operator, Lower Semi-Continuous Function

1. Introduction

In this paper, we study the regularization methods to approximate the solutions of the following variational inequalities

$\langle Ax-y_0\mathrm{,}x-z\rangle \ge \mathrm{0,}\forall x\in D\mathrm{,}$ (1)

and

$\langle Az-y_0\mathrm{,}x-z\rangle \ge f\left(z\right)-f\left(x\right)\mathrm{,}\forall x\in D\mathrm{,}$ (2)

where A is a hemi-continuous monotone operator form real Banach reflexive X into its dual space $X^{\ast }$ and D is a nonempty convex closed subset of X and $\langle g\mathrm{,}z\rangle$ is the value of the linear functional $g\in X^{\ast }$ at $z\in X$ , i.e. $g\left(z\right)=\langle g\mathrm{,}z\rangle$ . We suppose that (1) or (2) has the exact solutions in D. For the variational inequality (2), the real function f defined on X is assumed to be lower semi-continuous, convex and is not identical to infinity.

These variational inequalities are used in the study of nonlinear problems in physics and engineering, especially in finding solutions to problems in non-linear partial differential equations [1] .

The problem to approximate solutions of variational inequalities (1) or (2) has been posed for a long time, and has been studied by many famous mathematicians in the world, including mathematicians Al’ber Ya. I., Abramov A., Ramm A. G., Riyazantseva P., Browder F. E., Liskovets O. A., who have contributed many foundational works [2] - [19] .

In the 1960s, Browder F. E. was the first to study the problem of finding approximate solutions of (1), (2) and to study the stability of the solutions of these problems by a method that he called the monotone operator method [9] .

After Tikhonov A. N. introduced the variational method, which was later called the Tikhonov regularization method to solve the ill-posed problems in works [20] [21] [22] [23] , Albert Ia. I. was the first to study the stability of the solution of variational inequality (1) according to the Tikhonov regularization method by adding the conjugate operator [4] [5] [6] . Actually, this idea of Browder F. E. has been used in works [9] but has not been prominent in the method.

Liskovevtz O. A. [15] [16] [17] [18] , Nguyen Van Kinh [24] [25] [26] [27] [28] , have achieved many results in this field, especially for variational inequality (1), where the noise operator of the exact operator is non-monotone. However, there are still many unresolved open issues. This paper will address some of these open problems. Detail, we shall study regularization methods to approximate solutions of variational inequalities (1) and (2) with operator A being monotone hemi-continuous form real Banach reflexive X into its dual space $X^{\ast }$ , but instead of knowing the exact data $\left(y_0\mathrm{,}A\right)$ , we only know its approximate data $\left(y_{\delta }\mathrm{,}{A}_h\right)$ satisfying certain specified conditions and D is a nonempty convex closed subset of X.

The paper structure consists of 3 sections: Section 1 the introduction briefly summarizes the recent research results and comes up with problems that need to be studied; Section 2 presents regularization method for variational inequality (1) and Section 3 presents regularization for general variational inequality (2).

2. Regularization Method to Approximate Variational Inequality

First, we give the definition and some properties of topology on non-empty subsets of a topological space, some properties of the variational inequality with the hemi-continuous, monotone operator and dual mapping.

Suppose that X is a topology space. We denote $S\left(X\right)$ as the set of all non-empty subsets of X. We will define a topology on $S\left(X\right)$ as follows:

Definition 2.1 [29] Topology on the set $S\left(X\right)$ that has a basis topology, which is of the form $\left\{M\in S\left(X\right)\mathrm{<mo>\; :\; </mo>}M\subset U\right\}$ , where U is an arbitrary open set of X. This topology is called B-topology on $S\left(X\right)$ . If topology space X is topology defined by metric then B-topology is called β-topology.

The above topological definition can be found in [29] . The following are some characteristics of this topology.

Proposition 2.1 [29] If the sequence of the sets $\left\{M_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ converges to the set $M\subset X$ , denoted by $M_{\sigma }\stackrel{B}{\to }M$ and if the sequence of the sets $\left\{m_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ , with $\varnothing \ne m_{\sigma }\subset M_{\sigma }$ and $M\subset N\subset X$ then $m_{\sigma }\stackrel{B}{\to }N$ .

Proposition 2.2 [29] If the sequence of the sets $\left\{M_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ B-converges to $M\subset X$ , $M\ne \varnothing$ , then arbitrary subsequence of this sequence also B-converges to the set M.

It is easy to see that the sequence of sets $\left\{M_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ B-converges to the set M, which means that for any open set U containing M, then for $\sigma$ “large enough” then $M_{\sigma }\subset U$ . If X is a metric space, then what has just been said is expressed by the following proposition:

Proposition 2.3 [29] Suppose that X is a metric space. Then we have

$M_{\sigma }\stackrel{\beta }{\to }M\iff \beta \left(M_{\sigma }\mathrm{,}M\right)\to \mathrm{0,}$

where $\beta \left(M_{\sigma }\mathrm{,}M\right)=\underset{x\in M_{\sigma }}{\sup }d\left(x\mathrm{,}M\right)=\underset{x\in M_{\sigma }}{\sup }\underset{y\in M}{\inf }d\left(x\mathrm{,}y\right)$ , which is called the deviation of the set $M_{\sigma }$ with respect to the set M.

Proposition 2.4 [29] Suppose that the sequence of sets $\left\{M_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ in Hausdorff topology space X, has the following property:

Taking arbitrarily $x_{\sigma }\in M_{\sigma }$ , we get a sequence of points $\left\{x_{\sigma }\mathrm{,}\sigma \in \Sigma \right\}$ in X. Any subsequence of this sequence has one of the following properties:

1) ${\left\{x_{\phi }\right\}}^{\prime }\cap M\ne \varnothing$ , where ${\left\{x_{\phi }\right\}}^{\prime }$ is the set of limit points of the sequence $\left\{x_{\phi }\right\}$ .

2) $\varnothing \ne {\left\{x_{\phi }\right\}}^{\prime }\subset M$ , where M is a some subset of X.

Then, $M_{\sigma }\stackrel{B}{\to }M$ .

Conversely, if M is a compact set and $M_{\sigma }\stackrel{B}{\to }M$ , then both properties (1) and (2) are true if we replace the set M by the set $\bar{M}$ .

The operator $A\mathrm{<mo>\; :\; </mo>}D\left(A\right)\subset X\to X^{\ast }$ is called monotone if it satisfies the following condition

$\langle Ax-Ay\mathrm{,}x-y\rangle \ge \mathrm{0,}\forall x\mathrm{,}y\in D\left(A\right)\mathrm{.}$ (3)

The operator A is called strictly monotone if (3) with an equals sign occurs if and only if $x=y$ .

The operator A is called hemi-continuous at $x_0\in D\left(A\right)$ if for any x such that:

$\begin{array}{l}{x}_0+tx\in D\left(A\right)\mathrm{,}\forall t\in \left(\mathrm{0,}\alpha \right]\mathrm{,}\alpha =\alpha \left(x\right)>0\text{and}\forall \left\{t_n\right\}\mathrm{,}{t}_n\in \left(\mathrm{0,}\alpha \right]\mathrm{,}{t}_n\to 0\\ \Rightarrow A\left(x_0+t_{n}x\right)\rightharpoonup A\left(x_0\right)\mathrm{,}\text{as}n\to \infty \mathrm{.}\end{array}$

A is called hemi-continuous on $D\left(A\right)$ if it is continuous at every point $x\in D\left(A\right)$ .

An extension of Minty’s Lemma is that the following variational inequalities are equivalent:

Lemma 2.1 [29] If $A\mathrm{<mo>\; :\; </mo>}D\left(A\right)\subset X\to X^{\ast }$ is a monotone and hemi-continuous, then the following variational inequalities are equivalent, i.e., they have the same of the solution sets:

$\langle Ax-y\mathrm{,}x-z\rangle \ge \epsilon \Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{,}$ (4)

$\langle Az-y\mathrm{,}x-z\rangle \ge \epsilon \Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{,}$ (5)

where $\epsilon >0$ and D is convex closed subset of $D\left(A\right)$ .

Lemma 2.2 Let $g\left(t\right)$ be a non-negative real, continuous, and $B\mathrm{<mo>\; :\; </mo>}D\left(B\right)\subset X\to X^{\ast }$ be a hemi-continuous at $z\in D\left(B\right)$ , $D\left(B\right)$ be a convex subset of X and $\epsilon >0$ . If

$\langle Bx-y\mathrm{,}x-z\rangle \ge \epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\left(B\right)$ (6)

then

$\langle Bz-y\mathrm{,}x-z\rangle \ge \epsilon g\left(\Vert z\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\left(B\right)$ (7)

Proof. Suppose that $z\in D\left(B\right)$ satisfies (6). Let $\omega \in D\left(B\right)$ , then $m=tz+\left(1-t\right)\omega \in D\left(B\right)$ , with $0<t<1$ , because $D\left(B\right)$ is convex and $z\mathrm{,}\omega \in D\left(B\right)$ .

By replacing x in the variational inequality (6) by m, we obtain

$\langle Bm-y\mathrm{,}m-z\rangle \ge \epsilon g\left(\Vert m\Vert \right)\Vert m-z\Vert \mathrm{,}\forall \omega \in D(\; B\; )$

or

$\left(1-t\right)\langle Bm-y\mathrm{,}\omega -z\rangle \ge \epsilon \left(1-t\right)g\left(\Vert m\Vert \right)\Vert m-z\Vert \mathrm{,}\forall z\mathrm{,}\omega \in D\left(B\right)\mathrm{.}$

Therefore

$\langle Bm-y\mathrm{,}\omega -z\rangle \ge \epsilon g\left(\Vert tz+\left(1-t\right)\omega \Vert \right)\Vert \omega -z\Vert \mathrm{,}\forall z\mathrm{,}\omega \in D\left(B\right)$ (8)

Since $g\left(t\right)$ is a continuous function, then $g\left(\Vert tz+\left(1-t\right)\omega \Vert \right)\to g\left(\Vert z\Vert \right)$ as $t\to 1$ and since B is hemi-continuous at z, then the left hand side of (8) converges to $\langle Bz-y\mathrm{,}\omega -z\rangle$ as $t\to 1$ . Therefore, we have

$\langle Bz-y\mathrm{,}x-z\rangle \ge \epsilon g\left(\Vert z\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\left(B\right)\mathrm{.}$

Lemma is proved.

The mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is called dual mapping of the norm space X if it satisfies the following conditions

$\Vert Ux\Vert =\Vert x\Vert ,\langle Ux,x\rangle =\Vert Ux\Vert \Vert x\Vert ={\Vert x\Vert }^2,\forall x\in X.$

This concept was first studied by Browder F. E. [8] and Vaiberg M. M. [30] .

The norm space X is called strictly convex if it has the following property

$\Vert x+y\Vert =\Vert x\Vert +\Vert y\Vert \mathrm{,}x\mathrm{,}y\in X\Rightarrow \left\{x\mathrm{,}y\right\}\text{is}\text{linearly}\text{dependent}\text{.}$

Next, we state some properties of duality mapping, which are used in the following sections.

Proposition 2.5 [30] The dual mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is single if dual space $X^{\ast }$ is strictly convex.

The mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is called coercive if

$\langle Ux\mathrm{,}x\rangle \ge c\left(\Vert x\Vert \right)\Vert x\Vert \mathrm{,}\forall x\in X\mathrm{,}$

where $c\left(t\right)$ is a non-negative real function and $c\left(t\right)\to +\infty$ as $t\to +\infty$ .

Proposition 2.6 [30] The dual mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is coercive, monotone. Moreover, if X is a strictly convex space then U is strictly monotone.

Proposition 2.7 [30] If X is a reflexive real space and its dual space is strictly convex then the dual mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is hemi-continuous.

From the definition of the dual mapping, it follows that

$\langle Ux-Uy\mathrm{,}x-y\rangle \ge {\left(\Vert x\Vert -\Vert y\Vert \right)}^2\mathrm{,}\forall x\mathrm{,}y\in X\mathrm{.}$

Now we begin to present the regularization method to approximate solution of the variational inequality (1).

In the section, we assume that is a real reflective Banach space X with the conjugate space $X^{\ast }$ being strictly convex. Then, the dual mapping $U\mathrm{<mo>\; :\; </mo>}X\to X^{\ast }$ is single, coercive, monotone and hemi-continuous (Proposition 2.5, Proposition 2.6, Proposition 2.7).

As we already know the problem of finding the solution of the variational inequalities (1) is generally an ill-posed problem. Therefore, it is necessary to study some variational methods solving such problems to ensure that the solutions are stable, i.e. the solutions depend continuously on small changes to the exact data. We will present the regularization method with small parameter to approximate the variational inequality (1).

Suppose with exact data $\left(y_0\mathrm{,}A\right)$ , the solution set of the variational inequality (1) is $Z_0\ne \varnothing$ . Since A is a hemi-continuous monotone operator from real Banach reflexive X into its dual space $X^{\ast }$ and D is a nonempty convex closed subset of X, then $Z_0$ is a convex, closed set [30] . Instead of knowing the exact data $\left(y_0\mathrm{,}A\right)$ , we only know its approximate data $\left(y_{\delta }\mathrm{,}{A}_h\right)$ satisfying the following conditions

$\Vert y_{\delta }-y_0\Vert \le \delta \mathrm{,}$ (9)

and

$\Vert A_{h}x-Ax\Vert \le hg\left(\Vert x\Vert \right)\mathrm{,}\forall x\in D\left(A_h\right)\mathrm{,}$ (10)

where the operator $A_h\mathrm{<mo>\; :\; </mo>}D\left(A_h\right)\subset X\to X^{\ast }$ , $D\left(A_h\right)=D\left(A\right)=D\subset X$ , $A_h$ is an arbitrary operator, not necessarily monotone or hemi-continuous, and the real function $g\left(t\right)$ is non-negative, continuous and increasing no faster than some linear function, i.e., there exist $M\ge \mathrm{0,}N\ge 0$ such that

$g\left(t\right)\le Mt+N\mathrm{,}\forall t\ge 0.$ (11)

In this work, we construct an approximate solution of (1), according to the regularization method, is the solutions of the variational inequality

$\langle A_{h}x+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{,}$ (12)

where $\epsilon \ge 0$ is a small parameter.

Remark 2.1

1) If the operator $A_h$ is non-monotone, non-hemicontinuous then in [17] , Liskovets O. A. studied the Tikhonov regularization solution of (1) which is the solution of (12) with $g\left(t\right)\equiv 1$ , i.e., the solution of the variational inequality:

$\langle A_{h}x+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge -\epsilon \Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (13)

2) If the operator $A_h$ is non-monotone, non-hemicontinuous, then in [18] , Liskovets O. A. studied the approximate solution of (1) which is the solution of the variational inequality:

$\langle A_{h}z+\alpha Uz-y_{\delta }\mathrm{,}x-z\rangle \ge -\epsilon g\left(\Vert z\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (14)

Since the operator $A_h$ is arbitrary, the two sets of solutions for (12) and (14) are different, so the author’s and [18] ’s methods are different. The following example demonstrates it:

Let $X=ℝ$ be real normal space, therefore, its conjugate space also be $ℝ$ and its dual mapping U be identity mapping. Let $D=\left[-1,1\right]$ , $y_0=0$ .

Suppose that the exact operator $A\mathrm{<mo>\; :\; </mo>}D\to ℝ$ , is defined by

$Ax=\{\begin{array}{l}x+1,-1\le x<0\\ 1,0\le x\le 1\end{array}$

Clearly the operator A is monotone and hemi-continuous on D.

The approximate operator $A_h$ of the operator A is defined by

$A_{h}x=\{\begin{array}{l}x+1,-1\le x<0\\ 1+h,x=0\\ 1,0<x\le 1\end{array}$

Therefore, the operator $A_h$ is non-monotone, non-hemicontinuous on D and

$\Vert A_{h}x-Ax\Vert \le h\mathrm{,}\forall x\in D\mathrm{.}$

Let $g\left(t\right)\equiv 1,0<\epsilon -h<1,\epsilon <1$ . Therefore, the variational inequality (12) has the form

$\langle A_{h}x+\alpha x,x-0\rangle =\left(A_{h}x+\alpha x\right)x\ge -\epsilon \left|x-0\right|,\forall x\in D=\left[-1,1\right].$

Consequently, $z=0$ is the solution of the variational inequality (12).

On the other hand, the following inequality is not true

$\left(1+h\right)x\ge -\epsilon \left|x\right|\mathrm{,}\forall x\in \left[-\mathrm{1,1}\right]\mathrm{.}$

So $z=0$ is not the solution of the variational inequality (14).

Therefore, the solution sets of (12) and (14) are different.

In the following, we study the existence of an approximate solution and the stability of the solution of the regualaiation method (12).

We denote the solution set of (12) as $Z_{\Delta }^{\alpha }$ , where $\Delta =\left(h\mathrm{,}\epsilon \mathrm{,}\delta \right)$ . The following theorem asserts the existence of a solution of (12), that is, the existence of the Tikhonov regularization operator.

Theorem 2.1 If $\epsilon \ge h$ , then $Z_{\Delta }^{\alpha }\ne \varnothing$ .

Proof. We consider the following variational inequality

$\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge \mathrm{0,}\forall x\in D\mathrm{.}$ (15)

By assumption, the operators A and U are single, monotone, hemicontinuous, so $A+\alpha U$ is also single, monotone, hemicontinuous.

+ If D is non-bounded, then the operator $A+\alpha U$ is coercive on D. Indeed, we have

$\begin{array}{c}\frac{\langle Ax+\alpha Ux\mathrm{,}x-x_0\rangle }{\Vert x\Vert }=\frac{\langle Ax-A{x}_0\mathrm{,}x-x_0\rangle }{\Vert x\Vert }+\frac{\langle A{x}_0\mathrm{,}x-x_0\rangle }{\Vert x\Vert }+\alpha \frac{\langle Ux\mathrm{,}x-x_0\rangle }{\Vert x\Vert }\\ \ge -\frac{\Vert A{x}_0\Vert \Vert x-x_0\Vert }{\Vert x\Vert }+\alpha \frac{\langle Ux\mathrm{,}x\rangle }{\Vert x\Vert }-\alpha \frac{\langle Ux\mathrm{,}{x}_0\rangle }{\Vert x\Vert }\\ \ge -\frac{\Vert A{x}_0\Vert \Vert x-x_0\Vert }{\Vert x\Vert }+\alpha \frac{{\Vert x\Vert }^2}{\Vert x\Vert }-\alpha \frac{\Vert x\Vert \Vert x_0\Vert }{\Vert x\Vert }\\ =-\frac{\Vert A{x}_0\Vert \Vert x-x_0\Vert }{\Vert x\Vert }+\alpha \Vert x\Vert -\alpha \Vert x_0\Vert \mathrm{.}\end{array}$

Therefore, if $x\in D\mathrm{,}\Vert x\Vert \to +\infty$ then $\frac{\langle Ax+\alpha Ux\mathrm{,}x-x_0\rangle }{\Vert x\Vert }\to +\infty$

So, the operator is coercive on D.

Since $A+\alpha U$ is monotone, hemi-continuous, coercive, according to [8] [31] the variational inequality (15) has a solution in D.

+ If D is bounded, according to [32] , the variational inequality (15) has a solution in D.

We will show that the solutions of (15) are all solutions of (12). Indeed, taking $z\in D$ as an arbitrary solution of (15), we have

$\begin{array}{c}\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle =\langle A_{h}x-Ax+Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \\ =\langle A_{h}x-Ax\mathrm{,}x-z\rangle +\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \mathrm{.}\end{array}$

Since $z\in D$ is the solution (15) then

$\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge \mathrm{0,}\forall x\in D\mathrm{.}$

Consequently,

$\begin{array}{c}\langle Ax+\alpha Ux-y_{\delta },x-z\rangle \ge \langle A_{h}x-Ax,x-z\rangle \\ \ge -\Vert A_{h}x-Ax\Vert \Vert x-z\Vert \\ \ge -hg\left(\Vert x\Vert \right)\Vert x-z\Vert \\ \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert ,\left(\epsilon >h\right).\end{array}$

So, $z\in Z_{\Delta }^{\alpha }$ .

Theorem is proved.

Theorem 2.2 If $\epsilon \ge h$ and $M\frac{h+\epsilon }{\alpha }<k_1<1$ , $\frac{\delta }{\alpha }<k_2<+\infty$ , where $k_1\mathrm{,}{k}_2$ are constants, $Z_{\Delta }^{\alpha }$ is the set of the solution of (12) then the sequence of the sets $Z_{\Delta }^{\alpha }$ is uniformly bounded in X.

Proof. By assumption $\epsilon \ge h$ and by Theorem 2.1. then $Z_{\Delta }^{\alpha }\ne \varnothing$ . Let $z\in Z_{\Delta }^{\alpha }$ , we have

$\langle A_{h}x+\alpha Uz-y_{\delta }\mathrm{,}x-z\rangle \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D$

or

$\langle A_{h}x-Ax\mathrm{,}x-z\rangle +\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D$

$\Rightarrow \langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge -\langle A_{h}x-Ax\mathrm{,}x-z\rangle -\epsilon g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D$

Consequently

$\langle Ax+\alpha Ux-y_{\delta }\mathrm{,}x-z\rangle \ge -\left(h+\epsilon \right)g\left(\Vert x\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (16)

Since the operator is monotone, hemi-continuous and Lemma 2.2, from (16) it follows that

$\langle Az+\alpha Uz-y_{\delta }\mathrm{,}x-z\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z\Vert \right)\Vert x-z\Vert \mathrm{,}\forall x\in D$

or

$\langle Az-y_0\mathrm{,}x-z\rangle +\langle y_0-y_{\delta }\mathrm{,}x-z\rangle +\left(h+\epsilon \right)g\left(\Vert z\Vert \right)\Vert x-z\Vert \ge \alpha \langle Uz\mathrm{,}z-x\rangle \mathrm{.}$

So

$\begin{array}{l}\langle Az-y_0\mathrm{,}x-z\rangle +\left[\delta +\mathrm{<mo\; stretchy="false">\; (\; </mo>}h+\epsilon \mathrm{<mo\; stretchy="false">\; )\; </mo>}g\left(\Vert z\Vert \right)\right]\Vert x-z\Vert \\ \ge \alpha \langle Uz\mathrm{,}z-x\rangle =\alpha \Vert z\Vert \Vert z-x\Vert \mathrm{,}\forall x\in D\mathrm{.}\end{array}$ (17)

In (17) we take $x=x_0\in Z_0\subset D$ , with $x_0$ is the solution of (1), we have

$\langle Az-y_0\mathrm{,}{x}_0-z\rangle \le \mathrm{0,}\forall z\in Z_{\Delta }^{\alpha }\mathrm{.}$

Consequently

$\left[\delta +\left(h+\epsilon \right)g\left(\Vert z\Vert \right)\right]\Vert x_0-z\Vert \ge \alpha {\Vert z\Vert }^2-\alpha \Vert x_0\Vert \Vert z\Vert \mathrm{,}\forall z\in Z_{\Delta }^{\alpha }\mathrm{.}$ (18)

Since $g\left(t\right)\le Mt+N\mathrm{,}\forall t\ge 0$ , then from (18) it follows that

$\begin{array}{l}\left[M\frac{h+\epsilon }{\alpha }-1\right]{\Vert z\Vert }^2+\left[\frac{\delta }{\alpha }+M\frac{h+\epsilon }{\alpha }\Vert x_0\Vert +N\frac{h+\epsilon }{\alpha }\Vert x_0\Vert \right]\Vert z\Vert \\ +N\frac{h+\epsilon }{\alpha }\Vert x_0\Vert \ge 0,\forall z\in Z_{\Delta }^{\alpha }.\end{array}$ (19)

By assumption $M\frac{h+\epsilon }{\alpha }-1<0$ , $\frac{\delta }{\alpha }<k_2<+\infty$ , and (19) is a quadratic inequality in terms of $\Vert z\Vert$ , then the set of $\Vert z\Vert$ in (19) is bounded. Since $k_1\mathrm{,}{k}_2$ are constants which do not depend on $h\mathrm{,}\epsilon \mathrm{,}\delta \mathrm{,}\alpha$ , then the sequence of the sets $Z_{\Delta }^{\alpha }$ is uniformly bounded, i.e., there exists a constant k which do not depend on $h\mathrm{,}\epsilon \mathrm{,}\delta \mathrm{,}\alpha$ such that

$\Vert z\Vert \le k,\forall z\in Z_{\Delta }^{\alpha },\forall \Delta =\left(h,\epsilon ,\delta \right),\forall \alpha .$

Theorem is proved.

Remark 2.2

1) If $\frac{h+\epsilon +\delta }{\alpha }$ is uniformly bounded then the sequence of sets $Z_{\Delta }^{\alpha }$ , with $Z_{\Delta }^{\alpha }$ being the set of the solutions of (13), is uniformly bounded [18] .

2) The conditions for the sequence of sets $Z_{\Delta }^{\alpha }$ , with $Z_{\Delta }^{\alpha }$ being the set of the solutions of (14), is uniformly bounded , which is the same as theorem above [17] .

3) Instead of regularization for the solution of the variational inequality (1), we regulate for the solution of the equation $Ax=y_0$ , where A is given exactly and $y_{\delta }$ is an approximation of $y_0$ satisfying (9), in [3] [4] the condition is uniformly bounded the sequence of solution sets of (13) with $A_h$ replaced by A, is $\frac{\delta }{\alpha }<k$ , with k constant.

The following theorems talk about the stability of the solution of the variational inequality (1) according to the Tikhonov regularization method.

Theorem 2.3 With the same assumptions as in Theorem 2.2, the sequence of the sets $Z_{\Delta }^{\alpha }$ , B-weakly converges to exactly solution set $Z_0$ of the variational inequality (1) as $\alpha \to 0$ .

Proof. Let arbitrary $z_{\Delta }^{\alpha }\in Z_{\Delta }^{\alpha }$ , from Theorem 2.2 it follows that the sequence $\left\{z_{\Delta }^{\alpha }\right\}$ is uniformly bounded. Since X is a reflexive space and $\left\{z_{\Delta }^{\alpha }\right\}\subset X$ , there exists a subsequence $\left\{z_{\Delta }^{\beta }\right\}$ of the sequence such that it weakly converges to $z_{\ast }\in D$ (since $z_{\Delta }^{\beta }\in D$ and D is weakly closed). We shall denote $z_{\Delta }^{\beta }\rightharpoonup z_{\ast }\in D$ .

Since $z_{\Delta }^{\beta }$ is the solution of (12), we have

$\langle A_{h}x+\alpha Ux-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (20)

The argument is the same as in the proof of Theorem 2.2, using Lemma 2.2, from (20) it follows that

$\langle A{z}_{\Delta }^{\beta }+\beta U{z}_{\Delta }^{\beta }-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (21)

Since the operator $A+\beta U$ is monotone, from (21) it follows that

$\langle Ax+\beta Ux-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (22)

Since the function $g\left(t\right)$ is continuous and the sequence $\left\{z_{\Delta }^{\beta }\right\}$ is bounded, the sequence $\left\{g\Vert z_{\Delta }^{\beta }\Vert \right\}$ is bounded. Therefore, in (22) taking $\beta \to 0$ , therefore, $\delta \to 0$ , we have

$\langle Ax-y_0\mathrm{,}x-z_{\ast }\rangle \ge \mathrm{0,}x\in D\mathrm{.}$

Consequently, $z_{\ast }\in Z_0$ .

From this, according to Proposition 2.4, it follows that the sequence of the sets $\left\{Z_{\Delta }^{\alpha }\right\}$ B-weakly converges to exactly solution set $Z_0$ of the variational inequality (1) as $\alpha \to 0$ .

Theorem is proved.

We denote

$Z_{\ast }:=\arg \underset{z\in Z_0}{\min }\left\{\Vert z\Vert \right\}=\left\{z:\Vert z\Vert =\underset{z\in Z_0}{\min }\Vert u\Vert \right\}.$

Since X is a reflexive real Banach space and $Z_0$ is a closed convex subset in X, then $Z_{\ast }\ne \varnothing$ .

Theorem 2.4 The sequence of the sets $\left\{Z_{\Delta }^{\alpha }\right\}$ B-weakly converges to $Z_{\ast }$ as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ . Moreover, let arbitrary $z_{\Delta }^{\alpha }\in Z_{\Delta }^{\alpha }$ and $z_{\ast }\in Z_{\ast }$ then

$\Vert z_{\Delta }^{\alpha }\Vert \to \Vert z_{\ast }\Vert \mathrm{,}\text{as}\alpha \to \mathrm{0,}\frac{h+\epsilon +\delta }{\alpha }\to 0.$

Proof. + We first prove $z_{\Delta }^{\alpha }\rightharpoonup z_{\ast }$ as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

Since $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ , then we take $\alpha \mathrm{,}\frac{h+\epsilon +\delta }{\alpha }$ is small enough such that

$\epsilon \ge h,M\frac{h+\epsilon }{\alpha }<k_1<1,\frac{\delta }{\alpha }<k_2<+\infty$ (23)

Therefore, let arbitrary $z_{\Delta }^{\alpha }\in Z_{\Delta }^{\alpha }$ , then the sequence $\left\{z_{\Delta }^{\alpha }\right\}$ is uniformly bounded (Theorem 2.2). Since X is a reflexive space and $\left\{z_{\Delta }^{\alpha }\right\}\subset X$ , there exists a subsequence $\left\{z_{\Delta }^{\beta }\right\}$ of the sequence such that $z_{\Delta }^{\beta }\rightharpoonup z_{\ast }\in D$ (since $z_{\Delta }^{\beta }\in D$ and D is weakly closed) as $\beta \to 0$ , $\frac{h+\epsilon +\delta }{\beta }\to 0$ . The argument is the same as in the proof of Theorem 2.3, we have $z_{\ast }\in Z_{\ast }$ .

Since $z_{\Delta }^{\beta }$ is a solution of (12), we have

$\langle A_{h}x+\beta Ux-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\epsilon g\left(\Vert x\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$

From the above inequalities, it follows that

$\langle Ax+\beta Ux-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert x\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$

From the above inequality, according to Lemma 2.2, it follows that

$\langle A{z}_{\Delta }^{\beta }+\beta U{z}_{\Delta }^{\beta }-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$ (24)

Since the operator $A+\beta U$ is monotone, from (24) it follows that

$\langle Ax+\beta Ux-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$

or

$\begin{array}{l}\langle Ax-y_0\mathrm{,}x-z_{\Delta }^{\beta }\rangle +\langle y_0-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle +\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \\ \ge \beta \langle Ux\mathrm{,}{z}_{\Delta }^{\beta }\rangle \mathrm{,}\forall x\in D\mathrm{.}\end{array}$ (25)

In (25), taking $x\in Z_0\subset D$ , we have

$\langle Ax-y_0\mathrm{,}x-z_{\Delta }^{\beta }\rangle \le 0$

Hence, from (25) it follows that

$\delta \Vert x-z_{\Delta }^{\beta }\Vert +\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \ge \beta \langle Ux\mathrm{,}{z}_{\Delta }^{\beta }\rangle \mathrm{,}\forall x\in Z_0\mathrm{.}$ (26)

Since sequence $\left\{z_{\Delta }^{\beta }\right\}$ is bounded and $g\left(t\right)$ is continuous, in (26) taking $\beta \to 0$ , $\frac{h+\epsilon +\delta }{\beta }\to 0$ , we obtain

$\langle Ux\mathrm{,}{z}_{\ast }-x\rangle \le \mathrm{0,}x\in Z_0\mathrm{.}$ (27)

From (27), according to Lemma of Minty, it follows that

$\langle U{z}_{\ast }\mathrm{,}{z}_{\ast }-x\rangle \le \mathrm{0,}x\in Z_0\mathrm{.}$ (28)

Due to the property of the dual mapping U, from (28) it follows that

${\Vert z_{\ast }\Vert }^2\le \langle U{z}_{\ast }\mathrm{,}x\rangle \le \Vert z_{\ast }\Vert \Vert x\Vert \mathrm{,}\forall x\in Z_0\mathrm{.}$

Hence

$\Vert z_{\ast }\Vert \le \Vert x\Vert \mathrm{,}\forall x\in Z_0\mathrm{.}$

Consequently,

$z_{\ast }\in Z_{\ast }\mathrm{.}$

Therefore, the sequence of sets $\left\{Z_{\Delta }^{\alpha }\right\}$ B- weakly converges to $Z_{\ast }$ as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

+ Next, we prove $\Vert z_{\Delta }^{\alpha }\Vert \to \Vert z_{\ast }\Vert$ , as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

Since the operator A is monotone, from (24) it follows that

$\langle A{z}_{\Delta }^{\beta }+\beta U{z}_{\Delta }^{\beta }-y_{\delta }\mathrm{,}x-z_{\Delta }^{\beta }\rangle \ge -\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \mathrm{,}\forall x\in D\mathrm{.}$

The argument is the same as in the above proof and from the above inequality, we have

$\delta \Vert x-z_{\Delta }^{\beta }\Vert +\left(h+\epsilon \right)g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \ge \beta \langle U{z}_{\Delta }^{\beta }\mathrm{,}{z}_{\Delta }^{\beta }-x\rangle \mathrm{,}\forall x\in Z_0\mathrm{,}$

or

$\frac{\delta }{\beta }\Vert x-z_{\Delta }^{\beta }\Vert +\frac{h+\epsilon }{\beta }g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert x-z_{\Delta }^{\beta }\Vert \ge \langle U{z}_{\Delta }^{\beta }\mathrm{,}{z}_{\Delta }^{\beta }-x\rangle \mathrm{,}\forall x\in Z_0\mathrm{.}$ (29)

In (29), replacing x by $z_{\ast }$ , we have

$\langle U{z}_{\Delta }^{\beta }\mathrm{,}{z}_{\Delta }^{\beta }-z_{\ast }\rangle \le \frac{\delta }{\beta }\Vert z_{\ast }-z_{\Delta }^{\beta }\Vert +\frac{h+\epsilon }{\beta }g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert z_{\ast }-z_{\Delta }^{\beta }\Vert \mathrm{.}$ (30)

According to the property of the dual mapping U, from (30) it follows that

${\left(\Vert z_{\ast }\Vert -\Vert z_{\Delta }^{\beta }\Vert \right)}^2\le \langle U{z}_{\ast }-U{z}_{\Delta }^{\beta }\mathrm{,}{z}_{\ast }-z_{\Delta }^{\beta }\rangle =\langle U{z}_{\ast }\mathrm{,}{z}_{\ast }-z_{\Delta }^{\beta }\rangle +\langle U{z}_{\Delta }^{\beta }\mathrm{,}{z}_{\ast }-z_{\Delta }^{\beta }\rangle \mathrm{.}$

${\left(\Vert z_{\ast }\Vert -\Vert z_{\Delta }^{\beta }\Vert \right)}^2\le \langle U{z}_{\ast }\mathrm{,}{z}_{\ast }-z_{\Delta }^{\beta }\rangle +\frac{\delta }{\beta }\Vert z_{\ast }-z_{\Delta }^{\beta }\Vert +\frac{h+\epsilon }{\beta }g\left(\Vert z_{\Delta }^{\beta }\Vert \right)\Vert z_{\ast }-z_{\Delta }^{\beta }\Vert$ (31)

In (31), taking $\beta \to 0$ , $\frac{h+\epsilon +\delta }{\beta }\to 0$ , we obtain $\Vert z_{\Delta }^{\beta }\Vert \to \Vert z_{\ast }\Vert \mathrm{.}$

The above happens for every subsequence $\left\{\Vert z_{\Delta }^{\beta }\Vert \right\}$ of the sequence $\Vert z_{\Delta }^{\alpha }\Vert$ , so the sequence itself also converges to $\Vert z_{\ast }\Vert$ as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

Theorem is proved.

Corollary 2.1 If X is a E-space [33] , then $\left\{Z_{\Delta }^{\alpha }\right\}$ B-converges to $Z_{\ast }$ as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

Proof. It follows from Theorem 2.4.

Corollary 2.2 Suppose that X is a E-space and the set $Z_{\ast }$ has only one element (this happens, for example, A is a stricly monotone operator and X is a strictly convex space). Therefore, if $z_{\Delta }^{\alpha }$ arbitrarily in $Z_{\Delta }^{\alpha }$ , then $z_{\Delta }^{\alpha }\to z_{\ast }$ , as $\alpha \to 0$ , $\frac{h+\epsilon +\delta }{\alpha }\to 0$ .

Proof. It follows from Theorem 2.4.

If we don’t know if (1) has a solution before, then the following theorem tells us that.

Theorem 2.5 The necessary and sufficient condition for the variational inequality (1) to have a solution is that the sequence of sets $\left\{Z_{\Delta }^{\alpha }\right\}$ B-weakly converges to some unique bounded subset of X as,.

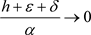Proof. Suppose that the sequence of sets 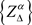B-weakly converges to bounded subset as,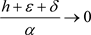. Since X is a reflexive Banach space and by Proposition 2.1, without loss of generality, we can assume that Z is a weakly compact set.

Let arbitrary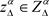, then there exists the subsequence of the sequence such that as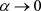, (by Proposition 2.4). The argument is the same as in the proof of Theorem 2.3, it follows that satisfies

Hence, 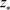is a solution of (1).

Conversely, if, then from Theorem 2.4, it follows that the sequence of sets 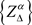B- weakly converges to bounded subset as.

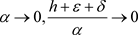Theorem is proved.

We now present an example where the above regularization method can be applied. This example is slightly modified in [18] [30] .

As usual, the notation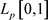, , 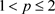is the normed space of real functions p-integrable in the Lebesgue sense on the interval [0,1]. As we all know, is a reflecxive Banach space, and its conjugate space is, with, is strictly convex.

Let be a non-negative real function, continuous on the variable on the unit square and is also a definite and continuous real function on the unit square, without decreasing according to the variable t and satisfies the condition

where is a continuous, non-negative real function on, and b is a positive constant.

The operator A is defined as:

(32)

According to [30] , this operator acts from to, with the domain

Operator A is monotone. Indeed, let, we have

Since the function is not negative and is not decrease respect to the variable t, the right hand side of the above inequality is non-negative. So,

According to [30] the operator hemi-continuous.

The perturbed operator of A is defined as follows

(33)

where is a measurable real function on the unit square as follows

(34)

and is also a measurable real function on the unit square as follows

(35)

with is a non negative real function in.

According to [30] , from (34), (35) it follows that acts from to, with the domain.

Clearly, in general, is not monotone and not continuous. Moreover, after calculating and estimating, we have

(36)

where

Since, then.

By using the inequality

we have an estimate of the function g as follows:

where, and.

We have g is continuous and

Therefore, we can apply the above regularization method to find the approximate solution of the variational inequality (1) with the operator A is given by (32) and its perturbed operator is given by (33).

3. Regularizer of General Variational Inequality

3.1. Regularization Method Solving the General Variational Inequality-Strong Stability

In this subsection, we consider X to be a real reflexive space and satisfies the following conditions:

1) There exists a mapping U from X to the conjugate space, which maps the bounded subsets of X to the bounded subset of;

2) For every fixed that belongs to X, then, as (this condition is often called U as satisfying the coercive condition);

3) For every bounded sequence and such that:

Remark 3.1 If X is a uniformly convex space and the conjugate space is a strictly convex space, then the dual mapping satisfies the above conditions [30] .

We consider the following variational inequality

(37)

where A is a monotone, hemi-continuous, acting from X into, with domain, , , is lower semi-continuous and D is a convex closed subset of.

As we know the solution of (37) is which satisfies (37). The class of problems of the form (37) is often called the general variational inequalities. This class of problems contains special cases: the first kind operator equations, where A is a monotonous operator; variational inequality problems on convex sets with monotone operators on convex sets.

If then we have studied in the Section 2.

The existence of solutions of (37) has been studied by Browder F. E. and many other mathematicians in the world, some typical works can be mentioned as [10] [11] [34] .

For the first time, the author studies the approximate solution of the variational inequality (37) by the Tikhonov regularization method [24] [25] [26] [27] [28] , as follows:

Assume that for exact data the exact solution set of (37) is. In fact, instead of knowing this exact data, we only know its approximate data that satisfies the conditions

(38)

and

(39)

where, is not necessarily a monotone operator or hemi-continuous.

The author has studied the approximate solution of (37) with noisy data according to Tikhonov regularization method with small parameter, which is the solutions of the following variational inequality:

(40)

The solutions of (40) are the elements that satisfy (40). Let’s also denote the solution set of (40) is, with.

The following lemma is necessary for proving the existence of a solution of (5.2).

Lemma 3.1 [12] Suppose T is a operator with defined on the convex subset of X into, hemi-continuous on and f is a below semi-continuous function from X into with f is not identical to infinity. If z is a solution of the variational inequality

then it is also a solution of the variational inequality

Theorem 3.1 If, then.

Proof. We consider the following variational inequality

(41)

We will show that the variational inequality (41) has solutions and that these solutions are also solutions of the variational inequality (37).

From and the property (2) of the operator U it follows that there exists some non-negative real with, as such that

(42)

Since f is a below semi-continuous, convex function, there exist a constant such that

(43)

Indeed, suppose that (43) is not true, therefore there exists some sequence, with and, as, such that

Consequently

or

(44)

From f is a convex function and (44), it follows that

(45)

The inequality (45) is contract with the lower semi-continuous property of f which is mapping any bounded subset of X to bounded set.

Using the monotony of the operator A, we have

(46)

From (41), (43) and (46), it follows that

(47)

From (47), it follows that

(48)

+ If D is not bounded, from the monotone, hemi-continuous of the operator, (48), according to [31] it follows that the variational inequality (41) has the solutions belong to D.

+ If D is bounded, according to [32] , it follows that the variational inequality (41) has the solutions belong to D.

Let z be arbitrary solution of (41), we have

(49)

So, z is a solution of the variational inequality (40), i.e.,.

In case D is an unbounded set, then the following theorem states that the sequence of sets is uniformly bounded.

Theorem 3.2 If and, k is a constant, then the sequence of the sets is uniformly bounded.

Proof. Since, then (Theorem 3.1). Let, then we have

Consequently,

(50)

In inequality (50) we take then

Therefore, in inequality (50) we replace x by, we get

Since, from the above inequality implies

(51)

Since k is not dependent on and since the mapping U turns bounded set into bounded set, the sequence is uniformly bounded. From this, deduce the sequence of sets is also uniformly bounded.

Theorems 3.3 and 3.4 below talk about the stability of the solution of inequality (41) by the Tikhonov regularization method.

Theorem 3.3 With the assumptions given in Theorem 3.2, then the sequence of sets B-weakly converges to the set, as.

Proof. Let, then is uniformly bounded (Theorem 3.2). Since X is a reflexive Banach space, there exists a subsequence of this sequence such that, as. We prove that.

The argument is the same as in the proof of Theorem 3.2, we get the inequality (50) and in this inequality we replace by, we get

(52)

Due to the lower semi-continuity of f and, in (52) given, we get

Since A is hemi-continuous, according to Lemma 3.1, from the above variational inequality, it implies that

So, , that means B-weakly converges to, as.

We enter the following notation

Due to the coercive property of the mapping U on the closed convex set, the set. The following theorem gives a stronger result than Theorem 3.3.

Theorem 3.4 If, then B-converges to, as,.

Proof. Since, , then is small enough, then the sequence of sets is unformly bounded (Theorem 3.2). Let, then is bounded. Since X is a reflexive Banach space, there exists a subsequence of the sequence such that, as,.

The same argument as in the proof of Theorem 3.3, we obtain.

From (52) it follows that

(53)

In (53) given, , we get

According to Minty’s Lemma [30] , from the above variational inequality, we get

So,.

In inequality (53) we replace x by, we get

(54)

We have

(55)

Due to property (3) of the mapping U, from (55) it follows that

This means the sequence B- converges strongly to, as,.

Theorem is proved.

Corollary 3.1 With the same assumptions as in Theorem 3.4, the sequence of sets B-converges strongly to, as,.

Proof. It is easy to deduce from Theorem 3.4 and Proposition 2.1

3.2. Regularization Method Solving the General Variational Inequality with Small Parameter-Weakly Stability

In this subsection, we consider X as a real reflexive Banach space with its conjugate space being strictly convex. Therefore, dual mapping is single, monotone and hemi-continuous [34] .

For the first time, the author studies the approximate solution of the variational inequality (37) by Tikhonov regularization method with small parameter [24] [25] [26] [27] [28] as follows:

Assume that for exact data the exact solution set of (37) is. In fact, instead of knowing this exact data, we only know its approximate data that satisfies the conditions (38) and (39) and, is not necessarily a monotone operator or hemi-continuous.

The author has studied the approximate solution of (37) with noisy data according to Tikhonov regularization method Tikhonov with small parameter, which is the solutions of the following variational inequality:

(56)

The solutions of (56) are the elements that satisfy (56). Let’s also denote the solution set of (56) is, with.

Theorem 3.5. If then the variational inequality (56) has a solution.

Proof. We consider the following variational inequality

(57)

The same argument as in the proof of Theorem 3.1, the variational inequality (57) has a solution in D. Let z be a solution of (57). Due to the monotony of, from (57) it follows that

(58)

We will prove that every solution of (58) is a solution of (57). Indeed, let z be a solution of (58), we have

So,.

Theorem is proved.

In the case that the set D is not bounded, then the following theorem states that the uniformly boundedness of the sequence of sets.

Theorem 3.6 If, , (: constant), then the sequence of the sets of (55) is uniformly bounded in X.

Proof. Since, then (Theorem 3.5). Let, we have

From the variational inequality above, it follows that

(59)

Due to Lemma 2.2, Theorem 3.1, from (59) it follows that

(60)

Due to the monotony of A, from (60) it follows that

(61)

From (58), (59) it follows that

(62)

Due to, from (60) it follows that

(63)

Since, , from (63) it follows that the sequence is uniformly bounded.

Theorem is proved.

The following theorem states B-weakly stability of the solution of the variational inequality (37) according to the Tikhonov regularization method with small parameters.

Theorem 3.7 With the same assumptions as in Theorem 3.6, then the sequence B-weakly converges to, as.

Proof. Since, , , then the sequence is uniformly bounded. Let, then the sequence is bounded in the reflexive Banach space X. Therefore, there exists a subsequence of this sequence such that (since D is the weakly closed set). Since is a solution of (56), we have

Consequently,

Due to Lemma 2.2 and Lemma 3.1, the monotony of A and U, from the above inequality, it follows that

(64)

In (64), taking, we obtain

Due to Lemma 3.1, from the above inequality, it follows that

So,. It means that the sequence B-weakly converges to, as.

Theorem is proved.

We denote, then (since is the convex closed subset in reflexive Banach space X.

The following theorem gives us a stronger result than the above theorem.

Theorem 3.8 If, then the sequence B-strongly converges to, as,. Moreover, if let, , then, as,.

Proof. Since, , then we consider such that

(65)

With satisfying (65), then the sequence is uniformly bounded (Theorem 3.6). Let, then sequence is bounded in the reflexive Banach space X. Therefore, there exists a subsequence of this sequence such that as,. The same argument as in the proof of Theorem 3.7, we get the variational inequality same (64), that is

In this variational inequality, we take, then

Consequently,

(66)

or

Since the sequence is bouned and the function is continuous, then the sequence is bounded. Therefore, in (66) taking, , we obtain

Due to Lemma of Minty, from the above variational inequality, it follows that

Due to the property of dual mapping U, from the above variational inequality, it follows that

So, , that is, the sequence B-weakly converges to, as,.

On the other hand, we have

(67)

From (67) it follows that

In (67) taking, , we obtain

This proves that the sequence has only one limit point, so the sequence itself converges to, as,.

Corollary 3.2 Necessary and sufficient condition for the sequence B-weakly converges to some bounded subset of X as, the variational inequality (40) has a solution.

Proof. Similar to the proof of theorem 2.5.

Remark 3.2: If is monotone operator and, the above results are the same with results in [18] .

We now study the approximate solution of the variational inequality (37) according to Tikhonov regularization method with small parameters, which is the solutions of the following variational inequality:

(68)

where the same assumption of the first of this subset.

The solution of the variational inequality (68) is the elements that satisfy (68). We still denote the solution set of (68) as the set.

Theorem 3.9 If then the variational inequality (68) has a solution.

Proof. The same argument as in the proof of Theorem 3.5, we have the following inequality which has a solution:

(69)

It is easy to show that every solution of (69) is a solution of (68). So,.

Theorem 3.10 If, , (: constant), then the sequence of the sets of (56) is uniformly bounded in X.

Proof. Since, then (Theorem 3.9). Let, we have

Consequently,

Since A is the monotone operator, from the above inequality it follows that

(70)

We have

Consequently,

(71)

Since, from (71) it follows that

(72)

Since, from (72) the sequence is uniformly bounded.

Theorem is proved.

The following theorem talks about B-weakly stability of the solution of the variational inequality (37) by the Tikhonov regularization method with small parameter (68).

Theorem 3.11 With the assumption as in Theorem 3.10. Then, the sequence B-weakly converges to, as.

Proof. From the assumption of Theorem 3.10, then. Let, then the sequence is bounded in the reflexive Banach X, therefore, there exists a subsequence of this sequence such that, as. Since is a solution of (65), we have

Consequently,

(73)

Since the operators are monotone, from (73) it follows that

(74)

Since the function is continuous and lower semi continuous and the sequence is bounded, then in (74) taking, we obtain

So, , that is, the sequence B-weakly converges to, as.

Theorem is proved.

Theorem 3.12 If, , , then the sequence B-weakly converges to. Moreover, let and, then, as,.

Proof. Since, , we consider being small such that

(75)

With satisfying (75), then and is uniformly bounded. Let, then the sequence is bounded in X is a reflexive Banach space, there exists a subsequence of this sequence such that, as,.

The same argument as in the proof of Theorem 3.10, we obtain

(76)

In (76), taking, , due to the continulty of the function and the boundedness of the sequence, we obtain

(77)

Due to Lemma of Minty, from (74) it follows that

Consequently,

So,.

On the other hand,

(78)

In (78) taking, , we obtain

The above argument shows that the sequence has only one limit point, so it is this sequence that converges to, as,.

Theorem is proved.

Corollary 3.2 Necessary and sufficient condition for the sequence B-weakly converges to some bounded subset of X as, the variational inequality (37) has a solution.

Proof. Similar to the proof of Theorem 2.5.

Remark 3.3: We can use Tikhonov regularization methods in Subsections 2.2, 2.3 to find the approximate solution in the given example above.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Lions, J.L. (1972) Some Methods of Solution of Nonlinear Boundary-Value Problems. Mir, Moscow. (Russian Translation)
[2]	Abromov, A. and Gaipova, A.N. (1972) On the Solvability of Certain Equations Containing Monotonic Discontinuous Transformations. USSR Computational Mathematics and Mathematical Physics, 12, 320-324. (In Russian) https://doi.org/10.1016/0041-5553(72)90191-7
[3]	Airpetyan, R.A. and Ramm, A.G. (2000) Dynamical Systems and Discrete Methods for Solving Nonlinear Ill-Posed Problems. Applied Mathematics Reviews, 1, 491-536. https://doi.org/10.1142/9789812792686_0012
[4]	Al’ber, Y.I. (1975) The Solution by the Regularization Method of Operator Equations of the First Kind with Accretive Operators in a Banach Space. Differentsia’nye Uravneniya, 11, 2242-2248. (In Russian)
[5]	Al’ber, Y.I. (1978) Method of Monotonicity and Approximate Computation of the Value of an Unbounded Nonlinear Operator. Siberian Mathematical Journal, 19, 179-183. (In Russian) https://doi.org/10.1007/BF00970498
[6]	Al’ber, Y.I. and Ryazantseva, P. (1979) Solution of Nonlinear Problems Involving Monotonic Discontinuous Mapping. Differensial Uravneniya, 15, 31-42. (In Russian)
[7]	Abramov, A. and Gaipova, A.N. (1972) The Existence of Solutions of Certain Equations That Contain Monotone Discontinuous Transformation. Zh. Vychisl. Mat. i Mat. Fiz, 12, 21-30. (In Russian)
[8]	Browder, F.E (1965) Nonlinear Monotone Operators and Convex Sets in Banach Spaces. Bulletin of the American Mathematical Society, 71, 780-785. https://doi.org/10.1090/S0002-9904-1965-11391-X
[9]	Browder, F.E. and de Figuciredo, D.G. (1966) Monotone Nonlinear Operators in Banach Spaces. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 28, 412-420.
[10]	Browder, F.E. (1966) On the Unification of the Calculus of Variations and the Theory of Monotone Nonlinear Operators in Banach Spaces. Proceedings of the National Academy of Sciences of the United States of America, 56, 419-425. https://doi.org/10.1073/pnas.56.2.419
[11]	Browder, F.E. (1966) Existence and Approximation of Solutions of Nonlinear Variational Inequalities. Proceedings of the National Academy of Sciences of the United States of America, 56, 1080-1086. https://doi.org/10.1073/pnas.56.4.1080
[12]	Browder, F.E. (1967) Nonlinear Accretive Operators in Banach Spaces. Bulletin of the American Mathematical Society, 74, 470-476.
[13]	Browder, F.E. (1968) Nonlinear Maximal Monotone Operators in Banach Spaces. Mathematische Annalen, 175, 89-113. https://doi.org/10.1007/BF01418765
[14]	Browder, F.E. (1969) Nonlinear Variational Inequalities and Maximal Monotone Mappings in Banach Spaces. Mathematische Annalen, 183, 213-231. https://doi.org/10.1007/BF01351381
[15]	Liskovets, O.A. (1983) Regularizaion Problem with Monotone Discontinuous Perturbations of Operators. Doklady Akademii Nauk SSSR, 272, 41-52. (In Russian)
[16]	Liskovets, O.A. (1983) The Regularization Method Solving Problems of Monotone Operators with Non-Monotone Perturbation. Doklady Akademii Nauk, 272, 30-34. (In Russian)
[17]	Liskovets, O.A. (1983) Solution of the First Kind Operator Equations with Non-Monotone Perturbations. Doklady Akademii Nauk SSSR, 272, 101-104. (In Russian)
[18]	Liskovets, O.A. (1983) Solution of the First Kind Operator Equations with Non-Monotone Perturbations. Doklady Akademii Nauk SSSR, 27, 105-109. (In Russian)
[19]	Liu, F. and Nashed, M.Z. (1996) Convergence of Regularized Solutions of Nonlinear Ill-Posed Problems with Monotone Operators. In: Marcellini, P., Talenti, G. and Vesentini, E., Eds., Partial Differential Equations and Applications, Dekker, New York, 353-361.
[20]	Tikhonov, A.N. (1963) Regularization of Ill-Posed Problems. Doklady Akademi Nauk USSR, 151, 49-52. (In Russian)
[21]	Tikhonov, A.N. (1963) Regularization of Ill-Posed Problems. Doklady Akademi Nauk USSR, 153, 501-504. (In Russian)
[22]	Tikhonov, A.N. (1963) Regularization of Ill-Posed Problems. Doklady Akademi Nauk USSR, 156, 25-72. (In Russian)
[23]	Tikhonov, A.N. and Arsenin, V.Y. (1978) Solution of Ill-Posed Problems. John Wiley & Sons, Hoboken.
[24]	Van Kinh, N. (1989) On the Variational Methods to Solve Ill-Posed Problems. Doctoral Thesis, Institute of Matghematics, Hanoi.
[25]	Van Kinh, N. and Chuong, N.M. (1991) Regularization of Variational Inequalities Problems for Non Monotone and Discontinuous Perturbed Operators. Diff. Equations, USSR, 27, 1271-1272. (In Russian)
[26]	Van Kinh, N., Chuong, N.M. and Gorenflo R. (1989) Regularization Method for Solving Approximately Nonlinear Variational Inequalities. Freie Universitat Berlin, Preprint: Nr. A-89-28.
[27]	Van Kinh, N., Chuong, N.M. and Gorenflo R. (1996) Regularization Method for Nonlinear Variational Inequalities. Procceedings of the First National Workshop “Optimization and Control”, Quinhon, 27 May-1 June 1996.
[28]	Van Kinh, N. (2022) Regularization of Ill-Posed Problems with Unbounded Operators. Lambert Academic Publishing, London, 181 p.
[29]	Liskovest, O.A. (1981) The Variational Methods Solving Ill-Posed Problems. Nauka and Tekxika, Moscow, 343 p.
[30]	Vainberg, M.M. (1972) The Variational Method and the Monotonic-Operator Method. Nauka, Moscow. (In Russian)
[31]	Van Chong, L. (1984) On the Existence of Solutions for a General Form of Variational and Quasi-Variational Inequalities. Zeitschrift für Analysis und ihre Anwendungen, 3, 541-548. https://doi.org/10.4171/ZAA/128
[32]	Mosco, U. (1976) Implicit Variational Problems and Quasi-Variational Inequalities. In: Gossez, J.P., Lami Dozo, E.J., Mawhin, J. and Waelbroeck, L., Eds., Nonlinear Operators and the Calculus of Variations. Lecture Notes in Mathematics, Vol. 543, Springer, Berlin, 83-156. https://doi.org/10.1007/BFb0079943
[33]	Bakushinsky, A. and Goncharsky, A. (1994) Ill-Posed Problems: Theory and Applications. Springer, Berlin.
[34]	Hartmann, P. and Stampacchia, G. ((1966) On Some Non-Linear Elliptic Differential-Functional Equations. Acta Mathematica, 115, 271-310. https://doi.org/10.1007/BF02392210