Chebyshev Polynomials with Applications to Two-Dimensional Operators

Alfred Wünsche

Humboldt-Universität, Institut für Physik, Berlin, Germany.

DOI: 10.4236/apm.2019.912050                

Abstract

A new application of Chebyshev polynomials of second kind U_n(x) to functions of two-dimensional operators is derived and discussed. It is related to the Hamilton-Cayley identity for operators or matrices which allows to reduce powers and smooth functions of them to superpositions of the first N-1 powers of the considered operator in N-dimensional case. The method leads in two-dimensional case first to the recurrence relations for Chebyshev polynomials and due to initial conditions to the application of Chebyshev polynomials of second kind U_n(x). Furthermore, a new general class of Generating functions for Chebyshev polynomials of first and second kind U_n(x) comprising the known Generating function as special cases is constructed by means of a derived identity for operator functions f(A) of a general two-dimensional operator A. The basic results are Formulas (9.5) and (9.6) which are then specialized for different examples of functions f(x). The generalization of the theory for three-dimensional operators is started to attack and a partial problem connected with the eigenvalue problem and the Hamilton-Cayley identity is solved in an Appendix. A physical application of Chebyshev polynomials to a problem of relativistic kinematics of a uniformly accelerated system is solved. All operator calculations are made in coordinate-invariant form.

Keywords

Hypergeometric Function, Jacobi Polynomials, Ultraspherical Polynomials, Chebyshev Polynomials, Legendre Polynomials, Hamilton-Cayley Identity, Generating Functions, Fibonacci and Lucas Numbers, Special Lorentz Transformations, Coordinate-Invariant Methods

1. Introduction

The main purpose of this article is to examine an application of the Chebyshev polynomials of both kinds 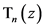and 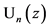to the reduction of two-dimensional operators and its possible generalization to three-dimensional operators with application of the corresponding Hamilton-Cayley identities. This is made in coordinate-invariant form which is shortly sketched in Appendix A.

In the introductory sections we consider the most important properties of these polynomials for our aim. We embed the Chebyshev polynomials into the greater frame of Ultraspherical polynomials which are orthogonal in the finite interval 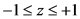and give the connection to the Hypergeometric function 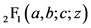with the Jacobi polynomials 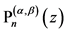as its polynomial case. By this way we consider selected aspects of the Chebyshev polynomials and find also some little known properties and relations, for example, a relation to an integral operator formed from the Bessel functions with the variable substituted by the operator of differentiation which generates a transformed variant of the Ultraspherical polynomials. The methods can be generalized to three-dimensional functions of operators and one partial problem for this is solved in Appendix B.

The Jacobi polynomials and their special case of the Ultraspherical and Gegenbauer polynomials are used in the form in which they were introduced by Szegö [1] (with citations of the “old” original papers) and which became now standard in many monographs about Special functions and Orthogonal polynomials, e.g., [2] [3] [4] , as well as [5] in the NIST Handbook [6] and [7] . A special work about the Chebyshev polynomials is the monograph of Rivlin [8] where the approximation theory of functions takes on a great space.

In present article we investigate the general two-dimensional case of reduction of operator functions via the Hamilton-Cayley identity that seems to be new. This gives also some hints on the three- and higher-dimensional cases which may lead to an approximate conjecture for these forms. In two-dimensional case it leads essentially to an application of Chebyshev polynomials 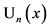and to a general case of Generating functions. The problem connected with the application of the reduction to different operator functions and the calculation of corresponding Generating functions of the polynomials is solved. This is the second great problem for application which we deal with for the two-dimensional case. We attacked but could not finish up to now the solution of some problems which are connected, in particular, with the calculation of Generating functions for the new polynomials in the three-dimensional case. The results may find application in the group theory but many groups with basically three-dimensional operators do not need the general case of three-dimensional operators and the corresponding problems are solved already by more special approaches.

The considerations are important for applications to functions of two-dimensional operators in physics illustrated in Appendix C by an example.

We apply there the Chebyshev polynomials to an interesting problem of relativistic kinematics which uses powers of Special Lorentz transformations for a uniformly accelerated system (space-ship) and which is connected with the application to basically two-dimensional operators. We work with coordinate-invariant methods which are often very advantageous and explain this in Appendix A.

2. Chebyshev and Legendre Polynomials as Special Cases of Hypergeometric Function and Ultraspherical and Gegenbauer Polynomials

We compile in this Section without proof some known basic relations for Chebyshev polynomials of first kind and of second kind 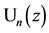including for rationality also Legendre polynomials as intermediate case. This illuminates their position within the Hypergeometric function and their polynomial cases which all are representable as Jacobi polynomials with their special case of Ultraspherical polynomials or, almost fully equivalently to the last, the Gegenbauer polynomials in the standard notations [1] [2] .

The Rodrigues-type formula of the definition of Jacobi polynomials in the very successful form with notation introduced by Szegö [1] is [2] - [8]

(2.1)

The Jacobi polynomials are the following special case of the Hypergeometric function

(2.2)

with the symmetry

(2.3)

A relation connected with an argument transformation in the Jacobi polynomials of the form [1]

(2.4)

together with some modifications using the symmetry of the Jacobi polynomials (2.3) is generally possible. The Jacobi polynomials and all their special cases belong to the classical orthogonal polynomials in a finite interval as which in their standard form is chosen the interval.

Two essentially different expansions of the Jacobi polynomials are

(2.5)

In general, a simple form of the Taylor series of Jacobi polynomials in powers of z does not exist since the summations in formulae for the coefficients

cannot be calculated in closed form. The differentiation of Jacobi polynomials leads again to Jacobi polynomials but with changed parameters

(2.6)

Furthermore, in general, all powers of z from zero up to degree n are included with non-vanishing coefficients in. This changes radically in the special case with powers only in steps of two from the maximal one downwards.

The special case of the Jacobi polynomials is called the Ultraspherical polynomials¹. This case admits the following new representation by the Hypergeometric function in comparison to (2.2)

(2.7)

which is the possible application to (2.2) of a quadratic transformation of Gauss and Kummer [9] (Chapter 2.1.5). There are two almost but not fully equivalent forms of Ultraspherical polynomials and where the lasts are called Gegenbauer polynomials and which are related to each other by

(2.8)

Sometimes, the Gegenbauer polynomials possess advantages in comparison to Ultraspherical polynomials, for example, in case of differentiation

(2.9)

where the coefficients on the right-hand side do not depend on the degree n of the polynomial that, however, is the case for differentiation of (see (2.6)). Despite their equivalence the recurrence relations for the Gegenbauer polynomials possess a simpler form than that for and are

(2.10)

in comparison to

(2.11)

for the Ultraspherical polynomials.

The Ultraspherical polynomials possess a transformation which for even and odd leads to special Jacobi polynomials with transformed argument and unequal upper parameters as follows (Szegö [1] )

(2.12)

They are a consequence of the quadratic transformations of the Hypergeometric function in case of with a result which cannot be expressed by the Gegenbauer polynomials alone.

The Chebyshev polynomials of first kind and of second kind and the Legendre polynomials are important special cases of the Ultraspherical polynomials. In particular, Chebyshev polynomials of second kind are equivalently defined by

(2.13)

and Legendre polynomials by

(2.14)

However, this cannot successfully be continued to upper index since these polynomials are that means they are different from zero only for. Instead of this the Chebyshev polynomials of first kind are

defined by the Ultraspherical polynomials as

(2.15)

They possess unique properties among all Ultraspherical polynomials. The limiting transition used in (2.15) including the number provides

(2.16)

Since is not regularly defined as special case of the Gegenbauer polynomials one has to expect peculiarities in this special case which do not follow from the general case of Gegenbauer polynomials and must be separately derived. For example, they do not satisfy the recurrence relations (2.10) if the polynomials are included. The recurrence relations for the three considered special series of polynomials can be written

(2.17)

This shows that they are the same for both kinds of Chebyshev polynomials. With these recurrence relations the polynomials can be continued to arbitrary negative indices that finds its explanation after transition to trigonometric polynomials (Section 4).

The recurrence relations for and for are specializations

and of (2.10) where that for was additionally divided by the common factors. The recurrence relation for arises from

special case in (2.11) using the definition (2.15) and division by common factors.

3. Series Expansion of Ultraspherical and Gegenbauer, Chebyshev and Legendre Polynomials and Fibonacci and Lucas Numbers

As special cases of Jacobi polynomials the Ultraspherical polynomials and equivalently the Gegenbauer polynomials possess series expansions which follow from (2.5) by corresponding specialization. From the symmetry

(3.1)

follows that the polynomials for even can only contain even powers of z and for odd only odd powers of z. From the two series representations of the Hypergeometric function in (2.5) follow then by reordering of the arising double sums and evaluating the inner sum for the Ultraspherical polynomials

(3.2)

or equivalently for Gegenbauer polynomials

(3.3)

The second representations of the (pure) series in powers of z follows also directly from the representation (2.7) by the Hypergeometric function and its Taylor series expansion.

From the discussed expansions follow in the most important special cases the expansions for:

Chebyshev polynomials of second kind

(3.4)

Legendre polynomials

(3.5)

Chebyshev polynomials of first kind

(3.6)

The first written expansions are the direct specializations from (2.5).

The representations for the Chebyshev polynomials and given at second place in (3.6) and (3.4) lead to the following known interesting representation for, e.g., [5] [7] [8]

(3.7)

and for

(3.8)

According to (2.9) the Gegenbauer polynomials with higher upper parameter can be obtained by differentiation

(3.9)

in particular, from by

(3.10)

The case of Legendre polynomials leads to semi-integer fractional integration (e.g., [10] ) from the Chebyshev polynomials and

corresponding to where are not polynomials but functions which we take from (3.8)²

(3.11)

These integrals can be transformed to a representation by trigonometric functions (see next Section) but, apparently, they are not expressible in short closed form by well-introduced functions.

From the argument substitutions in the Ultraspherical polynomials, in particular, the substitution is interesting. At first, it does not

lead to new polynomials but after multiplication with certain powers of one obtains new polynomials. In [11] we denoted with the following series of (non-orthogonal) polynomials

(3.12)

Inserting this substitution one obtains immediately from (3.2) the following expansions

(3.13)

One may see that the first of the two expansions in (3.13) can be expressed in the following way

(3.14)

Thus the polynomials may be generated by application of an integral operator onto powers of. This integral operator is built by the entire function formed from the Bessel functions according to (see, e.g., [7] [9] )

(3.15)

by the substitution of the variable u by the differentiation operator. It is important that this operator is independent of index n of the generated polynomials³. Making the substitution, in representations of the

Ultraspherical polynomials, for example in (2.7) or in (2.2) with, one may find expressions of the polynomials by the Hypergeometric function. This leads to the following possible expressions (we omit now again the primes)

(3.16)

We consider the simplest special cases.

If we make the substitution of the argument of the Chebyshev polynomials of first kind corresponding to we find

(3.17)

The case to the Legendre polynomials corresponding to cannot be represented in simple way in analogy to (3.7) and (3.8) or (3.17) and we write down the two series expansions obtained by specialization from (3.13)

(3.18)

With the same substitutions of the argument of the Chebyshev polynomials of second kind corresponding to we find

(3.19)

By specialization of the arguments in the derived sequences of polynomials one may obtain sequences of numbers. In certain cases one obtains only integers. To get sequences of positive increasing integers one has to specialize the arguments by complex numbers since the considered polynomials (and also many here not considered polynomials) possess alternating coefficients. In particular, the well-known Fibonacci numbers can be obtained in the following way from the here considered polynomials, series and functions (e.g., [13] for last representation)

(3.20)

The also well-known Lucas numbers can be obtained analogously by ( [13] for last representation)

(3.21)

The Fibonacci numbers possess a known relation to the Golden ratio and to the Chebyshev polynomials of second kind and the Lucas numbers a relation to the Chebyshev polynomials of first kind. They play an important role in combinatorics due to their recurrence relations which are the same for both types and but with different initial numbers

(3.22)

and they are related, among others (multiplicative ones), by [13]

(3.23)

For convenience we give a short table of the Fibonacci and the Lucas numbers (Table 1).

Table 1. Fibonacci and Lucas numbers.

One may construct “similar” kinds of number sequences by changing the arguments of the functions, for example, and

with arbitrary fixed natural numbers N which, obviously,

provide sequences of increasing integers (sometimes under omission of a few initial terms) which in some cases are reducible by divisions. Using other initial values in the same recurrence relations we also get new number sequences (in such cases the sequences are no more described by the here written formulae). We will give yet the following analogous examples of sequences of increasing integers constructed from the Legendre polynomials

(3.25)

A short table of these sequences of numbers is (Table 2).

Table 2. Sequences of numbers.

The importance of such sequences of numbers rises if one finds applications, for example, in combinatorics.

4. Ultraspherical and Gegenbauer Polynomials with Integer and Semi-Integer Parameter

Almost all up to now written relations are true for arbitrary real and even complex variable z. We now consider properties which are only true or possible for real variable x in the basic interval and which are related to Trigonometric functions⁴ and polynomials that leads to a unique property of Chebyshev polynomials of first kind. To these properties belong also the orthogonality relations of the Ultraspherical and Gegenbauer polynomials with their special cases within the basic interval (Figure 1 and Figure 2).

Figure 1. The first 4 Chebyshev polynomials of first and second kind and the first 4 Legendre polynomials and their transforms and.

One may choose another normalization of the Chebyshev and Legendre polynomials according to from which results that leads to more similarity of all Figures. The polynomials and corresponding to and are then directly defined by and the amplitude of the polynomials corresponding to is reduced by the factors and we have (see Figure 2). However, some formulae as, for example, the differentiation of the polynomials become then more difficult than for Gegenbauer polynomials. The same factor could be also excluded in the definition of (3.14).

Figure 2. The first 4 modified Chebyshev polynomials of second kind and their transforms.

These graphics and those for with higher parameter are more similar to the graphics in the first two lines in Figure 1.

If we make the substitution in the Chebyshev polynomial of first kind then we find from the expansions in (3.6)

(4.1)

This is well known and can be easily proved by complete induction. Since one can tentatively define

(4.2)

Clearly the index n, usually the degree of the polynomial within a sequence of polynomials, is here no more true as such. The inversion of relation (4.1) is

(4.3)

or using variable x

(4.4)

that is also easily to prove by complete induction. In the representation of this relation we have already taken into account the continuation of the polynomials to negative indices n.

For the Chebyshev polynomials of second kind one obtains by the substitution in corresponding way from (3.4) the following well-known relations

(4.5)

Using one may continue also in this case the polynomials formally to negative indices n by defining

(4.6)

for all integer n from which immediately follows

(4.7)

The inversion of the relation (4.5) is

(4.8)

or by variable x

(4.9)

Both Formulas (4.4) and (4.9) for the inversion of the Chebyshev polynomials take on their simplest form with the extension of the polynomials to negative indices and, astonishingly, both formula are identical after exchange of the kind of Chebyshev polynomials.

We now calculate which trigonometric functions represent the Gegenbauer polynomials after the substitution. According to (2.9) we find the already complicated expressions

(4.10)

This and the corresponding relations for other integer and semi-integer parameter allows to extend the Gegenbauer polynomials to negative indices with

(4.11)

They are symmetric or antisymmetric with respect to reflection of the index at in dependence on m an odd or an even number. However, the

polynomials make here an exception since they are not determined by the Gegenbauer polynomial which themselves are only determined by a limiting transition.

We now investigate the Gegenbauer polynomials with semi-integer upper parameters. It is hardly possible to find a closed representation for them similar to or to. By

semi-integer integration from we obtain from the already prepared intermediate result by substitution of the integration variable (Gradshteyn, and Ryzhik [7] , 3.675, with hint to Whittaker and Watson [14] )⁵

(4.12)

with the correct special case for,

(4.13)

A closed relation similar to the kind in case of the Chebyshev polynomials is hardly to find for but one may write down expansions. From (3.5), for example, follows

(4.14)

One may transform these results into a series over Chebyshev polynomials of first kind as follows

(4.15)

The more general relation of this kind takes on its simplest form expressed by Gegenbauer polynomials and possesses the form

(4.16)

where it is possible to use the inverse substitution. The basic monomials can be represented by the Legendre polynomials according to

(4.17)

The more general formula expressed in arbitrary Gegenbauer polynomials possesses the form

(4.18)

from which (4.17) is the special case. As hint for attention we mention that a separated factor within the sums in (4.17) and in (4.18) is not a factorial.

In Section 9 we derive a whole class of generating functions for the Chebyshev polynomials. For convenience and to be self-contained we give here the well-known basic generating functions for Chebyshev and Legendre polynomials (e.g., [2] [3] [5] [7] )

(4.19)

and, more, generally for the Gegenbauer polynomials

(4.20)

Another kind of generating functions is (e.g., [5] and [11] )

(4.21)

The more general result is representable by (modified entire) Bessel functions as distinguishing part.

It is sometimes favorable to consider another normalization of the Ultraspherical polynomials or Gegenbauer polynomials as follows⁶

(4.22)

We find then independently of the upper parameters

(4.23)

that is sometimes advantageous and the graphics to different parameter become more similar to each other (see Figure 1 and Figure 2). The recurrence relation becomes

(4.24)

and the formula for the differentiation is

(4.25)

This means, however, that not all formulae become very simple in the form of the polynomials. For example, the formula for the differentiation takes on the most simple form using the Gegenbauer polynomials (see (2.9)) but the last fail to act for the Chebyshev polynomials of first kind. The

special cases of parameters are

(4.26)

It is favorable that the normalization coefficients in are the same as this would be for the favorable choice of the normalization of such as proposed in (3.14). Furthermore, it is favorable that in the extension to negative

indices the sign in the relation in (4.6) changes to a positive sign for according to. More generally, from

(4.11) using relations between factorials of negative and positive numbers then follows

(4.27)

with only positive sign on the right-hand side as advantage. This is true for the general case of with integer and semi-integer parameter.

5. Unique Properties of the Chebyshev Polynomials

We discuss in this Section unique properties of Chebyshev polynomials of first kind and write as variable z when the obtained relations are true for arbitrary complex z. First, we consider composite indices in Chebyshev polynomials of first kind. From (4.1) follows

(5.1)

This means that for composite indices the Chebyshev polynomials possess the nested forms

(5.2)

Thus the Chebyshev polynomial for composite indices n can be found from the Chebyshev polynomials and by the simple nested construction (5.2). This is very similar to the unique decomposition of a natural number into a product of prime numbers and, in principal, the Chebyshev polynomials of first kind need only to be given for prime-number indices and one can build all others in simple way by the nested construction with the possibility of variations by the number of permutations of the prime numbers of the composite index. For example, if we take we can represent the even Chebyshev polynomials in the following two ways

(5.3)

It is easy to construct similar relations, for example, for and to consider many other examples.

We now consider the Chebyshev polynomials of second kind for odd indices. Then from (4.5) follows

(5.4)

or expressed in variable

(5.5)

As example for illustration of this relation we choose and find by specialization of relations in (5.5)

(5.6)

With notation and these polynomials are sometimes separately taken into account in tables. We notice here also a great similarity of relations (5.3) and (5.6) to the relations (2.12) which for

or, respectively, are identical. For arbitrary the relations

(2.12) are a generalization in other direction as the here considered nested relations for the Chebyshev polynomials.

There exist also many interesting relations between Chebyshev polynomials of second and first kind. An interesting relation between Ultraspherical or Gegenbauer polynomials with Chebyshev polynomials of first kind is given in (4.15) and (4.16). All these relations possess a full counterpart in trigonometric identities using (4.1) and (4.5) and this is well known. For example, for the Chebyshev polynomials of second kind with composite indices one may derive in analogous way to (5.5) plus using addition theorems for trigonometric functions the relation

(5.7)

and, in particular

(5.8)

Other forms of identities for are

(5.9)

and for

(5.10)

Many relations for Chebyshev polynomials of both kinds and between them which are connected with recurrence relations and with differentiations one may find in tables (e.g., [2] [3] [5] [7] ).

Another unique property of the Chebyshev polynomials which is restricted to the polynomials of first kind is that for a given function in the interval they provide in approximations of each degree of the polynomial the best approximation by some criteria. One criterium for this is that within the mentioned interval the maximal modulus of the deviation of the approximation from the values of the function is minimal. This was initiated by Chebyshev and further developed by many authors (e.g., Akhieser [15] , Nikolski [16] in [17] , Rivlin [18] ). Via a substitution in the Chebyshev polynomial of first kind this is related to a known similar property of Fourier series in the expansion of periodic functions.

The expansion of functions in series of Chebyshev and, more generally, of Ultraspherical or Gegenbauer polynomials and even Jacobi polynomials is connected with the completeness and orthogonality of these function sets. The completeness for continuous and infinitely continuously differentiable functions in the neighborhood of a considered point is connected with the presence of a polynomial of each degree within the set of polynomials. The known orthogonality relations for the Ultraspherical polynomials within the interval are (e.g., [1] [2] [3] [5] )

(5.11)

In next section we investigate the expansion in Chebyshev polynomials of first kind and consider a mapping onto 2π-periodic functions that leads to Fourier series with an additional symmetry.

6. Relation of Expansions in Chebyshev Polynomials to Fourier Series of 2π-Periodic Functions

We consider the expansion of a sufficiently well-behaved function within the interval in a series of Chebyshev polynomials of first kind

(6.1)

Due to orthogonality relations

(6.2)

the coefficients of the expansion are then determined by the formula

(6.3)

The similarity of expansions of functions within the interval in Chebyshev polynomials of first kind to Fourier series of 2π-periodic functions can be established by an argument transformation in the expansion (6.1), for example⁷

(6.4)

with the new interval corresponding to the primary interval. Then one obtains a 2π-periodic function

(6.5)

however, with a peculiarity. This peculiarity is the additional symmetry

(6.6)

which is already repeated of the same kind after the half of the full 2π-period of the function, in our choice of the transformation (6.4), around according to

(6.7)

and due to 2π periodicity around. In general, due to only 2π-periodicity of the whole function but the symmetries (6.6) and (6.7) are repeated in each further 2π-period (Figure 3).

Figure 3. Example of mapping of function onto function by .

The chosen function is corresponding to.

Using now the relation

(6.8)

then due to symmetry of the expansion (6.1) can be transformed according to

(6.9)

with the coefficients given by integrals not over the full 2π period and with fixed limits

(6.10)

If we use the symmetry (6.6) then the formula for the coefficients (6.10) can be also represented by

(6.11)

with arbitrary. The expansion (6.9) together with (6.11) represents the Fourier decomposition of a general 2π-periodic and symmetric function together with the formula for the coefficients with integration limits which must go only over an arbitrary 2π-interval (Example in Figure 3). Due to additional symmetry (6.6) the formula for the coefficients can be written in the special form (6.10) where the integration limits over a half-period cannot be arbitrarily displaced but only over full 2π-periods.

One may displace the whole picture of to the right by a value on the -axis by choosing a mapping, in particular with

by the mapping. The function is then in last case only symmetric around the values and but not around. One obtains then a Fourier series instead of (6.9) including also sum terms containing with coefficients only specialized in last case by the symmetries around. The mapping to arbitrary period lengths of functions

also does not make difficulties but in all cases we obtain only Fourier series with additional symmetries. Thus the expansion of a function in a series over Chebyshev polynomials to functions is not fully equivalent to a general expansion of an arbitrary periodic function in a Fourier series.

The reason for the additional symmetry in the mapping of functions onto periodic functions from the basic interval onto the basic period of 2π is that the function (and all other similar functions but not Tangent-like functions) is not monotonically increasing but repeats decreasingly its values in the second half of the period 2π. The decomposition of functions into series of the higher Ultraspherical polynomials should provide after the transformation to alternative decompositions of periodic function in comparison to Fourier series with lower importance and, apparently, are not interesting enough up to now.

7. Application of Chebyshev Polynomials of Second Kind to Reduction of Powers of Two-Dimensional Operators

The Chebyshev polynomials of second kind possess an important application in the theory of functions of two-dimensional operators in connection with the Hamilton-Cayley identity. We deal with this in coordinate-invariant form and give the most important informations and basic formulae in Appendix A.

In this section we consider arbitrary two-dimensional operators that means operators which satisfy the following two-dimensional Hamilton-Cayley identity

(7.1)

where and denote the trace and the determinant of the operator according to

(7.2)

which are two independent invariants of the operator with respect to similarity transformations. Our first aim is to reduce powers by means of the Hamilton-Cayley identity (7.1) to linear combinations of the operator and of the identity operator with coefficients which are functions (polynomials) of the invariants of the operator.

First we make a simplification under the supposition of nonvanishing determinant (, non-degenerate case) and introduce a new operator with determinant equal to 1 as follows⁸

(7.3)

Furthermore, we introduced the abbreviations and which play the role of variables in the following considerations. The case of vanishing determinant is either essentially the one-dimensional case or a Jordan normal form with zeros in the main diagonal and one nonvanishing number in the off-diagonal and can be dealt with as a limiting case. We come back to this later. With the introduced variable x the Hamilton-Cayley identity for the operator may be written in the form

(7.4)

From this relation follows for higher powers of

(7.5)

After making some few iterations of the elimination of higher powers of from this equation by means of (7.4) one finds that can be represented in the following form of the superposition of the operators and

(7.6)

where is a polynomials of of the degree n and one sees that the polynomials in front of and of are essentially the same if one first introduces different ones. By complete induction follows with application of (7.4)

(7.7)

that proves (7.6) and we find the necessary recurrence relations for the polynomials

(7.8)

In the special cases follows from (7.6) by comparison with (7.4)

(7.9)

Any two neighbored pairs from these relations can be taken as the initial conditions for the recurrence relations (7.8).

The recurrence relations (7.8) are satisfied by both the Chebyshev polynomials of first kind and by Chebyshev polynomials of second kind (see 2.17) but only the Chebyshev polynomials of second kind obey the initial conditions (7.9) and, therefore, the solution is

(7.10)

Graphical illustrations for the first four polynomials are given in Figure 1.

For an arbitrary function of the operator which can be defined by a Taylor series in a neighborhood of one obtains using (7.10) together with (7.6)

(7.11)

and with separation of the two parts proportional to the identity operator and the operator

(7.12)

For the same function of the more general operator this means

(7.13)

We see from this formula that for the final calculation of this reduction to a linear combination of the operators and for a given function one should possess the result for the corresponding sums in (7.13) containing the Chebyshev polynomials of second kind. They may be considered as Generating functions to these polynomials in a wide sense.

8. Solution of Eigenvalue Problem for Two-Dimensional Operators and Arbitrary Functions of Operators

In this section, we calculate functions of two-dimensional operators and represent these as superposition of the two linear independent operators and. As preparation we consider the solution of the eigenvalue problem of the operator in coordinate-invariant form.

The solution of the eigenvalue problem of two-dimensional operators

(8.1)

consists of the determination of the eigenvalues by means of the secular equation

(8.2)

and the determination of right-hand eigenvectors and left-hand eigenvectors to the eigenvalues. Instead of the eigenvectors, we determine below projection operators to these eigenvectors. We denote the two, in general, different solutions of the eigenvalue Equation (8.2) by according to

(8.3)

where the substitutions (7.3) are used. It does not make a restriction of the generality to suppose nondegeneracy of the eigenvalues because the degenerate case can be dealt with by a limiting procedure that, however, is not necessary to this moment for our purpose.

Using the Hamilton-Cayley identity (7.1) we now define the complementary operator to an arbitrary two-dimensional operator by

(8.4)

First of all, the complementary operator serves for the determination of the inverse operator to according to

(8.5)

Then one may determine projection operators and to the eigenvalues and by

(8.6)

It is easy to see that are projection operators for the determination of eigenvectors to the eigenvalues and that they satisfy the relations

(8.7)

for arbitrary vectors and. This means that is either a right-hand eigenvector of to eigenvalue or is vanishing and is either proportional to or is vanishing, correspondingly. The identity operator, the operator and arbitrary operator functions can now be represented by means of the projection operators and in the following way

(8.8)

By inserting in (8.6) the explicit form of the eigenvalues given in (8.3), we find the following representation of

(8.9)

where again the substitutions (7.3) are used. In the same way, we find

(8.10)

According to (8.8), an arbitrary operator function can be represented in the following way by a linear combination of the operators and

(8.11)

where and are defined in (7.3) as parameters from the invariants of the operator. This has the same form as the representation in (7.13) and the identification of the functions in front of and provides Generating functions for the Chebyshev polynomials of second kind. We discuss this in the next section.

As first example for the reduction of a function of the operator to a superposition of the operators and we find from (8.11)

(8.12)

The case of with arbitrary is similar but with few possibilities for simplifications in comparison to the general Formulae (8.11).

Another interesting example is the function for which we find from (8.11)

(8.13)

where we used the identity

(8.14)

The important case of an exponential function is separately discussed in Section 10.

9. A Whole Class of Generating Functions for the Chebyshev Polynomials of Both Kinds

With (7.13) and (8.11) we derived in Sections 7 and 8 two different representations of functions of an arbitrary two-dimensional operator expressed by the two independent basic operators and. These two representations have to be equal. If we separate the parts proportional to the identity operator and to the operator we obtain first from terms proportional to the identity

(9.1)

and second from terms proportional to the identity

(9.2)

Both identities possess the form of generating functions for the Chebyshev polynomials of second kind. They have a very general form for arbitrary functions for which the derivatives at are well defined and thus the function can be expanded in a Taylor series around this point. By a certain linear combination of these identities of a kind which can be seen from the separated initial terms one obtains the identity

(9.3)

where we used the relation (provable by complete induction or by trigonometric equivalent)

(9.4)

Using and the identity (9.3) can be written

(9.5)

and the identity (9.2) using

(9.6)

Apart from the monomials in the Taylor series of itself we do not know other complete sets of polynomials for which Generating functions are derived up to now in such generality.

We may check for the functions that the Formulas (9.5) and (9.6) lead directly to (known) representations of the Chebyshev polynomials of second and first kind (see (3.7) and (3.8)). As a first other function we consider

(9.7)

Then from (9.5) and (9.6) easily follows

(9.8)

The relation which follows from (9.1) is a linear combination of these identities.

Next we consider an exponential function

(9.9)

Then from (9.5) and (9.6) follows (compare with (4.21))

(9.10)

These generating function are also known and are affirmed by program “Mathematica”.

We consider a third example with analytic modified Bessel functions at and with the parameter (compare with similar function (3.15))

(9.11)

For this function follows from (9.5) and (9.6)

(9.12)

Another interesting example is related to the function

(9.13)

For this example one finds

(9.14)

By separation of the even and odd parts with respect to variable t one may gain further Generating functions.

10. Exponential Function of a General Two-Dimensional Operator

In this section we consider in detail the exponential function of a two-dimensional operator. It is important for applications, for example, in group theory. From general case (8.11) we specialize

(10.1)

The operator is here decomposed into a product of two commuting operators. The first operator

(10.2)

is proportional to the identity operator and its determinant is the exponential of the trace of the operator. The last is a general property for the determinant of an exponential function of an arbitrary operator and follows almost immediately from the eigenvalue decomposition of the operator. The second operator in braces

(10.3)

is the exponential of an operator here abbreviated with vanishing trace. Its determinant is therefore equal to 1. If we denote in analogy to (7.3) the parameters of the operator by and where is vanishing due to vanishing trace then we find for the reduction of the exponential of the operator

(10.4)

This is identical to the more specialized representation of the operator with vanishing trace of the operator in the exponent in braces in (10.1).

A vanishing trace of an operator is usually obtained from the assumption of its antisymmetry according to

(10.5)

where the superscript '' means the transposition. The problem is that in a general linear or in an affine space this cannot be defined and that it requires an Euclidean or Pseudo-Euclidean space with definition of a symmetrical scalar product and thus of a symmetrical metric tensor⁹.

We mention that a two-dimensional operator can be reduced to a superposition of the operators and using the Hamilton-Cayley identity for in the exponent according to

(10.6)

where can be dealt with as the operator by corresponding substitution.

11. Degenerate Cases

The two-dimensional case of operators does not admit many degenerate cases.

We now make some short remarks about the case of degeneracy of the eigenvalues that means about the coincidence. A necessary and sufficient condition is the vanishing of the root in (8.3) that is the condition

(11.1)

Substituting in the Hamilton-Cayley identity (1), we find

(11.2)

This shows that is a quadratic nilpotent operator in case of degeneracy of the eigenvalues. We have to distinguish two subcases of different volume and.

In case of, the projection operators in (9) are no more defined. It can immediately be seen from (11.2) that for arbitrary vectors is either a right-hand eigenvector of or is vanishing and analogously for with regard to left-hand eigenvectors of. Due to , the left-hand and right-hand eigenvectors are orthogonal to each other. This is the case where the matrix to the whole operator forms a two-dimensional cell in the Jordan normal form and where it cannot be diagonalized by means of a similarity transformation.

In case of, the operator is proportional to the identity operator with the eigenvalue as proportionality factor.

We consider now the special case if the determinant of the operator is vanishing. Then the operator has a vanishing eigenvalue and due to Hamilton-Cayley identity we have

(11.3)

This means that the operator is idempotent in this case with trace equal to 1 if

(11.4)

The second eigenvalue is equal to and the operator is projection

operator for the determination of right-hand and left-hand eigenvectors to the eigenvalue according to

(11.5)

that results from the Hamilton-Cayley identity (7.1) under the supposition. For this case follows from (11.3)

(11.6)

If in addition to also the trace is vanishing then due to the Hamilton-Cayley identity (7.1) is vanishing (nilpotent)

(11.7)

and either itself is vanishing and

(11.8)

or it is non-vanishing and from (11.6) follows

(11.9)

The operator belongs in case of then to a Jordan normal form with only one non-vanishing element in one of the off-diagonals and is quadratically nilpotent.

12. Conclusions

A main result of this article was to show that the Chebyshev polynomials in connection with the two-dimensional Hamilton-Cayley identity can solve the problem of reduction of functions of two-dimensional operators to superpositions of this operator itself and of the identity operator in coordinate-invariant form. In Appendix C this is applied to an interesting problem of relativistic kinematics of a step-wise accelerated space-ship with final transition to a uniformly accelerated space-ship seen from the inertial systems of earth and of the space-ship. The solution of this problem uses in an intermediate step Chebyshev polynomials of first and of second kind. An aim was to generalize the application to functions of three-dimensional operators which need a generalization of the Chebyshev polynomials to polynomials which essentially depend on two continuous variables. The derived recurrence relations are 4-term relations instead of 3-term relation for the usual Chebyshev polynomials. The solution of this programme seems to be interesting for three-dimensional operators, in particular, in group theory. This programme is a difficult one and is not yet accomplished with present article. However, we could explicitly obtain the (here not presented) necessary polynomials but some properties and interesting relations, in particular, the desirable Generating functions for these polynomials are not obtained up to now.

In the introductory sections we discussed some properties of the Chebyshev polynomials, and tried to consider them within the more general sets of the Ultraspherical and of the widely equivalent Gegenbauer polynomials and included also the Legendre polynomials which take on an intermediate place between the Chebyshev polynomials of first and of second kind. We compiled mainly the formulae which are connected with explicit representation in form of expansions in power series and discussed trigonometric forms. Clearly, much is known but we obtained also here some new shades. For example, after a variable transformation within the Ultraspherical polynomials we obtained in Section 3 a set of polynomials which could be generated from the basic monomials by an operator which essentially uses the Bessel functions with the variable substituted by the operator of differentiation, and which does not depend on the degree of the polynomial and which was earlier applied in analogous form with success to Hermite polynomials. We mentioned the connection of Chebyshev polynomials to Fibonacci and Lucas members and showed possibilities to obtain other increasing sequences of integers from Ultraspherical polynomials. In many ways the Chebyshev polynomials of fist kind take on a peculiar position which does not fit to the general classes of Ultraspherical or Gegenbauer polynomials. At the end of Section 4 it is shown that this can be removed by another normalization of the Ultraspherical polynomials with some attractive properties but also with some less attractive properties. The exceptional position of the Chebyshev polynomials of first kind within the family of Ultraspherical polynomials is underlined by the short discussion of two properties. Similar to the role of prime numbers for all (composite) numbers the Chebyshev polynomials of first kind need only those with prime degree as building stones which allow the construction of all other Chebyshev polynomials of first kind by nested inclusions. The second exceptional property of Chebyshev polynomials of first kind is that in power series expansions within a given finite interval (which can be managed by transformations) in each degree they provide the best approximation by some criteria compared with the other sequences of Ultraspherical polynomials. This is in analogy to Fourier series in comparison to expansions of periodic functions in other complete sets of basic periodic functions. In Section 6 we mentioned shortly the mapping of the expansion in Chebyshev polynomials of first kind onto Fourier series and show that the obtained Fourier series possess an additional symmetry in comparison to general Fourier series.

Appendix A: Hamilton-Cayley Identity in General N-Dimensional Case

Let be a linear operator in an N-dimensional linear space. This operator satisfies the Hamilton-Cayley identity (e.g., [19] [20] [21] )

(A.1)

with identity operator and with the coefficients which appear also as coefficients in the following eigenvalue equation of the operator to eigenvalues

(A.2)

The determinant of an arbitrary N-dimensional operator is here denoted by and later its trace by for arbitrary dimension.

The eigenvalues and the related coefficients are invariants of the operator with respect to similarity transformations by arbitrary nonsingular operators

(A.3)

The relation between the coefficients and the eigenvalues up to their order is reversibly unique and is simple for the traces and for the determinants and is more complicated for the other invariants.

The determinant arises primarily as the coefficient of the transformation of the completely antisymmetric volume product

(A.4)

where s is an arbitrary permutation of N elements and the sign of the permutation (perm.), when transforming the N linearly independent vectors into N other vectors by the linear operator operator according to

(A.5)

If is a set of N basis vectors then an arbitrary vector and may be represented by (sum convention)

(A.6)

Using now the fully antisymmetric unit pseudo-tensor (or Levi-Civita symbol) for the representation of the volume product V by the vector components in the basis we find

(A.7)

where is the volume product of the basis vectors (volume of elementary cell) and the Levi-Civita symbol is defined by

(A.8)

with s an arbitrary permutation according to (A.4). For the determinant according to definition (A.5) one finds then

(A.9)

where is defined in fully equal way to in (A.8) only written with upper indices. The determinant tensor can be represented by the Kronecker symbol according to

(A.10)

Clearly, all this is well known in one or the other form and serves here for the introduction of some of our notations.

To our experience, in coordinate-invariant calculations up to four-dimensional cases (in particular, three-dimensional case in optics of anisotropic media) it is very favorable to possess a notation which distinguishes the invariants from vectors and operators and is easily to recognize as such. We introduced the notation for the trace of an operator in arbitrary dimension and denote the other invariants with respect to similarity transformations as follows

(A.11)

These notations are compatible concerning the dimension. For three-dimensional operators we have and is the determinant and for two-dimensional operators we have and together and is the determinant but all other relations remain the same. The Hamilton-Cayley identity in four-, three- and two-dimensional case are ()

(A.12)

Formally, the descent by one dimension is the division of the Hamilton-Cayley identity by the operator. The inverse operator to a given operator can easily be calculated in coordinate-invariant way using the Hamilton-Cayley identity of the corresponding dimension.

The great initiator of coordinate-invariant methods in optics of anisotropic media, in the theory of the Lorentz group and in elasticity theory was F.I. Fyodorov from Minsk [21] (he called this Covariant methods) and also we published in the seventies some papers to the optics of anisotropic media with application of coordinate-invariant methods (approximately 10 in “Ann. d. Physik”) which we do not cite here. However, we hope that we find opportunity to represent much more about the very favorable coordinate-invariant methods in future.

Appendix B: Eigenvalue and Eigenvector Problem in Three-Dimensional Case in Coordinate-Invariant Form

We consider here the case of three-dimensional operators and sketch the solution of the problem to determine eigenvectors to eigenvalues in coordinate-invariant form.

An operator is three-dimensional if it satisfies the three-dimensional Hamilton-Cayley identity

(B.1)

The meaning of the invariants is given in (A.11) where and all higher invariants are also vanishing in three-dimensional case. Due to the Hamilton-Cayley identity (B.1) all powers and functions can be reduced to superpositions of the operators and.

The complementary operator to the operator is defined in three-dimensional case as follows

(B.2)

The inverse operator can be expressed by the complementary operator as follows

(B.3)

For the complementary operator using the three-dimensional Hamilton-Caylex identity (B.1) for the reduction of follows generally

(B.4)

We consider first the special case of an eigenvalue of and then the general case. For eigenvalue it is necessary that the determinant of is vanishing that means and according to (B.4) we have then

(B.5)

An arbitrary vector is right-hand eigenvector and an arbitrary vector is left-hand eigenvector of to eigenvalue if

(B.6)

Therefore, the operator is projection operator to the determination of right-hand and left-hand eigenvectors of the operator to eigenvalue. We consider here only the non-degenerate cases and and do not normalize the eigenvectors. All this can be managed.

We consider now an arbitrary eigenvalue of a three-dimensional operator that means

(B.7)

It has to satisfy the eigenvalue equation

(B.8)

For the complementary operator to the operator we find

(B.9)

and its trace is

(B.10)

Therefore, the projection operator for the determination of eigenvectors to the (non-degenerate) eigenvalue of the operator is

(B.11)

With the three, in general, different eigenvalues (non-degenerate case) of a three-dimensional operator one may represent functions of this operator in the following form

(B.12)

In this way, the functions of the operator are reduced to superpositions of the three operators with coefficients which are functions of the invariants. Mainly for lack of place we do not consider here degenerate cases. Clearly, it is difficult to write all this explicitly together with the solutions of the eigenvalue Equation (B.8) by the Cardano formulae. On the other side, one may make the reduction of powers also by introduction of two new sets of polynomials of two variables leading to new identities similar to the case of two-dimensional operators which leads to Chebyshev polynomials of second kind and to a general kind of Generating functions as demonstrated.

Appendix C: An Application of Chebyshev Polynomials to Powers of Special Lorentz Transformations

Notation: Vectors bold types, scalar product, vector product, dyadic product of two vectors and with trace.

We deal with here an interesting example where the application of Chebyshev polynomials of first and of second kind plays a role. It is connected with powers of Special Lorentz transformation which are, essentially, two-dimensional operators although we calculate with four-dimensional operators and the results are interesting for a uniformly accelerated space-ship.

We consider two inertial systems I and I'. In the inertial system I which we consider as resting (say earth) a body (say space-ship) starts with a velocity and remains with this velocity in the inertial system meaning that it rests there and after a certain time starts from this inertial system again with the same velocity to a new inertial system and moves there with a new velocity considered in the primary system I. We repeat this in n steps and ask for the velocity with which the space-ship moves in relatively to I. It does not play a role that in each new inertial system the velocity is enlarged by a finite velocity in comparison to the preceding inertial system that is not really makable since at the end we make a limiting transition to a constant acceleration by smaller steps in smaller times and go to the limit of infinitely small steps. This is a problem of kinematics of Special Relativity theory where one has to calculate the product of n Special Lorentz transformations and may consider then the limiting case.

It is well known that the Special Lorentz transformation from of a space vector and a time t from inertial system I to inertial system I' moving with velocity in I possesses the form

(C.1)

with the abbreviations (c is light velocity)

(C.2)

The inversion of (C.1) to in dependence on can be made by the substitution in (C.1). In separation of the space vector in parts parallel and perpendicular to the Lorentz transformation (C.1) takes on the form

(C.3)

The Special Lorentz transformations of wave vectors and frequencies is

(C.4)

or by separation of the wave vector in analogy to (C.3)

(C.5)

In four-dimensional wave-vector-frequencies k and space-time vectors r according to

(C.6)

one has to require the invariance

(C.7)

The Special Lorentz transformation can be represented then in four-dimensional coordinate-invariant form as, e.g. [22] (§16)¹⁰

(C.8)

It is now evident that according to

(C.9)

the required invariance (C.7) is satisfied.

The transformation from inertial system I after n described steps to is made by the n-th power of. It is clear that it must possess the same structure as (C.8) that means

(C.10)

and due to the same direction of the velocity in each step we have

(C.11)

The general result is

(C.12)

Therefore the n-th power (C.10) of the Lorentz transformation can be written explicitly

(C.13)

With one easily finds that leads to given in (C.8) and also the case using and leads to the identity operator I according to

(C.14)

as the correct result.

With the two identities (see also (3.7) and (3.8))

(C.15)

and using it in (C.12) with the substitution (see (C.2)) one finds for the velocity expressed by in relation to the light velocity c

(C.16)

where we used (see (C.2)) and introduced coefficients and obtain

(C.17)

The coefficients are factors which characterize how near the modulus of the velocity after n described steps in inertial system comes in comparison to the primary inertial system I of the earth.

We now make the limiting transition from discrete steps of addition of a velocity in every step in inertial systems to a continuous function under the assumption that this increase happens to constant time intervals and introduce a constant acceleration by definition

(C.18)

In the system connected with the space-ship the last is to every time in its coordinate origin if it was at time in the coordinate origin of the inertial system I that means at to the time. We now consider a time in the systems of the space-ship and make with

in Formula (C.17) the following limiting transition

(C.19)

where we used the well-known limiting transition. With

the meaning of one obtains then the velocity of the space-ship in the inertial system I expressed by the time in the space-ship or what is the same the negatively taken velocity of the earth in the proper time of the space-ship with simple result

(C.20)

The limiting transition for provides

(C.21)

in proper time in the system of the spaceship.

The transformation of the time T' from system of the space-ship to corresponding T of the system I of earth can be made by using the inversion of (C.1) to in dependence on and setting in the space ship (time dilatation) and due to dependence of on time we have to start from the differential form of this relation

(C.22)

The integration of both sides provides

(C.23)

with the inversion

(C.24)

This is the transition of the time T' from the space-ship to the corresponding time T in the system of earth and means that the time up to arrival to an object is for the space-ship travelers smaller than for the earth residents.

The way which the space-ship travels in the inertial system I expressed by the time of the space-ship or negatively taken the way of the earth seen from the space-ship in its proper time can be found by integration of

(C.25)

The integration from up to a time T' provides

(C.26)

To find the way which takes the space-ship to the proper time T in the system I of earth one has to substitute T' according to (C.24) by T but this is not directly controllable since we cannot have an instant connection with the system of the space-ship and the times in each of the two systems are synchronized before. With the Formulae (C.4) one may discuss the change of wave vectors and frequency of signals sent from the system of space-ship to earth or inversely that we will not do here.

We do not discuss the formulae here more in detail and mention that the transition to a continuous acceleration (no more an inertial system) is also not without problems¹¹.

NOTES

¹The name results from the Spherical harmonics which can be represented by the following formula , where depends only on as continuous variable. Among others the polynomials possess the following representation by Ultraspherical polynomials (positive sign of is to choose) and are called Associated Legendre polynomials (Legendre polynomials in case).

²The lower limit of the standard fractional integral is here substituted by. With lower limit the integral would become undetermined at and would not provide correct values for. The correct integrals after transformation to trigonometric functions correspond to the chosen lower limit (next Section).

³In analogous way the Hermite polynomials can be generated by application of the integral operator onto the basic monomials according to that played an important role in our previous papers to this subject, e.g. [12] . This suggests to use also other entire functions and to substitute their variable by the differentiation operator and then to apply this to the sequence of basic monomials but this makes only sense if one may find applications or interesting aspects of the obtained sequence of (usually, non-orthogonal) polynomials.

⁴Outside this basic interval they are related to corresponding Hyperbolic functions.

⁵The presence of this integral in tables admits the conjecture that someone already went the way via fractional integration but there in [14] (§15.321) we find (now old) citations of Dirichlet and of Mehler. However, they provide no other closed result or representation than the Legendre polynomials whereas we started from it, possibly in the hope, to find other representations similar to (4.1) and (4.5).

⁶We made a bracket around the upper parameter to distinguish them from the different Associated Legendre polynomials where the upper indices m can take on only integer values (see also footnote in Section 2).

⁷We choose the Minus in front of since we want that the interval is mapped onto the part of the whole interval by a monotonically increasing function.

⁸Properly speaking, we get two related operators as possible results of the substitution depending on the choice of the sign of that does not possess influence on the following considerations.

⁹By means of a symmetrical metric tensor one may define using covariant and contravariant indices a tensor from which follows having used the symmetry of and now the antisymmetry of means.

¹⁰The transformation of space and time for the part parallel to the velocity is essentially a two-dimensional one.

¹¹In addition, we are also not sure what is already calculated and discussed in the literature of astrophysics and space travels and bring this as an application of Chebyshev polynomials.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Szegö, G. (1959) Orthogonal Polynomials. 2nd Edition, American Mathematical Society, New York.
[2]	Erdélyi, A. (1953) Higher Transcendental Functions, Volume II. McGraw-Hill, New York.
[3]	Abramowitz, M. and Stegun, I. (1965) Handbook of Mathematical Functions. Dover Publication, New York.
[4]	Nikiforov, A.F. and Uvarov, V.B. (1974) Osnovy teorii spetsialnykh funkzij (Fundaments of the Theory of Special Functions). Nauka, Moskva.
[5]	Koornwinder, T.H., Wong, R., Koekoek, R. and Swarttouw, R.F. (2019) Orthogonal Polynomials. In: NIST Handbook, Chapter 18, NIST, Gaithersburg, MD, 435-484.
[6]	Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark C.W. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
[7]	Gradshteyn, I.S. and Ryzhik, I.M. (1963) Tables of Series, Products and Integrals. 4th Edition, Nauka, Moscow (Translation into Other Languages and Later Editions Exist).
[8]	Rivlin, T. (1990) Chebyshev Polynomials, From Approximation Theory to Algebra and Number Theory. 2nd Edition, John Wiley and Sons, New York.
[9]	Erdélyi, A. (1953) Higher Transcendental Functions, Volume I. McGraw-Hill, New York.
[10]	Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus. Academic Press, New York.
[11]	Wünsche, A. (2015) Operator Methods and Symmetry in the Theory of Jacobi and of Ultraspherical Polynomials. Applied Mathematics, 7, 213-261. https://doi.org/10.4236/apm.2017.72012
[12]	Wünsche, A. (2015) Generating Functions for Products of Laguerre 2D and Hermite 2D Polynomials. Applied Mathematics, 6, 2142-2168. https://doi.org/10.4236/am.2015.612188
[13]	Conway, J.H. and Guy, R.K. (1996) The Book of Numbers. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4612-4072-3
[14]	Whittaker, E.T. and Watson, G.N. (1927) A Course of Modern Analysis. 4th Edition, Clarendon Press, Cambridge.
[15]	Akhieser, N.I. (1963) Theory of Approximation. MacMillan Company, New York.
[16]	Nikol’ski, S.M. (1969) Approximation of Functions. Chapter 12. M.I.T. Cambridge (Mass.), 265-302.
[17]	Aleksandrov, A.D., Kolmogorov, A.N. and Lavrent’ev, M.A. (1999) Mathematics Its Content, Methods and Meaning. Dover Publications, Mineola, NY.
[18]	Rivlin, T. (1981) An Introduction to the Approximation of Functions. Dover Publication, New York.
[19]	Gantmakher, F.R. (1954) Teoriya Matrits. Gostekhisdat, Moskva. [In German: Gantmacher, F.R. (1958) Matrizenrechnung, Dtsch. Verl. d. Wissenschaften, Berlin. In English: Gantmacher, F.R. (1960) The Theory of Matrices. Chelsea Publishing, New York.]
[20]	Mirski, L. (1955) An Introduction to Linear Algebra. Clarendon Press, Oxford.
[21]	Fyodorov, F.I. (1958) Optika anisotropnykh sred (Optics of Anisotropic Media), (Optic of Ansiotropic Media). Isdatel’stvo AN BSSR, Minsk.
[22]	Fock, V.A. (1966) The Theory of Space, Time and Gravitation. 2nd Edition, Pergamon Press, Oxford [Russian Original: Fizmatgiz, Moskva (1961).]