Optimal Bounds for the Largest Eigenvalue of a 3 × 3 Correlation Matrix

Werner Hürlimann^*

Swiss Mathematical Society, Fribourg, Switzerland.

DOI: 10.4236/apm.2015.57039                

Abstract

A new approach that bounds the largest eigenvalue of 3 × 3 correlation matrices is presented. Optimal bounds by given determinant and trace of the squared correlation matrix are derived and shown to be more stringent than the optimal bounds by Wolkowicz and Styan in specific cases.

Keywords

Correlation Matrix, Positive Semi-Definite Matrix, Extreme Point, Eigenvalue, Inequality

1. Introduction

The topic of bounds on eigenvalues of symmetric matrices has a long history (e.g. [1] , Chap. III). In some situations optimal bounds have been found. For the set of complex matrices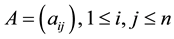, with real eigenvalues, Wolkowicz and Styan [2] obtained optimal bounds by given 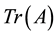and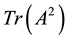. For the same set of matrices with positive eigenvalues, Merikoski and Virtanen [3] [4] have studied optimal bounds by given and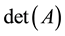. Zhan [5] obtained the optimal bounds for the smallest and largest eigenvalues of real symmetric matrices whose entries belong to a fixed finite interval. However, when restricted to the set of real 3 × 3 correlation matrices, these bounds collapse to useless or trivial bounds, as argued in the Remarks 2.1. Moreover, for correlation matrices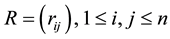, with unit diagonal elements, one has always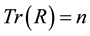. Therefore, the separate knowledge of 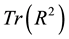and does not exhaust the complete information about a correlation matrix, even in the case of 3 × 3 correlation matrices. It is therefore justified to search for further possibly optimal bounds on eigenvalues for correlation matrices.

The present study is devoted to a new approach for bounding the largest eigenvalue of 3 × 3 correlation matrices. In Theorem 2.1 we derive some new optimal bounds by given determinant and trace of the squared correlation matrix. They are compared in Theorem 3.1 to the optimal bounds in [2] and found to be more stringent in some specific cases. Section 4 illustrates with some numerical comparisons.

2. Bounds by Given Determinant and Trace of the Squared Correlation Matrix

Starting point is a real 3 × 3 matrix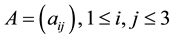, with characteristic polynomial

(2.1)

where 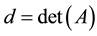is the determinant, and 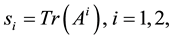are the traces of the matrix and its square. Each zero of this polynomial is called an eigenvalue (EV). Expressed in terms of the variable 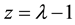one finds the polynomial

.

Restricting the attention to correlation matrices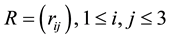, with unit diagonal elements, one has and the polynomial simplifies to the “depressed cubic”

(2.2)

The set of correlation matrices is uniquely determined by the set of 3 upper diagonal elements , denoted by. For convenience, we use throughout the algebraic notation . It is known that, up to permutations, an element if, and only if, one has, , where the interval bounds characterize the extreme points of the elliptope (e.g. [6] , Theorem 3.1, and [7] , Theorem 3.1). Since and, the coefficients of the cubic in (2.2) are given by

(2.3)

We ask for possibly optimal bounds for the largest EV (LEV) of a correlation matrix by given and, or equivalently by given, which is the maximum available information. The following sharp inequality, which characterizes the semi-definite property of a 3 × 3 correlation matrix, is trivial but an essential ingredient of the analysis.

Lemma 2.1. For all one has the inequality. It is attained at the extreme points of consisting of all.

In the following, we assume first that, that is the EVs are not all one, that is, and in particular. Therefore, one searches for the positive zero of the depressed cubic (2.2). Making use of the identity rewrite the latter in two different ways:

(2.4)

Using that, one sees that a positive zero of these two cubic polynomials necessarily satisfy the two quadratic inequalities

(2.5)

In terms of the possible ranges of validity of these inequalities are as follows:

Inequality (I)

(2.6)

By Lemma 2.2 below the square root is always real. The lower bound is non-negative provided, a restriction assumed in this case.

Inequality (II)

(2.7)

The square root is real provided, which is assumed in this case. If the inequality (II) is always satisfied and no information, besides, about the LEV is gained herewith. The upper bound

is non-negative provided, a restriction assumed in this situation.

Lemma 2.2. For all one has the inequality.

Proof. Clearly, one has if, and only if, one has.

Case 1:

One has and the inequality is fulfilled.

Case 2:

One has. Set. Then, for fixed one must have. If then the inequality is always fulfilled. If then rewrite. Since this is minimum for, and. Since the function is minimum at, one gets.

How are the feasible inequalities (I) and (II) linked? Lemma 2.1 implies the inequalities

(2.8)

where the first and third inequalities are attained at the extreme points, and the middle one is attained when. These inequalities restrict the number of LEV bounds to the meaningful combinations stated in the main result below. For convenience, we parameterize elements as univariate functions. Similarly, the coefficients in (2.3) are parameterized as ,. The result depends upon defined if.

Theorem 2.1. (Optimal bounds for the LEV of a 3 × 3 correlation matrix). The largest eigenvalue of a 3 × 3 correlation matrix satisfies the following bounds:

Upper bound

Case (A):

The upper bound is attained at the extreme points.

Lower bound

Case (B):

Sub-Case (B1):

Sub-Case (B2):

The lower bound is attained at the extreme points.

Case (C1):

Sub-Case (C11):

Sub-Case (C12):

The lower bound is attained at the “zero” correlation matrix.

Case (C2):

Sub-Case (C21):

Sub-Case (C22):

The lower bound is not attained, but in the limit as one has.

Remarks 2.1. If the bounds are attained, that is in the cases (A), (B) and (C1), they are the best bounds by given, or equivalently,. It is interesting to compare the new optimal bounds with related results, which deal, however, all with larger sets of matrices. For complex matrices

, of arbitrary dimensions with real eigenvalues, Wolkowicz and Styan [2] obtained optimal bounds by given and, called hereafter WS bounds. Albeit this is not the available maximum

information for 3 × 3 correlation matrices, a detailed comparison with the WS bounds is instructive and provided in Section 3. In contrast to this, for the same set of matrices with positive eigenvalues, the bounds in [3] by given and, hereafter called MV bounds, are not optimal, that is not attained for a specific matrix with the given properties. Even more, the best possible bounds cannot in general be expressed algebraically, as shown in [4] . More recently, Zhan [5] obtains the optimal bounds for the smallest and largest eigenvalues of real symmetric matrices whose entries belong to a fixed finite interval. However, when restricted to the set of real 3 × 3 correlation matrices, the Zhan bounds collapse to useless or trivial bounds ([5] , Corollary 2 (ii), p. 854, Theorem 5 (ii), pp. 854-855). Information on further possible comparison statements are provided in Section 3.

Proof of Theorem 2.1. It is clear by (2.6) and (2.8) that the upper bound in Case (A) must hold. Equality in (I) is attained when, that is by Lemma 2.1. To derive the lower bounds suppose first that. Then, the lower bound in (2.7) is defined and by (2.8) it must imply a lower bound for the LEV. Again, equality in (II) is attained when, that is by Lemma 2.1. The distinction between the Sub- Cases (B1) and (B2) follows from the analysis of the inequality. Suppose now that. Since the inequality (II) does not provide any information on the LEV, a lower bound for the LEV is (2.6),

which is defined when and attained when. The distinction between the Sub- Cases (C11) and (C12) is obtained through analysis of the inequalities,. No informa-

tion is available when, , hence. An analysis of the preceding inequalities yields the distinction between the Sub-Cases (C21) and (C22).

The following result is about uniform bounds, which do not depend on the given information.

Corollary 2.1. (Uniform bounds for the LEV of a 3 × 3 correlation matrix). If the LEV of a 3 × 3 correlation matrix satisfies the absolute bounds. The upper bound is attained at and the lower bound at,.

Proof. Clearly, the absolute maximum of value 3 in case (A) is attained when and, which is only possible for. Similarly, the absolute minimum of value in case (B), which holds when, is attained when and, that is for .

Remark 2.2. The bounds also follow from the WS bounds in (3.1) of the next section. However, only the lower bound (B) tells us when it is attained.

3. Analytical Comparison Results

For correlation matrices the WS bounds are optimal conditionally on the value of, or equivalently on P. Since the new bounds of Theorem 2.1 depend on both P and Q, it is useful to analyze the conditions under

which the one bounds are more stringent than the others. It is remarkable that for 3 × 3 correlation matrices the WS bounds yield actually contiguous bounds for all 3 EVs ( [2] , Equation (2.31)):

(3.1)

When refereeing to the bounds in (3.1), as function of, the notation and is used for the lower respectively upper bound. Similar notations are used for the bounds in Theorem 2.1, where the upper indices refer to the various cases.

Theorem 3.1. The WS bounds compare with the bounds of Theorem 2.1 as follows:

Upper bound

(Aa)

With, one has

(Ab)

(Ac)

Lower bound

(B)

(C1)

(C2)

Proof. A case by case analysis based on Theorem 2.1 and Equation (3.1) is required. In Case (A) one has if, and only if, the inequality is fulfilled. In Sub- Case (Aa) this cannot be fulfilled, hence. Otherwise, the preceding inequality holds if, and only if, one has

.

This quadratic polynomial in has the non-negative discriminant. Therefore, the inequality holds if, with the non-negative zero of the quadratic polynomial, which is Sub-Case (Ac). The remaining situation is Sub-Case (Ab). In Case (B) the inequality holds if, and only if, one has, which is obviously fulfilled because. In Case (C1) one has if, and only if, one has

.

With Lemma 3.1 below, and the proof of Theorem 3.1, this is only possible if

,

where is the smallest zero of the preceding quadratic polynomial. Indeed, let as in Section 2, and consider the function

.

One has, and if, and only if, one has

.

The possible zeros of are. In Sub-Case (C11) one has, and only (with “?” sign) may belong to. Now, one has. One sees that and if, and only if, one has. In this situation is either a relative minimum (or an inflection point when) and a relative maximum. This implies that. If then and is a relative maximum, and again. But and

Since and one sees that. If follows that. In Sub-Case (C12) one shows similarly that. This shows the inequality. The inequality in Case (C2) is trivial. ◊

Lemma 3.1. For all one has the inequality.

Proof. If then implies that, hence, in contradiction to Lemma 2.2.

According to Theorem 3.1 the new bounds are more stringent than the WS bounds in the following cases: (Ac) and (B). Similar comparison statements can be made for other LEV bounds. For example, one can compare Theorem 2.1 with the MV bounds in [3] , Theorems 1, 2, 3, or with Theorem 2.1 in [8] . It might also be useful to

compare the new lower bounds with the classical lower bound and its improvement

in [9] , or with the lower bound in [10] , Theorem 3.1. We note that these few further possibilities do certainly not exhaust the list of LEV bounds found in the literature.

4. Some Numerical Comparisons

To conclude this study, it might be instructive to illustrate the results numerically. Since the LEV is the largest root of a cubic polynomial, a lot of formulas exist to calculate it. A most popular one is the exact trigonometric

Table 1. Numerical comparison of LEV bounds.

Vieta formula, also known under Chebyshev cube root’s formula. Following [11] in Section 6.1, one gets the roots of the depressed cubic Equation (2.2), which yield the trigonometric EV formulas:

Note that the first use of Vieta’s formulas for computing the eigenvalues of a 3 × 3 matrix is apparently due to [12] . Other authors making use of it include [13] and [14] among others.

Another quite recent and attractive evaluation of the LEV, which can be applied to correlation matrices of any dimension, is the limiting Bernoulli type ratio approximation formula in [15] , in Theorem 2.1 and Section 3. For an arbitrary correlation matrix, one has the limiting formula

.

Table 1 provides a selection of numerical examples for the possible cases in Theorem 3.1.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Marcus, M. and Minc, H. (1964) A Survey of Matrix Theory and Matrix Inequalities. Prindle, Weber & Schmidt, Boston.
[2]	Wolkowicz, H. and Styan, G.P.H. (1980) Bounds for Eigenvalues Using Traces. Linear Algebra and Its Applications, 29, 471-506. http://dx.doi.org/10.1016/0024-3795(80)90258-X
[3]	Merikoski, J.K. and Virtanen, A. (1997) Bounds for Eigenvalues Using the Trace and Determinant. Linear Algebra and Its Applications, 264, 101-108. http://dx.doi.org/10.1016/S0024-3795(97)00067-0
[4]	Merikoski, J.K. and Virtanen, A. (2001) Best Possible Bounds for Ordered Positive Numbers Using Their Sum and Product. Mathematical Inequalities & Applications, 4, 67-84. http://dx.doi.org/10.7153/mia-04-06
[5]	Zhan, X. (2006) Extremal Eigenvalues of Real Symmetric Matrices with Entries in an Interval. SIAM Journal on Matrix Analysis and Applications, 27, 851-860. http://dx.doi.org/10.1137/050627812
[6]	Hürlimann, W. (2014) Cartesian and Polar Coodinates for the n-Dimensional Elliptope. Theoretical Mathematics and Applications, 4, 1-17.
[7]	Hürlimann, W. (2015) Extreme Points of the n-Dimensional Elliptope: Application to Universal Copulas. Theoretical Mathematics and Applications. (In Press)
[8]	Huang, T.-Z. and Wang, L. (2007) Improving Bounds for Eigenvalues of Complex Matrices Using Traces. Linear Algebra and Its Applications, 426, 841-854. http://dx.doi.org/10.1016/j.laa.2007.06.008
[9]	Walker, S.G. and Van Mieghem, P. (2008) On Lower Bounds for the Largest Eigenvalue of a Symmetric Matrix. Linear Algebra and Its Applications, 429, 519-526. http://dx.doi.org/10.1016/j.laa.2008.03.007
[10]	Sharma, R., Gupta, M. and Kapoor, G. (2010) Some Better Bounds on the Variance with Applications. Journal of Mathematical Inequalities, 4, 355-363. http://dx.doi.org/10.7153/jmi-04-32
[11]	Tignol, J.-P. (2001) Galois’ Theory of Algebraic Equations. World Scientific Publishing Co., Singapore.
[12]	Smith, O.K. (1961) Eigenvalues of a Symmetric 3 × 3 Matrix. Communications ACM, 4, 168. http://dx.doi.org/10.1145/355578.366316
[13]	Kopp, J. (2008) Efficient Numerical Diagonalization of 3 × 3 Hermitian Matrices. International Journal of Modern Physics C, 19, 523-548. http://dx.doi.org/10.1142/S0129183108012303
[14]	Geoffrey, B., Benard, K. and Akanga, J. (2012) Bounds for the Second Largest Eigenvalue of Real 3 × 3 Symmetric matrices with Entries Symmetric about the Origin. Applied Mathematics, 3, 606-609. http://dx.doi.org/10.4236/am.2012.36094
[15]	Cirnu, I. (2012) Solving Polynomial Equations. Mathematica Aeterna, 2, 651-667.