1. Introduction
For the stationary Von Neumann-Landau wave equation, Chen investigated the Dirichlet problems [1] , where the generalized solution is studied by Function-analytic method. The present paper is related to the Cauchy problem: the Von Neumann-Landau wave equation
 , (1)
, (1)
where  for
for 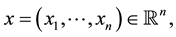
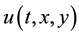 is an unknown complex valued function on
is an unknown complex valued function on  and
and  is a nonlinear complex valued function.
is a nonlinear complex valued function.
If the plus “+” is replaced by the minus “−” on right hand in Equation (1), then the resulted equation is the Schrödinger equation. For the Schrödinger equation, the well-posedness problem is investigated for various nonlinear terms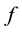 . In terms of the nonlinear terms
. In terms of the nonlinear terms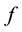 , the problem (1) can be divided into the subcritical case and the critical case for
, the problem (1) can be divided into the subcritical case and the critical case for  solutions. We are concerned with the subcritical case and obtain a local well- posedness result by the T. Kato’s method.
solutions. We are concerned with the subcritical case and obtain a local well- posedness result by the T. Kato’s method.
The paper is organized as follows. Section 2 contains the list of assumptions on the interaction term 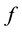 and the main result is presented. Section 3 is concerned with the Strichartz estimates. Finally, in Section 4, the main result is proved.
and the main result is presented. Section 3 is concerned with the Strichartz estimates. Finally, in Section 4, the main result is proved.
2. Statement of the Main Result
In this section we list the assumptions on the interaction term 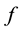 and state the main result. Firstly, we recall that the definition of admissible pair [2] .
and state the main result. Firstly, we recall that the definition of admissible pair [2] .
Definition 2.1. Fix ,
,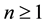 . We say that a pair
. We say that a pair 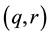 of exponents is admissible if
of exponents is admissible if
 , (2)
, (2)
and
 (3)
(3)
Remark 2.1. The pairs ![]() is always admissible, so is the
is always admissible, so is the ![]() if
if ![]() The two pairs are called the endpoint cases.
The two pairs are called the endpoint cases.
Secondly, let ![]() satisfy
satisfy
![]() , (4)
, (4)
and
![]() , (5)
, (5)
for all ![]() such that
such that ![]() with
with
![]() (6)
(6)
where ![]() is a constant independent of
is a constant independent of ![]() Set
Set
![]() , (7)
, (7)
for all measurable function ![]() and a.e.
and a.e.![]() .
.
Finally, let us make the notion of solution more precise.
Definition 2.2. Let ![]() be an interval such that
be an interval such that ![]() We say that
We say that ![]() is a strong
is a strong ![]() -solution of (1) on
-solution of (1) on ![]() if
if ![]() satisfies the integral equation
satisfies the integral equation
![]() , (8)
, (8)
for all ![]() where
where ![]()
The main result is the following theorem:
Theorem 1. Suppose ![]() Let
Let ![]() satisfy (4)-(6). If
satisfy (4)-(6). If ![]() (considered as a function
(considered as a function![]() ) is of class
) is of class![]() , then the Cauchy problem (1) is locally well posed in
, then the Cauchy problem (1) is locally well posed in ![]() More specially, the following properties hold:
More specially, the following properties hold:
(i) For any ![]() there exists a time
there exists a time ![]() and constant
and constant ![]() such that for each
such that for each ![]() in the ball
in the ball ![]() there exists a unique strong
there exists a unique strong ![]() -solution
-solution ![]() to the Equation (1) in
to the Equation (1) in ![]() such that
such that
![]() (9)
(9)
where ![]() and
and ![]() is an admissible pair.
is an admissible pair.
(ii) The map ![]() is continuous from
is continuous from ![]() to
to ![]()
(iii) For every ![]() the unique solution
the unique solution ![]() is defined on a maximal interval
is defined on a maximal interval ![]() with
with ![]() and
and ![]()
(iv) There is the blowup alternative: If ![]() then
then ![]() as
as ![]() (respectively, if
(respectively, if ![]() then
then ![]() as
as![]() ).
).
Remark 2.2. It follows from Strichartz estimates that
![]() ,
,
for any admissible pair ![]()
Remark 2.3. For the Schrödinger equations, the similar results hold [2] . It implies a fact that the ellipticity of the operator ![]() is not the key point in the local well-posedness problem.
is not the key point in the local well-posedness problem.
3. Strichartz Estimates
In this subsection, we recall that the Strichartz estimates. Let ![]() denote a general Fourier variable in
denote a general Fourier variable in ![]()
![]()
![]() Let
Let ![]() then by Fourier transform(denoting by
then by Fourier transform(denoting by ![]() or
or![]() ) we have
) we have
![]() , (10)
, (10)
for any ![]() It is easy to verify that the
It is easy to verify that the ![]() is a self-adjoint unbounded operator on
is a self-adjoint unbounded operator on ![]() with the domain
with the domain ![]() Then, by Stone theorem we see that
Then, by Stone theorem we see that ![]() is an unitary group on
is an unitary group on![]() . Moreover,
. Moreover,
![]() can be expressed explicitly by Fourier transform.
can be expressed explicitly by Fourier transform.
![]() , (11)
, (11)
for any ![]() By the direct compute, we conclude
By the direct compute, we conclude
![]() (12)
(12)
The following result is the fundamental estimate for ![]()
Lemma 1. If ![]() and
and ![]() then
then ![]() maps
maps ![]() continuously to
continuously to ![]() and
and
![]() (13)
(13)
where ![]() is the dual exponent of
is the dual exponent of ![]() defined by the formula
defined by the formula ![]()
Proof. For the proof please see [3] or [4] . □
The following estimates, known as Strichartz estimates, are key points in the method introduced by T. Kato [5] .
Lemma 2. Let ![]() and
and ![]() be any admissible exponents. Then, we have the homogeneous Strichartz estimate
be any admissible exponents. Then, we have the homogeneous Strichartz estimate
![]() (14)
(14)
the dual homogeneous Strichartz estimate
![]() (15)
(15)
and the inhomogeneous Strichartz estimate
![]() , (16)
, (16)
for any interval ![]() and real number
and real number ![]()
Proof. For the proof please see [3] or [4] in the non-endpoint case. On the other hand, the proof in the endpoint case follows from the theorem 1.2 in [6] and the lemma 1 in the present paper. □
4. The Proof of Theorem
Proof. Let ![]() be such that
be such that ![]() for
for ![]() and
and ![]() for
for ![]() Setting
Setting
![]()
one easily verifies that for any ![]()
![]() (17)
(17)
Set ![]() for
for ![]() Using (17), we deduce from Hölder’s inequality that
Using (17), we deduce from Hölder’s inequality that
![]() (18)
(18)
And it follows from Remark 1.3.1 (vii) in [2] that
![]() (19)
(19)
We now proceed in four steps.
Step 1. Proof of (i). Fix ![]() to be chosen later, and let
to be chosen later, and let![]() ,
, ![]() be such that
be such that ![]() is an ad- missible pair, and set
is an ad- missible pair, and set ![]() Consider the set
Consider the set
![]() , (20)
, (20)
equipped with the distance
![]() (21)
(21)
We claim that ![]() is a complete metric space. Indeed, let
is a complete metric space. Indeed, let ![]() be a Cauchy sequence. Clearly,
be a Cauchy sequence. Clearly, ![]() is also a Cauchy sequence in
is also a Cauchy sequence in ![]() and
and ![]() In particular, there exists a function
In particular, there exists a function ![]() such that
such that ![]() in
in ![]() and
and ![]() as
as
![]() Applying theorem 1.2.5 in [2] twice, we conclude that
Applying theorem 1.2.5 in [2] twice, we conclude that
![]() ,
,
and that
![]()
thus, ![]() in
in ![]() as
as ![]()
Taking up any ![]() Since
Since ![]() is continuous
is continuous ![]() it follows that
it follows that ![]() is measurable, and we deduce easily that
is measurable, and we deduce easily that ![]() Similarly, since
Similarly, since ![]() is continuous
is continuous ![]() we see that
we see that ![]() Using inequalities (18) and (19) and Remark
Using inequalities (18) and (19) and Remark
1.2.2 (iii) in [2] , We deduce the following:
![]()
![]()
and
![]()
Using the embedding ![]() and Hölder’s inequality in time, we deduce from the above estimates that
and Hölder’s inequality in time, we deduce from the above estimates that
![]() , (22)
, (22)
and
![]() (23)
(23)
Given![]() . For any
. For any ![]() let
let ![]() be defined by
be defined by
![]() (24)
(24)
It follows from (22) and Strichartz estimates (lemma 2) that
![]() (25)
(25)
and
![]() (26)
(26)
Also, we deduce from (23) that
![]() (27)
(27)
Finally, note that ![]() We now proceed as follows. For any
We now proceed as follows. For any ![]() we set
we set ![]() and we let
and we let ![]() be the unique positive number so that
be the unique positive number so that
![]() (28)
(28)
It then follows from (26) and (28) that for any ![]()
![]() (29)
(29)
Thus, ![]() and by (27) we obtain
and by (27) we obtain
![]() (30)
(30)
In particular, ![]() is a strict contraction on
is a strict contraction on ![]() By Banach’s fixed-point theorem,
By Banach’s fixed-point theorem, ![]() has a unique fixed
has a unique fixed
point ![]() that is
that is ![]() satisfies (8). By (25),
satisfies (8). By (25),![]() . By the definition 2.2, we con- clude that
. By the definition 2.2, we con- clude that ![]() is a strong
is a strong ![]() -solution of (1) on
-solution of (1) on ![]() Note that
Note that ![]() is decreasing on
is decreasing on![]() , then the estimate (9) holds for
, then the estimate (9) holds for ![]() by letting
by letting ![]() in (29).
in (29).
For uniqueness, assume that ![]() are two strong
are two strong ![]() -solution of (1) on
-solution of (1) on ![]() with the same initial value
with the same initial value![]() . Then, we have
. Then, we have
![]() (31)
(31)
For simplicity, we set
![]() ,
,
for ![]() and
and ![]() For any interval
For any interval ![]() by (18) and Strichartz estimates (16), then we obtain
by (18) and Strichartz estimates (16), then we obtain
![]() (32)
(32)
Similarly, for ![]() we have
we have
![]() (33)
(33)
Note that ![]() Then, it follows from that
Then, it follows from that
![]() , (34)
, (34)
where the constant ![]() and the constant
and the constant ![]() is independent of
is independent of ![]() by above inequalities. Note that
by above inequalities. Note that ![]() we conclude that
we conclude that ![]() by the lemma 4.2.2 in [2] . So
by the lemma 4.2.2 in [2] . So ![]()
Step 2. Proof of (ii). Suppose that ![]() in
in ![]() as
as ![]() By the part (i), we denote
By the part (i), we denote ![]() and
and ![]() by
by
the unique solution of (1) corresponding to the initial value ![]() and
and![]() , respectively. We will show that
, respectively. We will show that ![]() in
in ![]() as
as ![]() Note that
Note that
![]() (35)
(35)
and the estimate (29) which implies that (27) holds for ![]() Note that the choosing of the time
Note that the choosing of the time ![]() in (28), it follows from (27) with (30) that
in (28), it follows from (27) with (30) that
![]() (36)
(36)
Hence, we have
![]() (37)
(37)
Next, we need to estimate ![]() Note that
Note that ![]() commutes with
commutes with![]() , and so
, and so
![]() (38)
(38)
A similar identity holds for ![]() We use the assumption
We use the assumption ![]() which implies that
which implies that ![]() where
where ![]() is a
is a ![]() real matrix. Therefore, we may write
real matrix. Therefore, we may write
![]() (39)
(39)
Note that ![]() and
and ![]() are also
are also ![]() so that
so that ![]() and from (17) we deduce that
and from (17) we deduce that ![]() and
and ![]() for any
for any ![]() and some constant
and some constant ![]() Therefore, arguing as in Step 1, we obtain the estimate
Therefore, arguing as in Step 1, we obtain the estimate
![]() (40)
(40)
By choosing ![]() as (28) and noting that
as (28) and noting that ![]() from (40) we obtain that
from (40) we obtain that
![]() (41)
(41)
There, if we prove that
![]() , (42)
, (42)
as ![]() then we have
then we have
![]() , (43)
, (43)
as ![]() which, combined with (37), yields the desired convergence. we prove (42) by contradiction, and we assume that there exists
which, combined with (37), yields the desired convergence. we prove (42) by contradiction, and we assume that there exists ![]() and a subsequence, which we still denote by
and a subsequence, which we still denote by ![]() such that
such that
![]() (44)
(44)
By using (37) and possibly extracting a subsequence, we may assume that ![]() a.e. on
a.e. on ![]() and that there exists
and that there exists ![]() such that
such that ![]() a.e. on
a.e. on ![]() In particular, both
In particular, both ![]() and
and ![]() converge to 0 a.e. on
converge to 0 a.e. on ![]() Since
Since
![]()
and
![]()
we obtain from the dominated convergence a contradiction with (44).
Step 3. Proof of (iii). Consider ![]() and let
and let
![]()
![]()
It follows from part (i) there exists a solution
![]() ,
,
of (1).
Step 4. Proof of (iv). Suppose now that ![]() and assume that there exist
and assume that there exist ![]() and a sequence
and a sequence ![]() such that
such that ![]() Let
Let ![]() be such that
be such that ![]() By part (i), from the initial data
By part (i), from the initial data ![]() one can extend
one can extend ![]() up to
up to![]() , which contradicts maximality. Therefore,
, which contradicts maximality. Therefore,
![]()
One shows by the same argument that if ![]() then
then
![]()
This completes the proof. □
Acknowledegments
We are grateful to the anonymous referee for many helpful comments and suggestions, which have been incorporated into this version of the paper. C. Liu was supported in part by the NSFC under Grants No. 11101171, 11071095 and the Fundamental Research Funds for the Central Universities. And M. Liu was supported by science research foundation of Wuhan Institute of Technology under grants No. k201422.